Электрическое поле постоянных токов, основные характеристики и уравнения

1.

Краткое содержание
1. Электрическое поле постоянных токов,
основные характеристики и уравнения,
формальная аналогия уравнений
электростационарного и
электростатического поля
2. Граничные условия
3. Методы изображений

2.

Мерой направленного движения электрических зарядов в
проводниках служит вектор плотности тока проводимости:
J lim
q v
n n
n
V 0
V
qn - электрический заряд частицы n, движущейся со скоростью vn
, V - объем, в пределах которого производится суммирование.
Поток вектора плотности тока проводимости - ток
проводимости
i J ds
S
Плотность тока проводимости и напряженность электрического поля
связаны по закону Ома через среднюю проводимость среды:
J E
(закон Ома в дифференциальной форме). В диэлектрике,
окружающем проводник с током, так и внутри самих проводников,
будут существовать электрическое и магнитное поле постоянного
тока, называемые стационарными.
2

3.

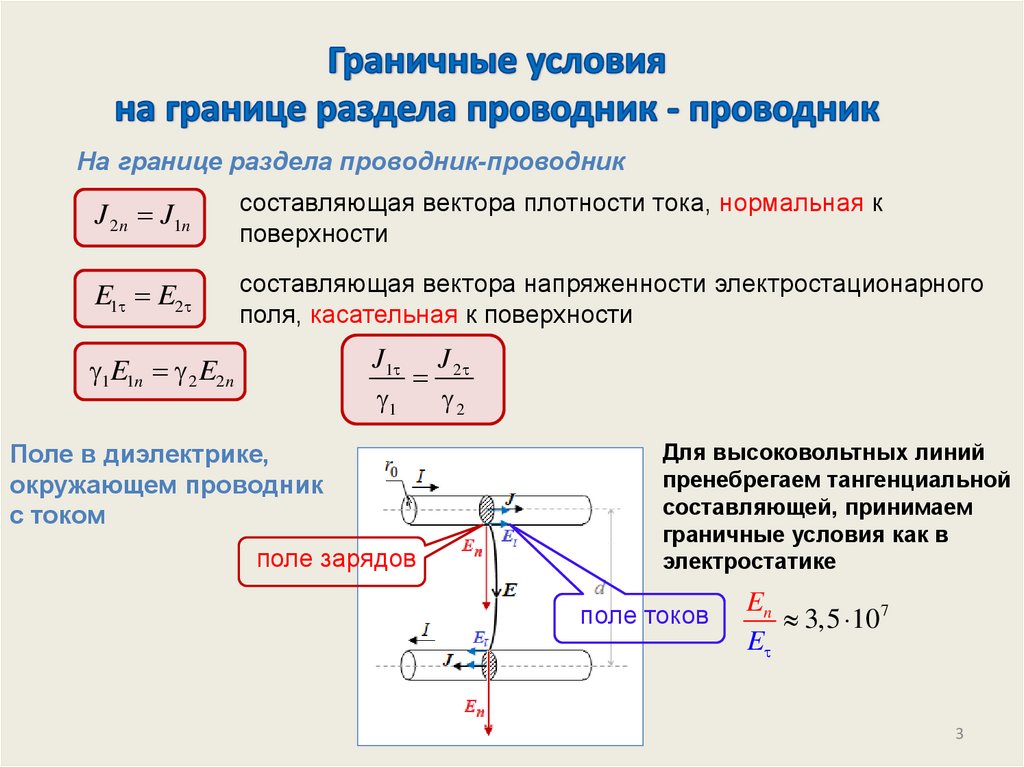
На границе раздела проводник-проводник
J 2 n J1n
составляющая вектора плотности тока, нормальная к
поверхности
E1 E2
составляющая вектора напряженности электростационарного
поля, касательная к поверхности
J 1 J 2
1
2
1E1n 2 E2 n
Поле в диэлектрике,
окружающем проводник
с током
поле зарядов
Для высоковольтных линий
пренебрегаем тангенциальной
составляющей, принимаем
граничные условия как в
электростатике
поле токов
En
3,5 107
E
3

4.

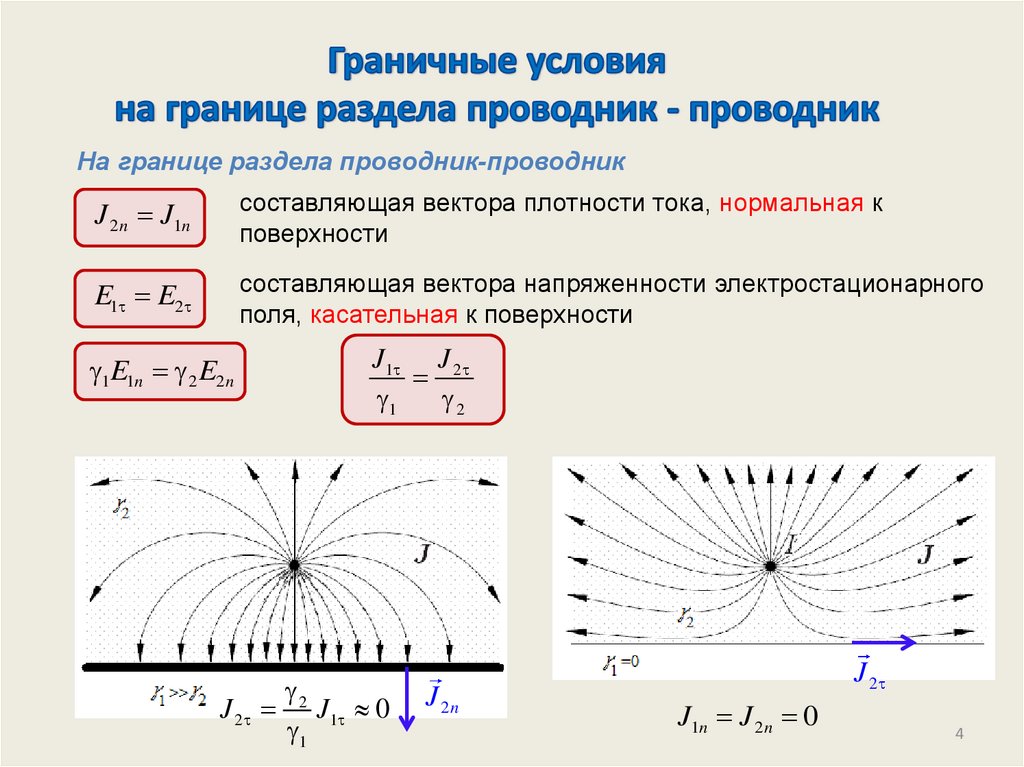
На границе раздела проводник-проводник
J 2 n J1n
составляющая вектора плотности тока, нормальная к
поверхности
E1 E2
составляющая вектора напряженности электростационарного
поля, касательная к поверхности
1E1n 2 E2 n
J 1 J 2
1
2
J 2 2 J 1 0
1
J 2n
J 2
J1n J 2 n 0
4

5.

Метод формальной аналогии позволяет при расчете токов в
проводящей среде воспользоваться известными решениями
соответствующих электростатических задач (или наоборот). Так
линейная плотность заряда соответствует току утечки на
единицу длины I 0 .
Проводимость G между двумя электродами в проводящей среде при
одинаковой геометрии определяется через емкость С между теми
же электродами в диэлектрике (или наоборот), при наличии
аналогии полей выполняется соотношение
C r 0
G
Так выражения для емкости и проводимости между жилой и
оболочкой в случае неидеальной изоляции коаксиального кабеля
2
имеют вид:
2 r 0
G
См/м
0
C0
Ф/м
R
2
R2
ln
ln
R1
R1
5

6.

Плоский конденсатор с двумя слоями толщиной d1 = d2=1 см;
10
несовершенная изоляция 1 слоя r1 2 , 1 2 10 См/см и несовершенная
изоляция 2 слоя r 2 4 , 2 10 10 См/см подключили к источнику U = 3 кВ.
Найти напряженность поля в каждом слое, удельное сопротивление
изоляции конденсатора, мощность, выделяющуюся в единице объема
изоляции, своб и связ на границе слоев изоляции.
y
Напряжение между пластинами конденсатора
J
(разность потенциалов):
ε2
ε1
n
x
U
d1 d 2
E ( x)dx E1d1 E2d 2
J1 x d J 2 x d
0
1
2
d1
d2
J1 J 2
n dx
1
1E1 2 E2
3000 0,01E1 0,01E2
2E1 1E2
E1 1 кВ/см
E1 105 В/м
E2 2 105 В/м
En Ex E
J1 J 2 =2 10 10 E1 0,2 10 6 A/cм 2
Jn J x J
D1n D1 r1 0 E1 2 103 0 Кл/см 2
J dx
E dx
1
D2 n D2 r 2 0 E2 8 103 0 Кл/см 2
E2 2 кВ/см
0 Ф/см
6

7.

P1n P1 ( r1 1) 0 E1 103 0 Кл/см 2
P2 n P2 ( r 2 1) 0 E2 6 10 0 Кл/см
3
0 Ф/см
2
своб D2 D1 6 103 0 Кл/см2
y
ε1
J
ε2
Активная мощность в единице объема:
n
x
1
2
d1
d2
связ P1 P2 5 103 0 Кл/см2
p2 2 E22 0,4 мВт/см3
p1 1E12 0,2 мВт/см3
J1 J 2 Удельное сопротивление изоляции:
n dx
En Ex E
R0
U
3000
2
0,2
Ом/см
J 0,2 10 6
Замечание: Если бы изоляция была совершенная, то
граничные условия D1 x d D2 x d
1
Jn J x J
U E1d1 E2d2
E1 2 кВ/см
J dx
E dx
r1 0 E1 r 2 0 E2
E2 1 кВ/см
1
7

8.

Дано: Изоляция коаксиального кабеля имеет удельную проводимость
10 9 См/м . Радиус жилы R1 0,4 cм , оболочки R2 0,8 cм.
Напряжение между жилой и оболочкой U 600 В . Определить удельную
проводимость кабеля, плотность тока утечки на поверхности жилы и
оболочки, удельную мощность в тех же точках, активную мощность в
изоляции кабеля на единицу длины.
Решение: Выберем в качестве поверхности через
которую будем рассчитывать ток утечки с поверхности
жилы цилиндр, ось которого совпадает с осью жилы,
радиусом r и длиной . Поток вектора плотности тока
через боковую поверхность определит весь ток утечки
(по торцевым поверхностям поток не проходит).
I ут
Ток утечки
Jds JS
бок
J 2 r
Sцил
J (r )
I ут
2 r
I0
2 r
модуль!
I 0 - ток утечки на единицу длины [А/м]
8

9.

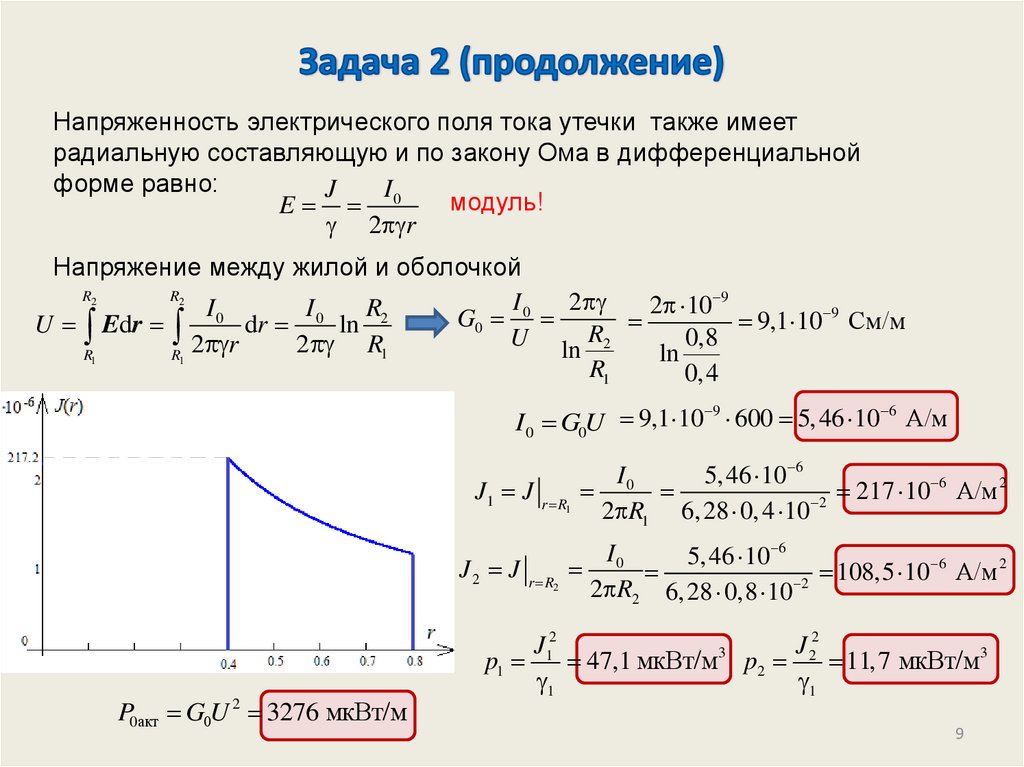
Напряженность электрического поля тока утечки также имеет
радиальную составляющую и по закону Ома в дифференциальной
форме равно:
I
J
модуль!
E 0
2 r
Напряжение между жилой и оболочкой
R2
R2
9
I0
2
2
10
I0
I0
R2
9
G0
9,1
10
См/м
U Edr
dr
ln
R
0,8
U
2
2 r
2 R1
ln
R1
R1
ln
R1
0, 4
9
6
I 0 G0U 9,1 10 600 5, 46 10 А/м
J1 J
J2 J
P0акт G0U 2 3276 мкВт/м
r R1
r R2
5, 46 10 6
I0
6
2
217
10
А/м
2 R1 6, 28 0, 4 10 2
I0
5, 46 10 6
6
2
108,5
10
А/м
2 R2 6, 28 0,8 10 2
J12
J 22
3
p1
47,1 мкВт/м p2
11,7 мкВт/м3
1
1
9

10.

Дано: Определить ток утечки и сопротивление изоляции двухслойного
цилиндрического конденсатора на 1 м длины, если U = 100 В, R0 = 5 мм,
R1 =20 мм, R2 = 40 мм, удельная проводимость неидеальной изоляции
7
первого слоя 1 10 7 См/м , второго слоя 2 2 10 См/м .
Решение: Выберем в качестве поверхности через
которую будем рассчитывать ток утечки с поверхности
жилы цилиндр, ось которого совпадает с осью жилы,
радиусом r и длиной . Поток вектора плотности тока
через боковую поверхность определит весь ток утечки
(по торцевым поверхностям поток не проходит).
E Er
Ток утечки
I ут
Jds JS
бок
J 2 r
R0 r R2
Sцил
I ут
I0
I 0 - ток утечки на единицу длины [А/м]
2 r
2 r
I 1
J (r )
1) в первом слое R0 r R1 E1 (r )
0
1
2 1 r
J (r )
2) во втором слое R1 r R2 E2 (r )
I 1
J (r )
0
2
2 2 r
10

11.

Напряжение между жилой и оболочкой
2
I0 1
I 1
I 1 R
1 R
U E1dr E2dr
dr 0
dr 0 ln 1 ln 2
2 1 r
2 2 r
2 1 R0 2 R1
R0
R1
R0
R1
R1
R2
R1
E Er
R
Удельная проводимость двухслойного конденсатора
с несовершенной изоляцией
I
2
G0 0
U 1 R1 1 R2
ln ln
1 R0 2 R1
2
G0
3,624 10 7 См/м
20
1
40
1
ln
ln
7
5 2 10 7 20
10
Удельное сопротивление изоляции двухслойного цилиндрического конденсатора
U
1
1
6
2,76
10
Ом/м
7
I 0 G0 3,624 10
U
7
6
I
Ток утечки на единицу длины 0 R G0U 3,624 10 100 36, 24 10 А/м
0
R0
11

12.

Для осуществления соединения какой-либо точки электрической
цепи (электроустановки) с землей используют заземлитель металлический электрод или систему электродов. Методами
теории поля определяются сопротивления при растекании тока
по земле с поверхностей погруженных в нее электродов,
называемые сопротивления заземления. При наличии
неоднородности среды (почвы) используют методы
изображений.
Важнейшим является расчет шагового напряжения - разности
потенциалов на поверхности земли на расстоянии, равном
ширине шага. Рассчитывается радиус "безопасной зоны",
шаговое напряжение вне этой зоны не превышает предельно
допустимого значения. В соответствии с граничными условиями
на поверхности почвы есть только тангенциальная
составляющая плотности тока, так как в воздухе J n 0 .
Тангенциальная составляющая плотности тока определяет
наличие на поверхности тангенциальной составляющей
напряженности электрического поля и разности потенциалов на
поверхности земли.
12

13.

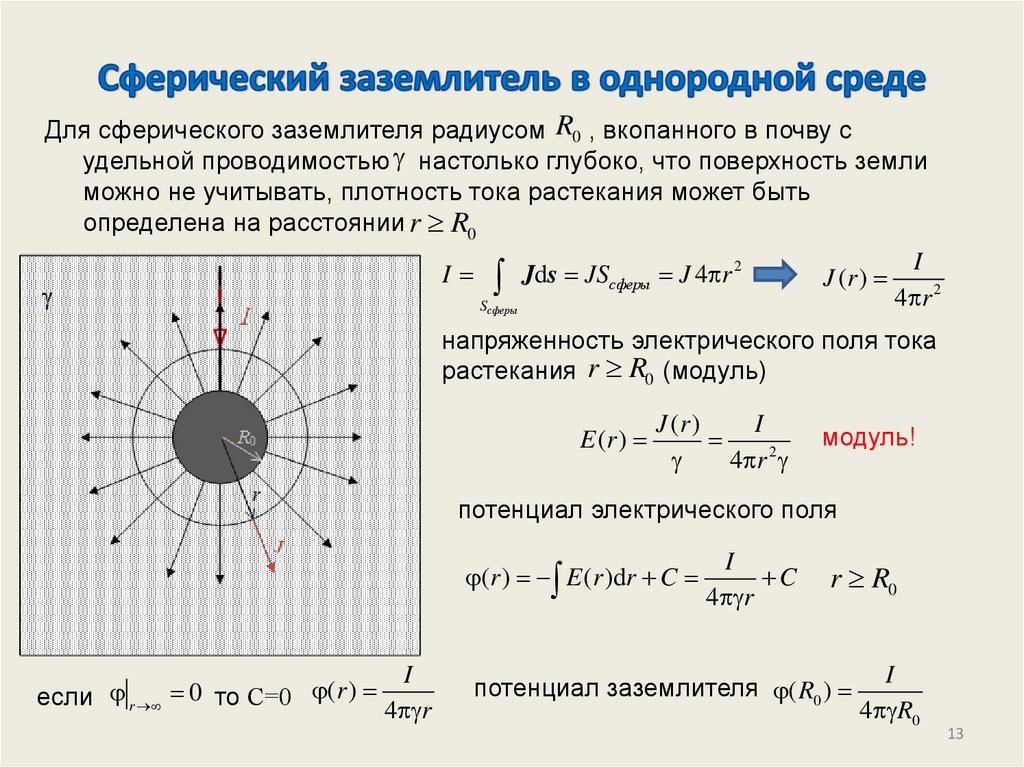
Для сферического заземлителя радиусом R0 , вкопанного в почву с
удельной проводимостью настолько глубоко, что поверхность земли
можно не учитывать, плотность тока растекания может быть
определена на расстоянии r R0
I
Jds JSсферы J 4 r 2
J (r )
Sсферы
I
4 r 2
напряженность электрического поля тока
растекания r R0 (модуль)
E (r )
J (r )
I
4 r 2
модуль!
потенциал электрического поля
(r ) E (r )dr C
если r 0 то С=0 (r )
I
4 r
I
C
4 r
r R0
потенциал заземлителя ( R0 )
I
4 R0
13

14.

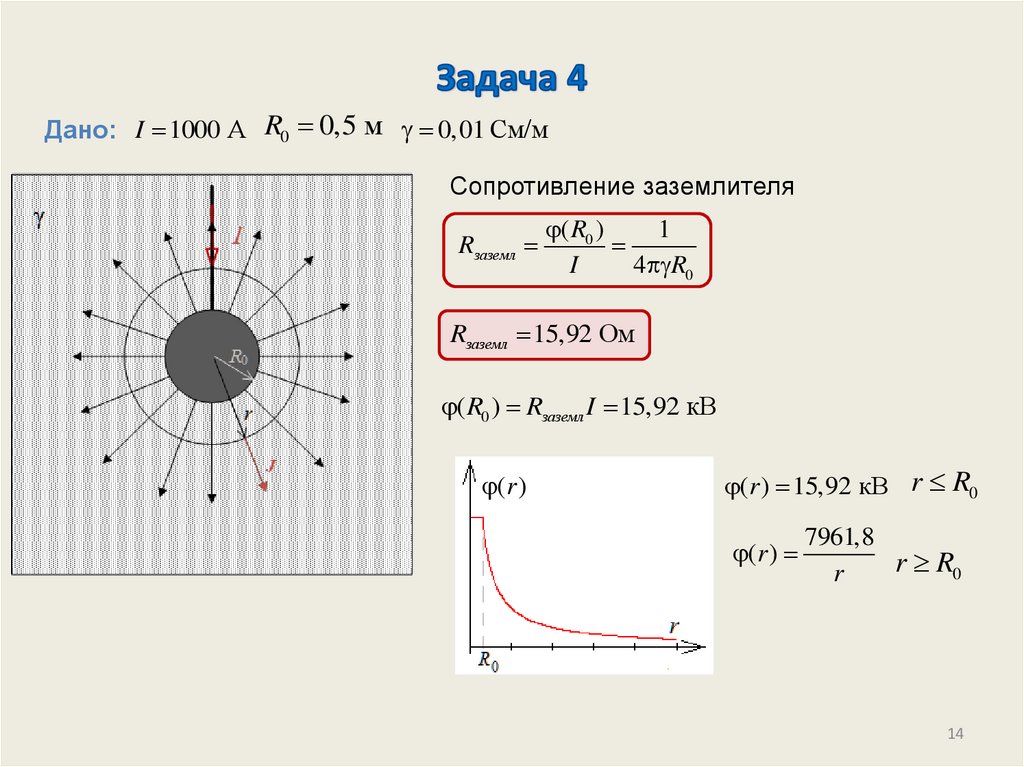
Дано: I 1000 А R0 0,5 м 0,01 См/м
Сопротивление заземлителя
Rзаземл
( R0 )
1
I
4 R0
Rзаземл 15,92 Ом
( R0 ) Rзаземл I 15,92 кВ
(r )
(r ) 15,92 кВ r R0
(r )
7961,8
r R0
r
14

15.

Рассмотрим задачу расчета электростационарного поля полусферического
заземлителя радиуса R0 , расположенного в почве с удельной
проводимостью 1 . Неоднородная среда 2 0 , J 2 n J1n 0 .
На поверхности есть только J1 .
J1
J1
область решения
Поле полусферического заземлителя совпадает с полем сферического
заземлителя в однородной среде с током 2I (в нижней полуплоскости)
15

16.

Дано: Полусферический заземлитель R0 0,5 м расположен в почве
0,01 См/м . Определить сопротивление заземлителя относительно
«бесконечно» удаленной точки (сопротивление растекания). Полагая,
что через заземлитель произошло замыкание с U 35 кВ найти ток
короткого замыкания, шаговое напряжение на расстоянии 20 м от
заземлителя, радиус безопасной зоны, в которой шаговое напряжение
не превышает 12 В. Длина шага lш 0,7 м
2 I JSсферы J 4 r 2
35 кВ
lш
x
J (r )
2I
I
4 r 2 2 r 2
E (r )
J (r )
I
1
2 r 2 1
r R0
область решения
I
потенциал электрического поля (r )
C r 0
2 r
(r )
I
2 r
16

17.

Сопротивление полусферического заземлителя
Rзаземл
( R0 )
1
I
2 R0
Rзаземл 31,85 Ом
Ток короткого замыкания
I
( R0 )
U
1100 A
Rзаземл Rзаземл
Шаговое напряжение U ш ( x) ( x) ( x lш )
x lш
E (r )dr
x
U ш ( x) ( x) ( x lш )
I lш
I
I
I 1
1
2 x 2 ( x lш ) 2 x x lш 2 x ( x lш )
Если x 20 м lш 0,7 м
U ш ( x) x 20
1100 0,7
29,6 B
2 0,01 20 (20 0,7)
Радиус безопасной зоны U ш ( x) xб 12 B
xб 32 м
17

18.

Расчет поля в неоднородной среде проводится с помощью метода
изображений (задача Сирла)
область решения
Шаговое напряжение с учетом тока двух заземлителей
2 I
1
1
I
1
1
U ш ( x)
2
2
2
2
2
2
2
2
4 1 x h
2
( x lш ) h
( x lш ) h
1
x h
18

19.

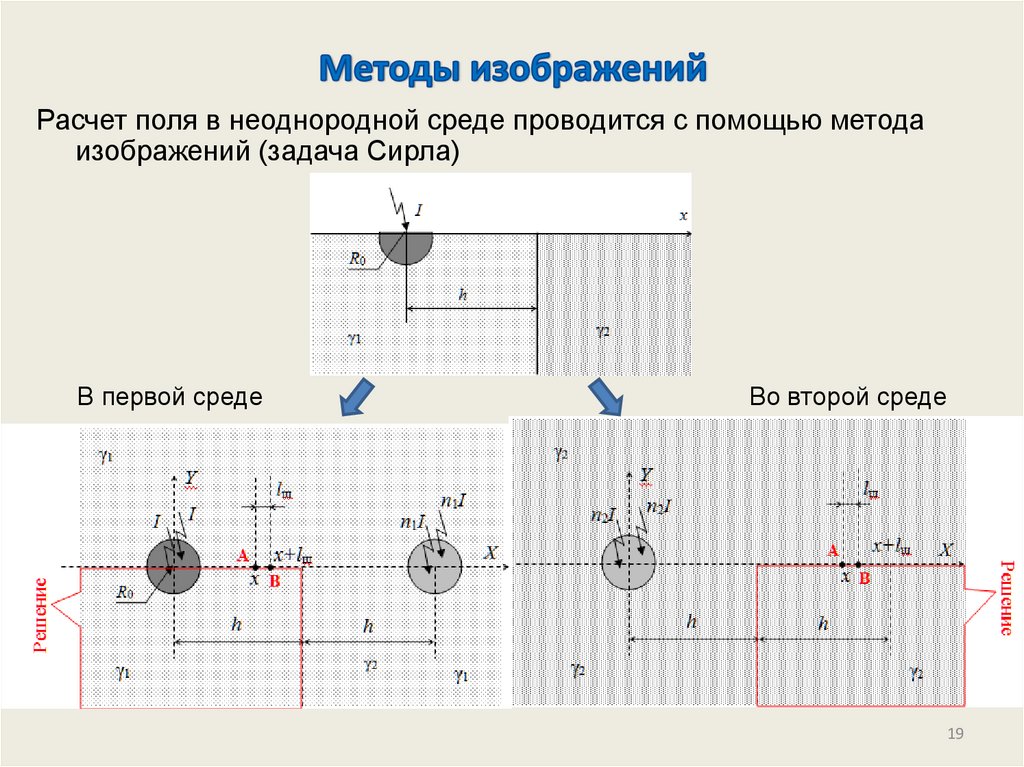
Расчет поля в неоднородной среде проводится с помощью метода
изображений (задача Сирла)
В первой среде
Во второй среде
19

20.

Автор доц. каф. ТОЭ НИУ «МЭИ»
Жохова М.П.
[email protected]
20