Похожие презентации:
Вычисление площадей плоских фигур. Вычисление объема тела вращения. Несобственный интеграл. Лекция 13
1.
Лекция 13Вычисление площадей плоских фигур
Вычисление длины дуги плоской кривой
Вычисление объема тела вращения
Несобственный интеграл.
Несобственный интеграл I рода.
Несобственный интеграл II рода.
1
2.
Вычисление площадей плоских фигурПо геометрическому смыслу определенного
интеграла, площадь криволинейной
трапеции, расположенной выше оси ОХ
равна соответствующему определенному
интегралу :
f (x) 0
y
S
0
a
b
a
b
x
b
S f ( x )dx (1)
a
Если криволинейная трапеция
расположена ниже оси ОХ, то ее площадь
может быть найдена по формуле:
y
0
x
S
b
f (x) 0
S f ( x )dx (2)
a
Формулы (1) и (2) можно объединить в
одну для случая, когда функция f(x)
сохраняет знак на [a; b]
b
S f ( x )dx
a
2
3.
Площадь фигуры, ограниченнойкривыми y = f1(x) и y = f2(x), прямыми
x = a, x = b при условии f2 ( x ) f1( x )
находится по формуле:
b
y
f2(x)
S
0
a
S f2 ( x ) f1( x ) dx
x
b
f1(x)
a
y
Если плоская фигура имеет «сложную»
форму, то прямыми, параллельными оси OY,
ее следует разбить на части так, чтобы можно
было применить известные формулы.
S3
S1
S2
S
4
0 a
bx
Если криволинейная трапеция ограничена кривой, заданной
параметрически, прямыми x = a, x = b и осью OX:
x x(t );
t ;
y y (t ).
S y (t ) x (t ) dt
3
4.
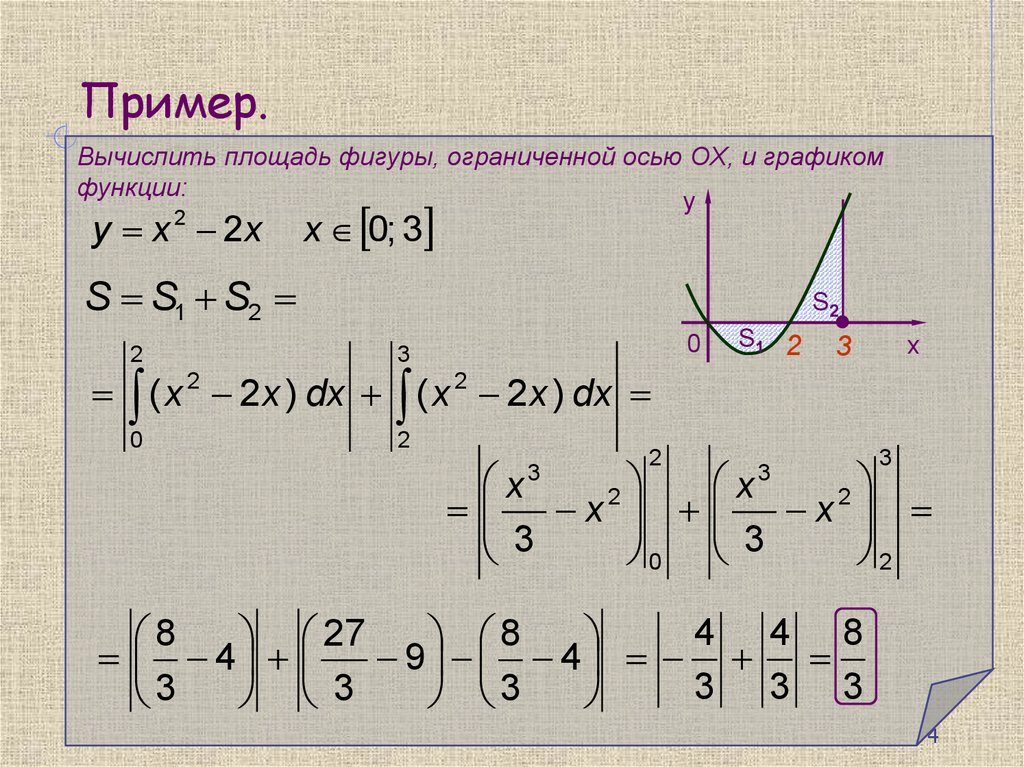
Пример.Вычислить площадь фигуры, ограниченной осью OX, и графиком
функции:
y
y x 2 2x
x 0; 3
S S1 S2
S2
2
3
0
2
0
S1 2
3
x
( x 2 2 x ) dx ( x 2 2 x ) dx
2
3
x
x
2
2
x
x
3
0 3
2
3
3
4 4 8
8
27
8
4
9 4
3 3 3
3
3
3
4
5.
Вычисление длины дуги плоскойкривой
b
L 1 y 2 dx
a
Если уравнение кривой AB задано в параметрической форме:
x x(t );
t ;
y y (t ).
x( ) a;
то длина дуги кривой находится по
формуле:
x( ) b.
L x 2 y 2 dt
Если кривая AB задана в полярных координатах:
r r ( )
.
то длина дуги кривой находится по
формуле:
L r 2 r 2 d
5
6.
Пример.Вычислить длину дуги окружности, заданной уравнением: x
от точки А(2;
2 cos t;
y 2 sin t .
0) до точки B(1; 3 )
Найдем как изменяется параметр t при
переходе от точки А к точке В:
y
В
А
2
0
2 2 cos t ;
t 0
0 2 sin t .
x
1 2 cos t ;
t
3
3 2 sin t .
3
3
2
2
L (2 cos t ) 2 (2 sin t ) 2 dt 4 sin t 4 cos t dt
0
3
2dt 2t
0
3
0
2
3
0
6
7.
Вычисление объема тела вращенияПусть вокруг оси OX вращается криволинейная трапеция,
ограниченная непрерывной линией y = f(x) > 0, отрезком [a; b] и
прямыми x = a, x = b.
. при вращении фигура
Полученная
y
называется телом вращения.
Объем полученного тела
вычисляется по формуле:
b
0
а
b
x
Vx y 2dx
a
Если криволинейная трапеция, ограниченная
графиком функции x = q(y) > 0, прямыми y = c,
y = d и осью OY, то объем тела, образованного
вращением этой фигуры вокруг оси OY равен:
d
Vy x 2dy
c
7
8.
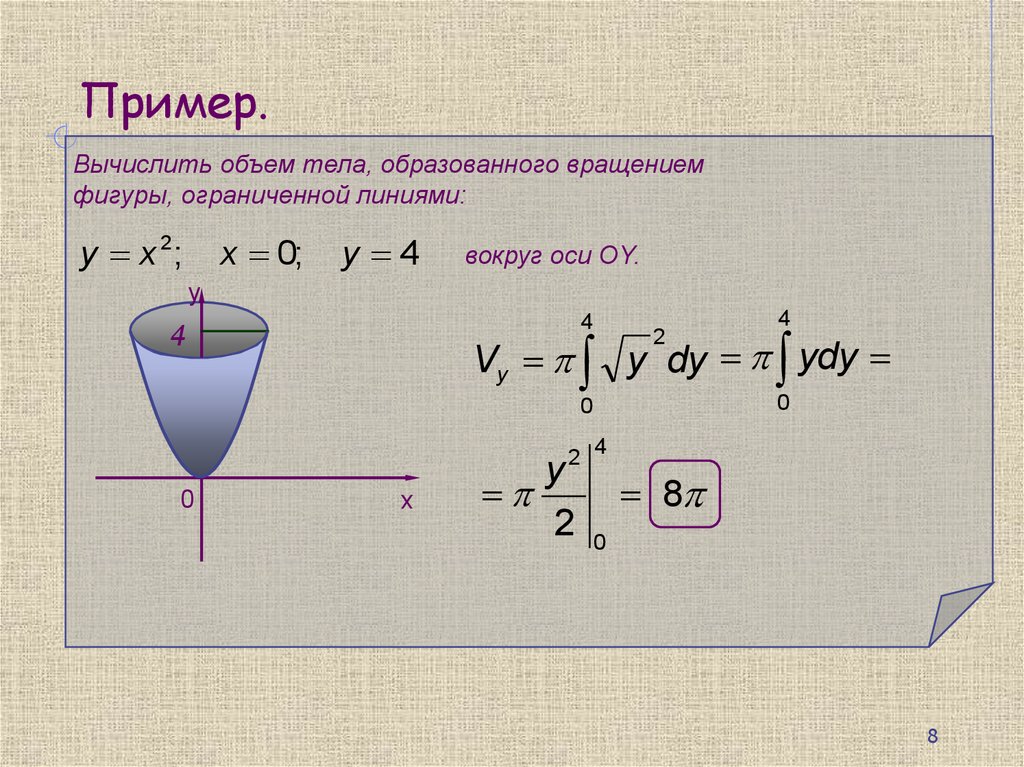
Пример.Вычислить объем тела, образованного вращением
фигуры, ограниченной линиями:
y x 2;
x 0;
y 4
вокруг оси OY.
y
4
4
0
0
2
0
4
Vy y dy ydy
2
x
y
2
4
8
0
8
9.
910.
Несобственныйb интегралОпределенный интеграл
f ( x )dx где промежуток интегрирования
a
[a; b] конечный, а подынтегральная функция f(x) непрерывна на
отрезке [a; b], называют еще собственным интегралом.
Так называемые несобственные интегралы бывают двух видов:
Определенный интеграл от непрерывной функции, но с
бесконечным промежутком интегрирования (несобственный
интеграл 1 рода)
Определенный интеграл с конечным промежутком
интегрирования, но от функции, имеющей на нем
бесконечный разрыв (несобственный интеграл 2 рода)
10
11.
Несобственный интеграл 1 родаПусть функция f(x) непрерывна на промежутке
[a; )
b
lim f ( x )dx
Если существует конечный предел
b
a
то его называют несобственным интегралом первого рода и
обозначают:
f ( x )dx
a
b
lim f ( x )dx
b
a
В этом случае говорят, что несобственный интеграл сходится.
Если указанный предел не существует или он бесконечен, то
говорят, что несобственный интеграл расходится.
Аналогично определяется несобственный интеграл на промежутке
( ; b ]
b
f ( x )dx
b
lim f ( x )dx
a
a
11
12.
Несобственный интеграл с двумя бесконечными пределамиопределяется формулой:
c
c
f ( x )dx f ( x )dx f ( x )dx
В этом случае интеграл слева сходится лишь тогда, когда сходятся
оба интеграла справа.
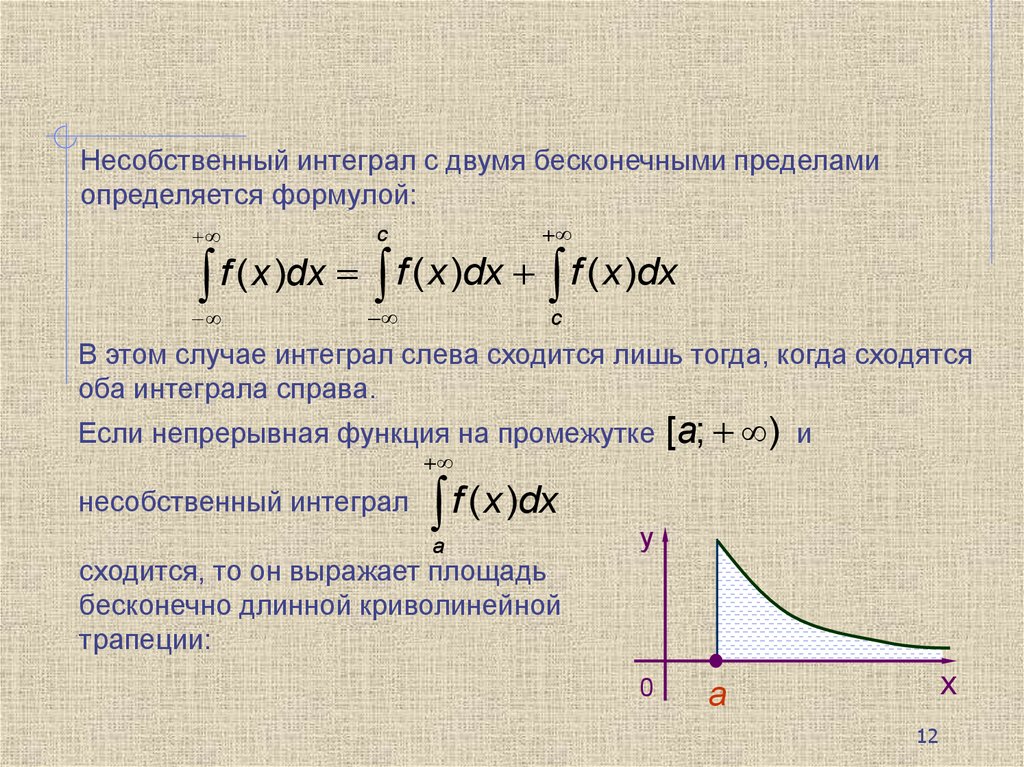
Если непрерывная функция на промежутке
несобственный интеграл
f ( x )dx
a
[a; )
и
y
сходится, то он выражает площадь
бесконечно длинной криволинейной
трапеции:
0
x
a
12
13.
Примеры.Вычислить несобственные интегралы или установить их
расходимость.
b
b
dx
1
1
2
x dx lim
lim 1 1
1 x 2 blim
b b
b x
1
1
b
b
dx
dx
lim ln x 1 lim ln b ln 1
1 x blim
b
b
x
1
Интеграл расходится
0
0
cos x dx lim cos x dx lim sin x a lim sin a
a
a
0
a
a
Интеграл расходится,
так как такой предел не
существует
13
14.
1415.
Признак сравнения15
16.
Несобственный интеграл 2 родаПусть функция f(x) непрерывна на промежутке
и имеет бесконечный разрыв при x = b
[a; b )
b
lim f ( x )dx
Если существует конечный предел
0
a
то его называют несобственным интегралом второго рода и
обозначают:
b
b
f ( x )dx
f ( x )dx lim
a
0
a
В этом случае говорят, что несобственный интеграл сходится.
Если указанный предел не существует или он бесконечен, то
говорят, что несобственный интеграл расходится.
Аналогично, если функция терпит бесконечный разрыв в точке x = a,
то:
b
b
f ( x )dx
a
lim
0
f ( x )dx
a
16
17.
Если функция f(x) терпит разрыв во внутренней точке c отрезка[a; b] , то несобственный интеграл второго рода определяется
формулой:
b
c
b
a
a
c
f ( x )dx f ( x )dx f ( x )dx
В этом случае интеграл слева сходится лишь тогда, когда сходятся
оба интеграла справа.
В случае, когда f(x) > 0, и имеет
бесконечный разрыв в точке b, то
сходящийся несобственный интеграл 2
рода равен площади бесконечно
высокой криволинейной трапеции:
b
S f ( x )dx
a
y
0
a
x
b
17
18.
Пример.Вычислить несобственный интеграл или установить его
расходимость.
1
dx
1 x 2
0
1
dx
dx
2
2
lim
x
dx
lim
x
dx
1 x 2 0 x 2 0 1
0
0
0
1
1
1
1
1 1
1
1
lim
lim
lim
lim
0
0 x
0 x
1 0 1
1
1
2 lim 2
0
Интеграл расходится
18
19.
Несобственные интегралы от неограниченныхфункций. Примеры
Признак сравнения для
таких интегралов
19
20.
Несобственные интегралы от неограниченныхфункций. Признак сравнения
20
21.
Примеры.21


















 Математика
Математика








