Вычисление площадей и объемов. Лекция 5

1. Здравствуйте!

Лекция №5

2.

$ 17. Вычисление площадей и объемов
17.1. Площадь криволинейной трапеции
y
y = f (x)
x
a = x0
x1
x2
x3
b = xn
Рассмотрим фигуру, называемую криволинейной трапецией. Ее
границами являются: ось ОХ (внизу), прямые х=а (слева) и х=b
(справа) и кривая y f (x) (сверху) (см. рис.).

3.

Разобьем отрезок [a, b] на части a x0 x1 x2 ... xn 1 xn b и
пусть mi inf f ( x) и M i sup f ( x) . Составим величины
x [ xi , xi 1 ]
n 1
x [ xi , xi 1 ]
n 1
P* mi xi и P M i xi , в которых узнаем верхние и нижние
*
i 0
суммы
i 0
Дарбу.
Величины
I* lim P*
0
и
I * lim P*
0
называются
внутренней и внешней площадями криволинейной трапеции. Если
выполняется равенство I* I * P , то их общее значение и называется
площадью криволинейной трапеции.
Если функция f (x) интегрируема на отрезке [a, b] , то, вспоминая
теорию определенного интеграла, можно записать
b
P f ( x ) dx ,
a
что и определяет площадь криволинейной трапеции.

4.

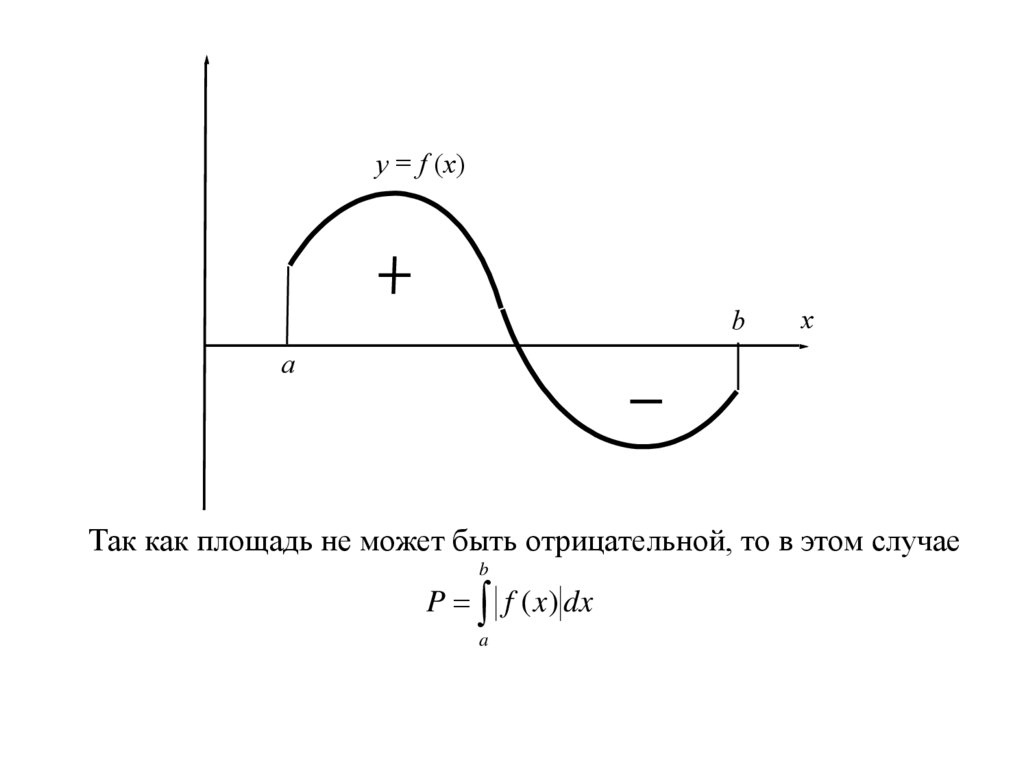
y = f (x)
b
x
a
Так как площадь не может быть отрицательной, то в этом случае
b
P f ( x) dx
a

5.

y
y = f1(x)
y = f2(x)
x
a
b
b
В этом случае очевидно, что P f1 ( x) f 2 ( x) dx
a

6.

y
y = f1(x)
y = f2(x)
x
a
b
b
Наконец, в этом случае P f1 ( x) f 2 ( x) dx .
a

7.

8.

17.2. Площадь криволинейного сектора
r = r ( )
O
Рассмотрим кривую r r ( ) , , заданную в полярных
координатах. Соединим концы кривой прямыми линиями с
полюсом системы координат. Получившаяся фигура называется
криволинейным сектором.

9.

Разобьем отрезок [ , ] на части 0 1 2 ... n 1 n и
пусть max i . Пусть далее ri inf r ( ) и Ri sup r ( ) .
[ i , i 1 ]
i
[ i , i 1 ]
1 n 1 2
1 n 1 2
*
Построим величины P* ri i и P Ri i , имеющие
2 i 0
2 i 0
смысл внутренней и внешней площадей криволинейного сектора.
Если lim P* lim P* P , то величина Р называется площадью
0
0
криволинейного сектора. Если функция r ( ) интегрируема на [ , ] ,
то
1 2
P r ( )d .
2
Пример. Вычислить площадь круга, полукруга, четверти круга.

10.

17.3. Объем тела вращения
y
y = f (x)
x
a
b
Представим себе, что имеется кривая y f (x) , заданная на отрезке
[a, b] . Пусть эта кривая вращается около оси ОХ. Получающееся
тело называется телом вращения

11.

Разобьем отрезок [a, b] на части a x0 x1 x2 ... xn 1 xn b и
определим mi inf f ( x) и M i sup f ( x) . На каждом отрезке
x [ xi , xi 1 ]
x [ xi , xi 1 ]
построим цилиндр с радиусом основания mi и высотой xi . Все эти
цилиндры будут вписаны в наше тело вращения и их общий объем
n 1
будет равен V* mi2 xi .
i 0
Далее, на каждом отрезке построим цилиндр с радиусом
основания M i и высотой xi . Все эти цилиндры будут описаны
около нашего тело вращения и их общий объем будет равен
n 1
V M i2 xi .
*
i 0
Если lim V* lim V * V , то величина V называется объемом тела
0
0
вращения. Если функция f (x) интегрируема на [a, b] , то очевидно,
что
b
V f 2 ( x) dx
a

12.

Пример. Объём шара
y
y=
2
R-x
2
x
-R
R
Очевидно, что шар получается вращением полуокружности около
оси ОХ. Поэтому объем шара
3 R
x
V R 2 x 2 dx R 2 x
R
3
R
R
R
R
3
R
4
R 2 2 R 2 R 3 .
3 3

13.

$.18. Несобственные интегралы первого рода
Пусть
1. функция f (x) определена на отрезке [a, ) ;
A
2. A a существует
f ( x)dx .
a
Произведем
теперь
предельный
переход
A .
Тогда
A
lim
A
f ( x)dx
называется несобственным интегралом первого рода
a
и обозначается символом f ( x ) dx :
lim
A
A
a
a
a
f ( x)dx = f ( x)dx .
Если этот предел существует и конечен, то говорят, что
несобственный интеграл сходится (или: существует). Если этот
предел равен бесконечности или вообще не существует, то говорят,
что несобственный интеграл расходится (или: не существует).

14.

Совершенно
аналогично
определяются
несобственные интегралы первого рода:
a
f ( x)dx
f ( x)dx
и
a
lim
B
lim
B
f ( x)dx ,
B
a
A
f ( x)dx lim f ( x)dx (а любое).
B
A
a
следующие

15.

Простейшие свойства несобственных интегралов первого
рода
1. Если сходится f ( x ) dx , то b a сходится и
a
Наоборот, если
f ( x)dx .
b
b
f ( x)dx сходится и существует f ( x)dx , то сходится
b
a
и f ( x ) dx . При этом верно соотношение
a
b
a
a
b
A
b
A
a
a
b
f ( x)dx f ( x)dx f ( x)dx .
Доказательство. Пусть A b a . Тогда имеем
f ( x)dx f ( x)dx f ( x)dx .
Сделаем предельный переход А :
lim
A
A
b
a
a
A
f ( x)dx f ( x)dx lim f ( x)dx .
A
b

16.

Так как предел слева существует, то существует и предел справа и
f ( x)dx сходится и соотношение принимает вид
b
b
a
a
b
f ( x)dx f ( x)dx f ( x)dx .
Подумайте сами, что надо изменить в предыдущей фразе, чтобы
доказать обратное утверждение.

17.

2. Если
f ( x)dx сходится, то
a
lim
A
Доказательство.
Согласно предыдущему пункту
f ( x)dx 0
A
A
a
a
A
A
A
a
a
f ( x)dx f ( x)dx f ( x)dx
Отсюда
f ( x)dx f ( x)dx f ( x)dx .
Делая предельный переход А , получаем
lim
A
A
a
A
f ( x)dx f ( x)dx lim f ( x)dx
A
a
a
f ( x)dx f ( x)dx 0.
a

18.

3. Если сходятся
a
a
f ( x)dx и g ( x)dx , то сходится также и
( f ( x) g ( x))dx и верно соотношение
a
a
a
a
( f ( x) g ( x))dx = f ( x)dx ± g ( x)dx .
Доказательство. Имеем
A
A
A
a
a
a
( f ( x) g ( x))dx f ( x)dx g ( x)dx .
Делая предельный переход А , получаем
A
( f ( x) g ( x))dx lim ( f ( x) g ( x))dx
A
a
A
lim
A
a
A
a
a
a
f ( x)dx lim g ( x)dx f ( x)dx g ( x)dx.
a
A

19.

4. Если сходятся
a
a
f ( x)dx и с константа, то сходится и cf ( x)dx и
верна формула
a
a
cf ( x)dx c f ( x)dx .
Доказательство. Имеем
A
A
a
a
cf ( x)dx c f ( x)dx .
Делая предельный переход А , получаем
cf ( x)dx
a
A
lim cf ( x)dx c lim
A
a
A
A
f ( x)dx c f ( x)dx
a
a
.