Определённый интеграл. Площадь плоской фигуры

1.

2.

8. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
8.1 Определения и свойства
8.2. Вычисление определённого
интеграла
8.3. Приложения определённого
интеграла

3.

8. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
8.3. Приложения определённого интеграла
8.3.1 Площадь плоской фигуры
8.3.2 Объём тела вращения
8.3.3 Длина дуги плоской кривой

4.

8.3.1 ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ
Вспомним геометрический смысл определённого интеграла:
Определённый интеграл от неотрицательной функции численно равен
площади криволинейной трапеции.
b
Sкр тр f ( x)dx
a
a
y
0
y f ( x)
b
x

5.

8.3.1 ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ
Криволинейная трапеция – частный случай плоской фигуры.
Плоские фигуры могут быть расположены по-разному.

6.

8.3.1 ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ
1
Пусть даны две функции 0 g(x) f(x)
непрерывные на отрезке
a; b .
y
y f ( x)
S
0
a
y g ( x)
b
x
b
b
a
a
S f ( x)dx g ( x)dx
b
S f ( x) g ( x) dx
a
Площадь плоской фигуры,
ориентированной по оси Оу.
Замечание
Формула справедлива, если g(x) f(x)
и хотя бы одна из функций или её часть 0 при
x a; b .

7.

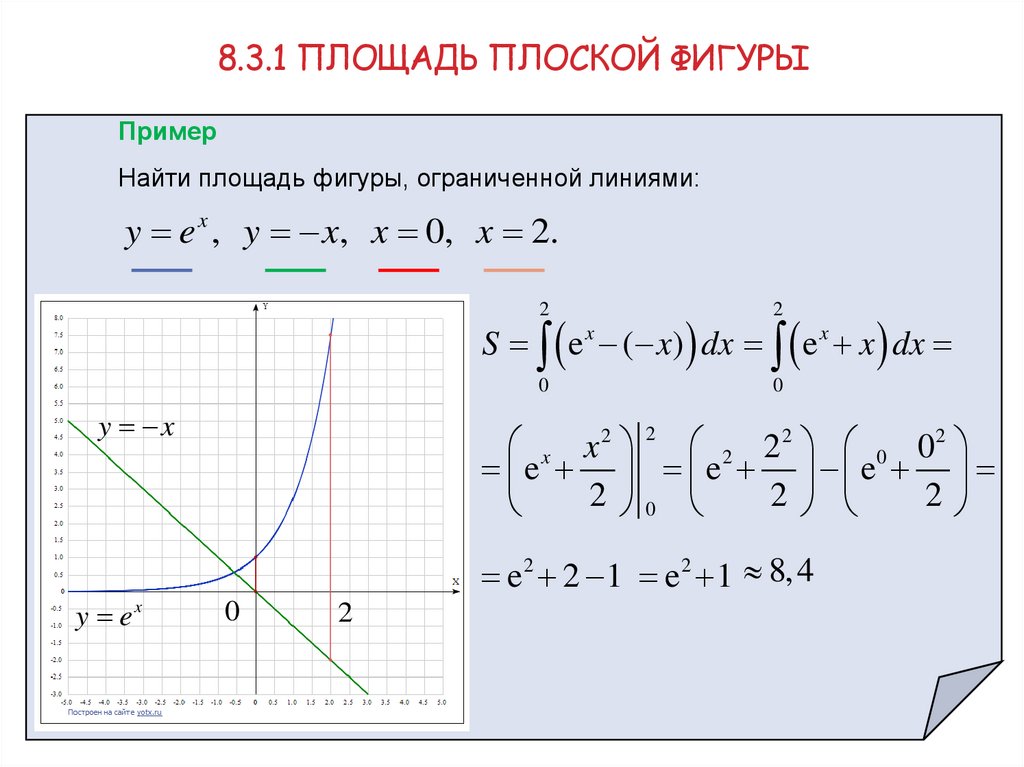
8.3.1 ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ
Пример
Найти площадь фигуры, ограниченной линиями:
y e x , y x, x 0, x 2.
2
2
0
0
S e x ( x) dx e x x dx
y x
x x 2 2 2 22 0 02
e e e
2 0
2
2
e 2 2 1 e 2 1 8, 4
y ex
0
2

8.

8.3.1 ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ
2
Пусть даны две функции 0 (y) (y)
непрерывные на отрезке
y
x ( y)
c; d .
x ( y)
d
d
d
c
c
S ( y )dy ( y )dy
S
c
d
0
x
S ( y ) ( y ) dy
c
Площадь плоской фигуры,
ориентированной по оси Оx.
Замечание
Формула справедлива, если (y) (y)
и хотя бы одна из функций или её часть 0 при
y c; d .
Замечание (для пунктов 1 и 2)
Если задана сложная фигура, то её нужно разбить на более простые
прямыми, параллельными оси Ox или оси Oy.

9.

8.3.1 ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ
Пример
Найти площадь фигуры, ограниченной линиями:
y
x y 2 , x , y 0, y 2.
2
y x , y 2 x, y 2.
y
y 2 x x
2
2
y
2
2 y
S y ( ) dy y dy
2
2
0
0
2
y x
x y
2
0
2
y 3 y 2 2 23 2 2
3 4
3 2 2 0
8
11
2
1 3 3,7
3
3
3

10.

8.3.2 ОБЪЁМ ТЕЛА ВРАЩЕНИЯ
Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная
линиями: y=f(x), y=0, x=a, x=b.
Функция y=f(x) – непрерывна и неотрицательна на отрезке a; b .
y
0 a
y f (x)
b
x

11.

8.3.2 ОБЪЁМ ТЕЛА ВРАЩЕНИЯ
1) Разобьём отрезок
a; b на n частичных отрезков.
2) В каждом частичном отрезке выберем произвольную точку ci .
f ci , i 1,2,..., n.
4) Длина каждого частичного отрезка xi xi xi 1.
3) Вычислим значение функции в ней
f (ci )
x0
x1 x2 x3
c1 c2
c3
xi 1
xi
ci
xn 1 xn
cn

12.

8.3.2 ОБЪЁМ ТЕЛА ВРАЩЕНИЯ
5) Разобьём тело вращения плоскостями, перпендикулярными оси Ох и
проходящими через точки xi на слои.
6) Ограничим слои цилиндрами с высотой xi и радиусом
7) Объём каждого цилиндра
f (ci ).
Vi Sосн H f 2 (ci ) xi .

13.

9.3.2 ОБЪЁМ ТЕЛА ВРАЩЕНИЯ
8) Объём тела вращения приближённо равен сумме объёмов полученных
цилиндров:
n
n
i 1
i 1
Vт вр Vi f 2 (ci ) xi .
Чем меньше длины частичных отрезков, тем точнее приближение.

14.

8.3.2 ОБЪЁМ ТЕЛА ВРАЩЕНИЯ
9) Перейдём к пределу при
n
n (d 0)
b
b
a
a
2
2
f
(
x
)
dx
f
Vт вр lim f (ci ) xi
( x)dx
2
d 0
i 1
Замечание
Пусть вокруг оси Оy вращается криволинейная трапеция, ограниченная
линиями: x= (y), x=0, y=c, y=d.
Функция x= (y) – непрерывна и неотрицательна на отрезке c; d .
y
d
x ( y)
Тогда
d
Vт вр 2 ( y )dy
c
c
0
x

15.

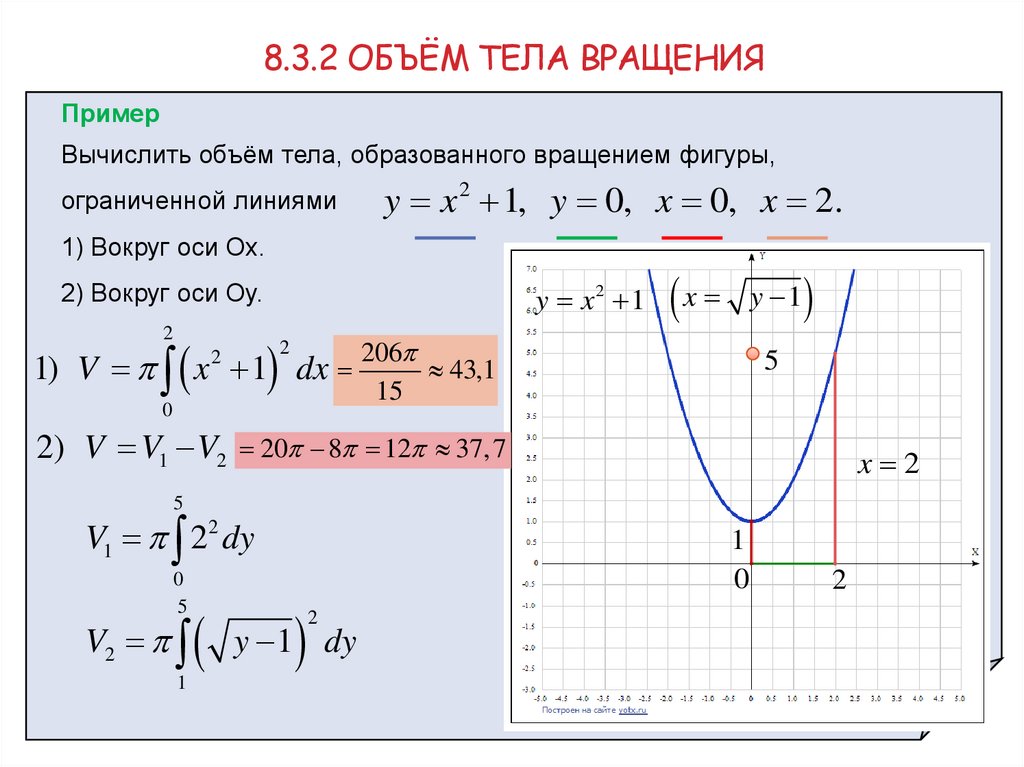
8.3.2 ОБЪЁМ ТЕЛА ВРАЩЕНИЯ
Пример
Вычислить объём тела, образованного вращением фигуры,
ограниченной линиями
y x 2 1, y 0, x 0, x 2.
1) Вокруг оси Ox.
2) Вокруг оси Oy.
2
y x2 1
1) V x 1 dx
2
2
0
x y 1
206
43,1
15
5
2) V V1 V2 20 8 12 37,7
x 2
5
V1 22 dy
0
5
V2
1
1
0
y 1 dy
2
2

16.

8.3.3 ДЛИНА ДУГИ ПЛОСКОЙ КРИВОЙ
Пусть функция y = f(x) определена и непрерывна на отрезке
a; b .
Требуется найти длину линии (дуги) AB.
1) Разобьём весь отрезок на n частичных отрезков
2) В каждом частичном отрезке выберем произвольную точку ci .
3) Длина каждого частичного отрезка
xi xi xi 1.
Сделаем дополнительные построения
y
A
x0
x1
x2 x3
a c1 c2
c3
B
xi
xi 1
0
ci
xn 1
cn b
y f ( x)
xn
x

17.

8.3.3 ДЛИНА ДУГИ ПЛОСКОЙ КРИВОЙ
Li
M i 1
4)
yi
5) Длина гипотенузы: Li M i 1M i
Li
xi
По теореме Лагранжа: если
У нас:
yi f xi f xi 1
Mi
xi yi
2
2
c a; b ,то f b f a f c b a .
ci xi 1; xi , тогда f xi f xi 1 f ci xi xi 1 .
yi f ci xi
Получаем:
Li
xi f ci xi
2
2
1 f ci
2
xi 1 f ci xi
2
2

18.

8.3.3 ДЛИНА ДУГИ ПЛОСКОЙ КРИВОЙ
6) Длина дуги AB приближённо равна длине ломаной линии Ln :
n
n
i 1
i 1
AB Ln Li 1 f ci xi .
2
Чем меньше длины частичных отрезков, тем точнее приближение.
7) Перейдём к пределу при
n (d 0)
b
AB lim 1 f ci xi 1 f x dx
n
d 0
2
i 1
2
a
b
Длина дуги плоской кривой
l 1 f x dx
2
a
Замечание
Если функция задана как x= (y)
и она непрерывна при
y c; d , то
d
l 1 y dy
c
2

19.

8.3.3 ДЛИНА ДУГИ ПЛОСКОЙ КРИВОЙ
Замечание
x x t
Пусть функция задана параметрически:
y y t
Пусть x a, x b x a; b .
Тогда
x x t
1 y x dx
dx xt dt
b
l
2
a
2
yt
1 xt dt
xt
Длина дуги плоской кривой
для функции,
заданной параметрически
xt yt
2
xt
2
2
t ;
tв
tн
yt
y x
xt
xt dt
xt yt dt
2
2
l
xt yt dt
2
2

20.

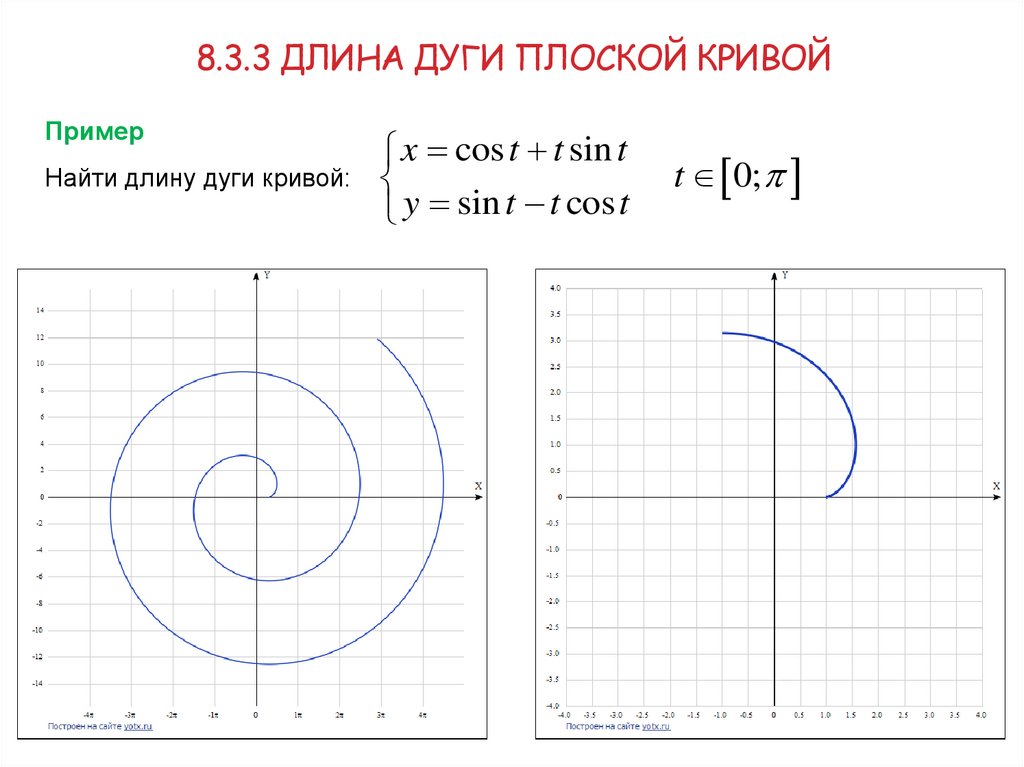
8.3.3 ДЛИНА ДУГИ ПЛОСКОЙ КРИВОЙ
Пример
Найти длину дуги кривой:
x cos t t sin t
y sin t t cos t
t 0;

21.

8.3.3 ДЛИНА ДУГИ ПЛОСКОЙ КРИВОЙ
Пример
x cos t t sin t
y sin t t cos t
Найти длину дуги кривой:
l
t 0;
xt yt dt
2
2
xt cos t t sin t sin t sin t t cos t t cos t
yt sin t t cos t cos t cos t t sin t t sin t
l
0
0
0
t cos t t sin t dt t 2 cos2 t sin 2 t dt tdt
2
2
2
2
t2
4,93
0
2
2
2 0

22.

8.3 ПРИЛОЖЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
Профессионально-ориентированная задача
Описание ситуации
Господин А. приобрёл под застройку участок земли сложной формы на берегу
моря. По документам площадь участка равна 1,6 гектара.
Три стороны участка расположены на суше и являются сторонами квадрата.
Четвёртая сторона проходит по береговой линии, напоминающей параболу,
выступает в море и симметрична. Ширина участка 120 м, бóльшая длина
равна 140 м, меньшая – 120 м (см. рисунок).

23.

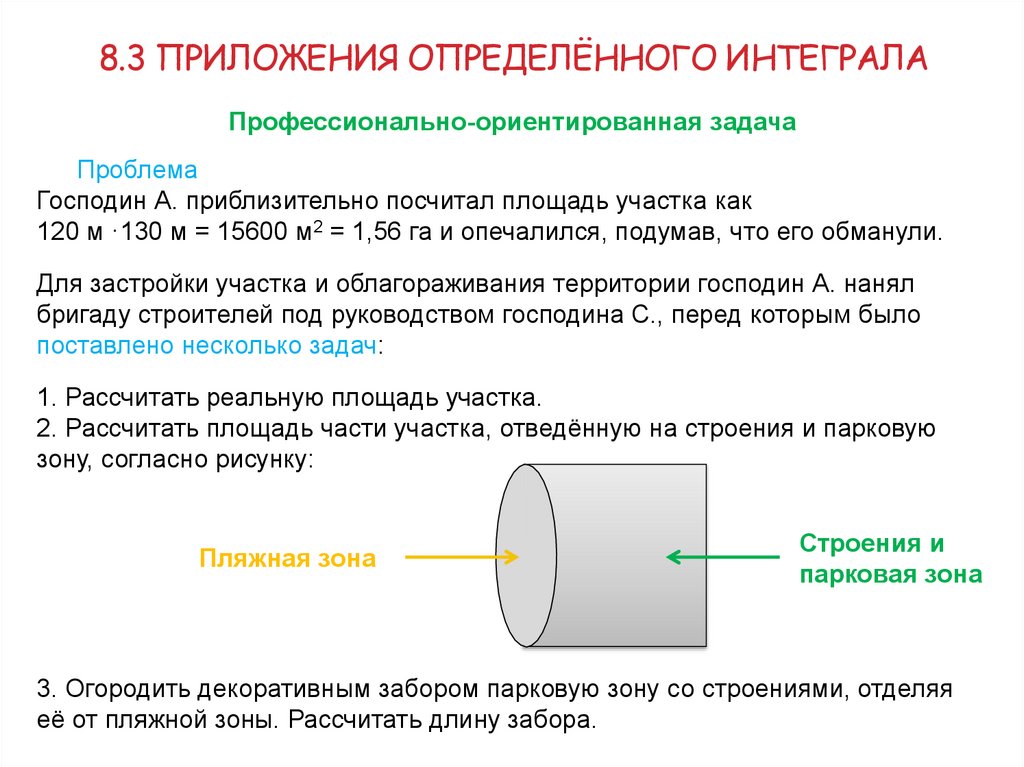
8.3 ПРИЛОЖЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
Профессионально-ориентированная задача
Проблема
Господин А. приблизительно посчитал площадь участка как
120 м ·130 м = 15600 м2 = 1,56 га и опечалился, подумав, что его обманули.
Для застройки участка и облагораживания территории господин А. нанял
бригаду строителей под руководством господина С., перед которым было
поставлено несколько задач:
1. Рассчитать реальную площадь участка.
2. Рассчитать площадь части участка, отведённую на строения и парковую
зону, согласно рисунку:
Пляжная зона
Строения и
парковая зона
3. Огородить декоративным забором парковую зону со строениями, отделяя
её от пляжной зоны. Рассчитать длину забора.

24.

8.3 ПРИЛОЖЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
Профессионально-ориентированная задача
Задача решена на лекции очно.

25.

ПРОДОЛЖЕНИЕ СЛЕДУЕТ...