Теорема о площади треугольников

1.

2.

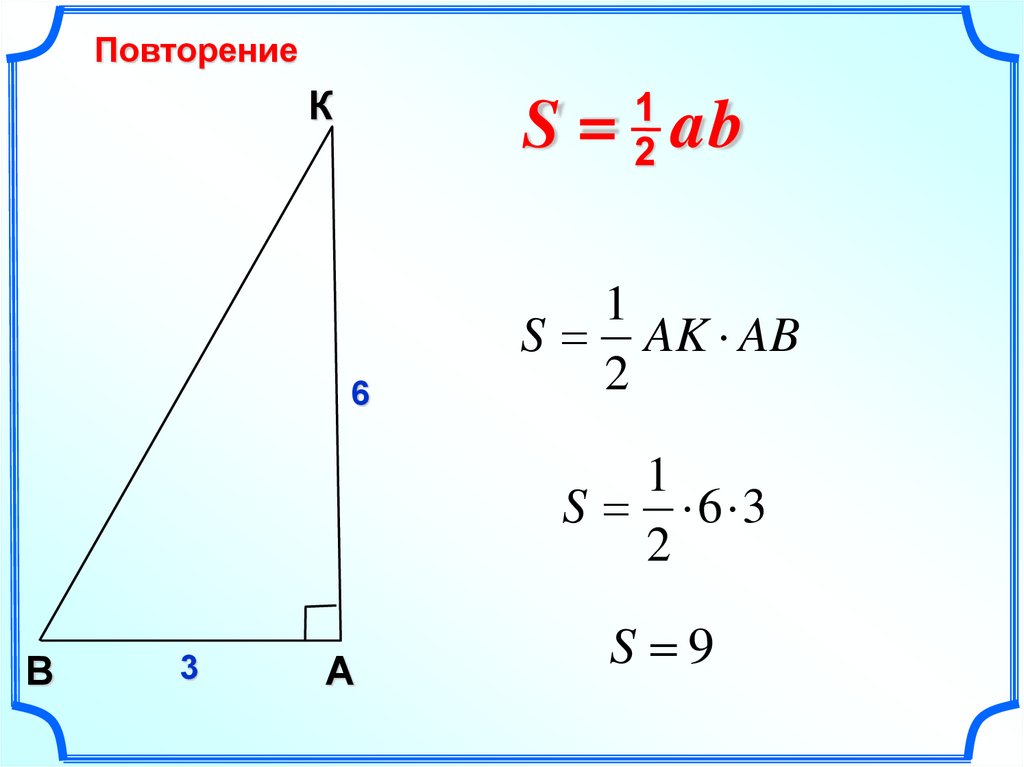
Повторение
К
1
2
S = ab
6
1
S AK AB
2
1
S 6 3
2
В
3
A
S 9

3.

Повторение
1
2
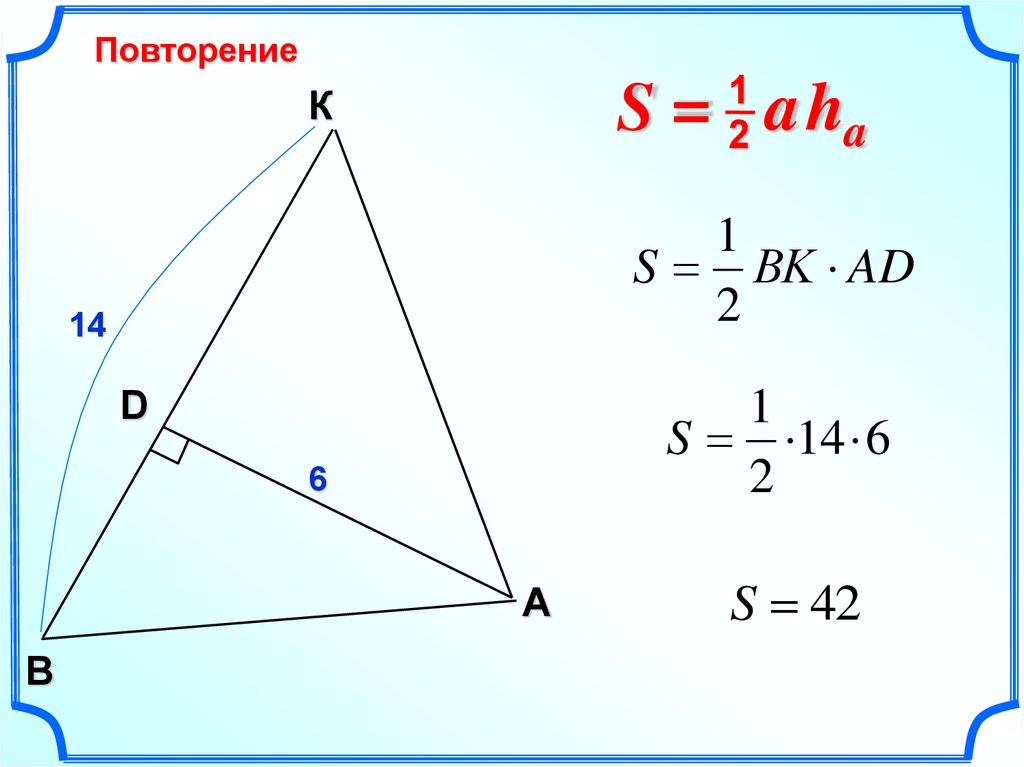
S = aha
К
1
S ВK AD
2
14
1
S 14 6
2
D
6
A
В
S 42

4.

Повторение
1
2
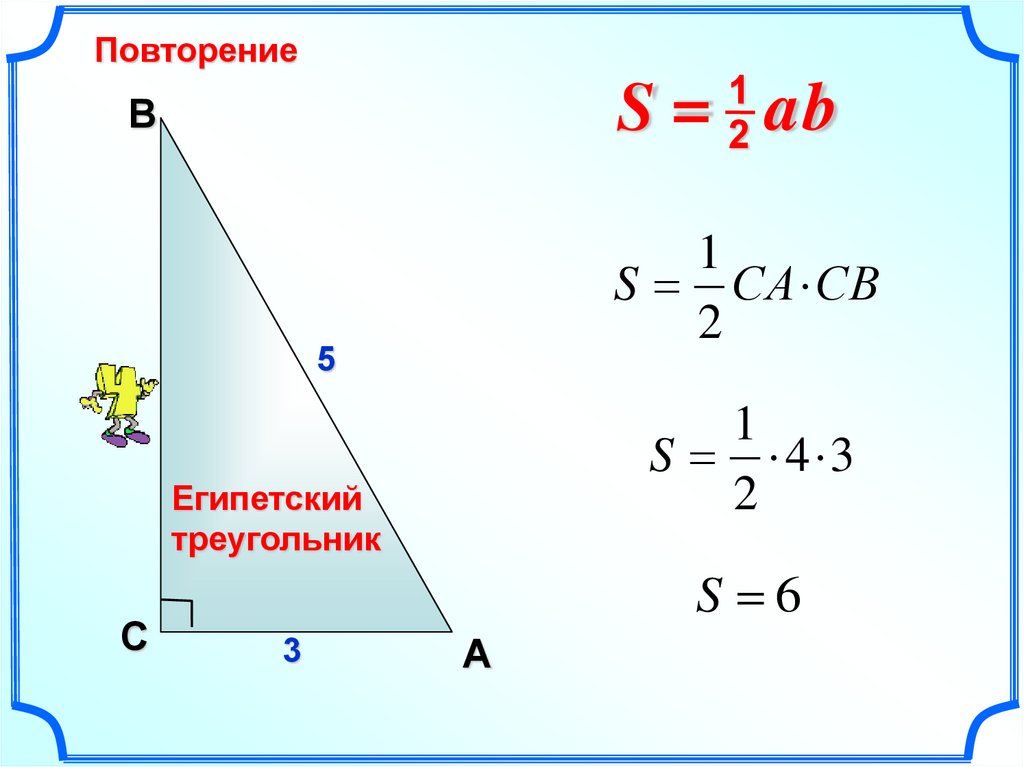
S = ab
В
1
S СА СB
2
5
1
S 4 3
2
Египетский
треугольник
С
S 6
3
A

5.

Формула
Герона
S = p(p – a)(p – b)(p – c)
р - полупериметр
Повторение
В
5
6 6
6
A
7
С
S 9(9 5)(9 6)(9 7) 9 4 3 2 3 2 6

6.

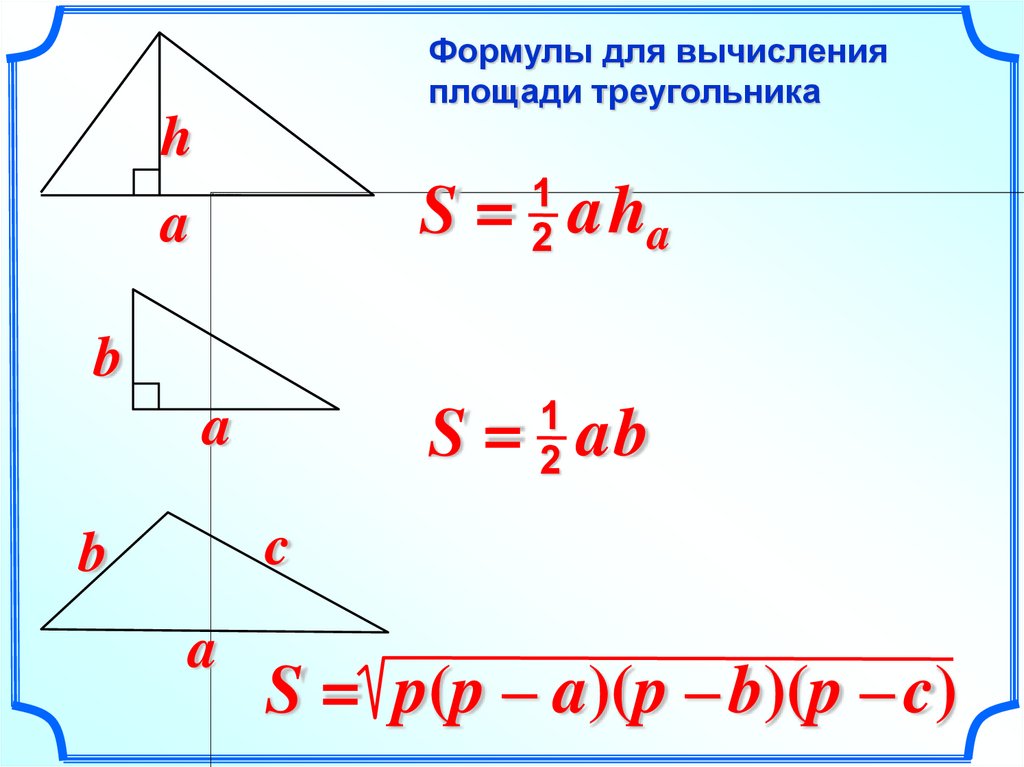
Формулы для вычисления
площади треугольника
h
1
2
S = aha
a
b
1
2
a
S = ab
c
b
a
S = p(p – a)(p – b)(p – c)

7.

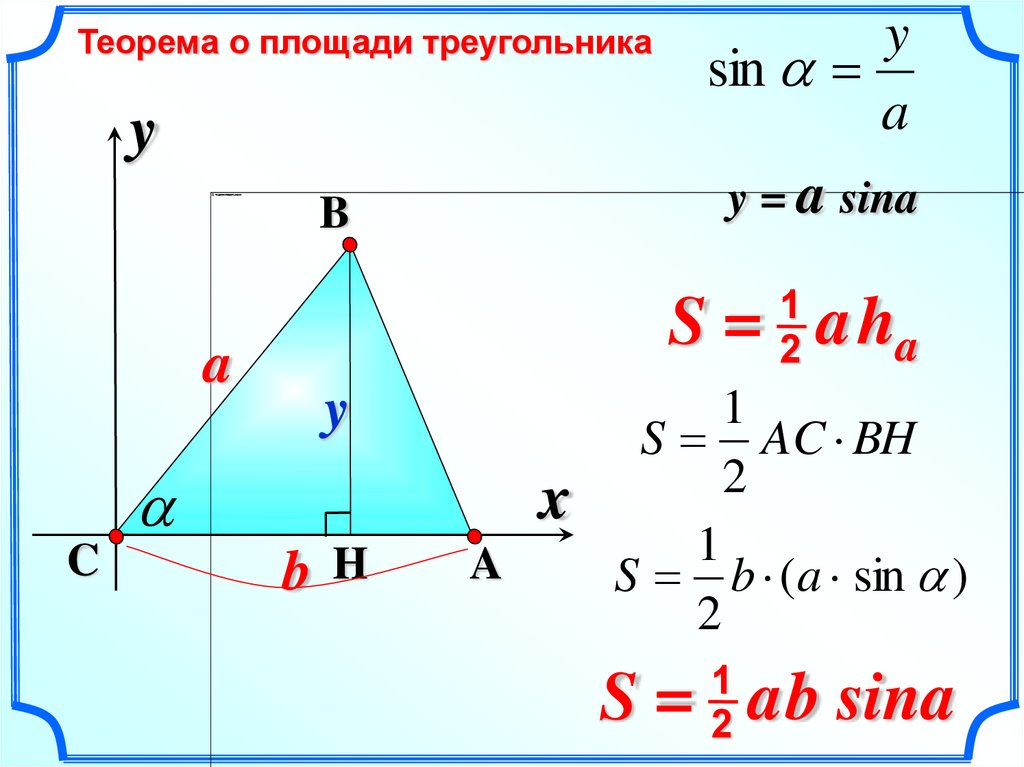
Теорема о площади треугольника
y
y = a sina
B
a
1
2
S = aha
y
C
y
sin
a
x
bH
A
1
S AC BH
2
1
S b (a sin )
2
1
2
S = ab sina

8.

B
1
S AB BC sin B
2
1
S AС BА sin А
2
1
S AС BС sin С
2
C
A

9.

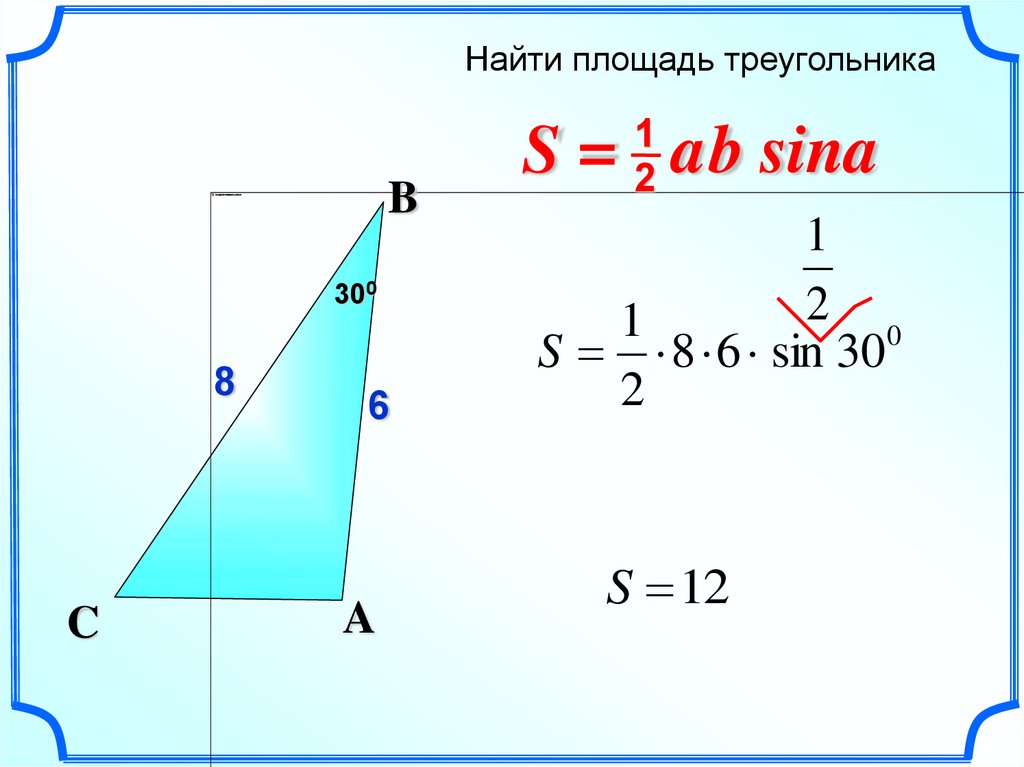
Найти площадь треугольника
B
300
8
C
6
A
1
2
S = ab sina
1
2
1
0
S 8 6 sin 30
2
S 12

10.

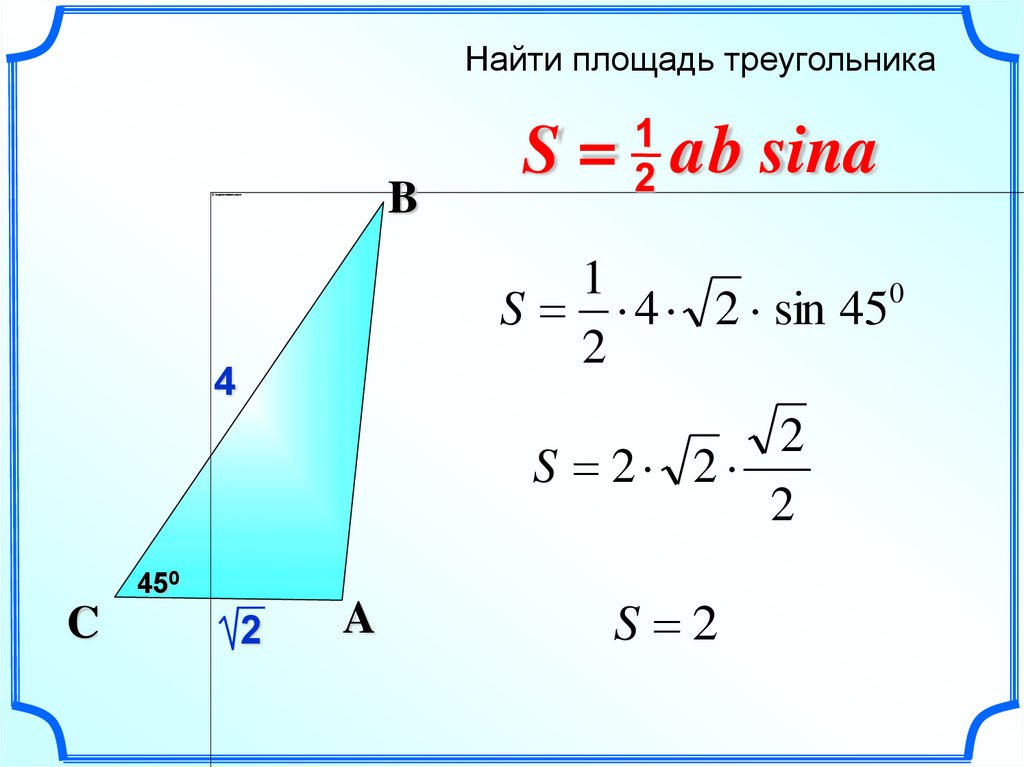
Найти площадь треугольника
B
1
2
S = ab sina
1
0
S 4 2 sin 45
2
4
2
S 2 2
2
450
C
2
A
S 2

11.

Найти BC
1
2
S = ab sina
S = 3 см2
B
300
2
6
?
A
C
1
0
3 2 b sin 30
2
1
3 b
2
2
b 6

12.

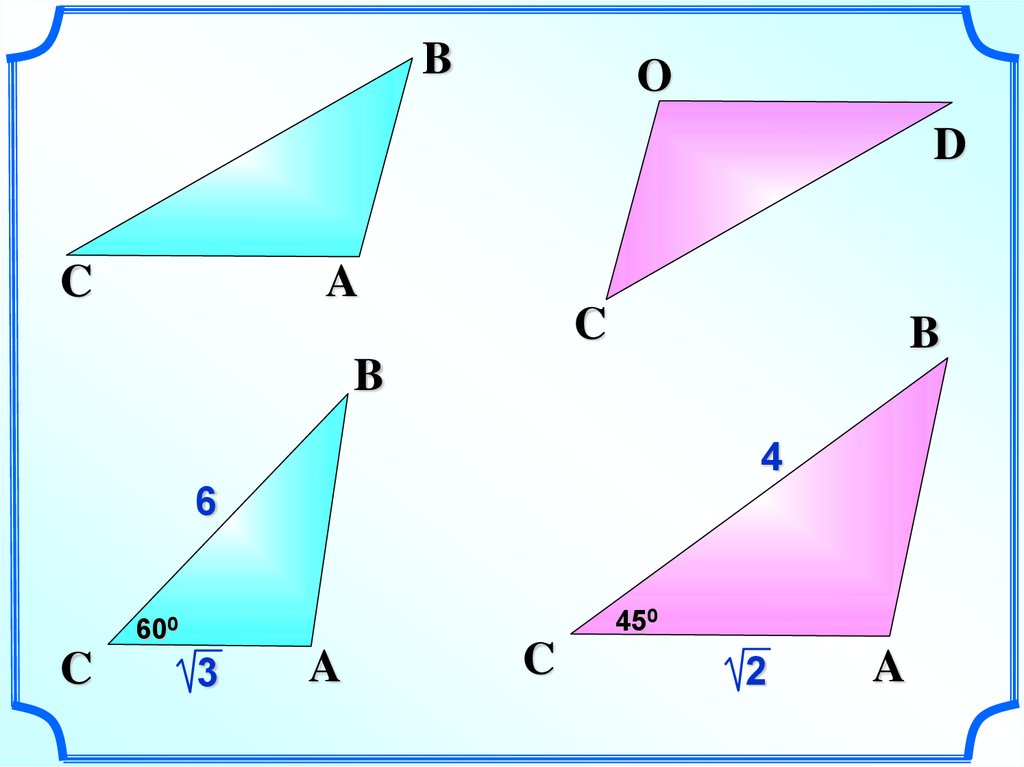
B
O
D
C
A
C
B
B
4
6
450
600
C
3
A
C
2
A

13.

Найти B
S = 2 3 см2
1
2
S = ab sina
B
1
2 3 2 4 sin
2
600
4
2
2 3 4 sin :4
A
C
3
sin
2
B
4
C
1200
2
A
1 60
0
2 120
0

14.

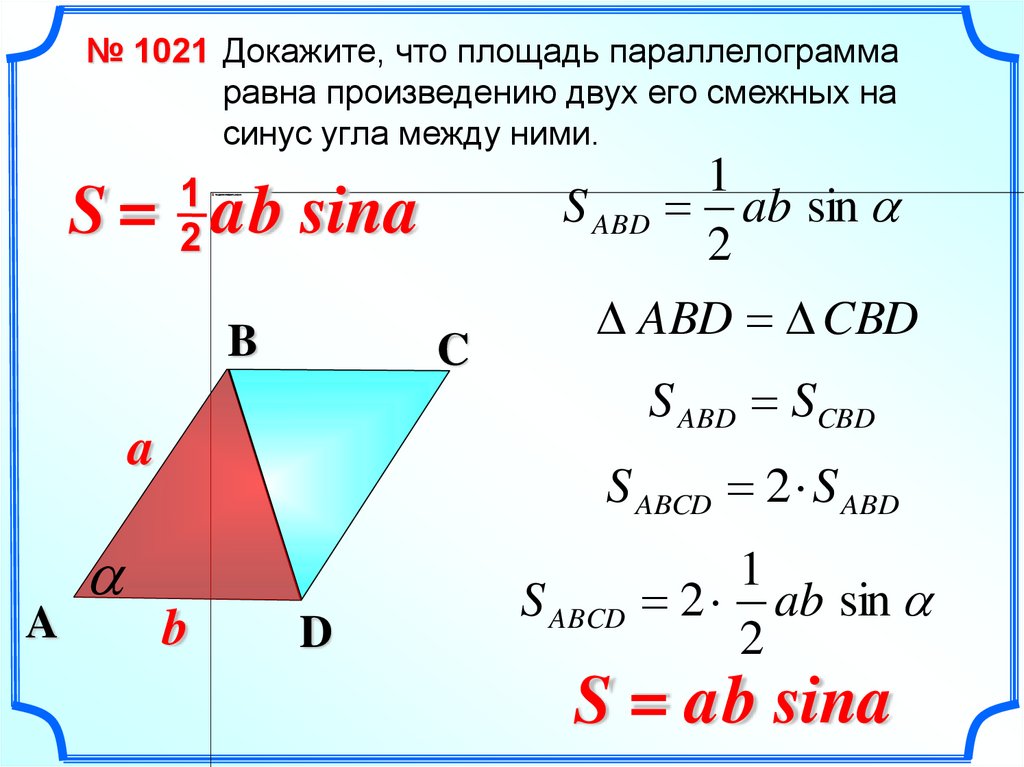
№ 1021 Докажите, что площадь параллелограмма
равна произведению двух его смежных на
синус угла между ними.
1
2
S = ab sina
B
C
a
A
S ABD
1
ab sin
2
ABD CBD
S ABD SCBD
S ABCD 2 S ABD
b
D
S ABCD
1
2 ab sin
2
S = ab sina

15.

B
C
d1
2
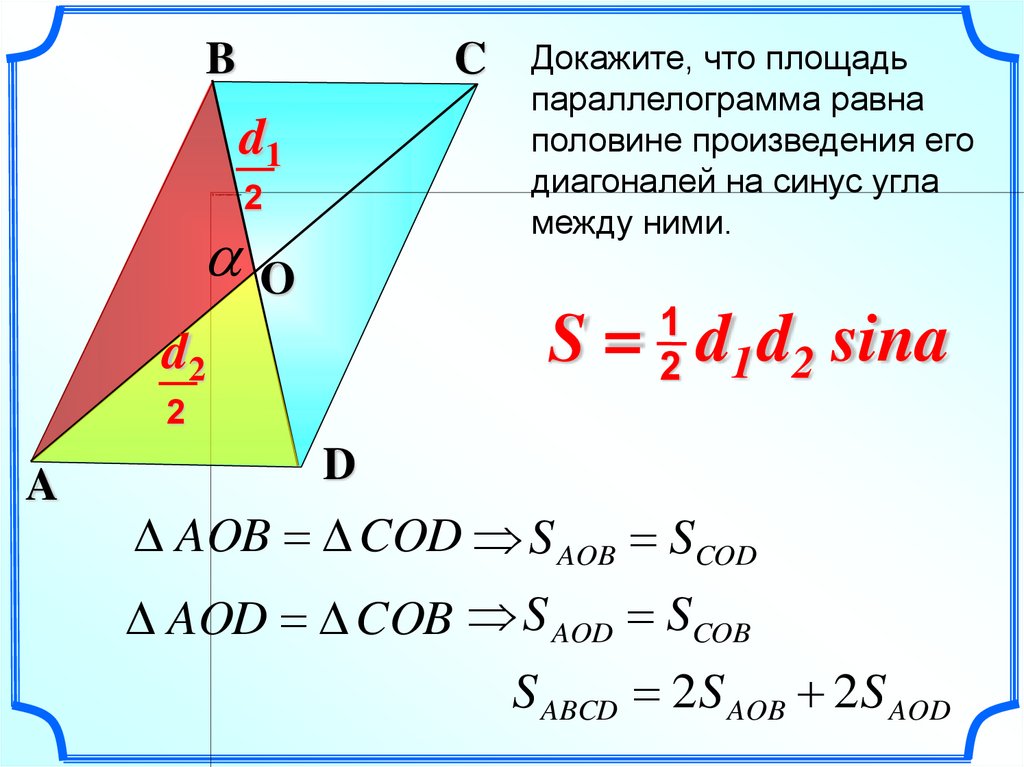
Докажите, что площадь
параллелограмма равна
половине произведения его
диагоналей на синус угла
между ними.
O
1
2
S = d1 d2 sina
d2
2
A
D
AOB COD S AOB SCOD
AOD COB S AOD SCOB
S ABCD 2S AOB 2S AOD

16.

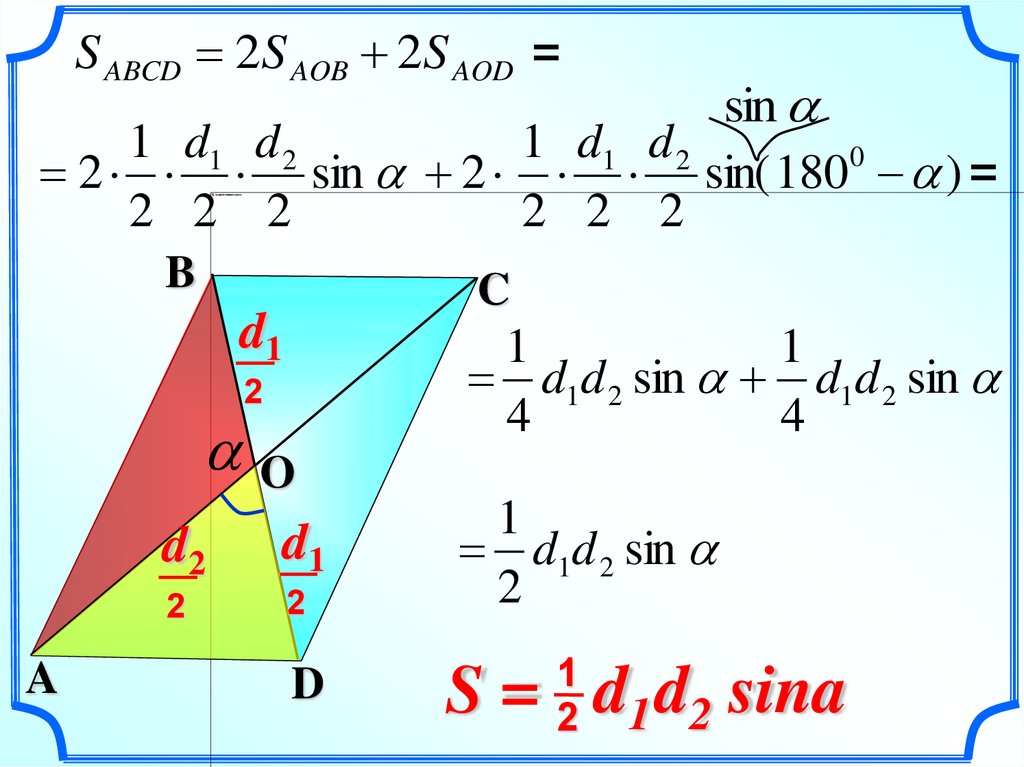
S ABCD 2S AOB 2S AOD =
sin
1 d1 d 2
1 d1 d 2
0
2 sin 2 sin( 180 ) =
2 2 2
2 2 2
B
C
d1
A
1
1
d1d 2 sin d1d 2 sin
4
4
2
O
d2
d1
2
2
D
1
d1d 2 sin
2
1
2
S = d1 d2 sina

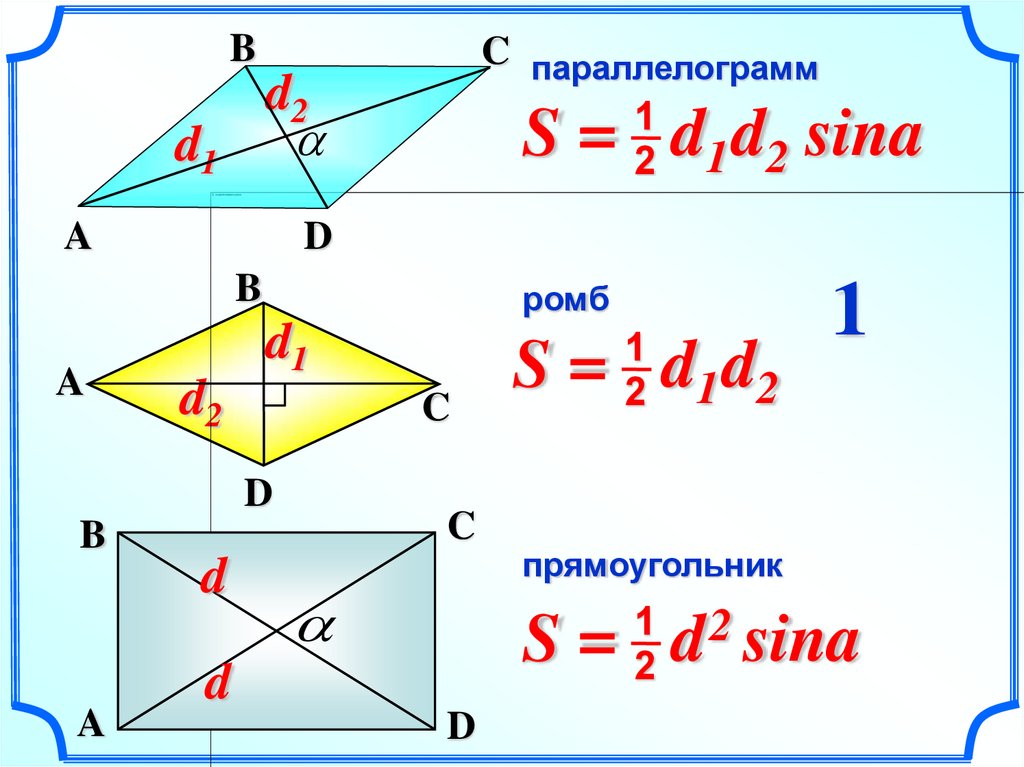
17.

B
a
1
2
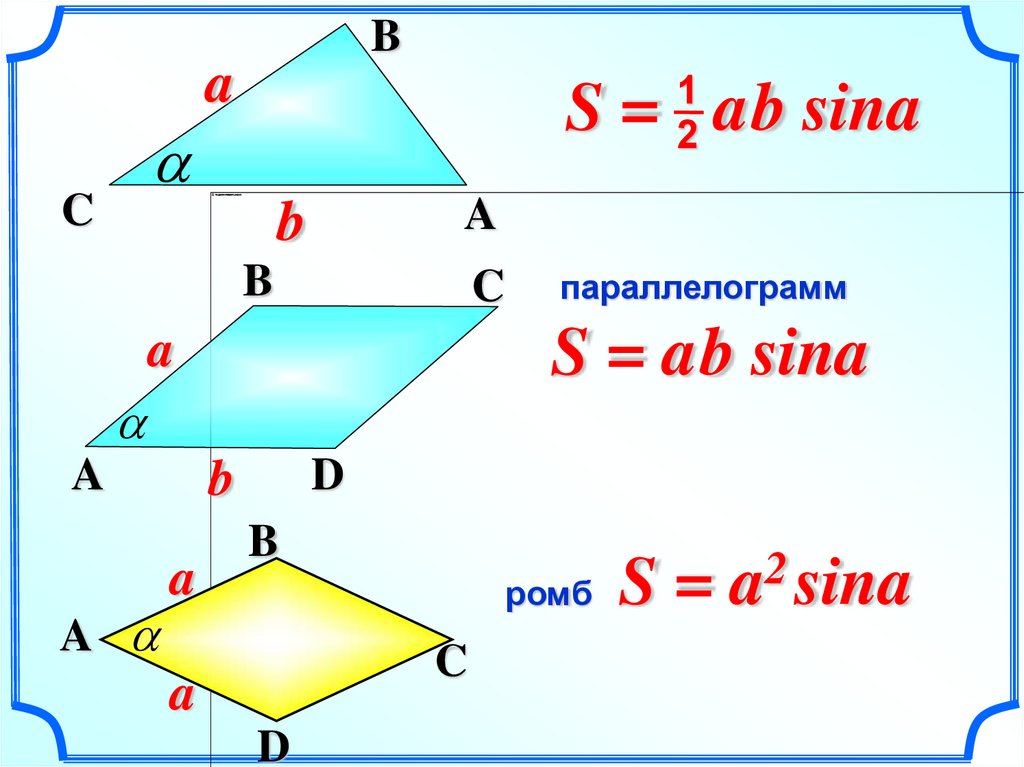
S = ab sina
C
A
b
B
C
S = ab sina
a
A
A
D
b
a
параллелограмм
B
ромб
C
a
D
S=
2
a sina

18.

B
C параллелограмм
1
2 1 2
d2
d1
A
S = d d sina
D
B
A
ромб
d1
d2
C
D
C
B
d
A
1
2
S = d1 d2 sin900
прямоугольник
S=
d
D
1
1
2
2
d sina

19.

B
C
АВСD – параллелограмм,
АВ = 6, AD = 4.
Найти SABCD
6
S = ab sina
600
A
4
S ABCD
D
3
4 6 sin 60 4 6
12 3
2
0

20.

Найти SABCD
B
450
4
4
A
2
a sina
S=
C
S 4 sin 45
2
2
S 16
2
D
S 8 2
0

21.

B
C
Найти SABCD
1350
1
2
12
A
S = d1 d2 sina
D
0
S ABCD
АВСD – прямоугольник,
АС = 12.
sin
45
1
2
0 1
12 12 sin 135 12 12
36 2
2
2
2

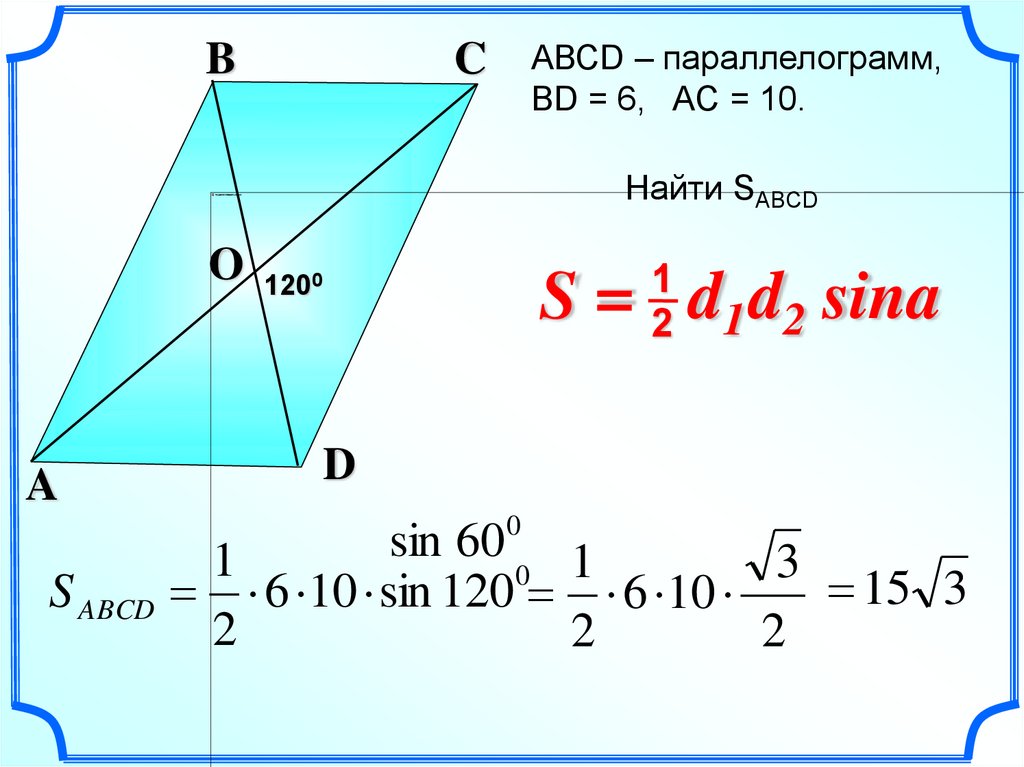
22.

B
АВСD – параллелограмм,
ВD = 6, AC = 10.
C
Найти SABCD
O
A
1
2
S = d1 d2 sina
1200
D
0
S ABCD
sin
60
1
3
0 1
15 3
6 10 sin 120 6 10
2
2
2

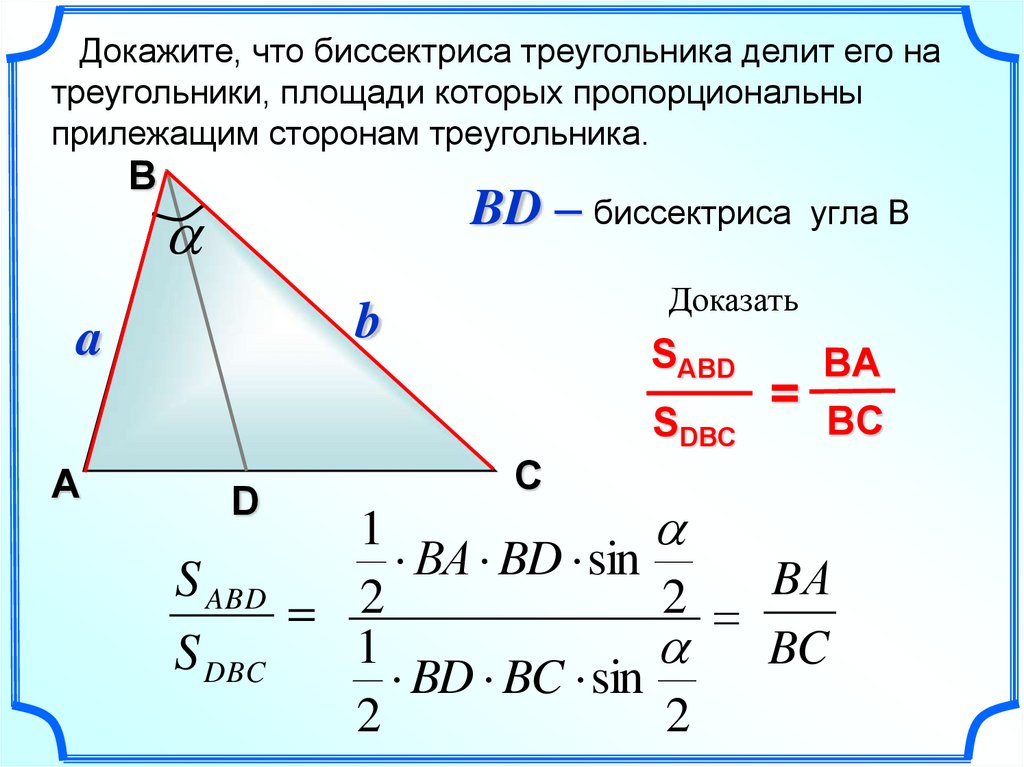
23.

Докажите, что биссектриса треугольника делит его на
треугольники, площади которых пропорциональны
прилежащим сторонам треугольника.
В
BD – биссектриса
Доказать
b
a
SАBD
SDВС
A
D
S ABD
S DBC
угла В
С
=
BA
ВC
1
ВA BD sin
BА
2
2
1
BC
BD BC sin
2
2

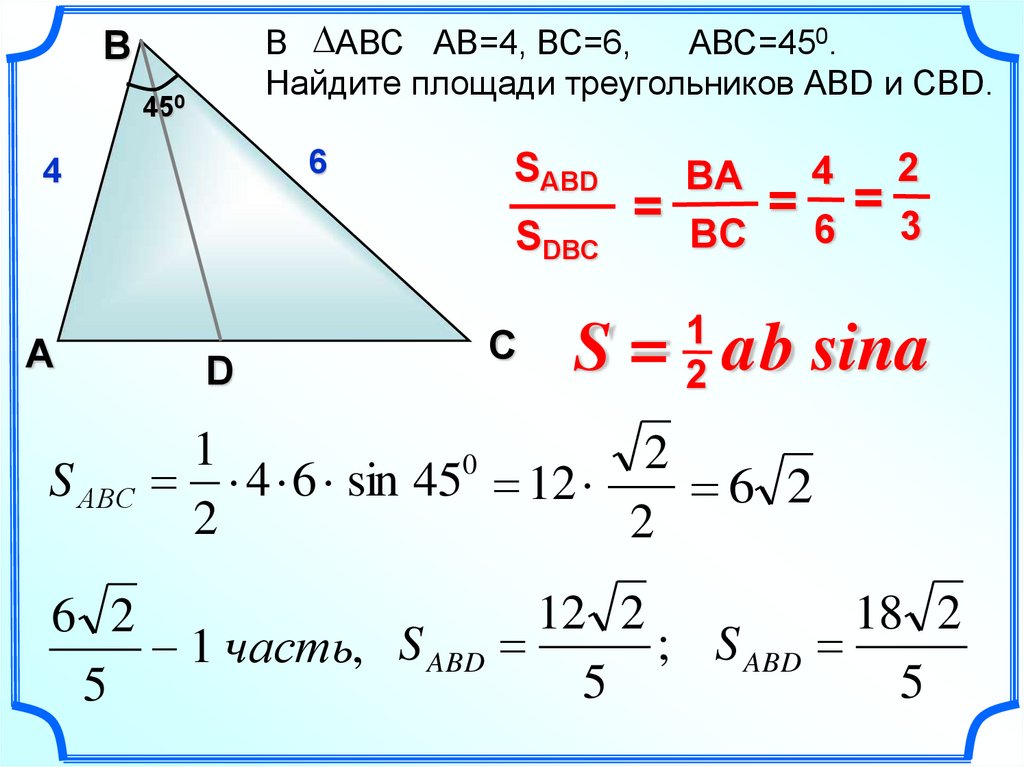
24.

В АВС АВ=4, ВС=6,
АВС=450.
Найдите площади треугольников АВD и СВD.
В
450
6
4
SАВD
SDВС
A
S АВС
D
С
=
BА
ВC
=
4
6
=
2
3
1
2
S = ab sina
1
2
0
4 6 sin 45 12
6 2
2
2
12 2
18 2
6 2
; S ABD
1 часть, S ABD
5
5
5

25.

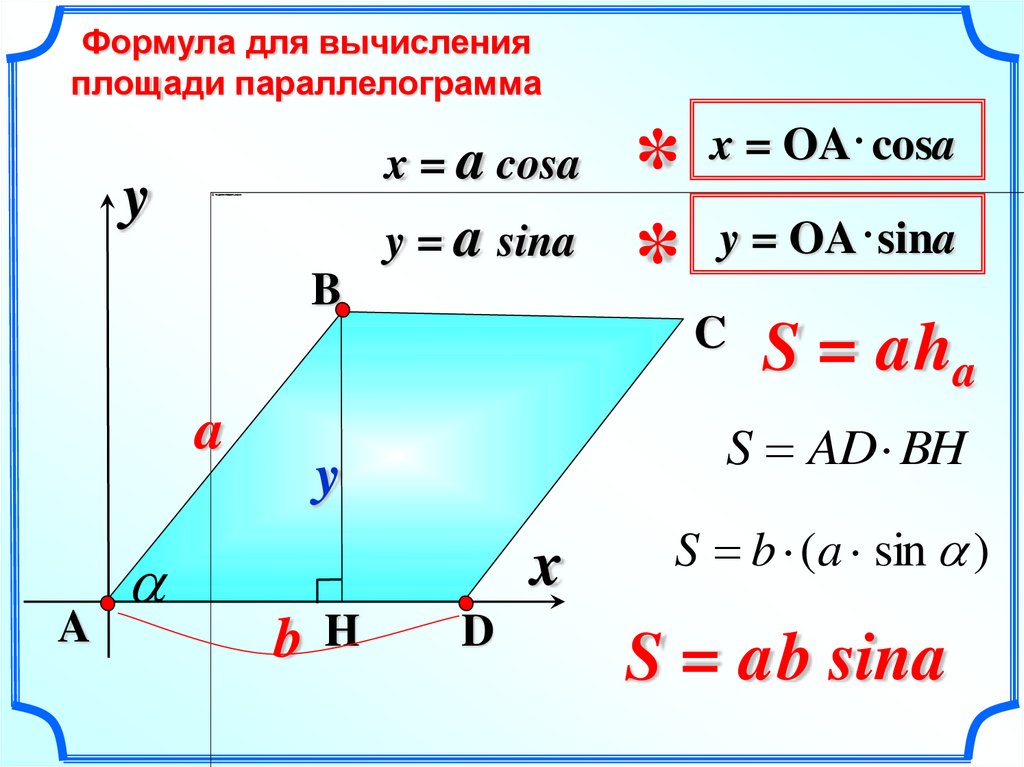
Формула для вычисления
площади параллелограмма
x = a cosa
y
y = a sina
B
*
*
x = OA cosa
y = OA sina
C
a
A
S AD BH
y
x
bH
S = aha
D
S b (a sin )
S = ab sina

26.

B
53
10
C
1200
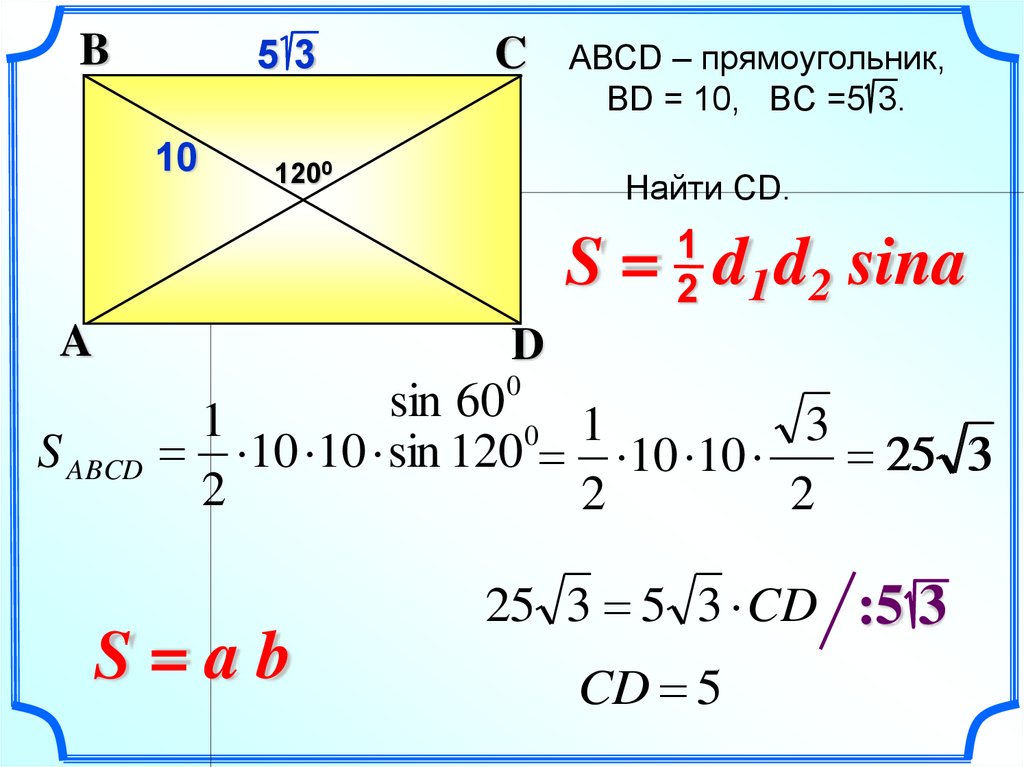
АВСD – прямоугольник,
ВD = 10, BC =5 3.
Найти CD.
1
2
S = d1 d2 sina
A
D
0
S ABCD
sin 60
1
3
0 1
10 10 sin 120 10 10
25 3
2
2
2
S=ab
25 3 5 3 CD :5 3
CD 5

27.

SABCD= 8 2 см2. Найти сторону ромба.
B
450
?
S=
A
C
2
a sina
8 2 а sin 45
2
0
2
8 2 а
2
2
а 16
2
D
а 4
:
2
2
AB 4

28.

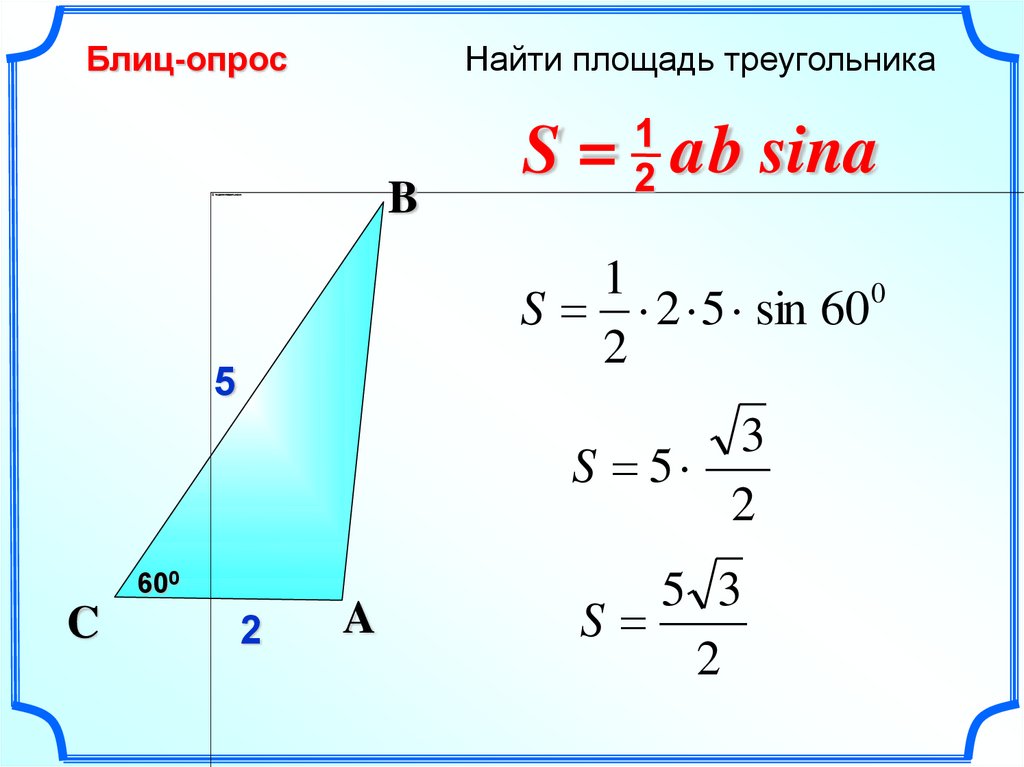
Блиц-опрос
Найти площадь треугольника
B
1
2
S = ab sina
1
0
S 2 5 sin 60
2
5
3
S 5
2
600
C
2
A
5 3
S
2

29.

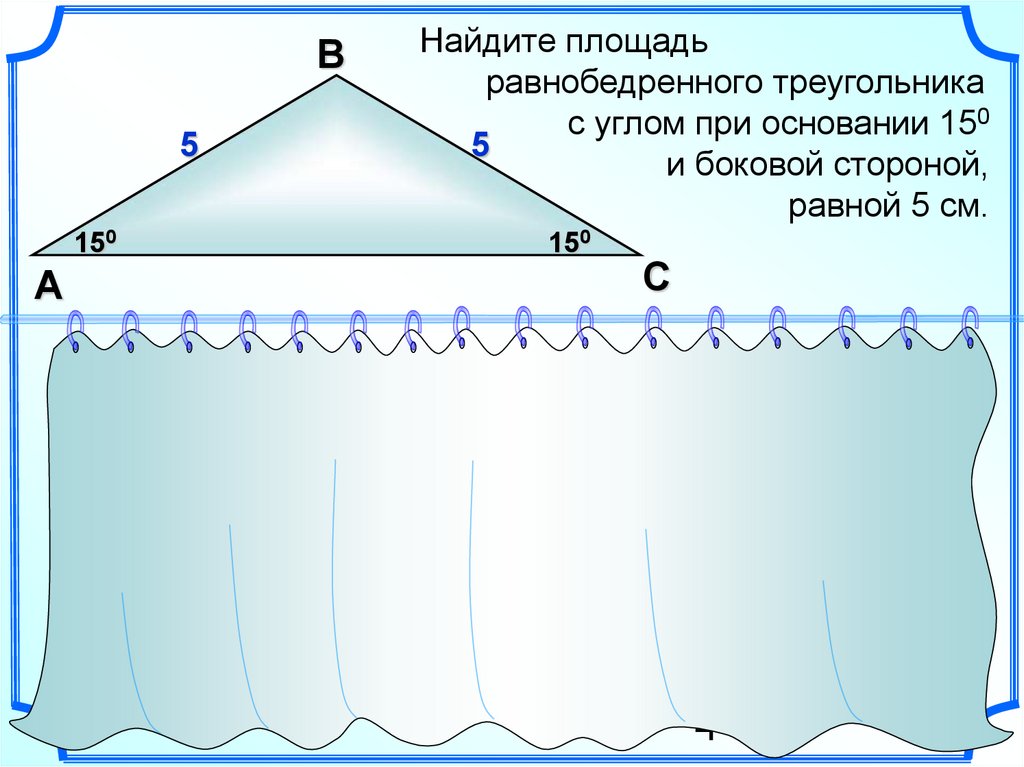
Найдите площадь
равнобедренного треугольника
с углом при основании 150
5
и боковой стороной,
равной 5 см.
В
5
150
150
A
С
1
2
S = ab sina
1
25
25 1 25
S 5 5 sin 150
sin 30
2
2
2 2 4
1
2
6 (см )
4