Похожие презентации:
Обратные тригонометрические функции
1.
2.
Обратныетригонометрические функции
у=arcctgx
у=arcsinx
график
график
у=arccosx
график
у=arctgx
график
3.
2Определение
0
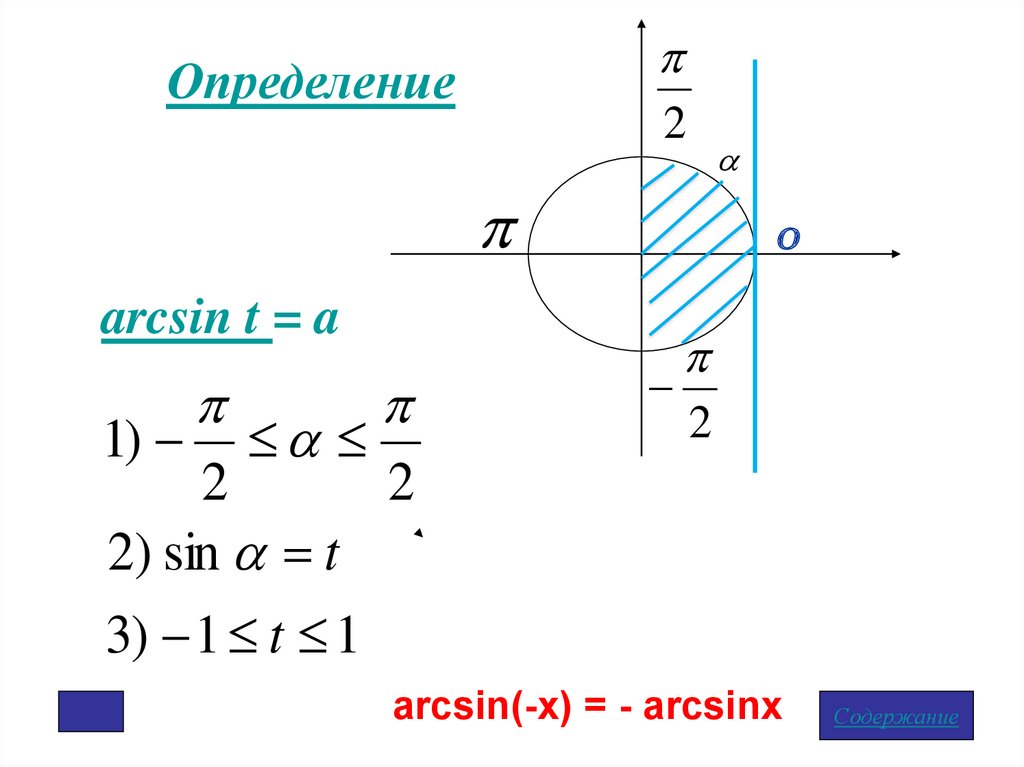
arcsin t = a
1)
2
2
2) sin t
3) 1 t 1
2
arcsin(-x) = - arcsinx
Содержание
4.
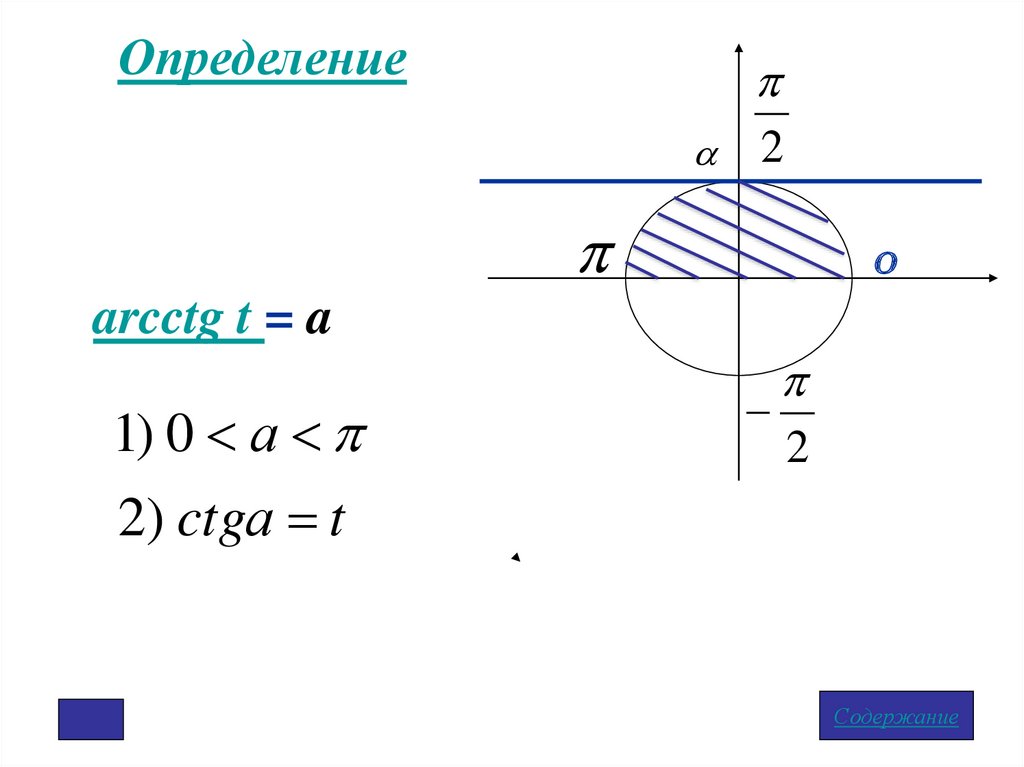
Определение2
0
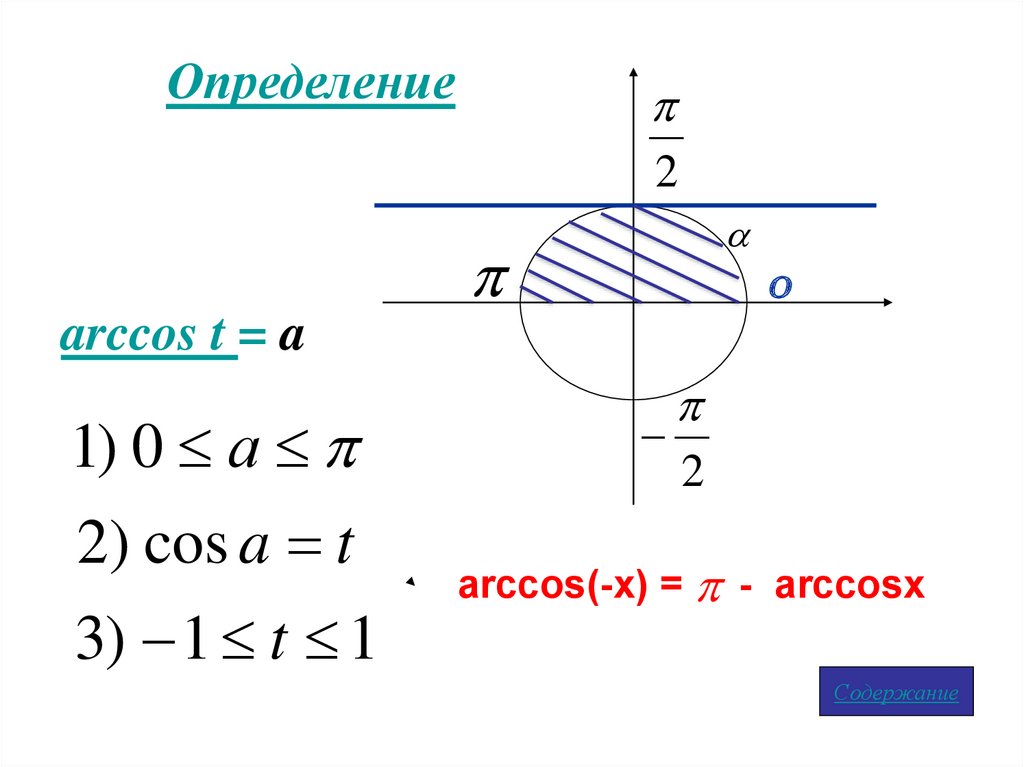
arccos t = a
1) 0 а
2) cos a t
3) 1 t 1
2
arccos(-x) = - arccosx
Содержание
5.
2Определение
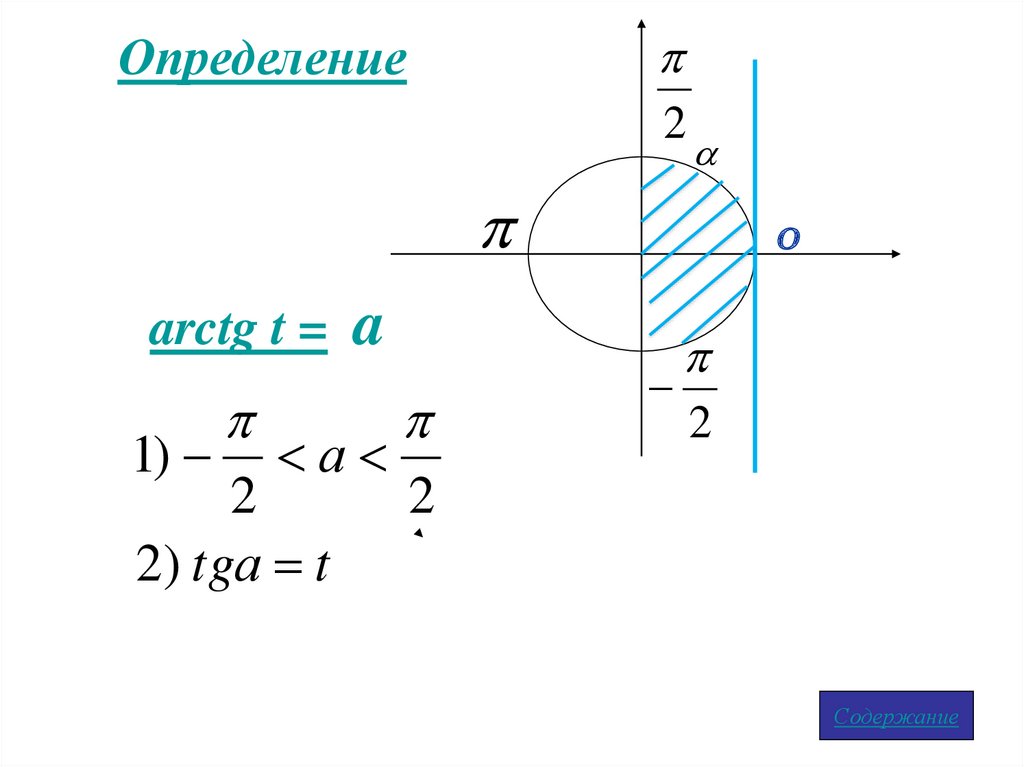
arctg t =
1)
a
а
2
2) tgа t
0
2
2
Содержание
6.
Определение2
0
arcctg t = a
1) 0 а
2
2) ctgа t
Содержание
7.
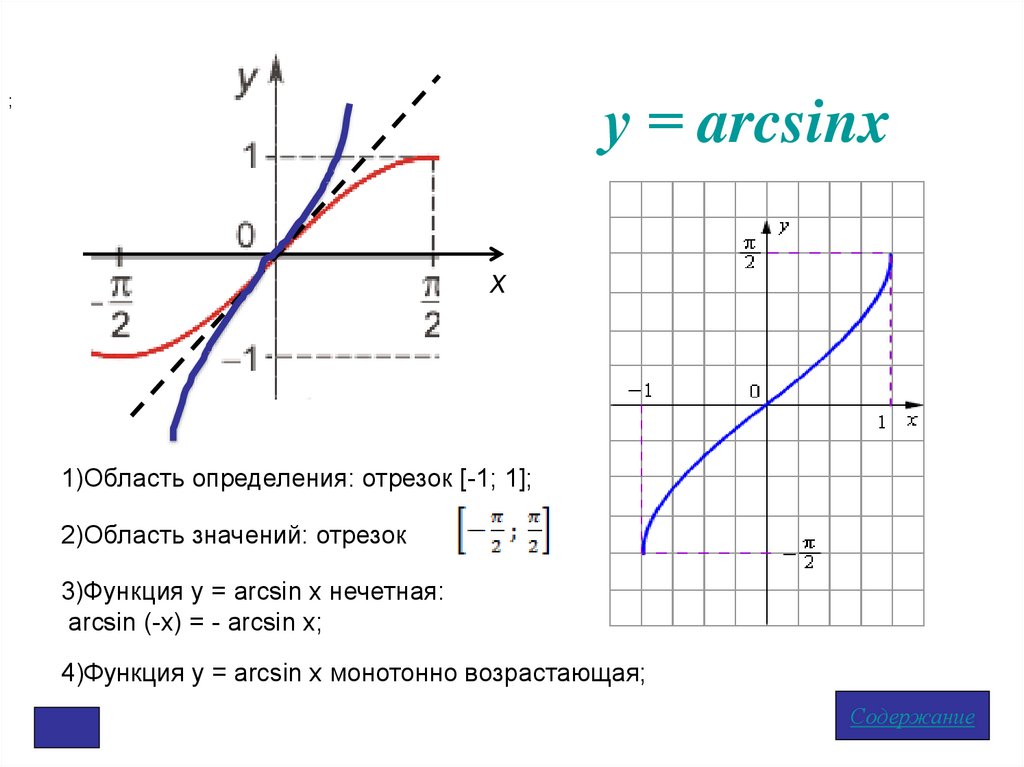
у = arcsinx;
х
1)Область определения: отрезок [-1; 1];
2)Область значений: отрезок
3)Функция у = arcsin x нечетная:
arcsin (-x) = - arcsin x;
4)Функция у = arcsin x монотонно возрастающая;
Содержание
8.
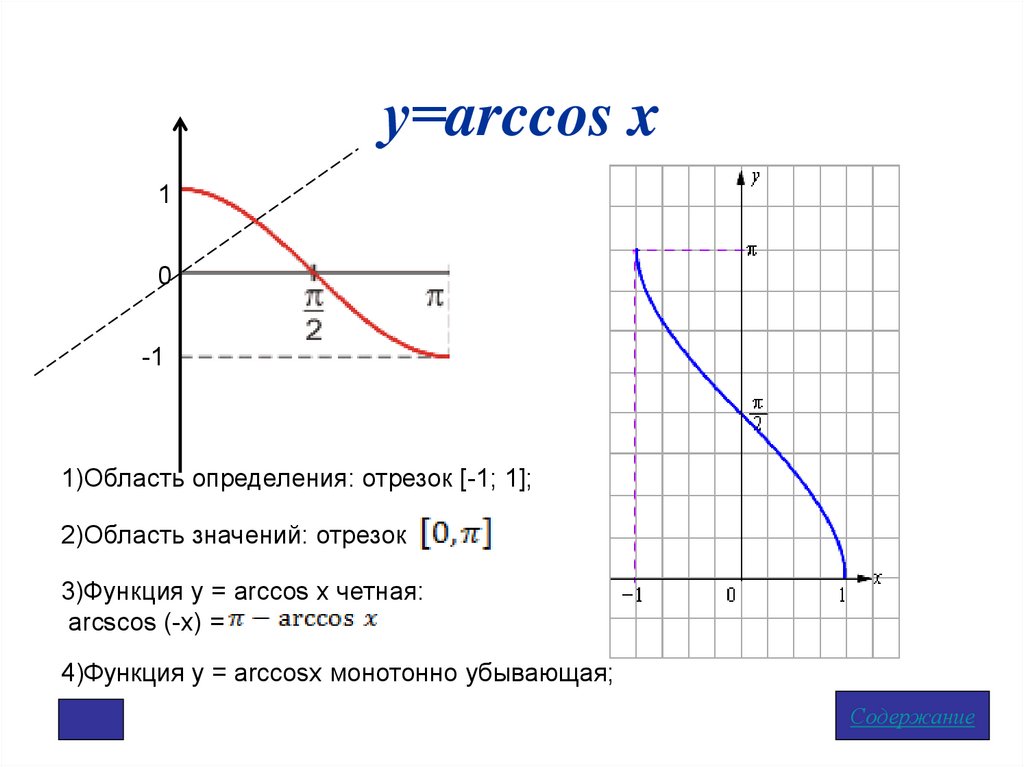
у=arccos x1
0
-1
1)Область определения: отрезок [-1; 1];
2)Область значений: отрезок
3)Функция у = arcсos x четная:
arcscos (-x) =
4)Функция у = arcсosx монотонно убывающая;
Содержание
9.
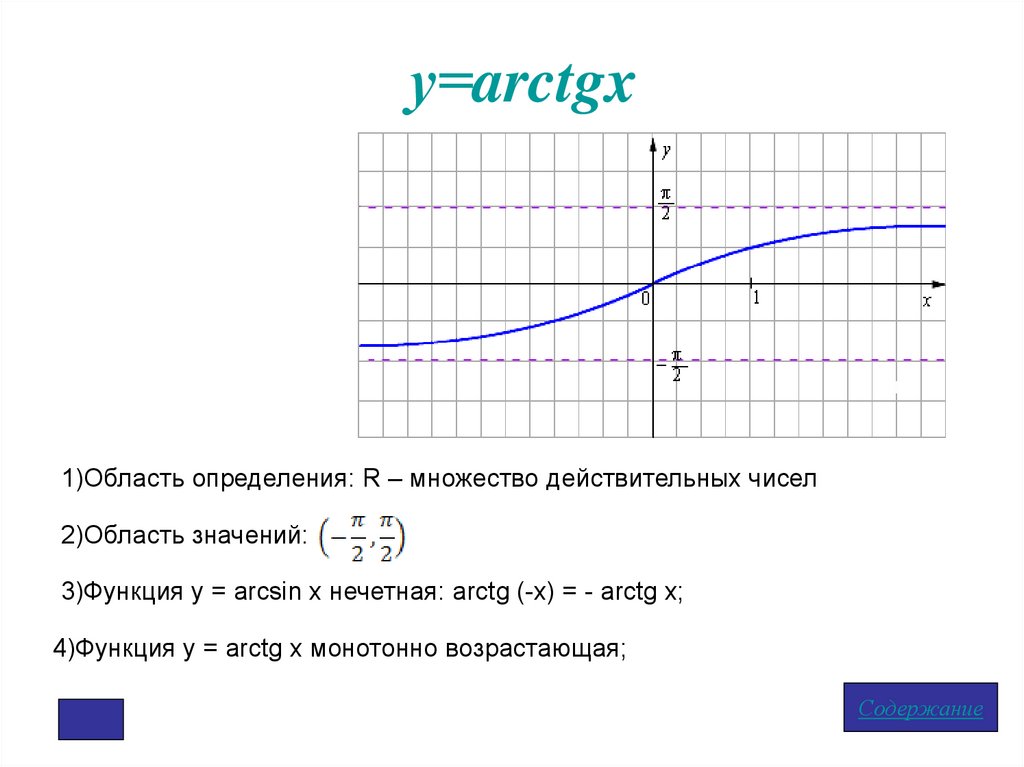
у=arctgx1)Область определения: R – множество действительных чисел
2)Область значений:
3)Функция у = arcsin x нечетная: arctg (-x) = - arctg x;
4)Функция у = arctg x монотонно возрастающая;
Содержание
10.
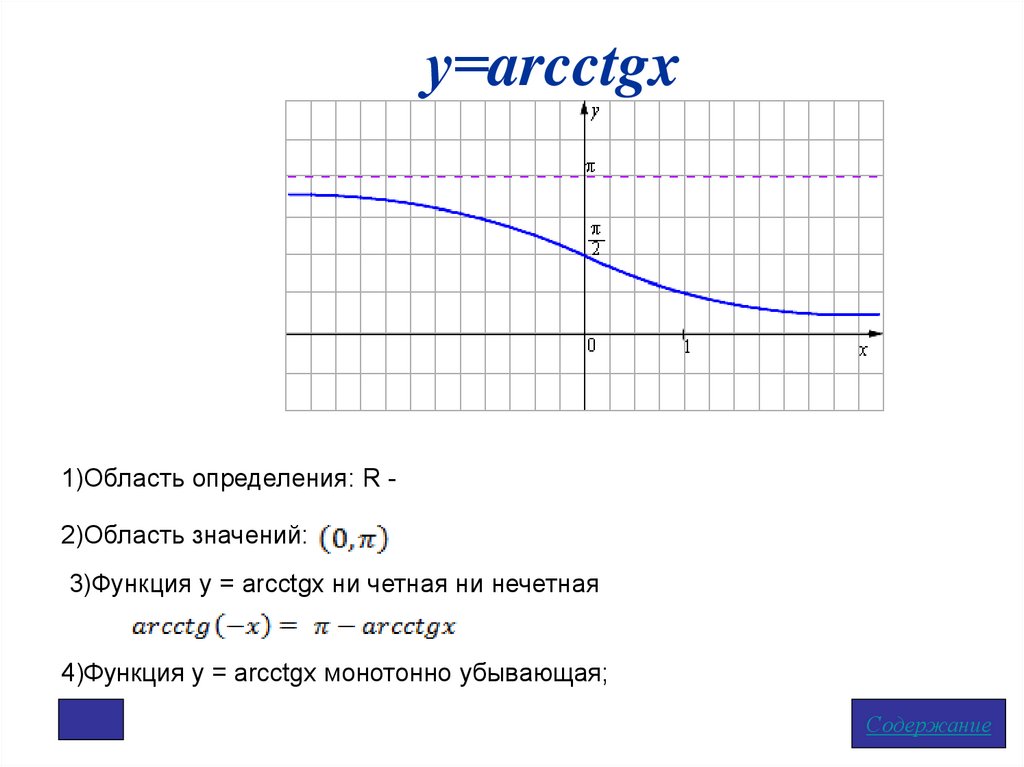
у=arcctgx1)Область определения: R 2)Область значений:
3)Функция у = arcctgх ни четная ни нечетная
4)Функция у = arcсtgx монотонно убывающая;
Содержание
11.
Свойства аркфункцийcos(arccos x) x,
arccos(cos x) x, x 1;1
sin(arcsin x) x,
arcsin(sin x) x, x 1;1
tg (arctgx) x
arctg (tgx) x,
ctg (arcctgx) x
arcctg (ctgx) x.



 Математика
Математика








