Похожие презентации:
Обратные тригонометрические функции и их свойства
1.
Обратные тригонометрическиефункции и их свойства
2.
Содержание• Функция y = arcsin x и ее свойства
• Функция y = arccos x и ее свойства
• Функция y = arctg x и ее свойства
• Функция y = arcctg x и ее свойства
3.
Функция y=arcsinx и ее свойстваЕсли |а| ≤ 1, то arcsin а – это такое число
из отрезка [-π/2;π/2], синус которого
равен а.
Если |а| ≤ 1, то
arcsin а = t
sin t = а,
-π/2 ≤ t ≤ π/2;
sin (arcsin a) = a
4.
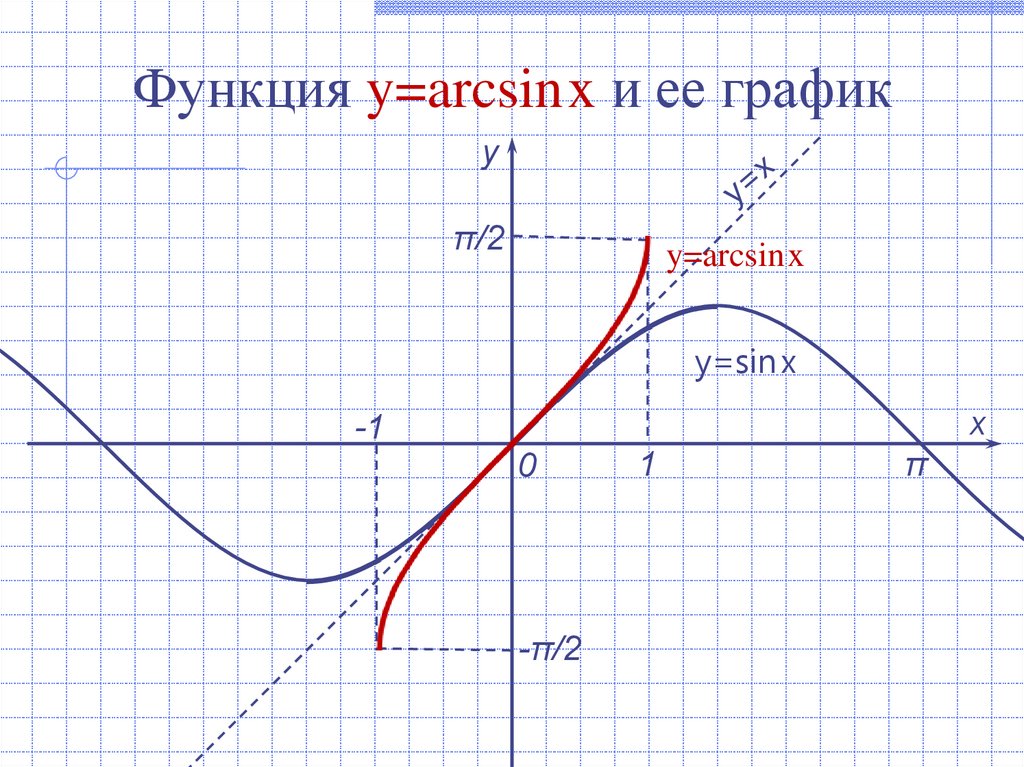
Функция y=arcsinx и ее графику
π/2
y=arcsinx
y=sin x
х
-1
0
-π/2
1
π
5.
Функция y=arcsinx и ее свойства1. D(y) = [-1; 1].
2. E(y) = [-π/2; π/2].
3. arcsin (-x) = - arcsin x – функция
нечетная.
4. Функция возрастает на [-1; 1].
5. Функция непрерывна.
6.
Функция y=arccos x и ее свойстваЕсли |а| ≤ 1, то arccos а – это такое число
из отрезка [0; π], косинус которого равен
а.
Если |а| ≤ 1, то
arccos а = t
cos t = а,
0 ≤ t ≤ π;
cos (arccos a) = a
arccos (-a) = π – arccos a, где -1 ≤ а ≤ 1
7.
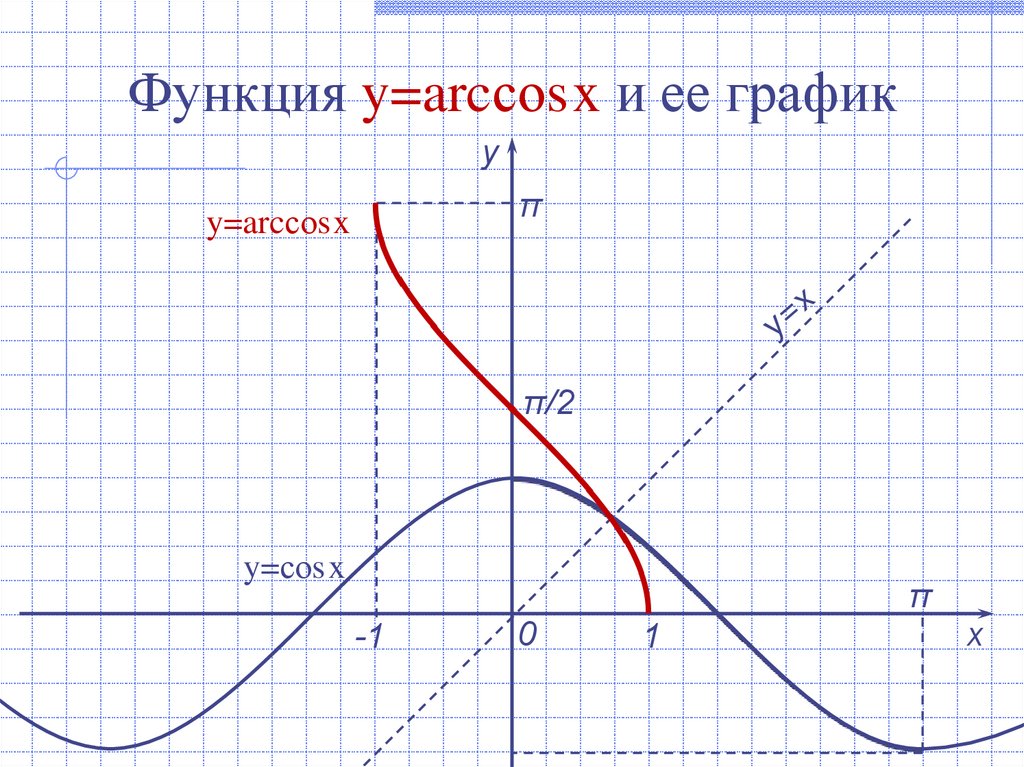
Функция y=arcсоsx и ее графику
π
y=arcсоsx
π/2
y=соsx
π
-1
0
1
х
8.
Функция y=arccosx и ее свойства1. D(y) = [-1; 1].
2. E(y) = [0; π].
3. Функция не является ни четной, ни
нечетной.
4. Функция убывает на [-1; 1].
5. Функция непрерывна.
9.
Функция y=arctgx и ее свойстваarctg а – это такое число из интервала (-π/2; π/2),
тангенс которого равен а.
arctg а = t
tg t = а,
-π/2 < t < π/2;
tg (arctg a) = a
10.
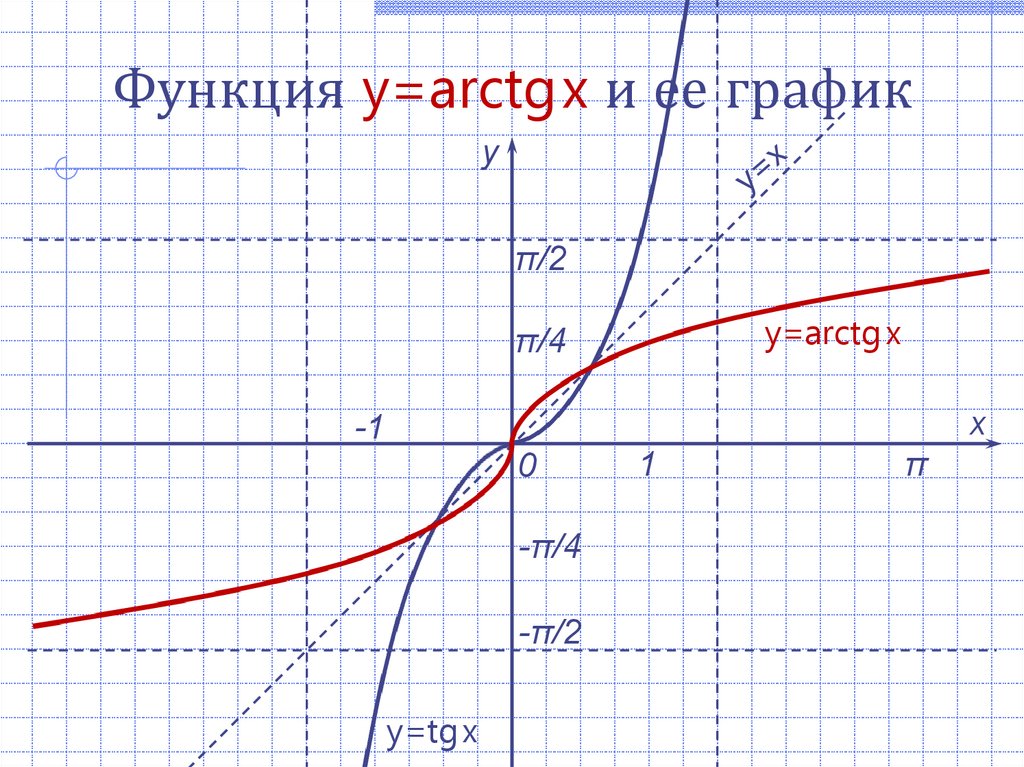
Функция y=arctgx и ее графику
π/2
y=arctg x
π/4
х
-1
0
-π/4
-π/2
y=tg x
1
π
11.
Функция y=arctgx и ее свойства1. D(y) = (- ; + ).
2. E(y) = (-π/2; π/2).
3. arctg (-x) = - arctg x – функция нечетная.
4. Функция возрастает на (- ; + ).
5. Функция непрерывна.
12.
Функция y=arcсtgx и ее свойстваarcсtg а – это такое число из интервала (0; π),
котангенс которого равен а.
arcсtg а = t
сtg t = а,
0 < t < π;
сtg (arcсtg a) = a
arcctg (-a) = π – arcctg a
13.
Функция y=arcсtgx и ее графику
π
y=сtg x
y=arcсtg x
π/2
-π
-π/2
0
π/2
π
х
14.
Функция y=arcсtgx и ее свойства1. D(y) = (- ; + ).
2. E(y) = (0; π).
3. Функция не является ни четной, ни
нечетной.
4. Функция убывает на (- ; + ).
5. Функция непрерывна.











 Математика
Математика








