Похожие презентации:
Оценка сложных систем в условиях стохастической неопределенности. (Лекция 10)
1.
Оценка сложных системв условиях стохастической
неопределенности
Лекция 10
2.
Учебные вопросы:10.1 Принятие решений в условиях риска
10.2 Принятие решений на основе функции полезности
Литература:
1 Анфилатов, В.С. Системный анализ в управлении: Уч. пособие:
/В.С. Анфилатов, А.А. Емельянов, А.А. Кукушкин. – М.: Финансы и
статистика, 2006. - 109-130 с. – ISBN 5-279-02435-X
2 Соловьев, Н.А. Основы теории принятия решений для
программистов: учебное пособие: /Н.А. Соловьев, Е.Н. Чернопрудова,
Д.А. Лесовой – Оренбург: ООО ИПК «Университет», 2012. – С. 32-47.
ISBN 978-5-4417-0092-4.
3.
10.1 Принятие решений в условиях риска4.
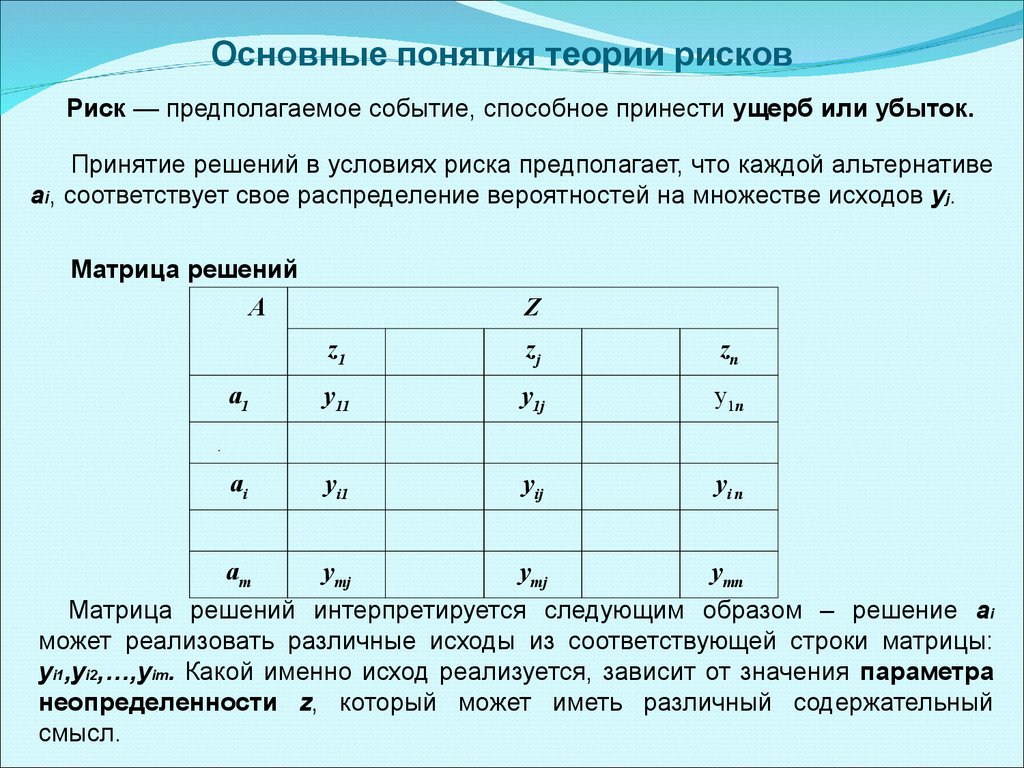
Основные понятия теории рисковРиск — предполагаемое событие, способное принести ущерб или убыток.
Принятие решений в условиях риска предполагает, что каждой альтернативе
аi, соответствует свое распределение вероятностей на множестве исходов уj.
Матрица решений
А
Z
z1
zj
zn
а1
у11
у1j
у1n
ai
уi1
уij
уi n
аm
уmj
уmj
уmn
.
Матрица решений интерпретируется следующим образом – решение аi
может реализовать различные исходы из соответствующей строки матрицы:
уi1,yi2,…,yim. Какой именно исход реализуется, зависит от значения параметра
неопределенности z, который может иметь различный содержательный
смысл.
5.
Принятие решений в условиях рискаЗадачу принятия решений в условиях риска можно представить в форме
функции риска
Y = F(a,z).
Каждому состоянию среды zj соответствует вероятность его наступления p(zj)
n
p ( z j ) pi ( y j (ai ))
i 1
где pi(yj(ai)) – вероятность наступления исхода yj при выборе альтернативы аi .
Тогда существует функционал K: Y Z R и задача принятия решений
сводится задаче оптимизации
K (a, z ) opt
a A
При многократно реализуемым исходам используется МОЖ критерия вида
K (a ) K (a, z ) opt
a A
6.
Задача о замене вратаряУсловие задачи. На последних минутах хоккейного матча при ничейном счете тренер
должен принять решение о замене вратаря 6-м полевым игроком.
Имеется информация, что в аналогичных условиях предыдущих встреч замена вратаря
в 1/6 части случаев привела к выигрышу, в половине (1/2) – к ничьей и в 1/3 – к поражению.
Если же вратарь не менялся, то в 7/8 случаев встреча заканчивалась в ничью, а в 1/8
части случаев команда проигрывала .
Решение
Цель (критерий) принятия решений - максимальное число ожидаемых очков.
Матрица решений (а1 –вратаря сменить, а2 – вратаря не менять)
А
Z
z1
z2
z3
z4
z5
z6
а1
B
H
П
В
Н
П
a2
Н
Н
Н
П
П
П
где В – выигрыш, приносящий 2 очка;
Н – ничья (1 очко);
П – поражение (0 очков).
7.
Задача о замене вратаря (продолжение)Расчет параметра неопределенности:
z1: a1 B, a2 H, p(z1) = 1/6 7/8 = 7/48
z2: a1 Н, a2 H, p(z2) = 1/2 7/8 = 7/16
z3: a1 П, a2 H, p(z3) = 1/3 7/8 = 7/24
z4: a1 B, a2 П, p(z4) = 1/6 1/8 = 1/48
z5: a1 Н, a2 П, p(z5) = 1/2 1/8 = 1/16
z6: a1 П, a2 П, p(z6) = 1/3 1/8 = 1/24
Матрица рисков примет вид
А
Z
z1 (7/48)
z2(7/16)
z3(7/24)
z4(1/48)
z5(1/16)
z6(1/24)
а1
B(2)
H(1)
П(0)
B(2)
H(1)
П(0)
а2
Н(1)
Н(1)
Н(1)
П(0)
П(0)
П(0)
K (a1 , z ) 2 (7 / 48) 1 (7 / 16) 2 (1 / 48) 1 (1 / 16) 5 / 6
K (a2 , z ) 1 (7 / 48) 1 (7 / 16) 1 (1 / 24) 7 / 8
K (a 2 , z ) K (a1 , z )
Результат решения. Руководствуясь критерием числа ожидаемых очков,
принимается решение вратаря не менять.
8.
10.2 Принятие решений на основе функцииполезности
9.
Основные понятия теории полезностиПолезность – это действительное число, приписываемое исходу операции,
которое характеризует его предпочтительность по сравнению с другими
альтернативами относительно цели.
Доказано существование функции полезности, для которой предпочтения
ЛПР формулируются в виде аксиом:
Аксиома 1 – измеримость (каждому альтернативному исходу yk может
быть поставлено неотрицательное действительное число рi, (0 рi 1),
рассматриваемое как мера относительной полезности исхода.
Аксиома 2 – сравнимость (любые два исхода (альтернативы) сравнимы:
либо один исход предпочтительней другого, либо они эквивалентны).
Аксиома 3 – транзитивность (соотношения предпочтения исходов
транзитивны, если исход ai предпочтительнее аj , а исход аj предпочтительнее
аk, то исход ai также предпочтительнее аk).
Аксиома 4 – коммутативность (предпочтение исхода ai исходу аj не
зависит от порядка, в котором они представлены).
Аксиома 5 – независимость (если исход ai предпочтительнее исхода аj и,
кроме того, существует исход аk , который не оценивается относительно
исходов ai и аj , то смесь исходов ai и аk предпочтительнее смеси исходов аj и аk.
10.
Функция полезностиФункция полезности представляет собой числовую функцию F(a), определенную на
множестве альтернатив A={ai) так, что F(ai) = F(aj), когда альтернативы ai и aj
неразличимы; F(ai) > F(aj), когда альтернатива ai предпочтительнее aj .
В вероятностных операций функция полезности носит случайный характер и
определяется через F(y) – функцию полезности на множестве исходов у, т.е. критерий
выбора (решения) примет вид
K ( ai ) max M ai F ( y )
ai
В соответствии с этим критерием оптимальной системой в условиях стохастической
неопределенности считается система с максимальным значением математического
ожидания функции полезности на множестве исходов операции.
При исходах с дискретными значениями показателей
K ai
m
P( y
k 1
k
/ a i ) F y k , i 1, n
где y k ( k 1, m) – значения частного показателя;
р y k / ai – условная вероятность появления значения показателя;
F ( yk )
– функция полезности значения показателя;
При исходах с непрерывными значениями показателей
K (ai )
f ( y / a ) F ( y )dy
i
Rg
11.
Условия оценки альтернативai
a1
a2
yk
y1
y2
р ( yk / ai )
р ( y1 / a1 )
р ( y 2 / a1 )
ym
y1
y2
р ( ym / a1 ) F ( y m )
р ( y1 / a 2 )
р( y 2 / a2 )
F ( y1 )
F ( y2 )
ym
р ( y m / a2 )
F ( ym )
F ( yk )
F ( y1 )
F ( y2 )
K ai
K a1
K a2
12.
Определение полезностиОпределение полезности как меры оценки того или иного исхода операции
представляет сложную задачу, точные методы решения которой пока не
найдены. Все известные способы определения функции полезности носят
приближенный характер и относятся к экспертному оцениванию или
аппроксимации.
F (a k )
F (5)
F ( 4)
F ( 2) F (3)
1
2
3
4
5
Рисунок – Функция полезности на основе предпочтений ЛПР
ak
13.
Определение полезности (продолжение)F (a )
1
1
2
3
0
a min
a0
a max
A
Рисунок – Аппроксимация функции полезности
1 – одноступенчатое, 2 – косинусоидальное, 3 – треугольное
14.
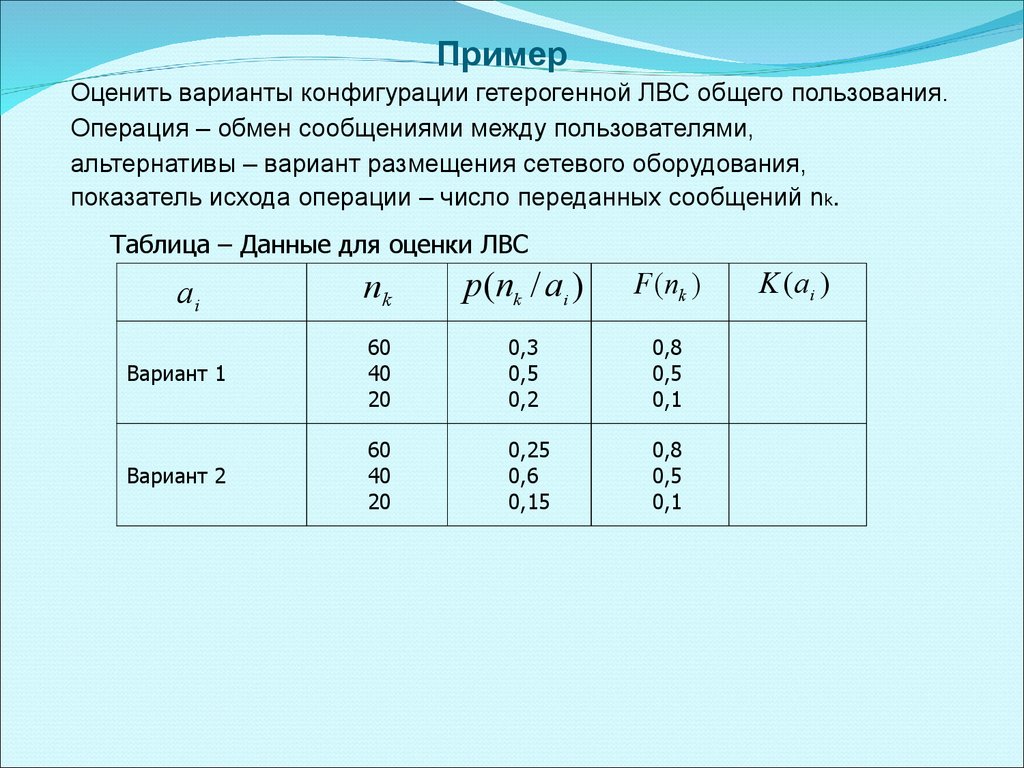
ПримерОценить варианты конфигурации гетерогенной ЛВС общего пользования.
Операция – обмен сообщениями между пользователями,
альтернативы – вариант размещения сетевого оборудования,
показатель исхода операции – число переданных сообщений nk.
Таблица – Данные для оценки ЛВС
nk
р(nk / ai )
F (nk )
Вариант 1
60
40
20
0,3
0,5
0,2
0,8
0,5
0,1
Вариант 2
60
40
20
0,25
0,6
0,15
0,8
0,5
0,1
ai
K (ai )
15.
Критерии оценки системK (a1 ) 1 / 3 (0,3 0,8 0,5 0,5 0,2 0,1) 0,17
K (a 2 ) 1 / 3 (0,25 0,8 0,6 0,5 0,15 0,1) 0,172
K опт max K (ai ) K (a 2 ) 0,172
В качестве оптимальной системы должен быть признан вариант 2.
Кроме оптимизации «в среднем» в вероятностных операциях используются и
другие критерии оценки систем:
- максимум вероятности случайного события;
- максимум вероятностной гарантии достижения результата не ниже
требуемого уровня;
- максимум среднего квадрата уклонения результата от требуемого;
- минимум дисперсии результата;
- минимум среднего (байесовского) риска (минимум средних потерь).
16.
Вопросы и задания для самоконтроляЧто представляет собой матрица решений?
Что такое полезность исхода операции?
Каким математическим выражением можно представить критерий
оптимальности для вероятностных операций?
Сформулируйте аксиому измеримости?
В какой аксиоме предпочтение исхода ai исходу аj не зависит от
порядка, в котором они представлены.
Сформулируйте аксиому независимости.
Что представляет собой функция полезности?
Как определить функцию полезности?
Какие критерии оценки систем используются в вероятностных
операциях?














 Менеджмент
Менеджмент Программное обеспечение
Программное обеспечение








