Похожие презентации:
Нахождение угла между двумя прямыми в пространстве
1. Нахождение угла между двумя прямыми в пространстве
2. Цели обучения
11.4.2 - находить угол между прямыми(по заданным уравнениям прямых);
3. Цели урока
• Уметь находить угла между двумя прямымив пространстве
4.
Прямая в пространстве• Каноническое уравнение прямой
• Параметрическое уравнение прямой
• Угол между двумя прямыми
5.
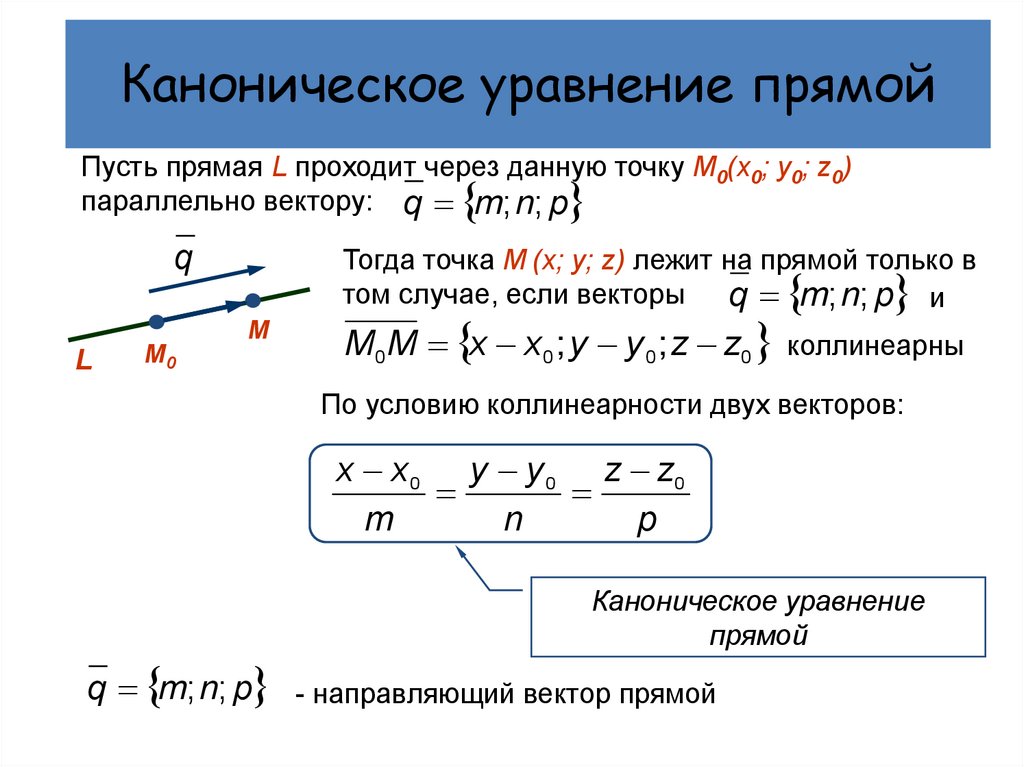
Каноническое уравнение прямойПусть прямая L проходит через данную точку М0(x0; y0; z0)
параллельно вектору: q m; n; p
Тогда точка М (x; y; z) лежит на прямой только в
том случае, если векторы
q m; n; p и
q
L
М0
М
M0M x x0 ; y y 0 ; z z0 коллинеарны
По условию коллинеарности двух векторов:
x x0 y y 0 z z0
m
n
p
Каноническое уравнение
прямой
q m; n; p - направляющий вектор прямой
6. Каноническое уравнение прямой
Каноническое уравнениеуравнение прямой
прямой
Каноническое
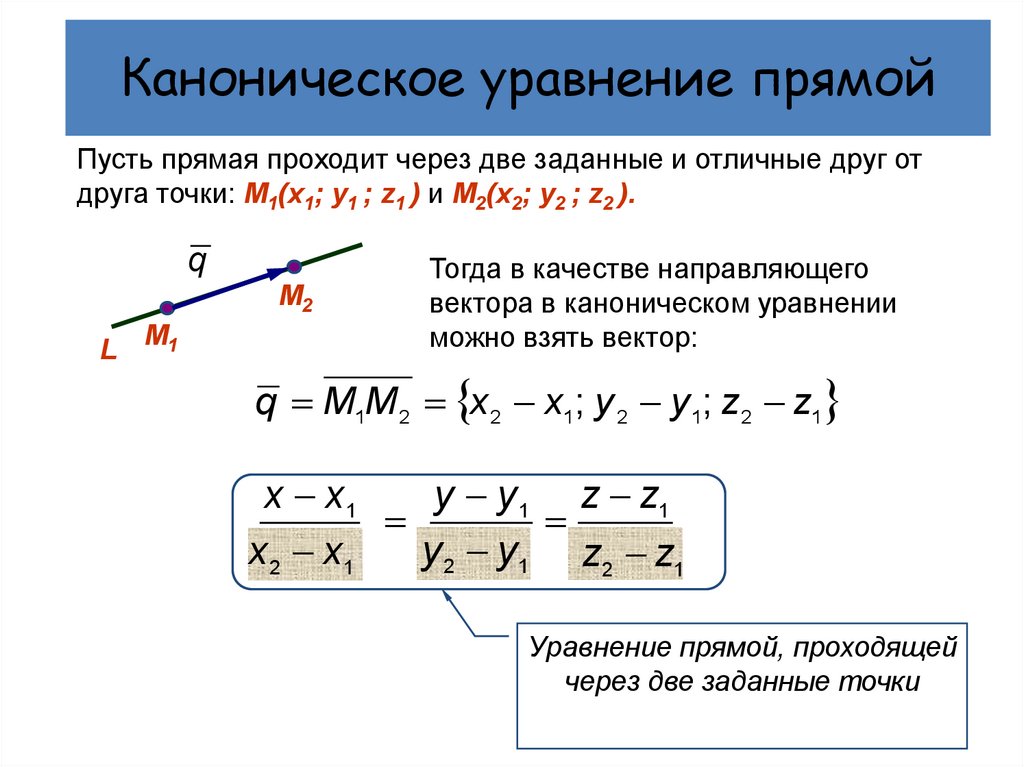
Пусть прямая проходит через две заданные и отличные друг от
друга точки: М1(х1; у1 ; z1 ) и М2(х2; у2 ; z2 ).
q
М2
L М1
Тогда в качестве направляющего
вектора в каноническом уравнении
можно взять вектор:
q M1M 2 x 2 x1; y 2 y 1; z2 z1
x x1
y y 1 z z1
y 2 n y1 z2 p z1
mx1
x2
Уравнение прямой, проходящей
через две заданные точки
7.
Параметрическое уравнение прямойПри решении многих практических задач используют
параметрическое уравнение прямой, которое получается из
канонического уравнения:
x x0 y y 0 z z0
t
m
n
p
x mt x 0
y nt y 0
z pt z
0
x x0
m t
y y
0
t
n
z z0 t
p
Параметрическое уравнение
прямой
8. Угол между прямыми
Угол между прямымиПусть две прямые заданы каноническими уравнениями:
x x 2 y y 2 z z2
L2 :
m2
n2
p2
x x1 y y 1 z z1
L1 :
m1
n1
p1
Углом между этими прямыми называется угол между
направляющими векторами к этим прямым.
q1 m1; n1; p1
q2 m2 ; n2 ; p2
cos
q2
q1
L1
L2
q1 q2
q1 q2
m1 m2 n1 n2 p1 p2
m12 n12 p12 m22 n22 p22
9. Пример:
Решение: Для решения этой задачи найдем направляющие векторы этихпрямых. Уравнение первой прямой задано в канонической форме, поэтому
направляющий вектор {3; 4; 5}. Преобразуем второе уравнение к
каноническому вид.
Получено уравнение второй прямой в канонической форме:
{-2; -1/3; 2/3} - направляющий вектор второй прямой.









 Математика
Математика








