Прямоугольник, ромб, квадрат. Осевая и центральная симметрии

1.

ПРЯМОУГОЛЬНИК
mathvideourok.moy.su

2.

Прямоугольник это
параллелограмм у которого все
углы прямые
СВОЙСТВА ПРЯМОУГОЛЬНИКА:
1.Противоположные
стороны равны.
2. Диагонали точкой
пересечения делятся
пополам

3.

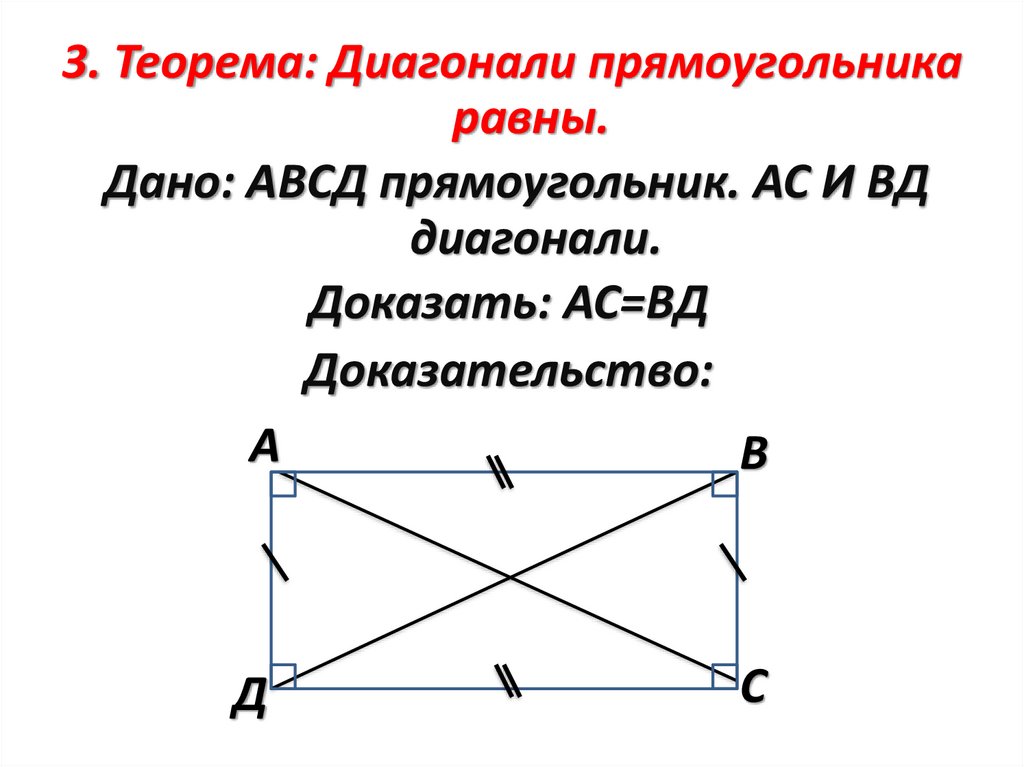
3. Теорема: Диагонали прямоугольника
равны.
Дано: АВСД прямоугольник. АС И ВД
диагонали.
Доказать: АС=ВД
Доказательство:
А
В
Д
С

4.

А
В
Д
С
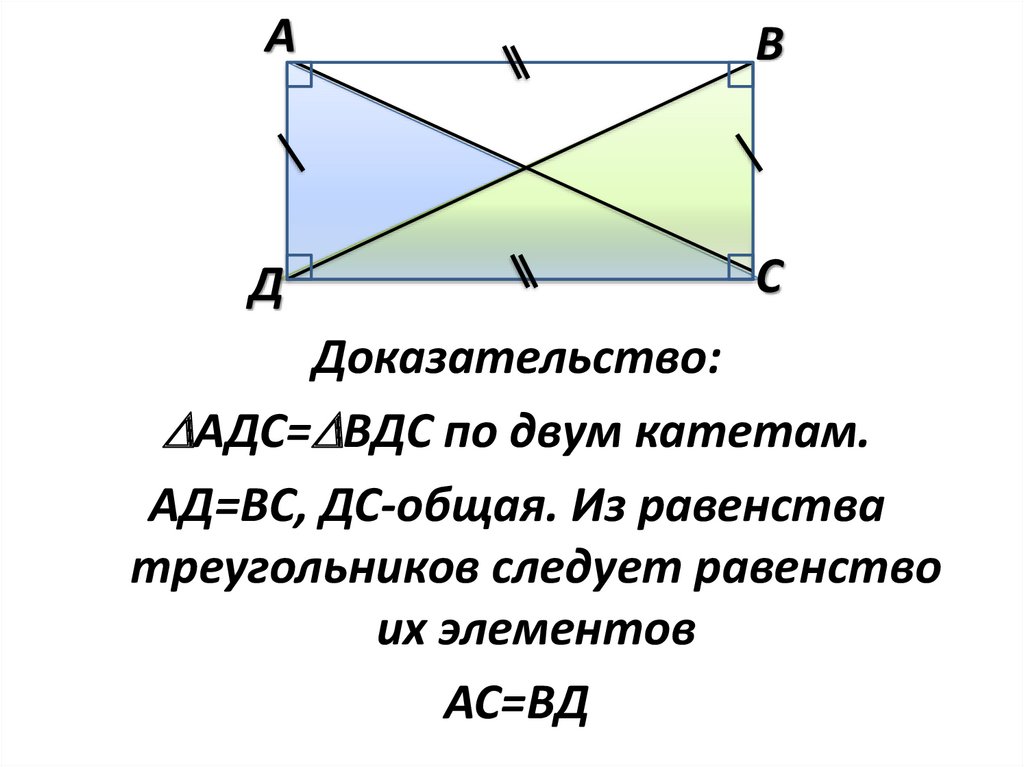
Доказательство:
АДС= ВДС по двум катетам.
АД=ВС, ДС-общая. Из равенства
треугольников следует равенство
их элементов
АС=ВД

5.

Теорема (Признак прямоугольника)
Если в параллелограмме диагонали
равны, то этот параллелограмм
прямоугольник.

6.

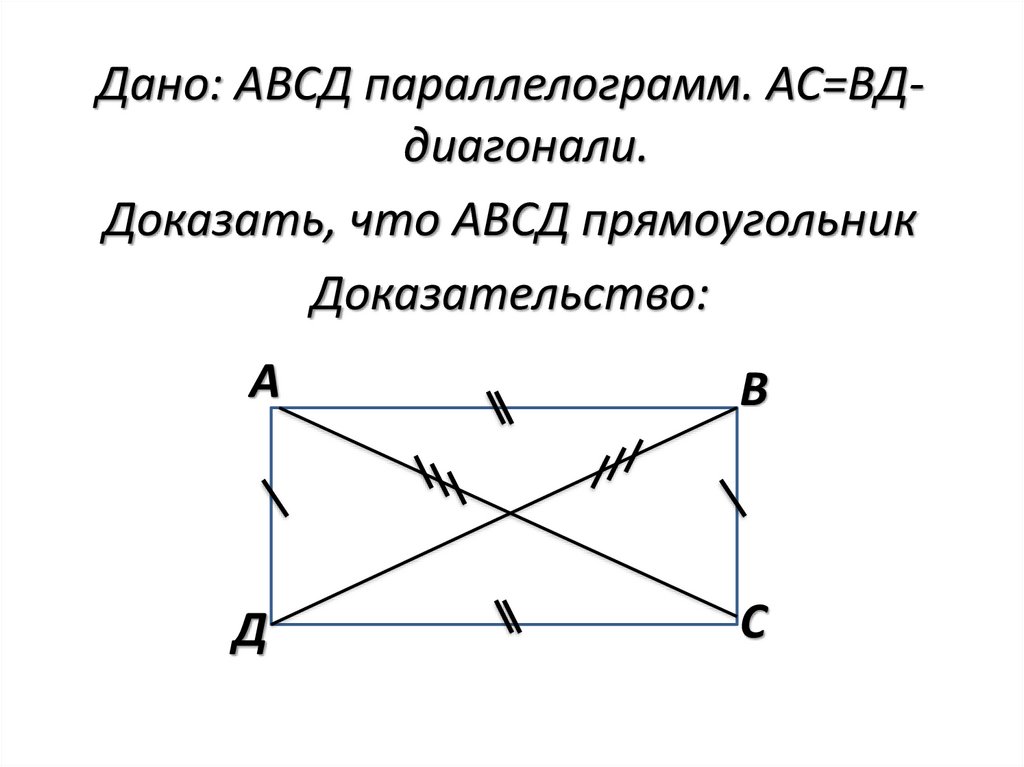
Дано: АВСД параллелограмм. АС=ВДдиагонали.
Доказать, что АВСД прямоугольник
Доказательство:
А
В
Д
С

7.

А
Д
В
3
4
1
2
С
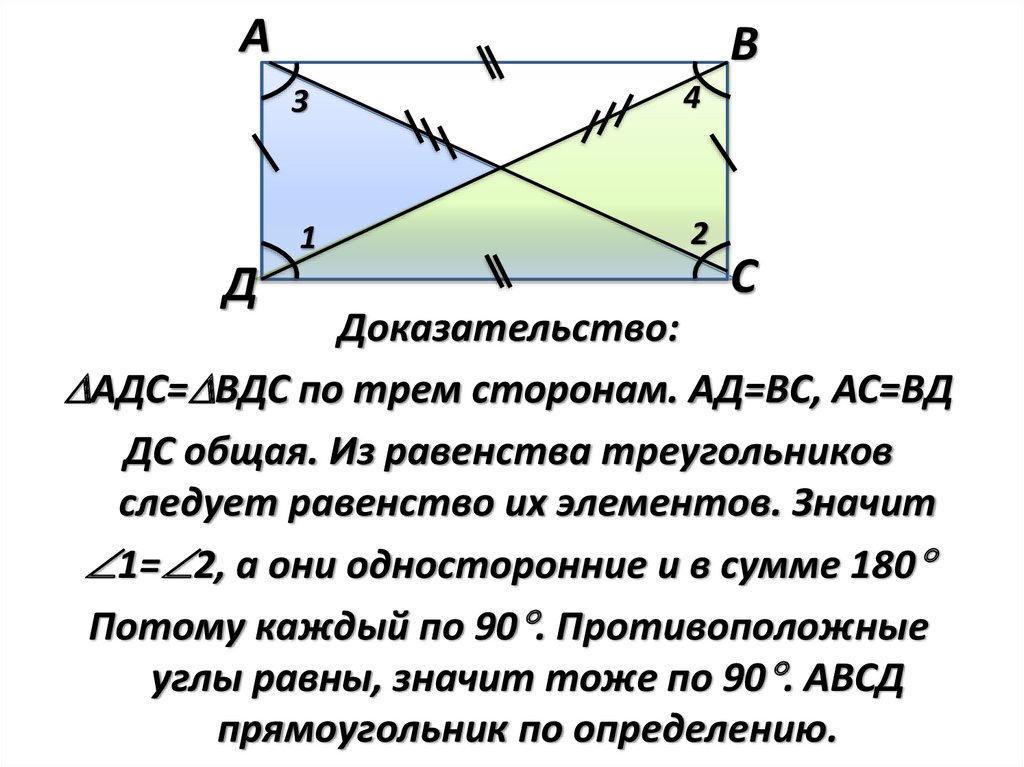
Доказательство:
АДС= ВДС по трем сторонам. АД=ВС, АС=ВД
ДС общая. Из равенства треугольников
следует равенство их элементов. Значит
1= 2, а они односторонние и в сумме 180
Потому каждый по 90 . Противоположные
углы равны, значит тоже по 90 . АВСД
прямоугольник по определению.

8.

РОМБ

9.

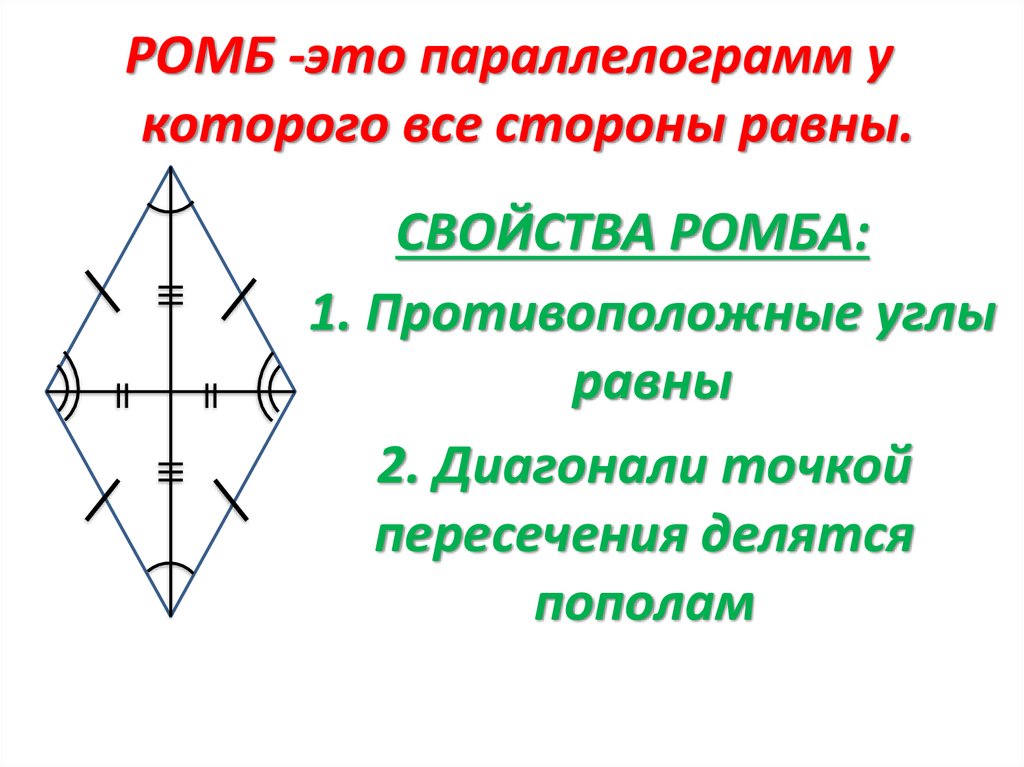
РОМБ -это параллелограмм у
которого все стороны равны.
СВОЙСТВА РОМБА:
1. Противоположные углы
равны
2. Диагонали точкой
пересечения делятся
пополам

10.

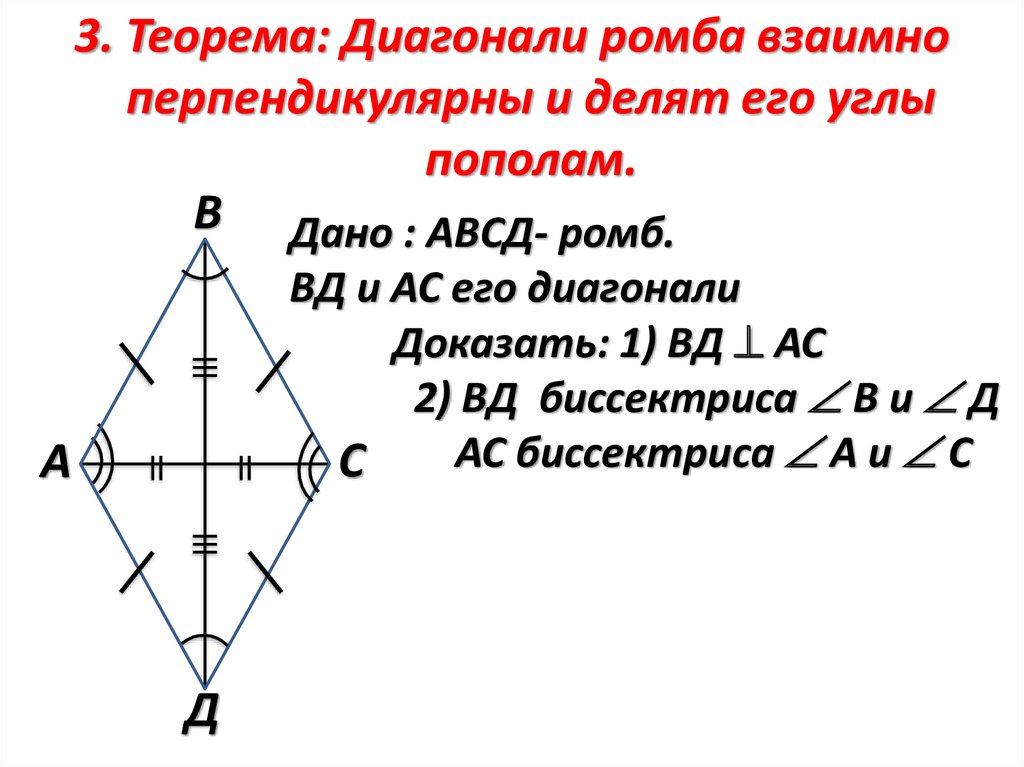
3. Теорема: Диагонали ромба взаимно
перпендикулярны и делят его углы
пополам.
В Дано : АВСД- ромб.
ВД и АС его диагонали
Доказать: 1) ВД АС
2) ВД биссектриса В и Д
АС биссектриса А и С
С
А
Д

11.

В
А
О
Д
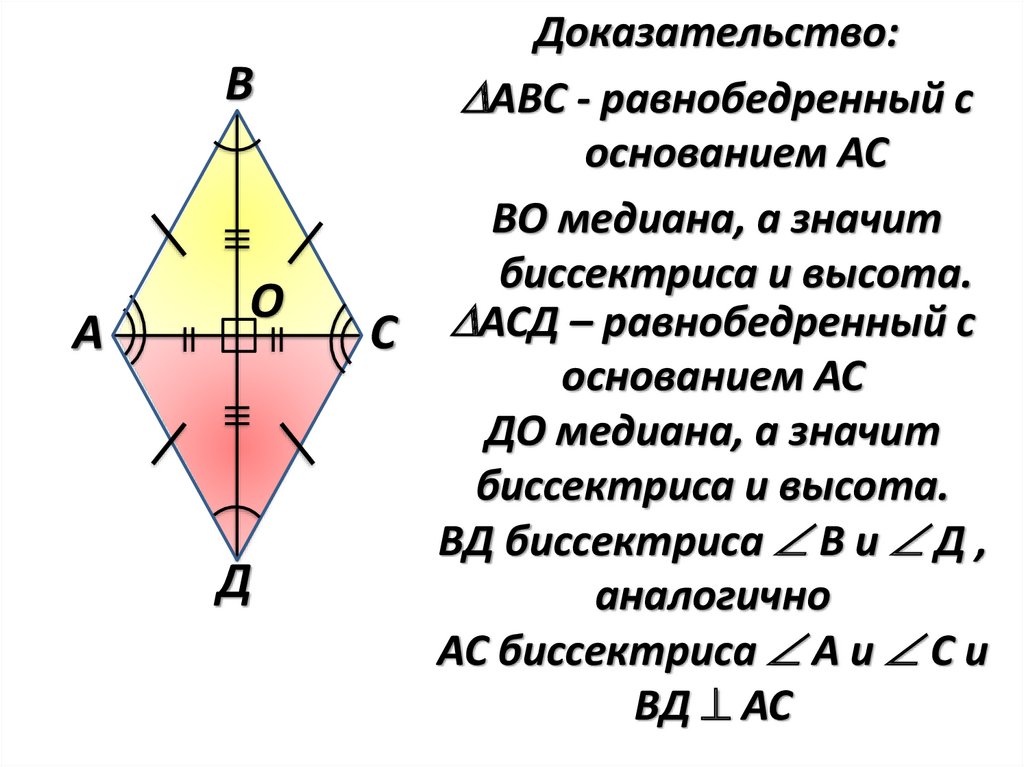
Доказательство:
АВС - равнобедренный с
основанием АС
ВО медиана, а значит
биссектриса и высота.
С АСД – равнобедренный с
основанием АС
ДО медиана, а значит
биссектриса и высота.
ВД биссектриса В и Д ,
аналогично
АС биссектриса А и С и
ВД АС

12.

КВАДРАТ

13.

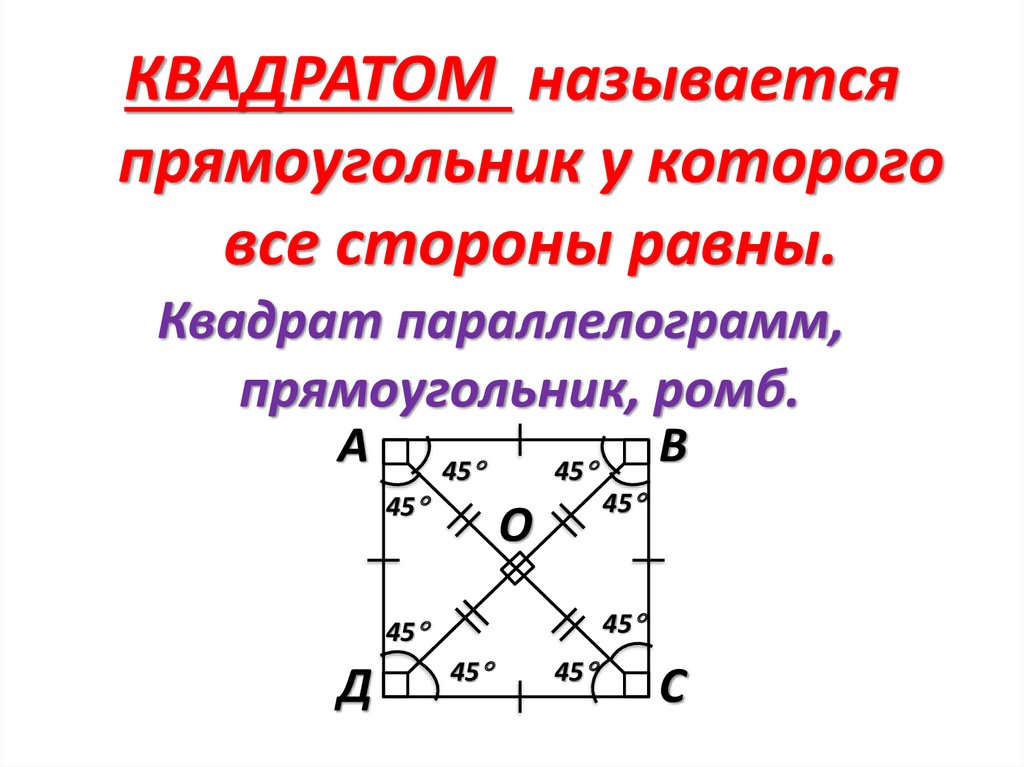
КВАДРАТОМ называется
прямоугольник у которого
все стороны равны.
Квадрат параллелограмм,
прямоугольник, ромб.
А
45
45
45
О
45
45
45
Д
В
45
45
С

14.

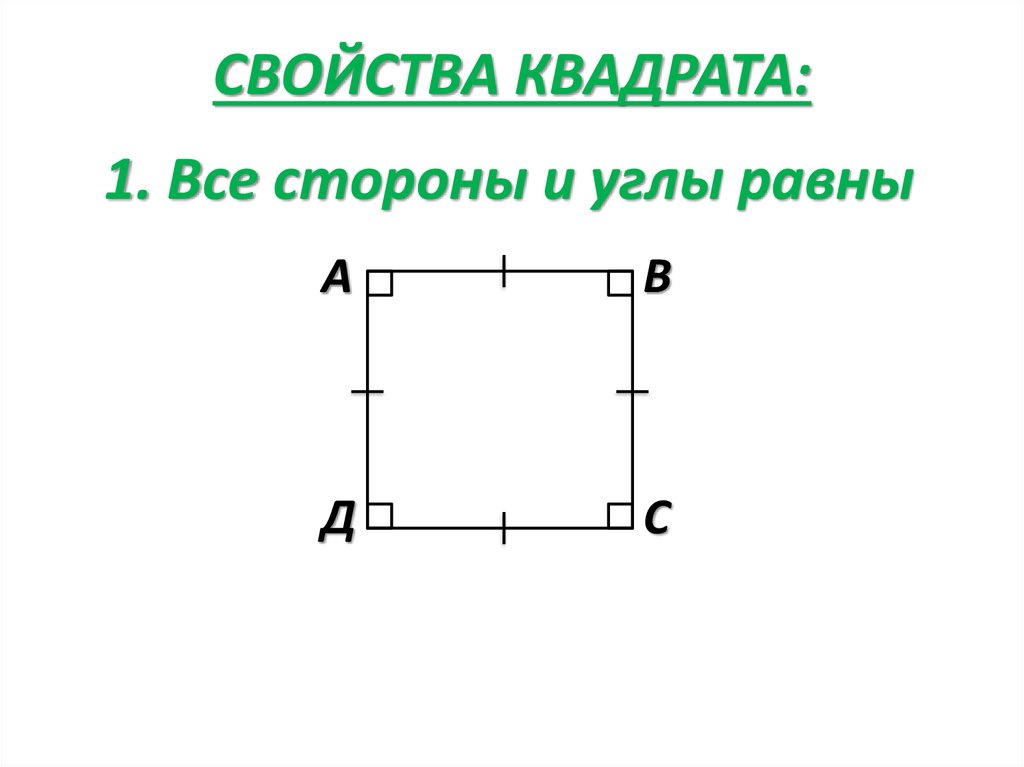
СВОЙСТВА КВАДРАТА:
1. Все стороны и углы равны
А
В
Д
С

15.

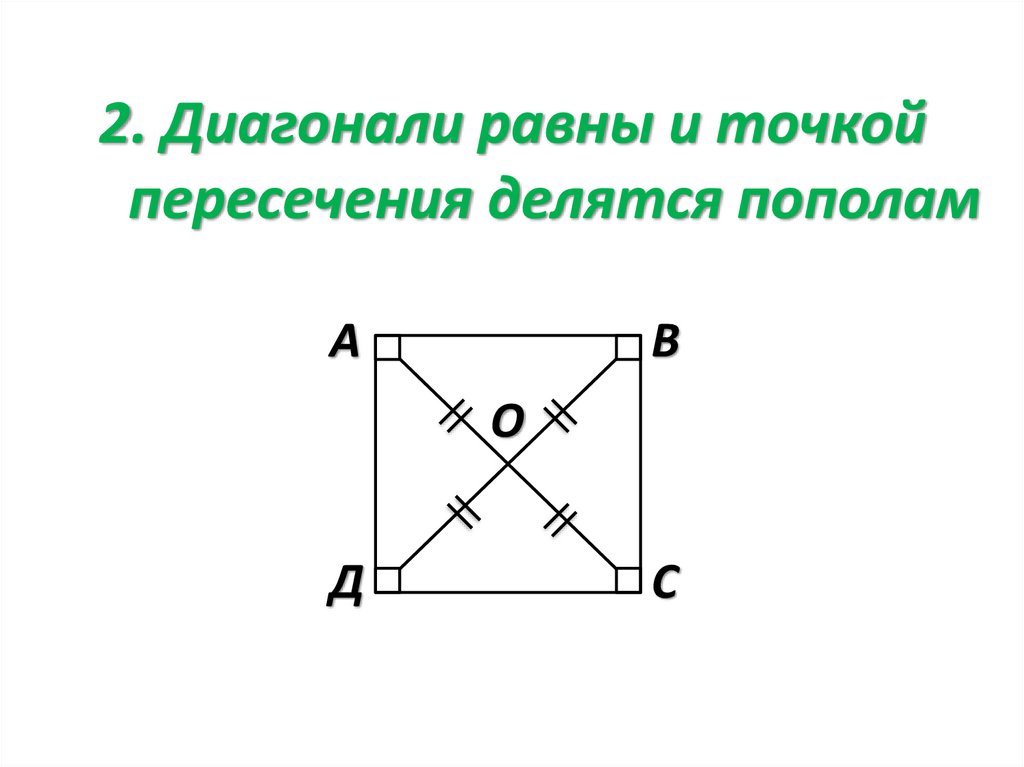
2. Диагонали равны и точкой
пересечения делятся пополам
А
В
О
Д
С

16.

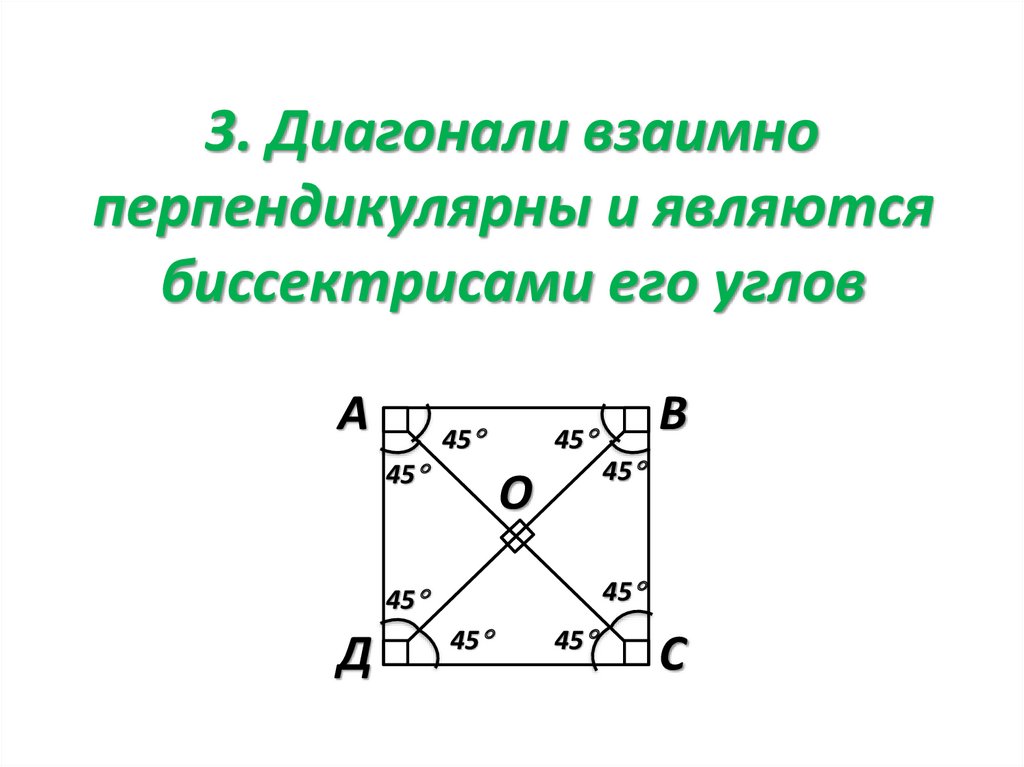
3. Диагонали взаимно
перпендикулярны и являются
биссектрисами его углов
А
45
45
45
О
45
45
45
Д
В
45
45
С

17.

ОСЕВАЯ И
ЦЕНТРАЛЬНАЯ
СИММЕТРИИ.

18.

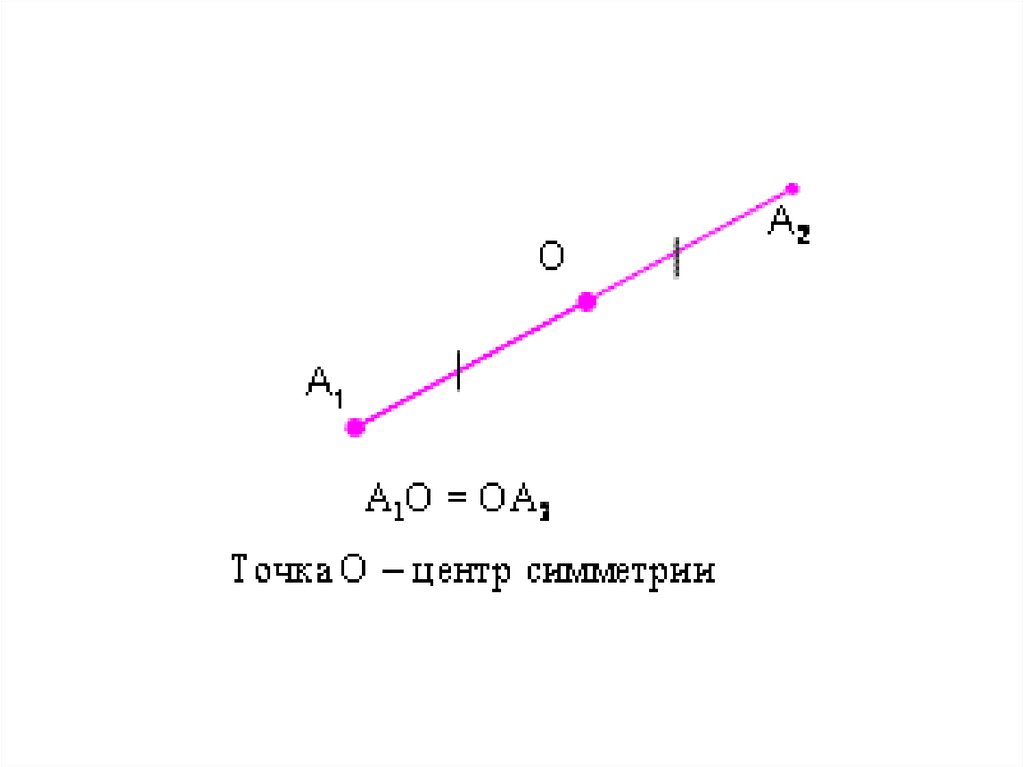
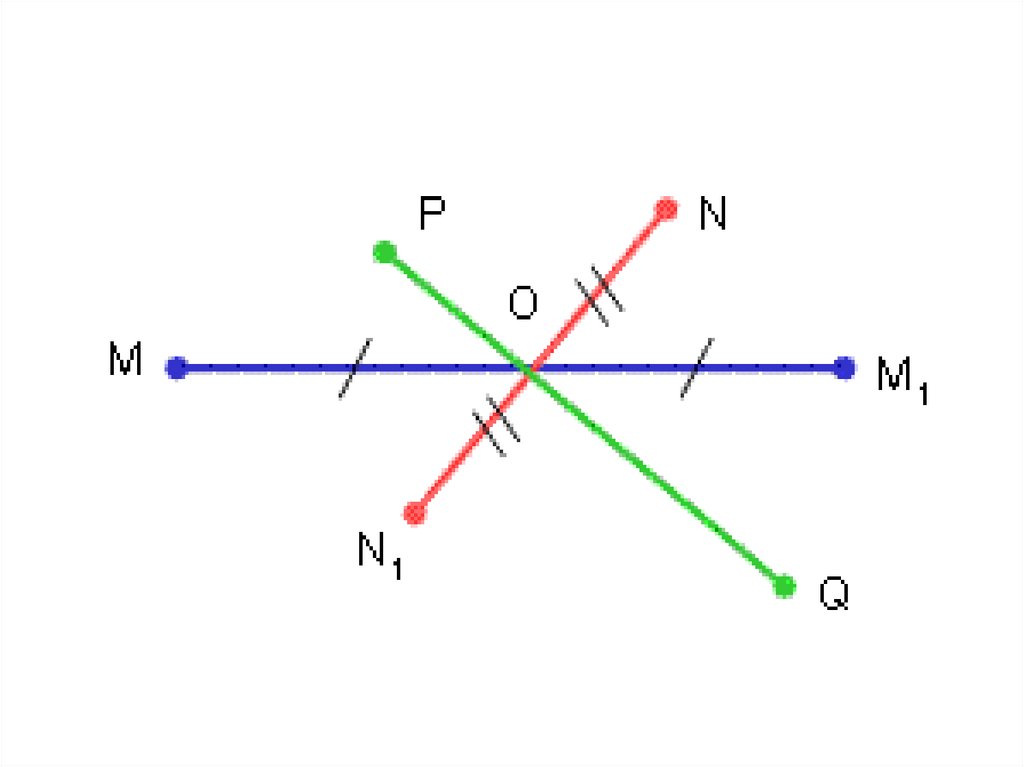
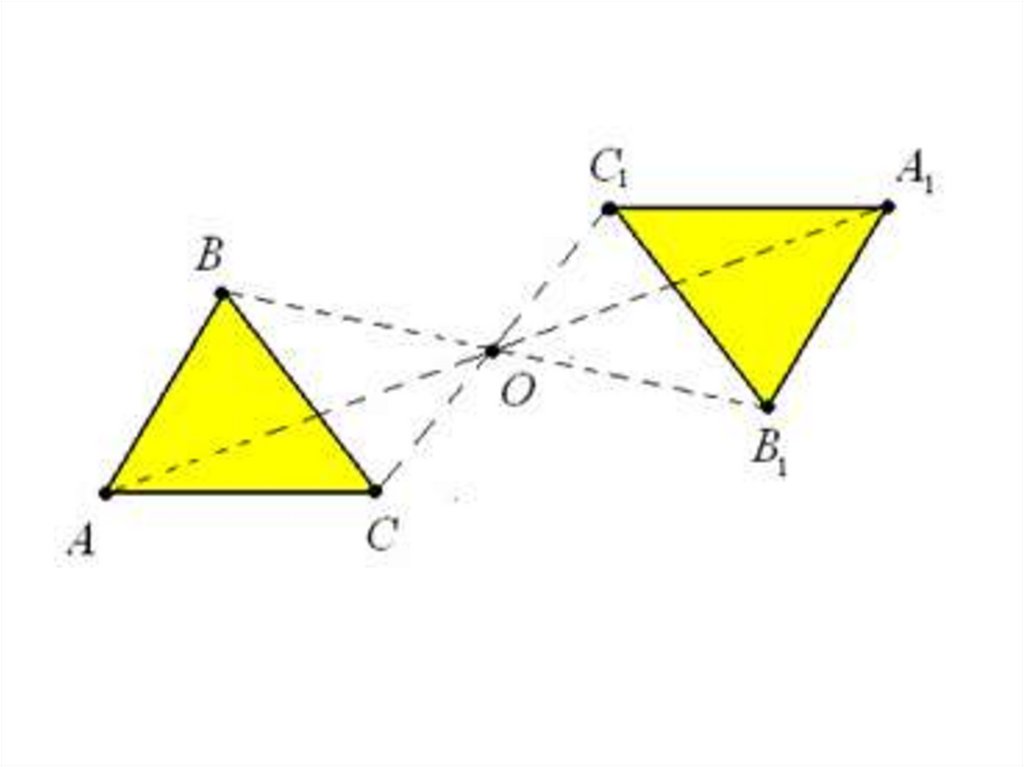
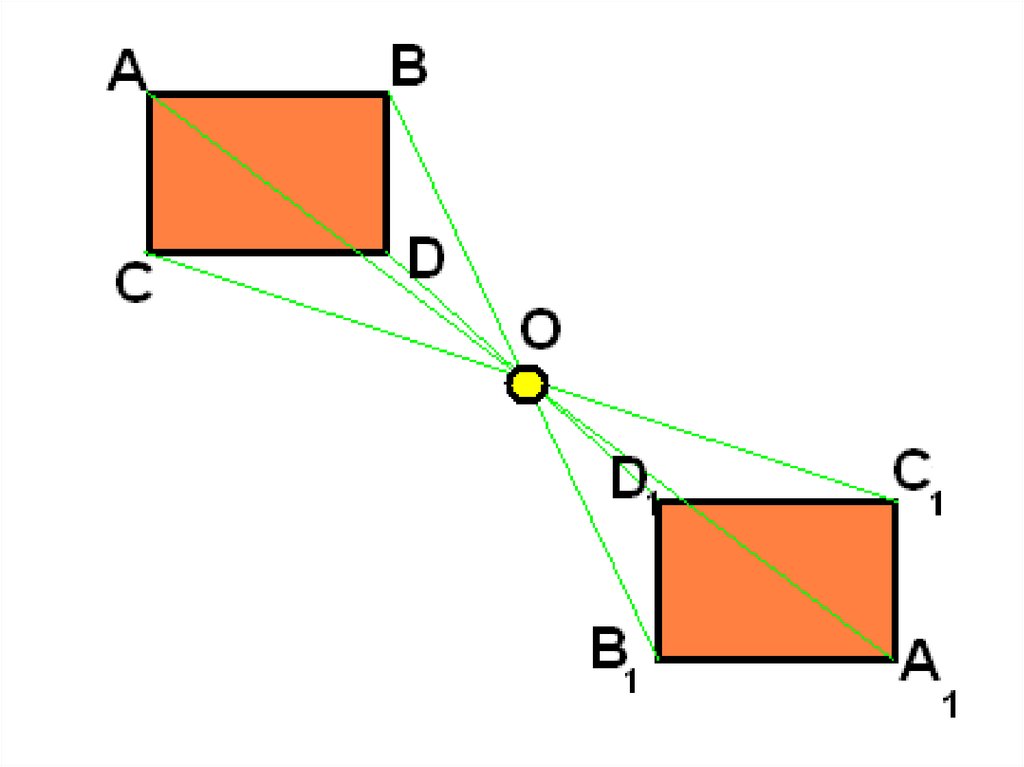
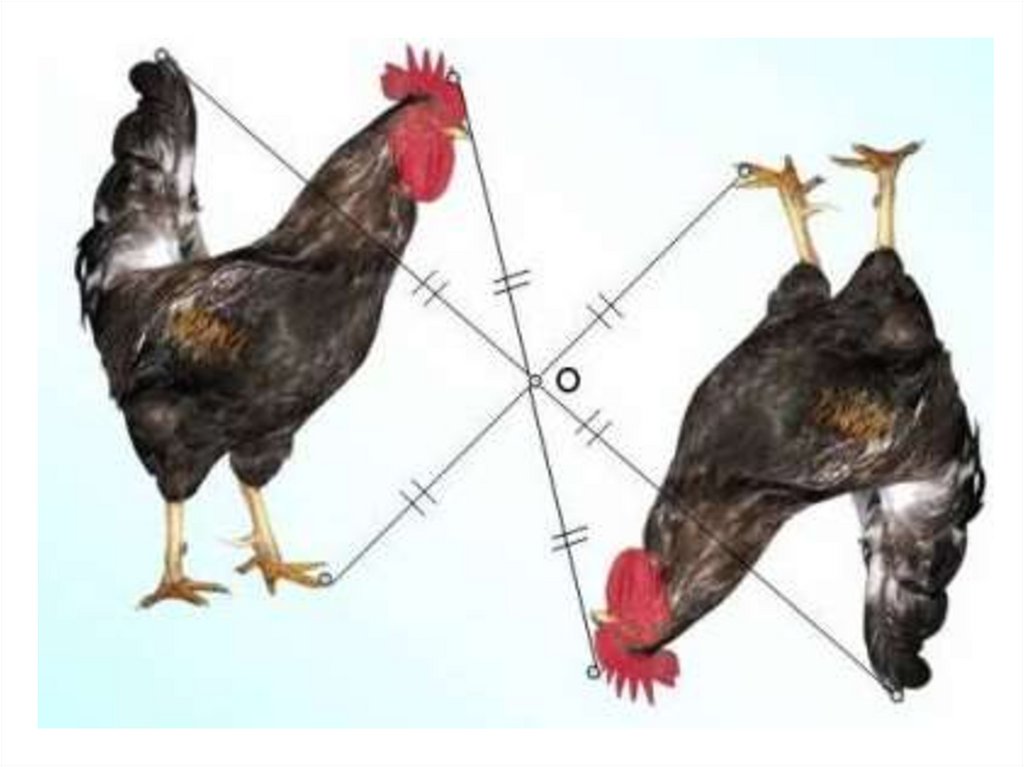
Центральная симметрия-это
симметрия относительно точки.

19.

20.

21.

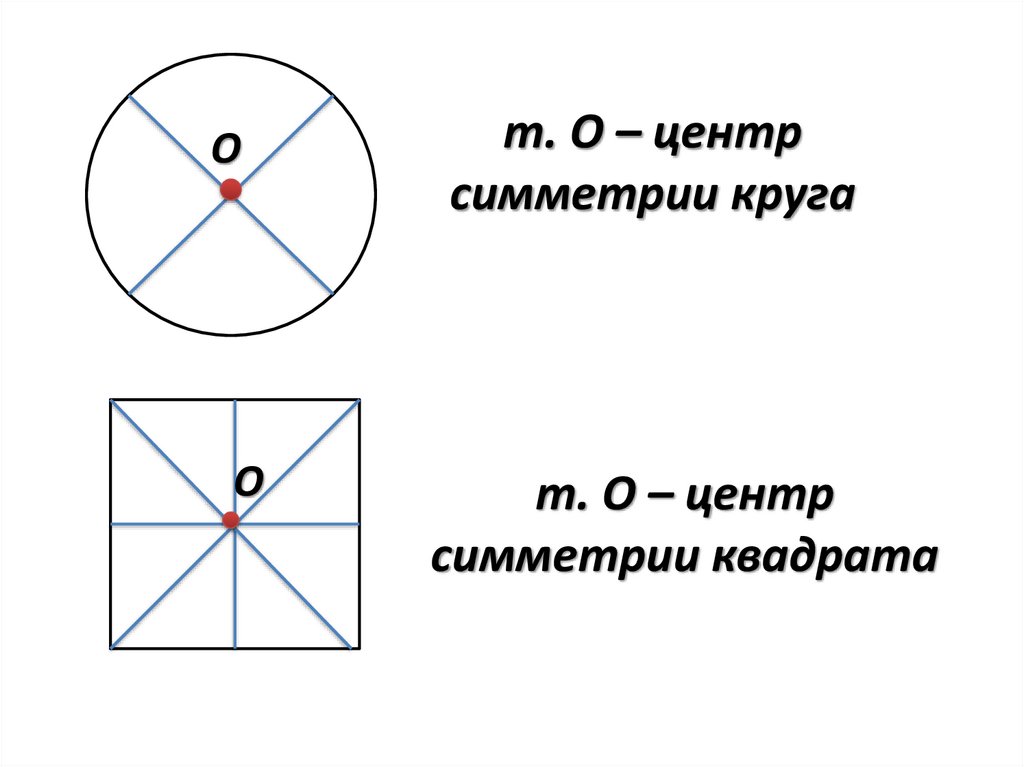
О
О
т. О – центр
симметрии круга
т. О – центр
симметрии квадрата

22.

23.

24.

25.

Осевая симметрия – это
симметрия относительно прямой.

26.

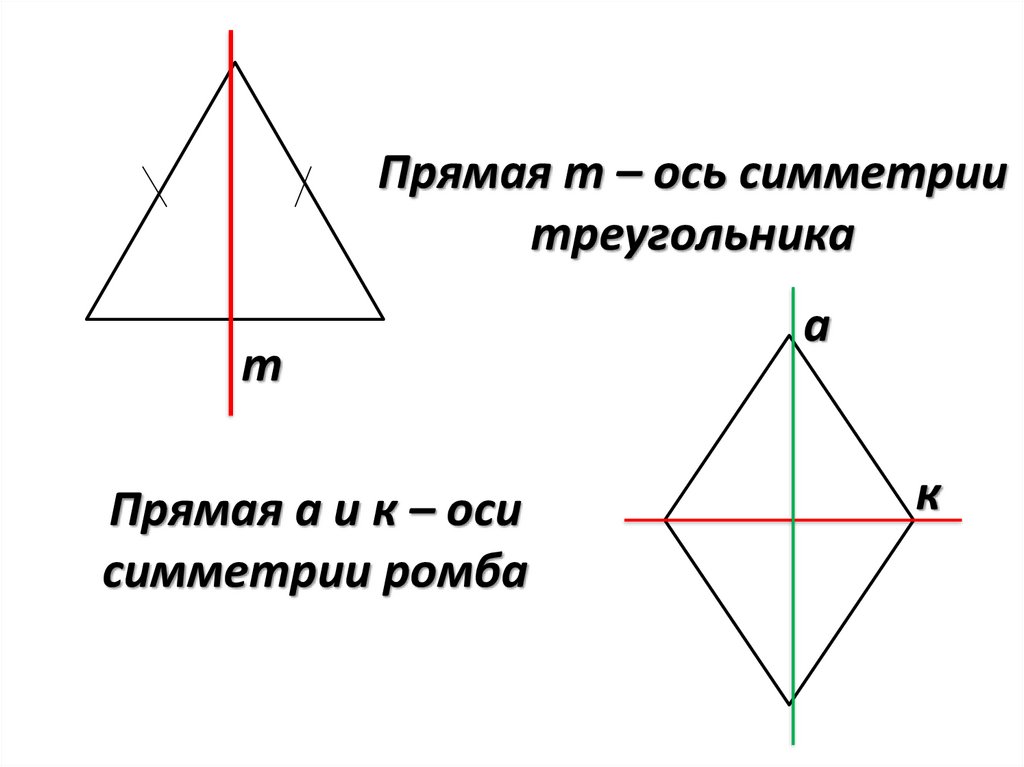
Прямая m – ось симметрии
треугольника
m
Прямая а и к – оси
симметрии ромба
а
к