Похожие презентации:
Объем пирамиды, конуса
1.
2.
34
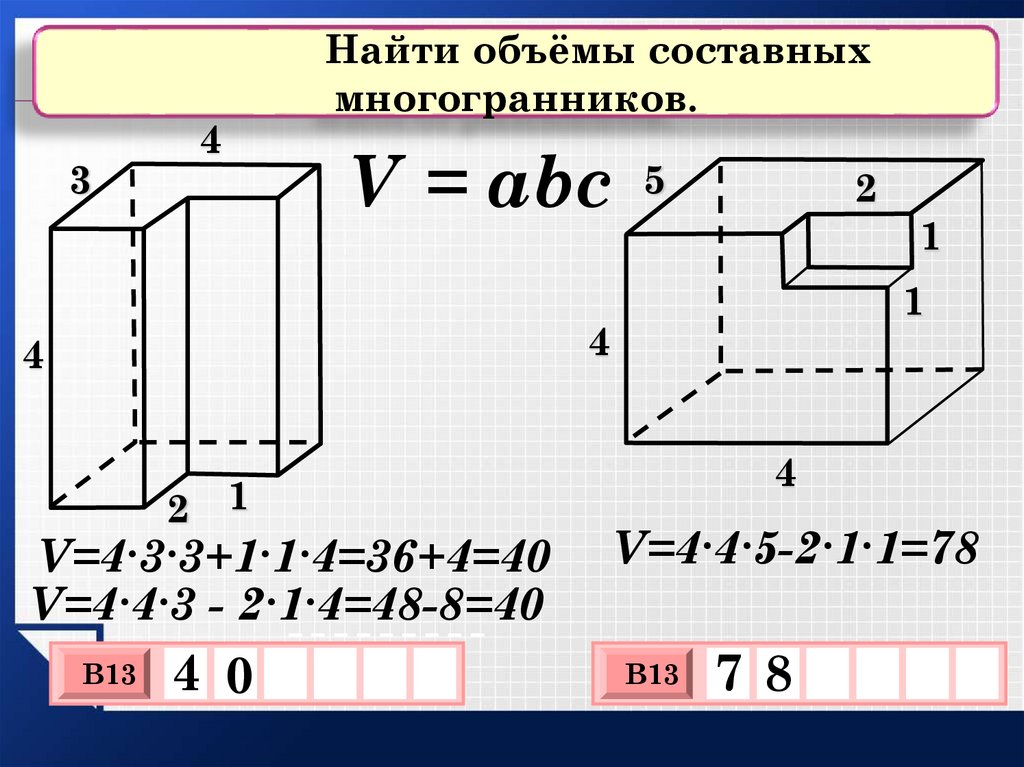
Найти объёмы составных
многогранников.
V = abc
5
2
1
1
4
4
4
2 1
V=4∙3∙3+1∙1∙4=36+4=40
V=4∙4∙3 - 2∙1∙4=48-8=40
В13
4 0
3
10 х
х
V=4∙4∙5-2∙1∙1=78
В13
7 8
3
10 х
х
3.
В основании прямой призмы лежитпрямоугольный треугольник с катетами 6 и 8.
5
Боковые ребра равны . Найдите объем
цилиндра, описанного π
около этой призмы.
8
Vц. = Sосн h
6
5
π
5
2
Vц. = π r h
Vц.
5
5
= π5
= π 25
π
π
2
В 13
1 2 5
3
10 х
х
4.
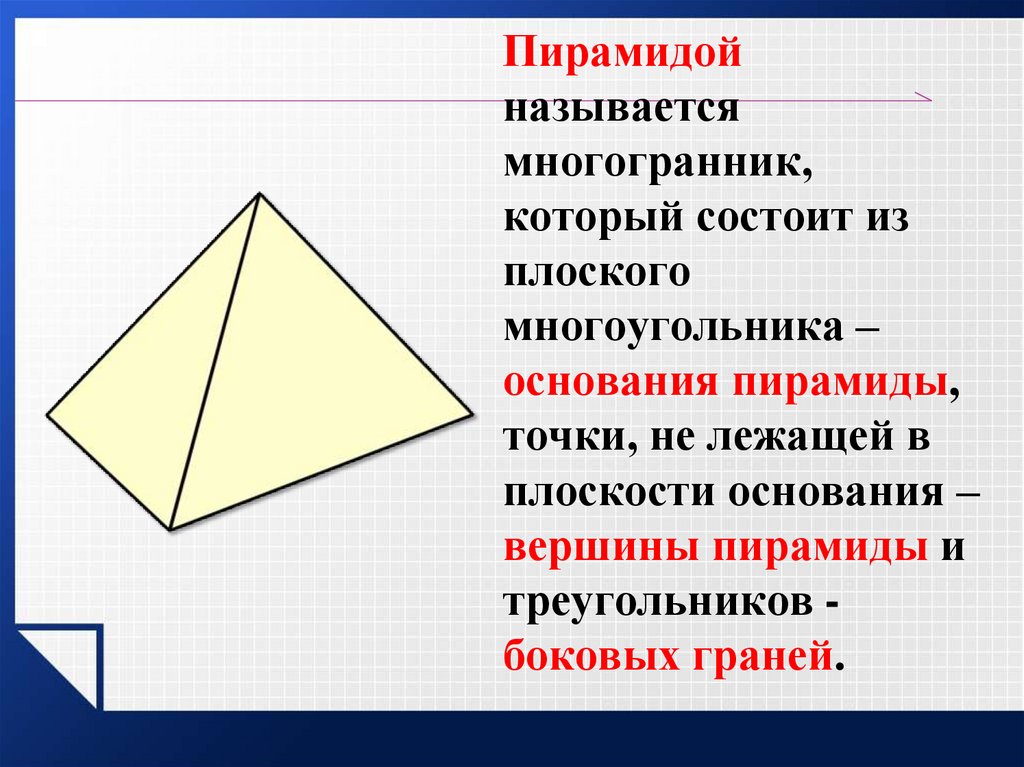
Пирамидойназывается
многогранник,
который состоит из
плоского
многоугольника –
основания пирамиды,
точки, не лежащей в
плоскости основания –
вершины пирамиды и
треугольников боковых граней.
5.
Термин “пирамида” заимствованиз греческого “пирамис” или “пирамидос”. Греки в
свою очередь позаимствовали это слово, как
полагают, из египетского языка. В папирусе Ахмеса
встречается слово “пирамус” в смысле ребра
правильной пирамиды. Другие считают, что термин
берет свое начало от форм хлебцев в Древней
Греции “пирос” - рожь). В связи с тем, что форма
пламени иногда напоминает образ пирамиды,
некоторые средневековые ученые считали, что
термин происходит от греческого слова “пир” огонь. Вот почему в некоторых учебниках геометрии
XVI в. пирамида названа “огнеформное тело”.
6.
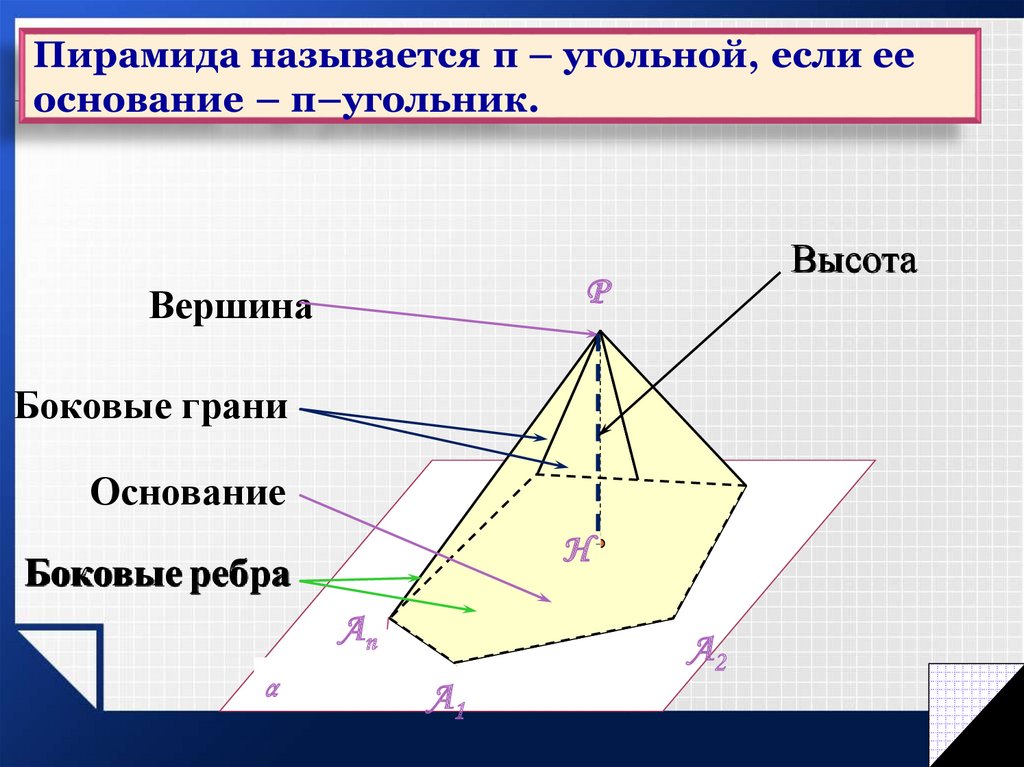
ВысотаP
Вершина
Боковые грани
Основание
H
Боковые ребра
Аn
α
А2
А1
7.
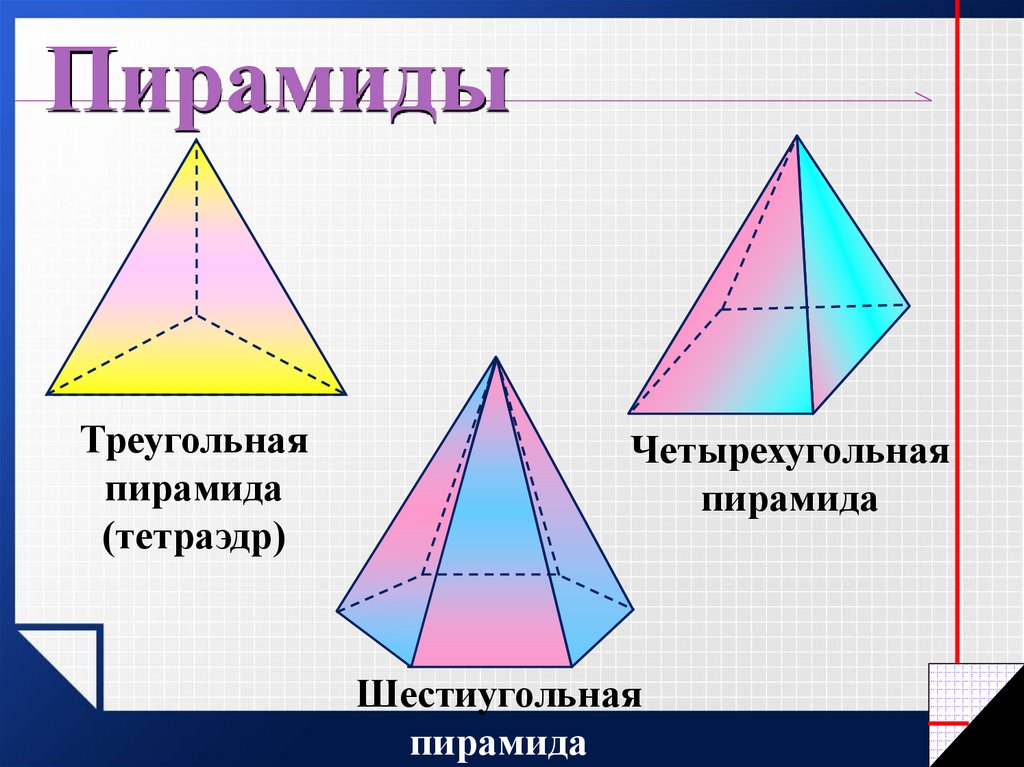
ПирамидыТреугольная
пирамида
(тетраэдр)
Четырехугольная
пирамида
Шестиугольная
пирамида
8.
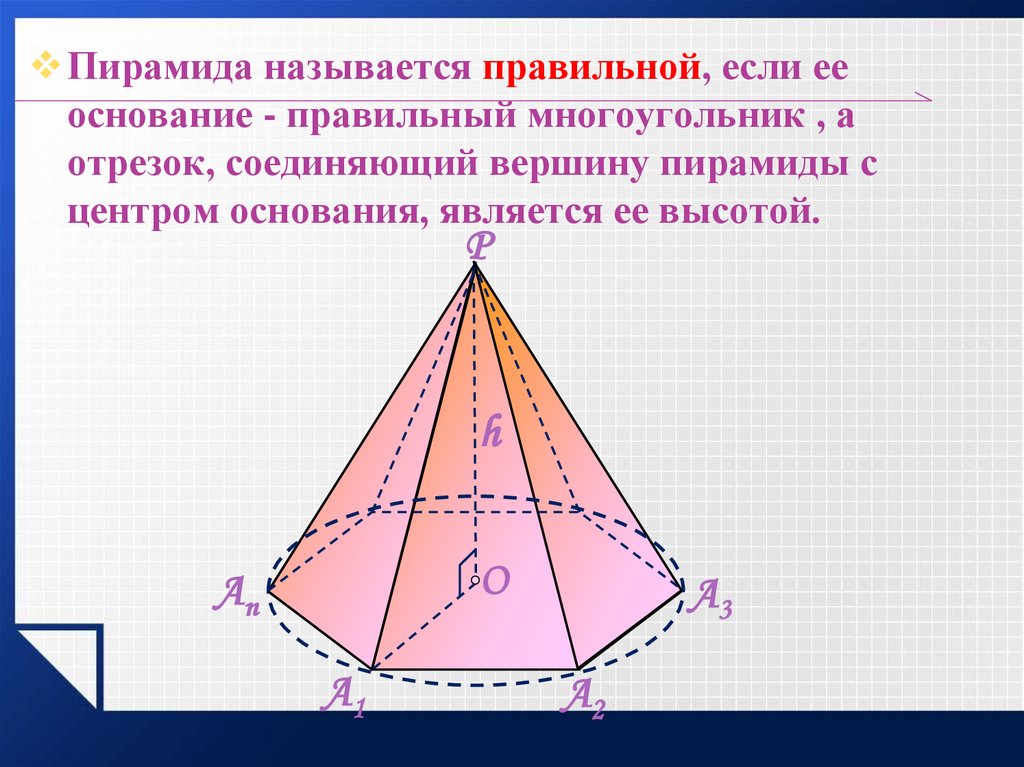
Пирамида называется правильной, если ееоснование - правильный многоугольник , а
отрезок, соединяющий вершину пирамиды с
центром основания, является ее высотой.
P
h
O
Аn
А1
А3
А2
9.
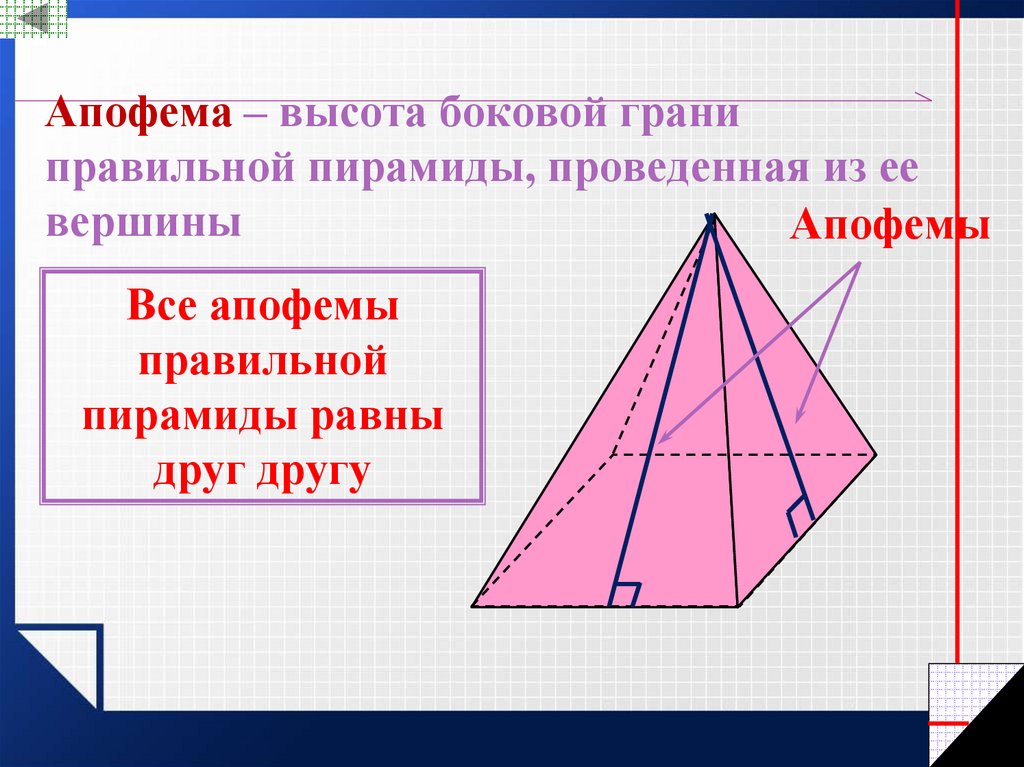
Апофема – высота боковой граниправильной пирамиды, проведенная из ее
вершины
Апофемы
Все апофемы
правильной
пирамиды равны
друг другу
10.
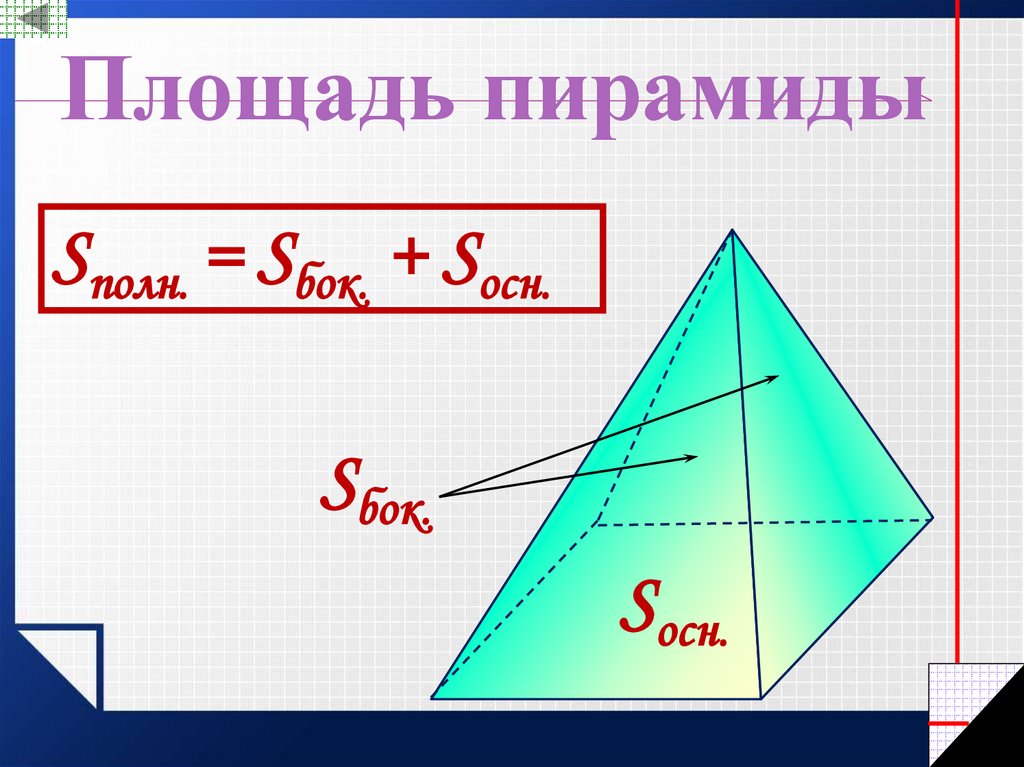
Площадь пирамидыSполн. = Sбок. + Sосн.
Sбок.
Sосн.
11.
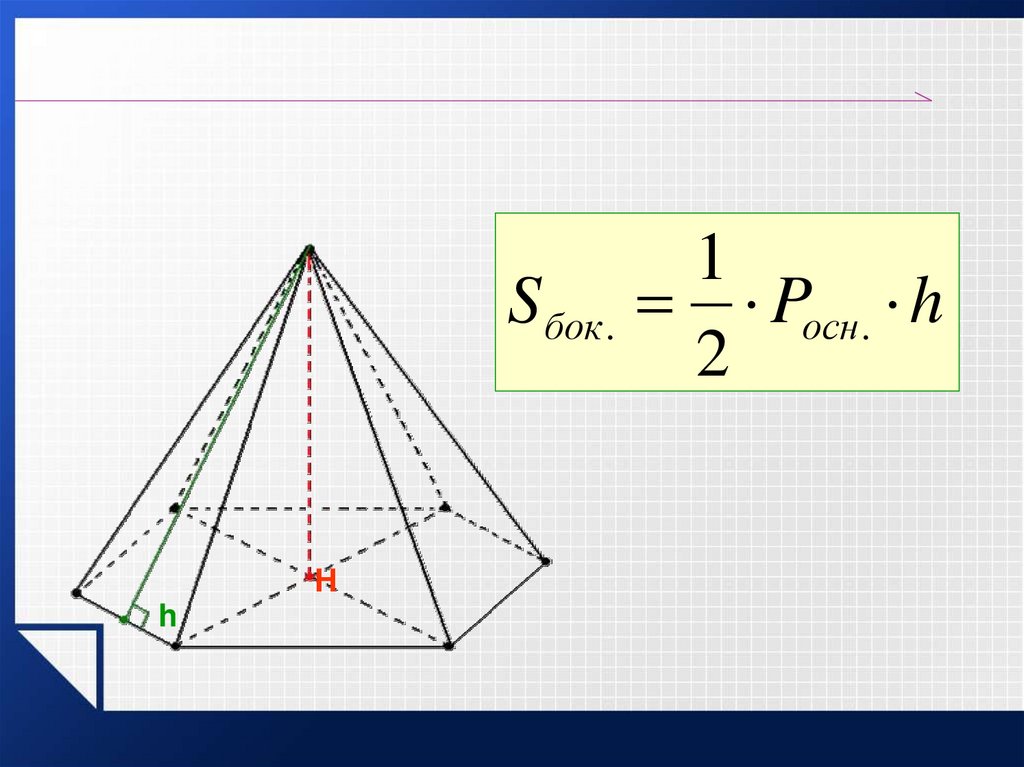
S бок .H
h
1
Pосн. h
2
12.
Свойства пирамиды:У правильной пирамиды:
боковые ребра равны;
боковые грани являются
равными равнобедренными
треугольниками;
апофемы равны;
площадь боковой
поверхности правильной
пирамиды равна половине
произведения периметра на
апофему.
13.
1∙h
V = Sосн.
3
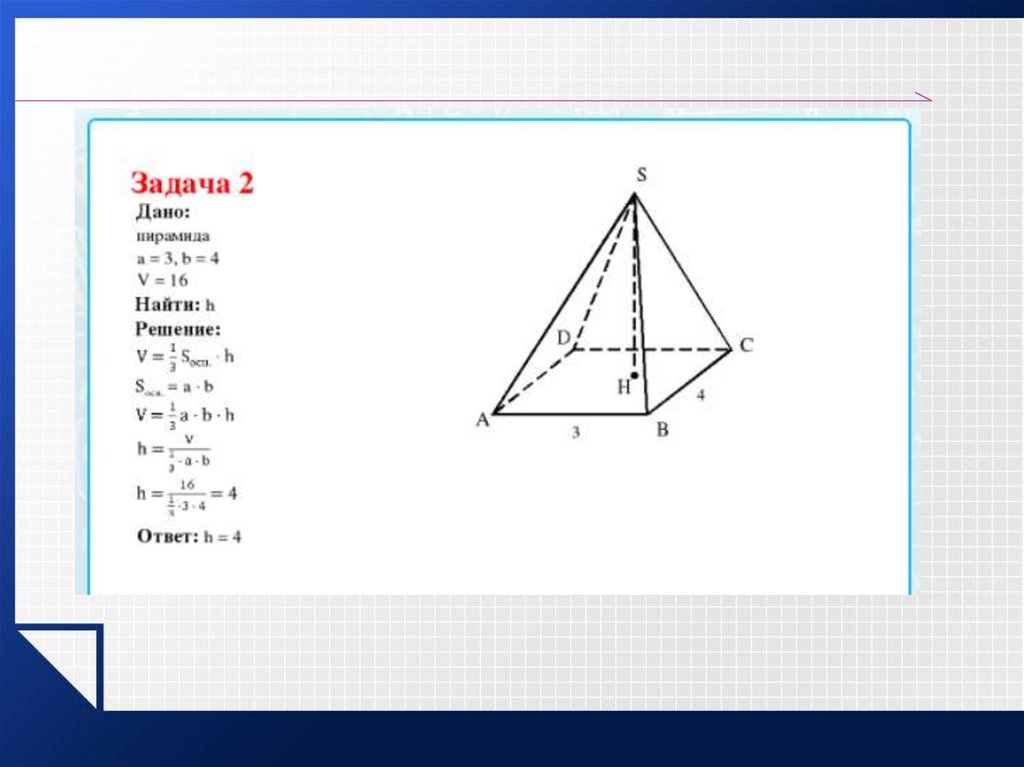
14.
15.
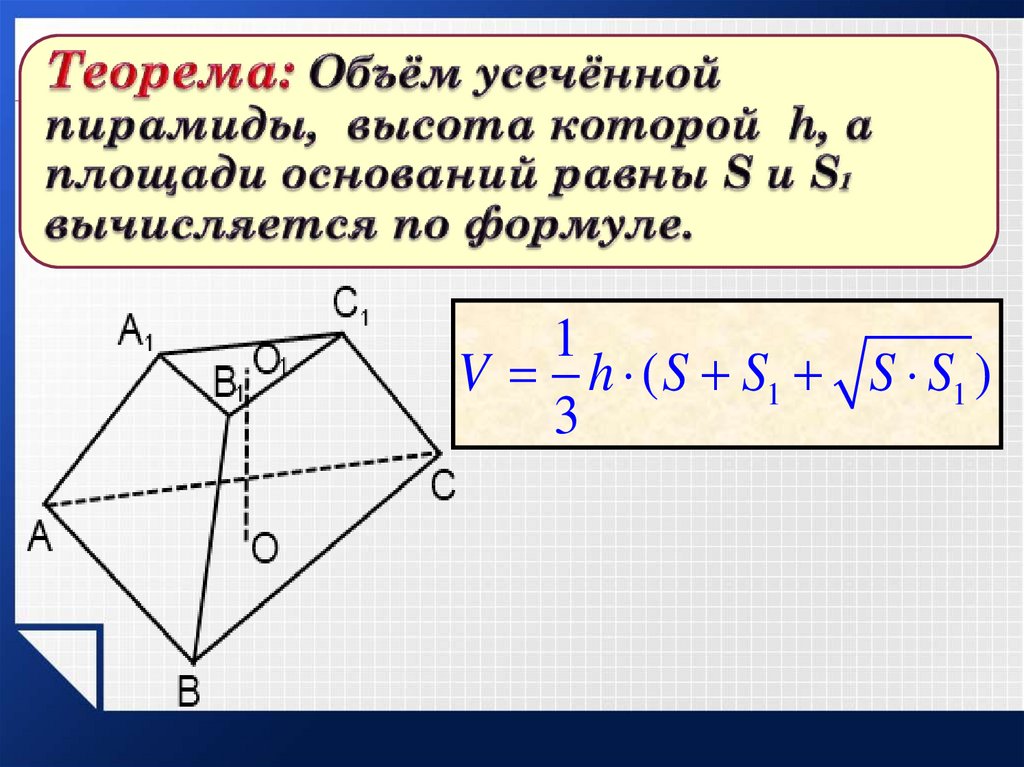
16.
1V h ( S S1 S S1 )
3
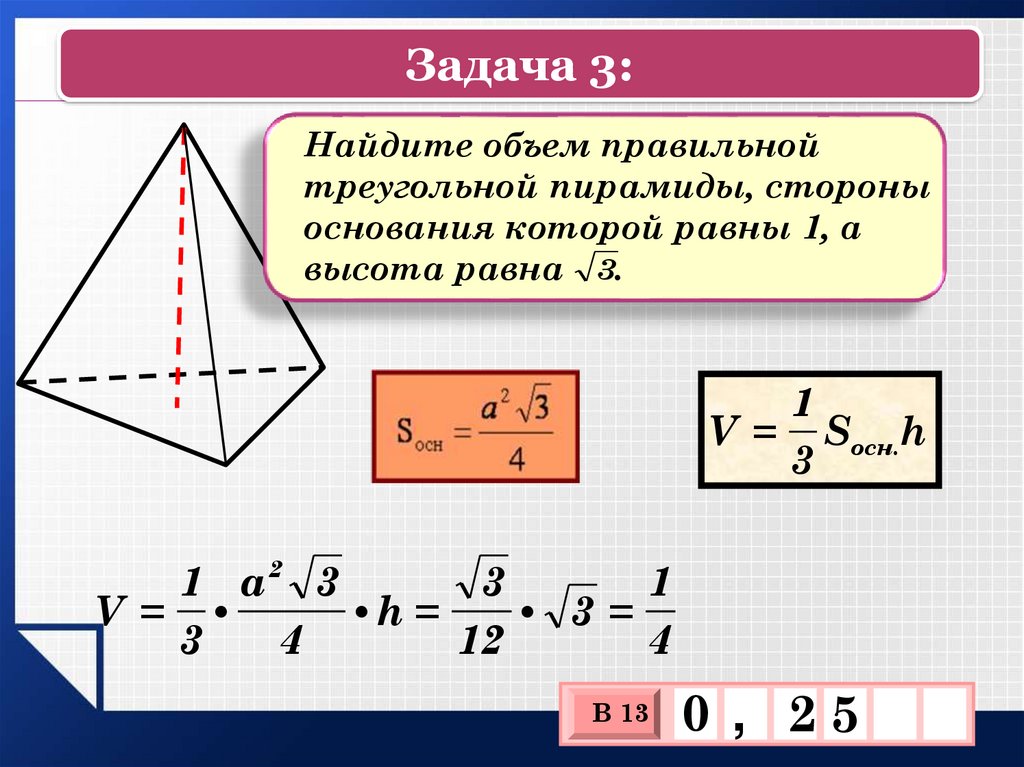
17.
Задача 3:Найдите объем правильной
треугольной пирамиды, стороны
основания которой равны 1, а
высота равна 3.
1
V = Sосн.h
3
1 a2 3
3
1
V =
•h =
• 3=
3
4
12
4
В 13
0 , 25
3
10 х
х
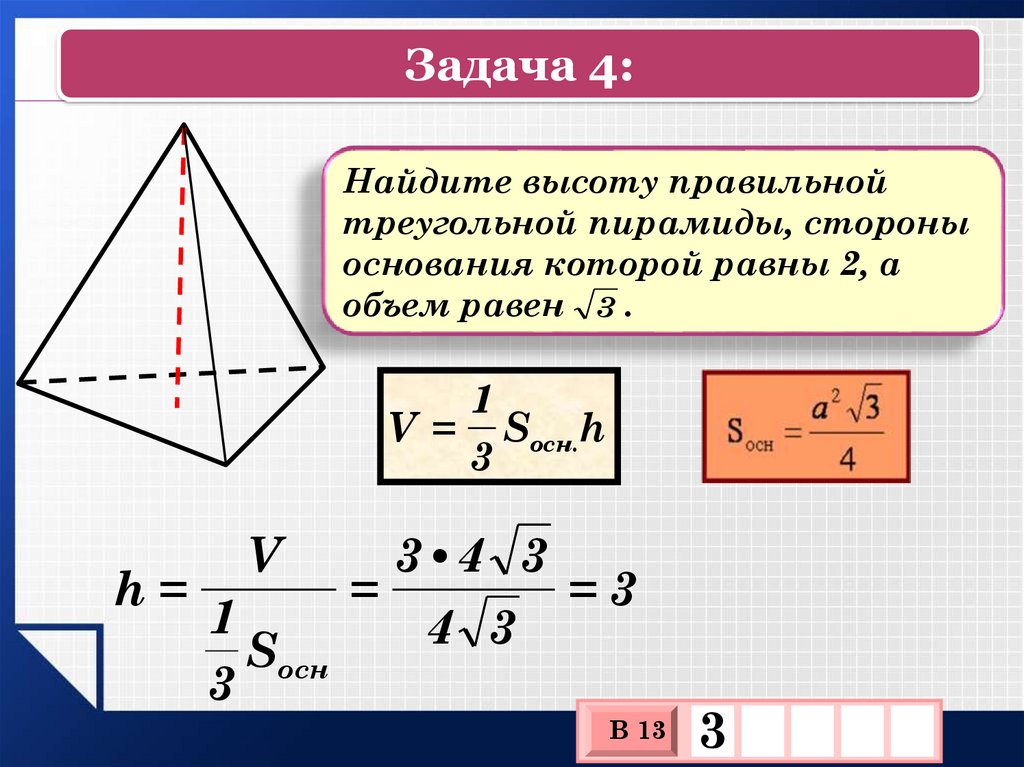
18.
Задача 4:Найдите высоту правильной
треугольной пирамиды, стороны
основания которой равны 2, а
объем равен 3 .
1
V = Sосн.h
3
h=
V
1
Sосн
3
3 •4 3
=
=3
4 3
В 13
3
3
10 х
х
19.
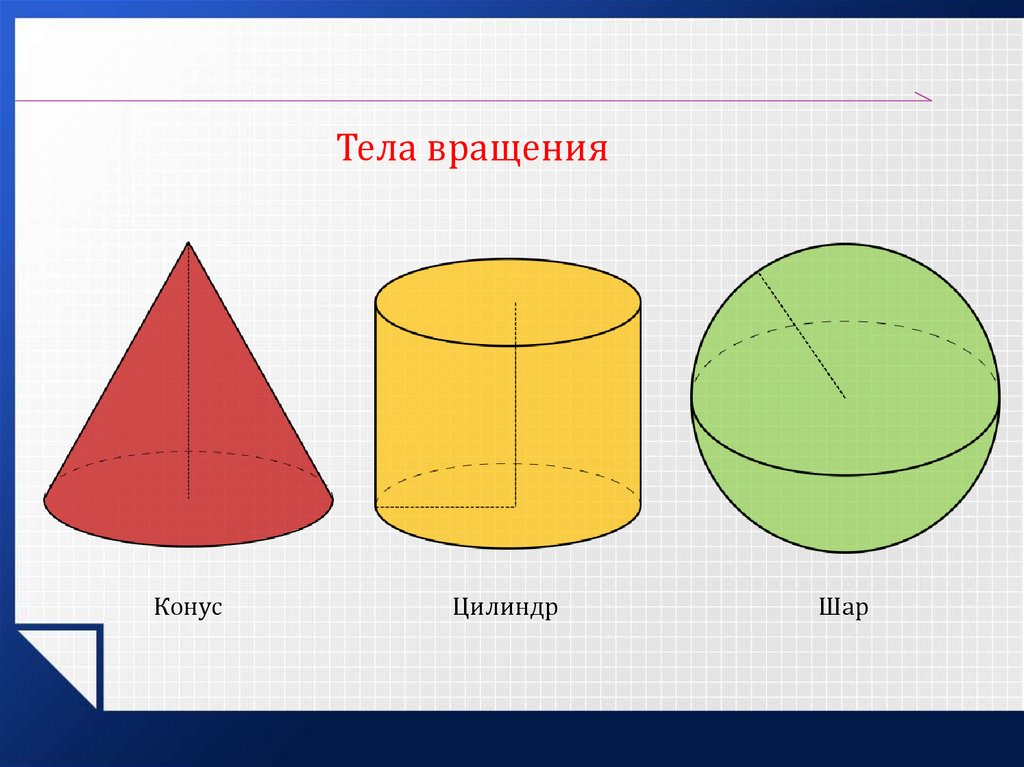
Тела вращенияКонус
Цилиндр
Шар
20.
ОпределениеКонусом называется тело,
которое состоит из круга —
основания конуса, точки,
не лежащей в плоскости
этого круга, вершины конуса
и всех отрезков,
соединяющих вершину
конуса с точками основания
21.
ТеоремаОбъём конуса равен одной трети
произведения площади основания на высоту
22.
Формула объёма усечённого конусаV — объём усеченного конуса
h — высота
S и S1 — площади оснований
O1
R1
h
R
O
23.
Задача 5Дано:
Δ прямоугольный
r = 4, h = 3
4
Найти:
4
V конуса
Решение:
1) R — радиус основ. конуса
h — высота конуса
Sосн. = πR2
V = πR2h
Ответ: V = 16π
R
3
h
24.
Задача 6Дано:
Δ прямоугольный
h = 4, r = 3
Найти:
V конуса
Решение:
R = b = 3, h = a = 4
Sосн. = πR2
Ответ: V = 12π
4 h
3
R
3
25.
Задача 7Дано:
B
конус
R = 6 см
∠ВСО = 45°
Найти: V
Решение:
R
O
h = BO, ΔBOC — прямоуг.
⇒ ΔBOC — равноб.
BO = OC = 6 см
Ответ: V = 72π
C












 Математика
Математика








