Похожие презентации:
Теоретические основы электротехники. Теория электромагнитного поля
1.
Теоретические основы электротехникиТеория электромагнитного поля
ВШВЭ, проф. Л. И. Сахно 2020
1
2.
Применение функций комплексного переменногодля описания плоскопараллельных полей
3.
Функция потокаЛинии равного потенциала в плоскости xOy определяются уравнением:
U ( x, y) const
U const
E
- поток вектора E сквозь поверхность, которую описал бы
отрезок MmA, перемещаясь параллельно самому себе в
направлении оси Oz и проходя путь l
V E / l
- поток на единицу длины проводов
V x, y const - если все точки M (x,y) лежат на одной и той
же линии напряженности поля
V x, y
- многозначная функция потока
Линии равной функции потока совпадают с линиями напряженности
Одна из линий напряженности выбирается в качестве линии нулевого
потока. Выбор может быть сделан произвольно
4.
Выражение для напряженности через функцию потокаУсловимся считать функцию потока, возрастающей влево от вектора для
наблюдателя, расположившегося так, чтобы для него вектор направлен снизу
вверх
U
V
E
n
a
Для декартовой системы координат:
U
V
x
y
U
V
Ey
y
x
Ex
5.
Уравнения Лапласа для функций потенциала и потокаU
V
x
y
U
V
Ey
y
x
Ex
(1)
Продифференцируем первое уравнение по x , а второе по y
2U 2V
2
x
x y
2U 2U
2 0
2
x
y
2U
2V
2
y
x y
Продифференцируем первое уравнение по y , а второе по x :
U V
2
x y y
2
2
U
V
2
x y
x
2
2
2V 2V
2 0
2
x
y
Таким образом функции U и V удовлетворяют уравнению Лапласа
6.
Функция комплексного переменногоПлоскость комплексного переменного
z = x+jy = r·e j
Рассмотрим комплексную величину:
j
x, y
x, y - функции
x
и
y
x, y - регулярная аналитическая функция комплексного переменного
Функция однозначна, непрерывна и имеет непрерывную производную во всех
точках области
Условия Коши-Римана для функции комплексного переменного:
y x
x
y
При этих условиях производная функции
не зависит от направления дифференцирования
7.
Сравнение условий Коши-Римана и выражений для напряженности поля:x
y
U
V
Ex
x
y
U
V
Ey
y
x
y x
j V jU f ( z ) - комплексный потенциал поля
Составляющие напряженности поля :
U
EX
x
x
U
Ey
y
y
8.
E E Ex
y
2
2
x
2
2
y
(1)
y x
(2)
Подставляя (2) в (1) , получаем:
d
E
dz
x x
2
2
Задача расчета поля решена, если найдена аналитическая функция f ( z) ,
удовлетворяющая граничным условиям на поверхности провода
Исследуя различные аналитические функции комплексного переменного
можно найти соответствующие им поля и получить таким образом решения
для ряда конкретных случаев
9.
Метод заданного комплексного потенциала.Этот метод расчета плоскопараллельных полей заключается в предварительном
задании некоторой комплексной функции на плоскости – комплексного потенциала
W(z) и последующего определения, какой геометрической области предложенная
функция W(z) соответствует. Координаты точки на плоскости могут быть заданы в
декартовой или полярной системе: z
= x+jy = r·e j
. Пусть комплексный потенциал задан в виде:
W(z) = az + b = (ax + b) + jay = V + jU ,
тогда:
V = ax + b = const - уравнение линии напряженности, т.е. x = const
вертикальные линии, а
U = ay = const - уравнение линии равного потенциала т.е. y = const
горизонтальные линии.
10.
При а > 0 с ростом x и y растут соответственно V и U . Принимая постояннымприращения потенциала и функции потока ( V = const и U = const), получаем
постоянство приращения координат при переходе от линии к линии ( x = const и
y = const )
V1
y
V2
V3
V4
V5
U1
U2
U3
U4
U5
x
Совместив поверхности двух
проводников с двумя линиями
равного потенциала (U1 и U4),
получаем картину поля между
двумя плоскими проводящими
пластинами (внутри плоского
конденсатора). Таким образом, мы
установили, какой геометрической
области соответствует принятый
комплексный потенциал.
11.
. Пусть комплексный потенциал задан в виде:W(z) = jA ln z = jA ln(r·ej ) = jA ( ln r + j ) = – A + jA ln r = V + jU,
тогда:
V = – A = const уравнение линии напряженности, т.е. = const. Эти линии
представляют собой лучи, исходящие из начала координат;
U = A ln r = const уравнение линии равного потенциала, т.е. r = const . Эти
линии представляют собой концентрические окружности с центром в начале
координат.
Принимая постоянным приращения потенциала и функции потока ( V = const и
U = const), получаем постоянство приращения координаты = const при
переходе от одной к другой линии напряженности и постоянство отношений
rk 1
const
радиусов соседних линий равного потенциала
rk
12.
Поле уединенного заряженного кругового цилиндраПри =2 получаем поверхность, охватывающую весь проводник с полным зарядом
V3
V4
U3
V2
U2
U1
U1 U2 U3
V1 V2 V3
V1
q
E
q
V
l
V A 2
A
2
V
2
U
ln r
2
13.
Поле создается тонкой заряженной нитью, расположеннойв точке с координатой z = z0
W = j A ln( z – z0)
W(z) = jA ln z
jy
E
z
0
z – z0
z0
x
14.
. Поле двух тонких заряженных нитейДля двух заряженных нитей с зарядами 1 и 2, расположенных в точках с координатами z10 и
запишем выражение для комплексного потенциала, воспользовавшись принципом наложения:
z20
W (z) = jA1 ln (z–z10) + jA2 ln (z–z20) + C1 + j C2.
C1 и C2 – произвольные постоянные, зависящие от выбора места расположения начальных (нулевых)
линий функции потока и потенциал
1
A1
2
2
A2
2
1 = – 2 =
Комплексный потенциал в произвольной точке имеет вид:
z z10
W j
ln
C1 jC2
2 z z 20
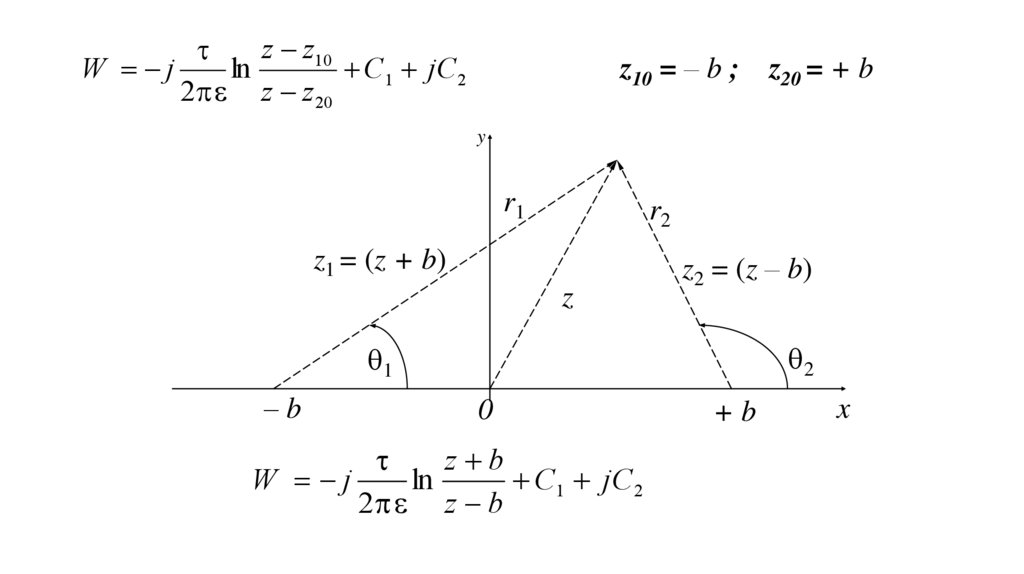
15.
z z10W j
ln
C1 jC2
2 z z 20
z10 = – b ;
z20 = + b
y
r1
r2
z1 = (z + b)
z
z2 = (z – b)
2
1
–b
0
z b
W j
ln
C1 jC 2
2 z b
+b
x
16.
z1 = z + b = r1 ej 1
z b
W j
ln
C1 jC 2
2 z b
z2 = z – b = r2 e
j 2
r1 j ( 1 2 )
W j
ln e
C1 jC2
2 r2
r2
W j
ln jC2
( 1 2 ) C1 = V + j U
2 r1
2
Положим C2=0 , тогда получим U=0 при r1=r2, то есть линия нулевого потенциала – это
ось ординат
r2
U
ln C 2
2 r1
r2
U
ln C 2 const
2 r1
V
( 2 1 ) C 1
2
r2
const
r1
17.
Линии равного потенциала в системе двух заряженных проводовЛинии равного потенциала – это окружности с центрами на оси OX с координатами центра:
r2
k const
r1
и радиусом:
1 k2
x0
b
2
1 k
y0 0
2k
R
b
2
1 k
Чтобы приращение потенциала при переходе от любой линии равного потенциала к соседней
оставалась постоянным, должно быть соблюдено условие:
r2,
r2, 1
U U 1 U
ln
ln
2 r1, 1
r1,
k 1
ln
const
k
2
k 1
B const
k
18.
Линии равной напряженности поля в системе двух заряженных проводовПоложив в выражении для функции потока C1=0, получим V=0 при 2 1
2 1 const
V
( 2 1 ) const
2
Линия напряженности поля является уравнением дуги окружности, пересекающейся
с проводами
Координаты центров окружностей:
V
V
1 V
x0 0
y0 bctg
y0 bctg ( ) bctg
V V 1 V
const
19.
Картина поля двух линейных проводов и реальнойлинии передачи
Формулы для определения положения линейных
проводов (электрических осей) , эквивалентным двум
проводам круглого сечения
h x0
- координата центра окружности равного потенциала
1 k2
h
b
2
1 k
B 3
2k
R
b
2
1 k
b h2 R 2
/ 6
На рисунке заштрихованы сечения проводов около контуров сечений
20.
Поле параллельных несоосных цилиндровПоложение плоскости нулевого потенциала:
D R R
h1
2D
2
2
1
2
2
h2
D R R
2D
2
2
1
2
2
h1
b h12 R12 h22 R22
D R R
2D
2
2
1
2
2
D 2 R22 R12
h2
2D
- положение электрических осей



















 Физика
Физика








