Теоретические основы электротехники. Теория электромагнитного поля. Лекция 4

1.

Теоретические основы электротехники
Теория электромагнитного поля
ВШВЭ, проф. Л. И. Сахно 2021
1

2.

Метод зеркальных изображений

3.

Используется для расчета поля заряженных проводников , расположенных вблизи
плоских поверхностей, ограничивающих проводящую среду
jy
+q
+q
jy
h
h
x
x
U = const
Сопоставляя левую и правую картины полей , можем
утверждать, что из-за одинаковой геометрии и граничных
условий картины поля в верхней полуплоскости идентичны,
а, следовательно, все характеристики поля полностью
совпадают.
U = const
h
–q

4.

Применение метода зеркальных изображений возможно и в случае, когда заряды находятся внутри
диэлектрика между гранями двугранного угла « », образованного проводящими поверхностями, если
- 2
+ 1
+ 21
- 11
Отразим заряд + 1 от вертикальной стенки, вследствие чего появится второй заряд противоположного
знака – 2 , и оба эти заряда оказались расположенными над горизонтальной проводящей плоскостью.
Отразим эти заряды в горизонтальной плоскости и получим еще два заряда ( 21 и – 11). Полная система из
четырех зарядов образует картину поля в диэлектрике, часть которой в первом квадранте совпадает с
исходной картиной поля.

5.

Метод конформных отображений

6.

Расчет поля методом конформных отображений основан на том, что существует
возможность отобразить с помощью некоторого математического
преобразования заданную область в комплексной плоскости « z » (x + jy) на так
называемую каноническую область в комплексной плоскости « ω » ( ξ+j ).
jy
Z
1
Z
2
ZK
X
j
ω
1
2
ω
ωk
ξ
Преобразование называется конформным, так как при переходе от одной области к другой либо обратно сохраняются
углы в точках пересечения между любыми линиями в обеих областях z = ω

7.

Существует общий подход к преобразованию произвольной многоугольной
области, ограниченной ломаной линией на верхнюю полуплоскость и обратно с
помощью интеграла Кристоффеля-Шварца
1. Двугранный угол ( ) – поле между двумя проводящими плоскостями,
сходящимися под углом
jy
j
z
B
U=0
C
C
A
U=0
B
X
( z)
A
ξ

8.

Положение точки на первой грани (точка A) :
z A rA e
j0
- в исходной области Z
A rA
- в области ω
Положение точки на второй грани (точка B) :
z B rB e
j
- в исходной области Z
B rB e j rB
- в области ω
Положение любой точки на биссектрисе угла (точка C):
z С rС e
j
2
- в исходной области Z
С rС e
j
2
jrС
- в области ω

9.

2. Бесконечно глубокий проводящий паз шириной d
jy
F
A
j
Z
D
E
F
E
d
B
O
C
X
z
sin
d
A
B
O
C
D

10.

z C ,B
d
2
Положение угловых точек B и C
d
2
C ,B sin
sin 1
d
2
Положение точек A и D
z D ,A
d
jy
2
D , A sin
(
d
jy )
y
y
y
y
2
sin( j ) 1 ch
j 0 sh
ch
d
2
d
d
d
d
Положение точки E
z E jy
y
y
E sin j
j sh
d
d

11.

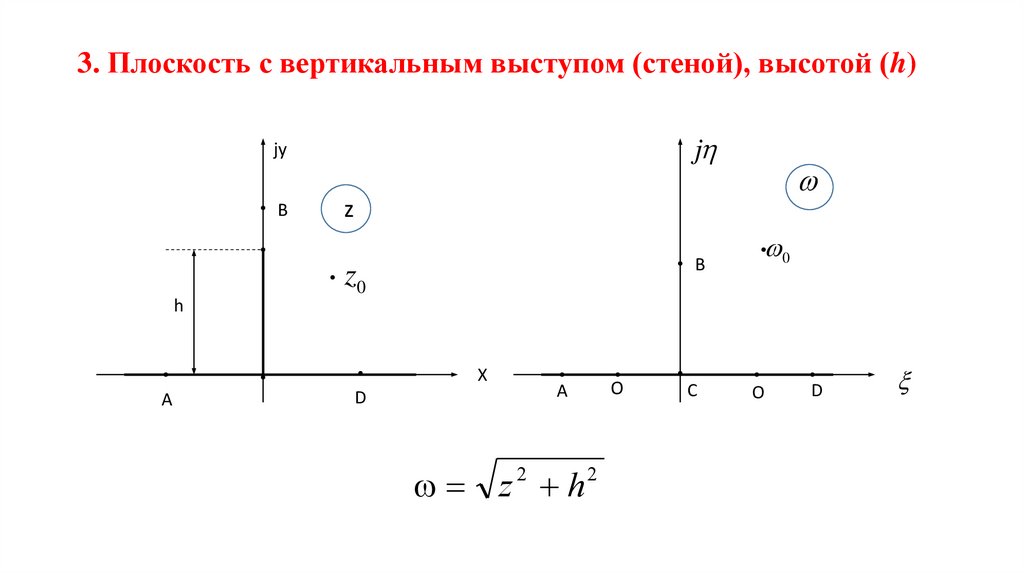
3. Плоскость с вертикальным выступом (стеной), высотой (h)
j
jy
B
z
B
z0
0
h
X
A
O
A
D
z h
2
2
C
O
D

12.

Положение точки C
z C jh
C 0
Положение точки O
0 h
z0 0
Положение точек A и D
DA x 2 h 2
z DA x
Положение точки B
z B jy
(y>h)
B j y 2 h 2

13.

Комплексный потенциал и плотность заряда ( ) на примере
плоскости с выступом
z0 = x0 + jy0
+
Координата заряженного провода
2
в плоскости Z
0 z 0 h 2 0 j 0 - координата заряженного провода + в плоскости
Используем метод зеркальных изображений
*
0 0 j 0
Координата зеркально расположенного заряда
Комплексный потенциал в системе двух зарядов
*
W ( )
0
0
j
j
ln
ln
*
2 0
2 0

14.

через Z для перехода к исходной области.
W (z)
z 2 h 2 0
j
ln
2
z 2 h 2 0
Выразим
*
Напряженность электрического поля в любой точке:
2z
2z
2
2
2
2
dW
j
2 z h
2 z h
E
2
2
dz
2 z 2 h 2 ( 0 j 0 )
z
h
(
j
)
0
0
После упрощения:
E dW
dz
j
2
z
( 2 j 0 )
z 2 h 2 ( z 2 h 2 0 ) 2 2 0 )
= D = E - плотность заряда на поверхности проводников

15.

Графический метод построения картины
плоскопараллельного поля.
При графическом построении необходимо соблюдать одновременно три условия.
1. Ортогональность линий равного потенциала и линий напряженности во всех точках их
пересечения
2. Линии напряженности должны подходить перпендикулярно к поверхности проводящих тел.
3. Ячейки ортогональной сетки, образованной линиями U = const и V = const должны быть подобны
друг другу.
+
U V
E
n a
U2
n
–
V a
= k = const
U n
a
U1
V1
V2