Похожие презентации:
Силовое поле. Работа. Энергия. Мощность
1.
СИЛОВОЕ ПОЛЕСиловое поле – форма материи,
связывающая частицы вещества в
единые системы и передающая
действие одних частиц на другие.
2.
rr
r
F
О
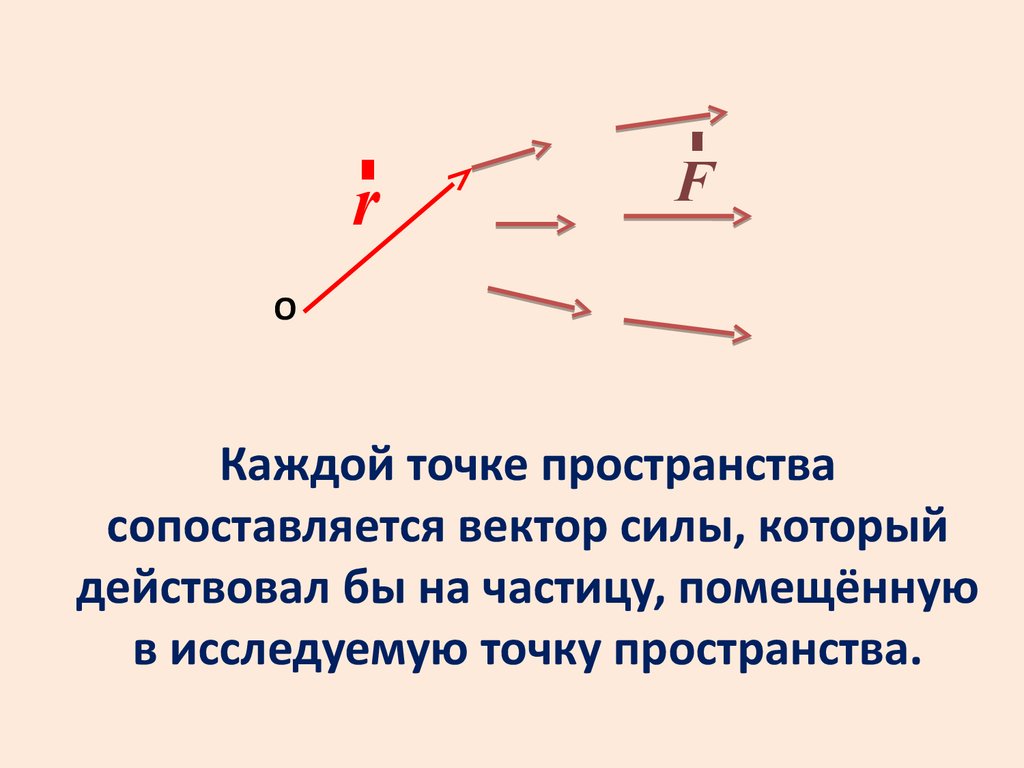
Каждой точке пространства
сопоставляется вектор силы, который
действовал бы на частицу, помещённую
в исследуемую точку пространства.
3.
Центральное силовое полеВ поле центральных сил на МТ
действуют силы, которые
направлены вдоль прямых,
проходящих через одну и ту же
точку – центр сил.
Величина этих сил зависит
только от расстояния до центра сил.
4.
rr
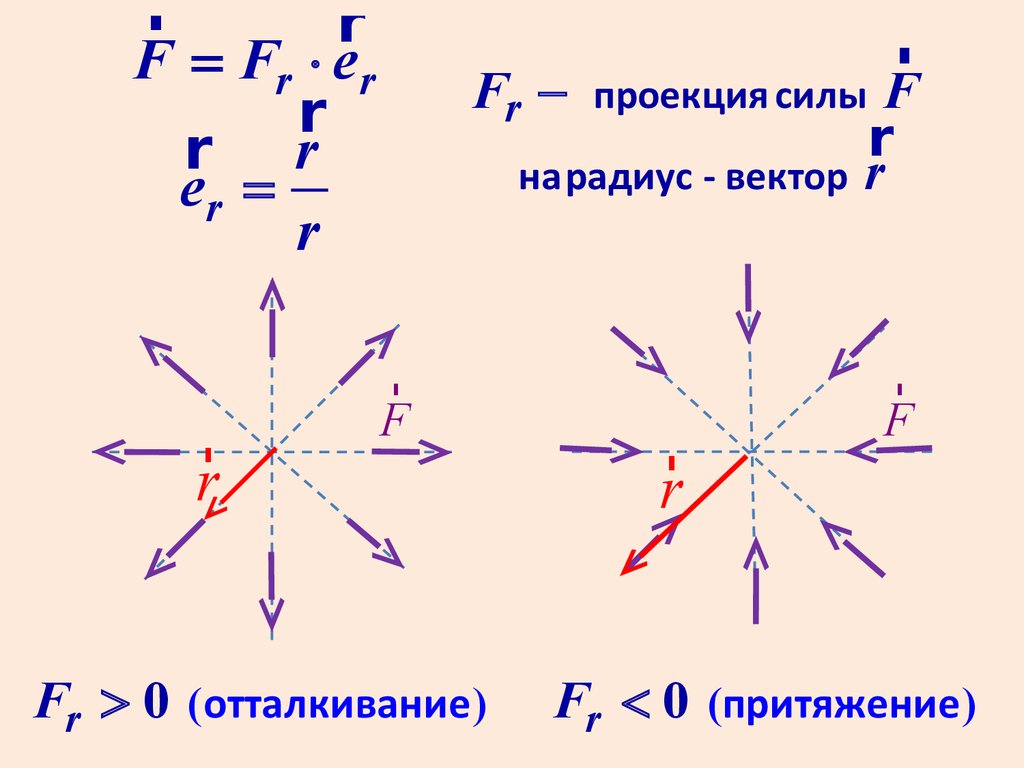
F = Fr × er
r
r r
er =
r
r
r
r
Fr - проекция силы F
r
на радиус - вектор r
r
F
Fr > 0 ( отталкивание )
r
r
r
F
Fr < 0 (притяжение)
5.
Примеры центральных сил:•Силы тяготения в гравитационном поле Земли
•Упругие силы
r
Mm r
FТ = -G 2 × er
r
r
r r
Fупр = - k × D r × er
• Кулоновские силы, создаваемые точечными
зарядами
6.
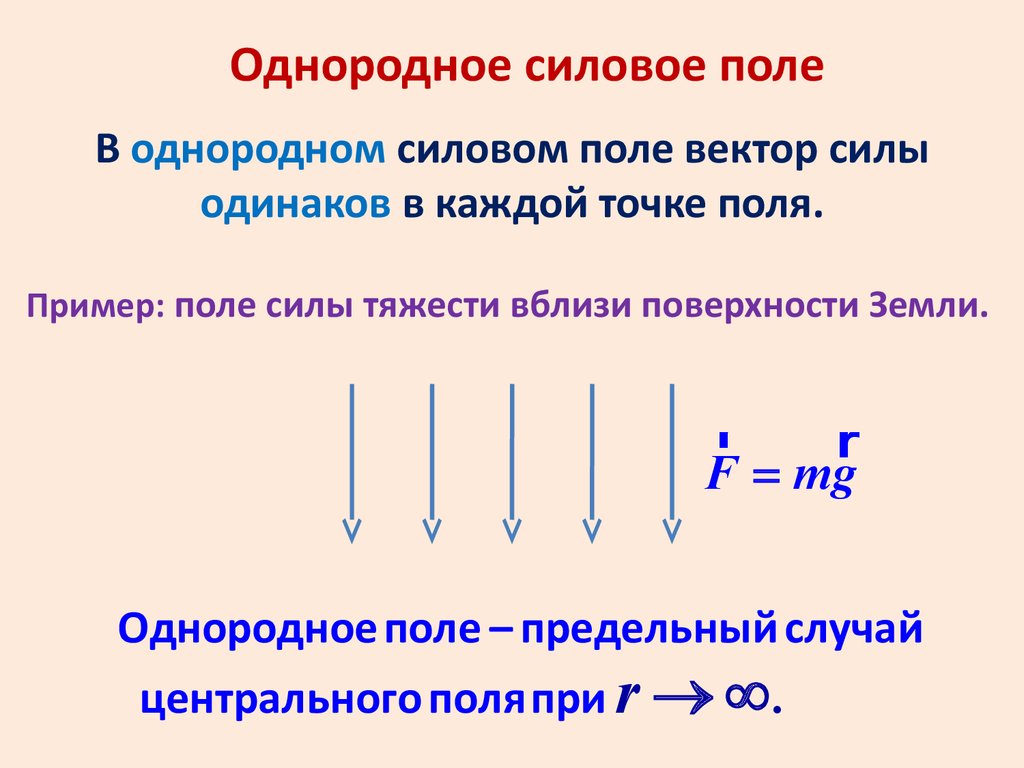
Однородное силовое полеВ однородном силовом поле вектор силы
одинаков в каждой точке поля.
Пример: поле силы тяжести вблизи поверхности Земли.
r
r
F = mg
Однородное поле – предельный случай
центрального поля при r ® ¥ .
7.
ЭНЕРГИЯЭнергия – общая мера различных
форм движения материи.
В механике это перемещение тел в
пространстве и силовое
взаимодействие между телами.
Им соответствуют кинетическая и
потенциальная энергии.
8.
РАБОТА СИЛ ПОЛЯПри превращении одной формы
движения в другую совершается
работа, равная величине перехода
энергии от одного вида к другому.
[ W ] = [ A] = [ Дж ]
9.
Механическая работаЭлементарная работа равна
скалярному произведению векторов
силы и элементарного перемещения.
r r
r
d A = ( F , dr ) = F × dr × cos a
F
d A = F × ds × cos a
a
r
dr
Ft
d A = Ft × ds
10.
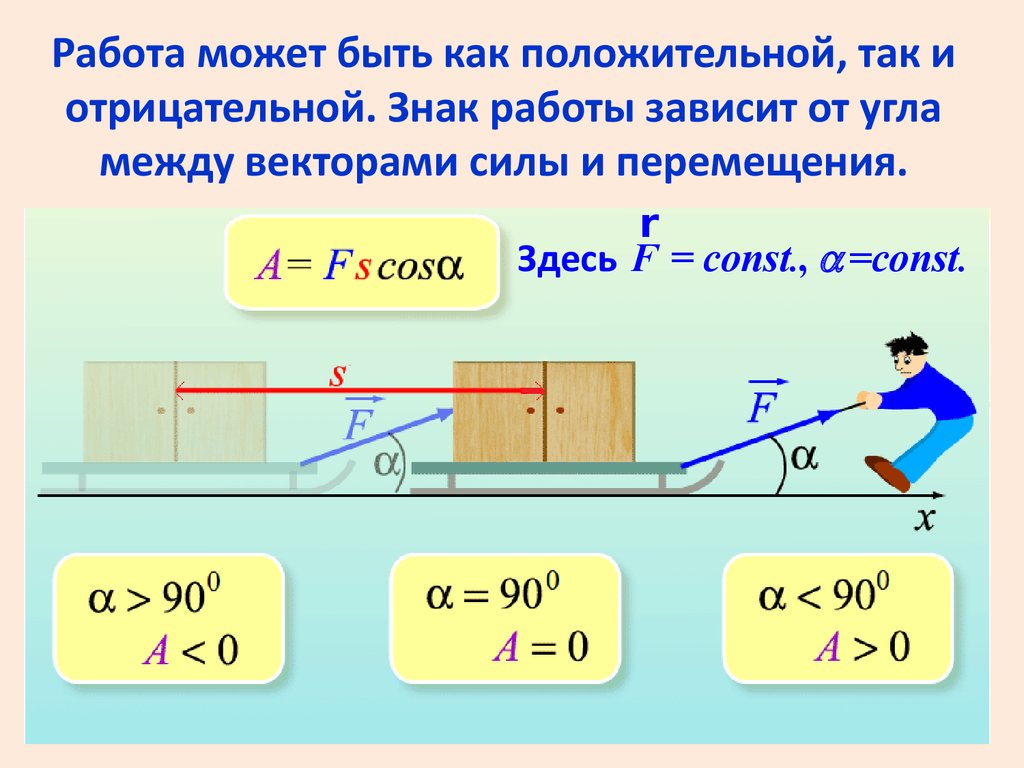
Работа может быть как положительной, так иотрицательной. Знак работы зависит от угла
между векторами силы и перемещения.
r
Здесь F = const., a =const.
11.
Полная работа переменной силы:A = ò dA
A = ò Ft ds
A = ò F ds cos a
r r
A = ò F , dr
(
)
12.
Полная работа постоянной силы:A = ò Ft ds = Ft ò ds
A = Ft × s
13.
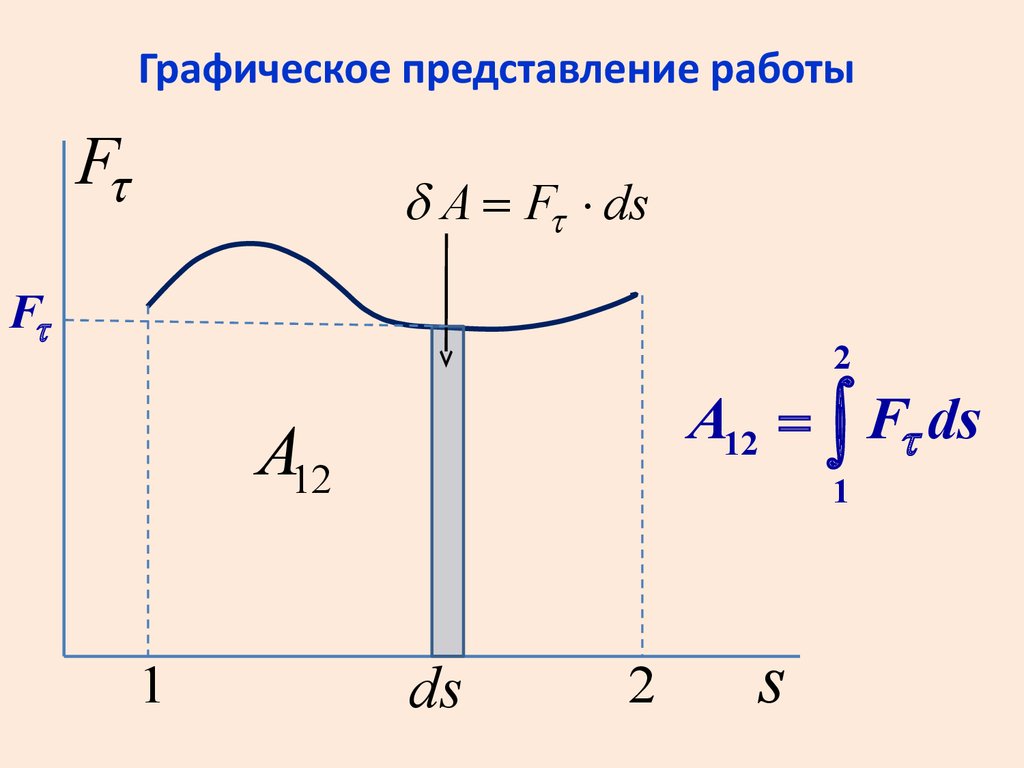
Графическое представление работыFt
d A = Ft × ds
Ft
2
A12 = ò Ft ds
A12
1
1
ds
2
s
14.
МощностьМощность равна работе, совершаемой
в единицу времени.
dA
N=
dt
Ft ds
N=
dt
r r
N = Ft v = F , v
(
[ N ] = [ Вт ]
Средняя мощность :
A
N =
t
)
15.
Потенциальные силовые поляСиловое поле называют
потенциальным, а силы,
действующие в нём,
консервативными, если работа сил
поля не зависит от вида траектории,
а зависит только от положений тела
в исходном и конечном состояниях.
16.
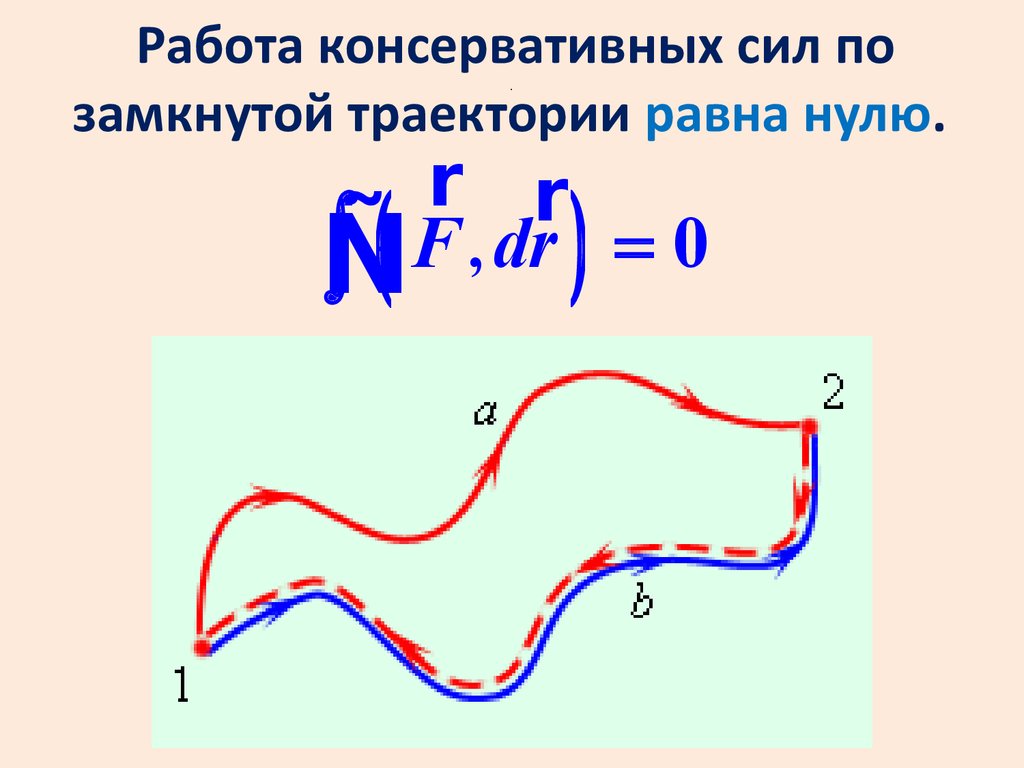
Работа консервативных сил позамкнутой траектории равна нулю.
.
r r
F
,
dr
=
0
ò
Ñ
(
)
17.
Примеры консервативных сил:• Силы тяготения
• Упругие силы
• Кулоновские силы
Все центральные силовые поля
потенциальны.
18.
Диссипативные силыСилы, работа которых зависит от
траектории движения, не являются
консервативными.
Если при действии таких сил энергия
переходит в немеханические формы,
то эти силы называют
диссипативными.
19.
Работа диссипативных сил отрицательна.Aдисс < 0
Работа этих сил по замкнутой
траектории не равна нулю.
r
r
F
,
dr
¹
0
ò дисс
Ñ
(
)
20.
Примеры диссипативных сил:•Силы трения скольжения
•Силы сопротивления
среды
π
r
r
A= Ñ
F
,
dr
<
0
тр
ò
(
)
21.
Кинетическая энергияЭнергию, которой
обладают движущиеся
тела, называют
кинетической .
Обозначим: Wk.
22.
Пусть на МТ действует сила. Найдем ее работу.d A = Ft ds = ( m × at ) ( v × dt )
dv ö
æ
d A = ç m × ÷ ( v × dt )
dt ø
è
2
æ mv ö
d A = mv × d v = d ç
÷
2
è
ø
23.
Работа равна приращению величины вскобках. Это кинетическая энергия.
æ mv ö
d A= dç
÷ = dWk
è 2 ø
2
mv
Wk =
2
2
24.
Изменение кинетической энергиитела равно работе
равнодействующей силы.
Wk 2 - Wk 1 = A12
25.
Потенциальная энергияПотенциальная энергия – это
энергия взаимодействия тел.
Обозначим: WП.
26.
Потенциальная энергиятела в силовом поле
Силы поля, перемещая тело, совершают
работу, равную убыли потенциальной энергии:
dWП = -d A
r r
dWП = - F × dr
27.
При перемещении из точки 1 в точку 2WП 2 - WП1 = - A12
Формула WП определяется видом
силового взаимодействия
Wп = - ò
(
r r
F , dr
)
28.
Потенциальная энергия телав поле силы тяжести
y1
1
y0
y2
Wп
r
mg
0
2
А = Ft s = mg ( y1 - y2 )
A = Wп1 - Wп2
Wп = mgy + C
29.
ВыберемWп ( y0 ) = 0
Тогда
C = - mgy0
Wп = mg ( y - y0 )
30.
Потенциальная энергия упругих силWп = - ò
(
r r
F , dr = - ò Fx dx
)
По закону Гука
Fx = - kx
31.
2kx
Wп = ò kxdx =
+C
2
Выберем WП(0)=0, тогда С=0 и
kx
Wп =
2
2
32.
Связь силы и потенциальной энергииГрадиент скалярного поля
Скалярным полем называют
область пространства, каждая
точка которого характеризуется
некоторой скалярной
величиной, например,
потенциальной энергией.
33.
rdr
r
F
Поверхностью уровня
скалярного поля
называют
совокупность точек
пространства, в
которых скалярная
величина имеет одно
и то же значение.
Силы поля перпендикулярны к
поверхности уровня WП.
34.
Вектор градиента скалярного поля:dW П r
grad W П =
n
dn
r
n - единичный вектор нормали
к поверхности уровня, направленный
в сторону роста скалярной величины
35.
Градиент скалярного поля– это вектор, по модулю равный
изменению скалярной величины на
единицу длины в направлении
нормали к поверхности уровня.
Направлен вектор градиента
перпендикулярно поверхности уровня
в сторону возрастания этой скалярной
величины.
36.
В координатной форме¶Wп r ¶Wп r ¶Wп r
gradWп =
i +
j+
k
¶x
¶y
¶z
Оператор набла
¶ r ¶ r ¶ r
Ñ=
i+
j+ k
¶x
¶y
¶z
37.
Связь консервативной силы ипотенциальной энергии
r
F = - gradW П
или
r
F = -ÑW П
38.
В проекциях на оси¶WП
Fx = ¶x
¶WП
Fy = ¶y
¶W П
Fz = ¶z
39.
Потенциальная энергиявзаимодействия системы тел
Потенциальная энергия взаимодействия
– это величина, равная работе,
совершаемой силами взаимодействия тел
при изменении расположения тел из
данного состояния в состояние, в котором
потенциальная энергия взаимодействия
условно принимается равной нулю.
40.
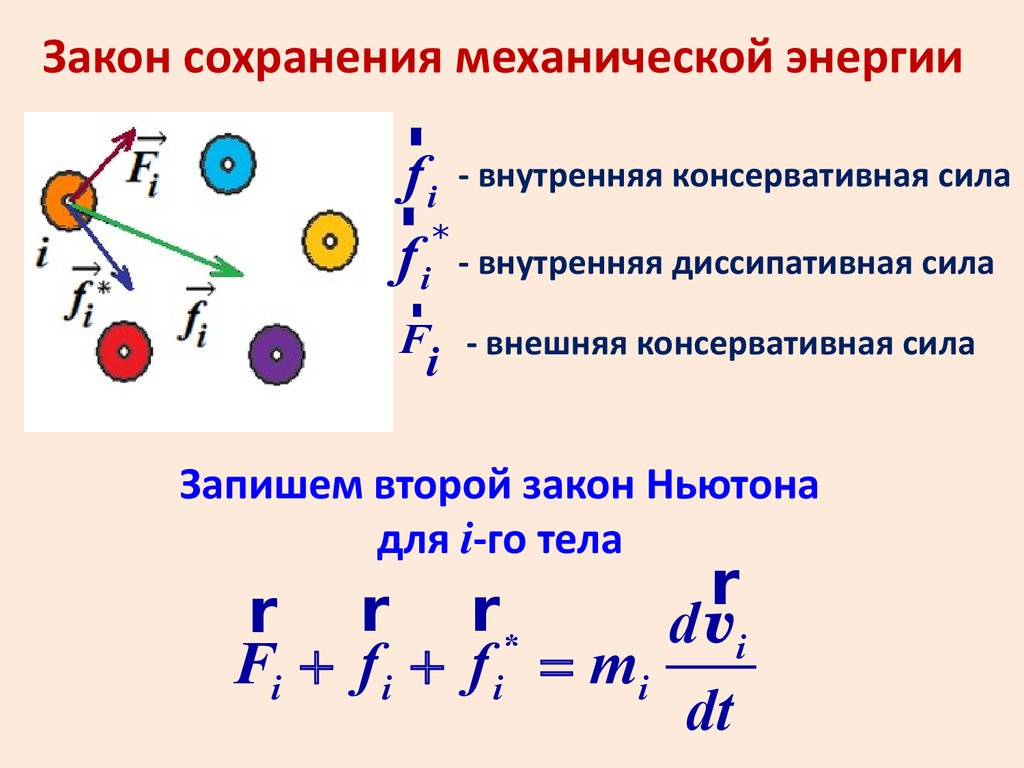
Закон сохранения механической энергииr
f i - внутренняя консервативная сила
r*
f i - внутренняя диссипативная сила
r
F - внешняя консервативная сила
i
Запишем второй закон Ньютона
для i-го тела
r
r r r*
d vi
Fi + f i + f i = mi
dt
41.
Умножим скалярно обе части равенства наперемещение тела.
Учитывая,
(
r r
что dri = vi dt
r r
r* r
r r
Fi , dr + f i , dr + f i , dr
получим :
r r
= mi ( vi , d vi )
) (
) (
)
r r
r r
r r
æmv
( F , dr ) + ( f , dr ) + ( f , dr ) = d ç 2
i
i
i
*
i
i
i
i
i
i
i
è
2
i
ö
÷
ø
Сложим для всех тел:
n
å(
i =1
n
n
n
r r
r* r
r r
æ mi vi2 ö
Fi , dri + å f i , dri + å f i , dri = å d ç
÷
i =1
i =1
i =1
è 2 ø
)
(
)
(
)
42.
nå(
i =1
2
n
n
n
r r
r* r
r r
æ mi vi ö
Fi , dr + å f i , dri + å f i , dr = å d ç
÷
i
i
i =1
i =1
i =1
è 2 ø
)
(
)
(
)
Работа сил
Работа дисси- Изменение
Работа
сил
внешнего
пативных сил кинетической
взаимодействия
потенциального
энергии
поля
- dW П ,внеш - dW П , взаим + d A = dWk
*
d A = d (WkП+внеш
W
*
,
+W
П взаим ,
)
43.
Полная механическая энергиясистемы тел:
W = WkП+внеш
W
,
+W
П взаим ,
или
W = WkП+ W
44.
Закон изменения механическойэнергии системы тел
Изменение механической
энергии системы тел равно
работе диссипативных сил.
dW = d A
*
45.
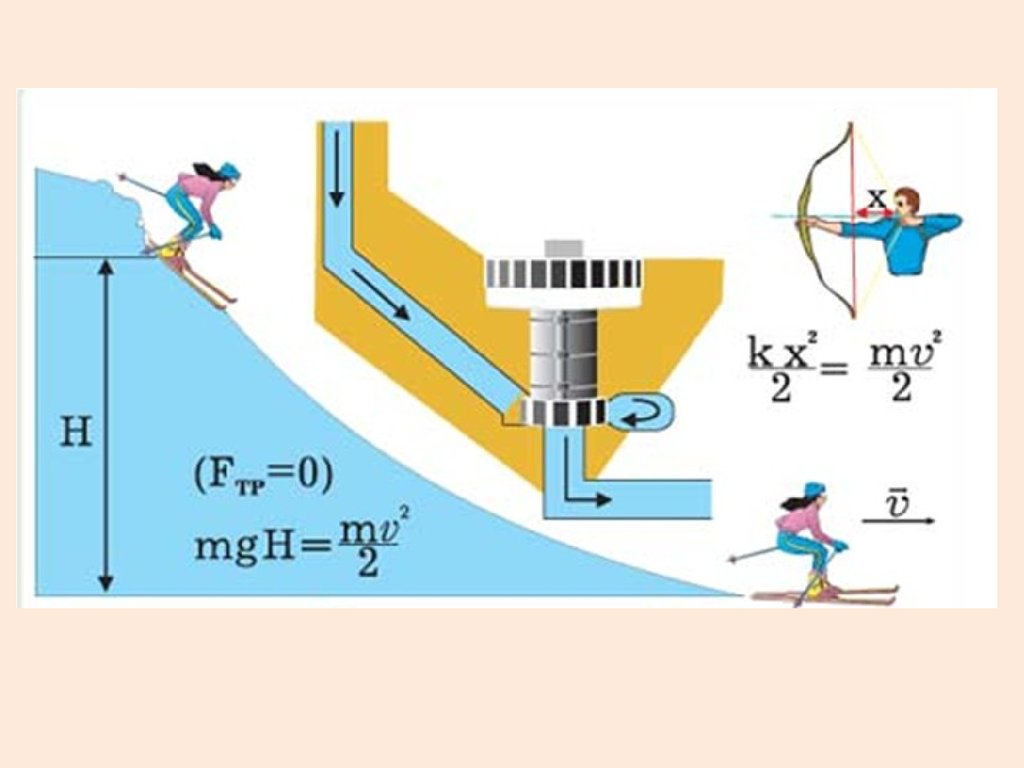
Закон сохранения механическойэнергии системы тел
В системе, на тела которой
действуют только консервативные
силы, механическая энергия не
изменяется.
46.
47.
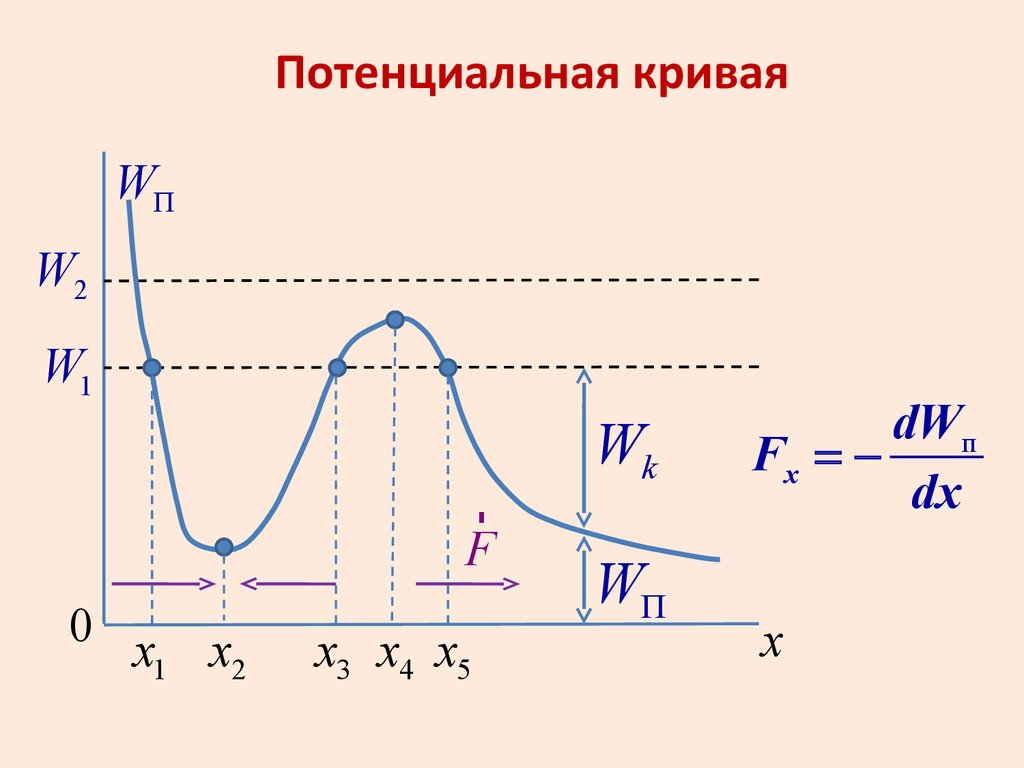
Потенциальная криваяWП
W2
W1
r
F
0
x1 x2
x3 x4 x5
Wk
WП
dWп
Fx = dx
x
48.
Соударение телПри соударении тел их
взаимодействие длится очень
короткое время. Поэтому силы
взаимодействия тел
r
r
Dp
F =
Dt
велики, и внешними силами
часто можно пренебречь.
49.
При ударе систему тел можносчитать квазизамкнутой.
В такой системе тел выполняется
закон сохранения импульса.
50.
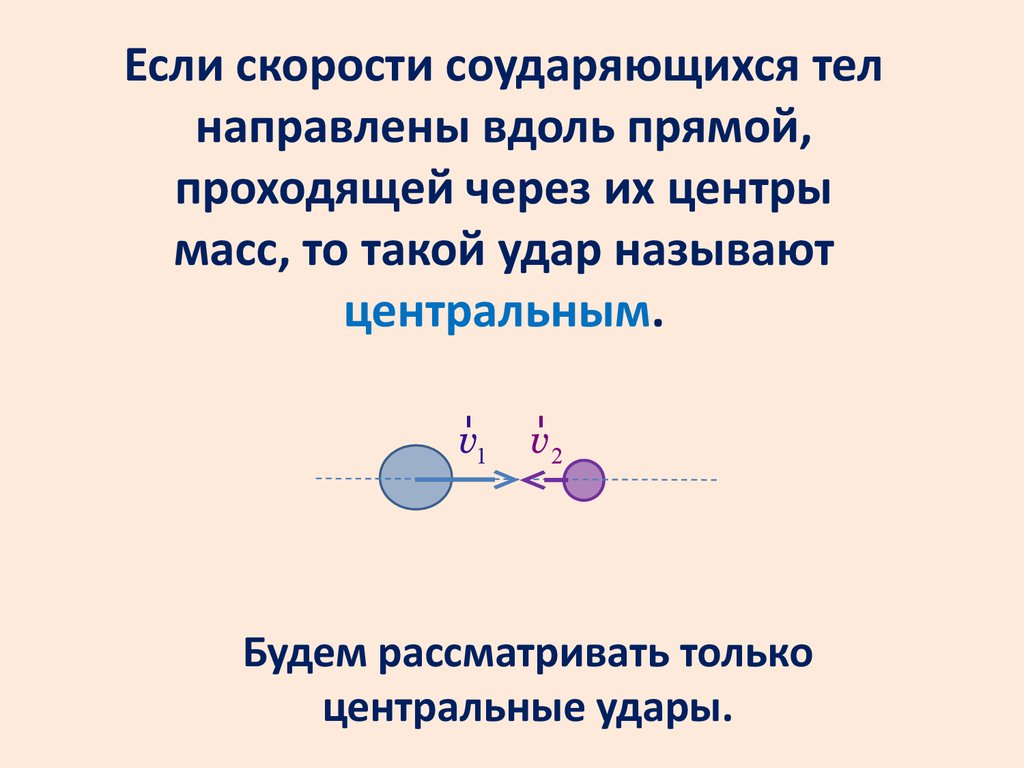
Если скорости соударяющихся телнаправлены вдоль прямой,
проходящей через их центры
масс, то такой удар называют
центральным.
r
v1
r
v2
Будем рассматривать только
центральные удары.
51.
Виды удараЕсли при ударе не происходит
перехода энергии в
немеханические формы (ε=1),
то такой удар называют
абсолютно упругим.
В этом случае выполняется
закон сохранения
механической энергии.
52.
Если при ударе тела слипаются идвижутся дальше как единое целое
(ε=0), то такой удар называют
абсолютно неупругим.
В этом случае механическая энергия
полностью или частично переходит в
немеханическую форму.
53.
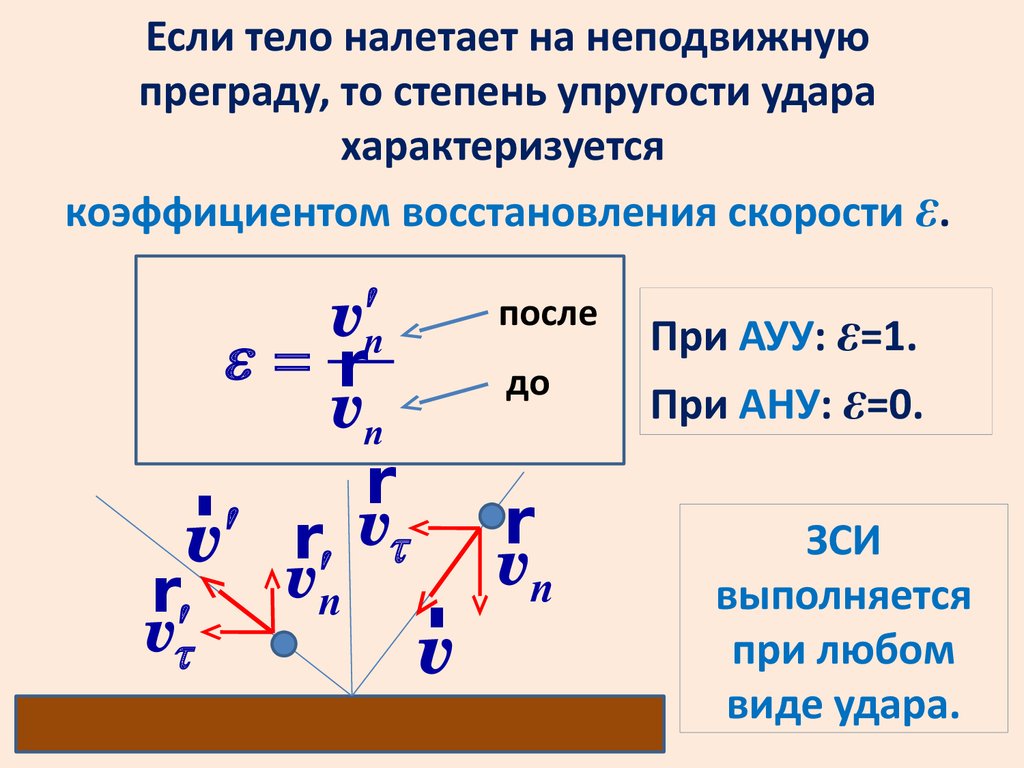
Если тело налетает на неподвижнуюпреграду, то степень упругости удара
характеризуется
коэффициентом восстановления скорости ε.
e
r
v¢
r
vt¢
после
vn¢
= r
до
vn
r
r vt vr
vn¢ r n
v
При АУУ: ε=1.
При АНУ: ε=0.
ЗСИ
выполняется
при любом
виде удара.
54.
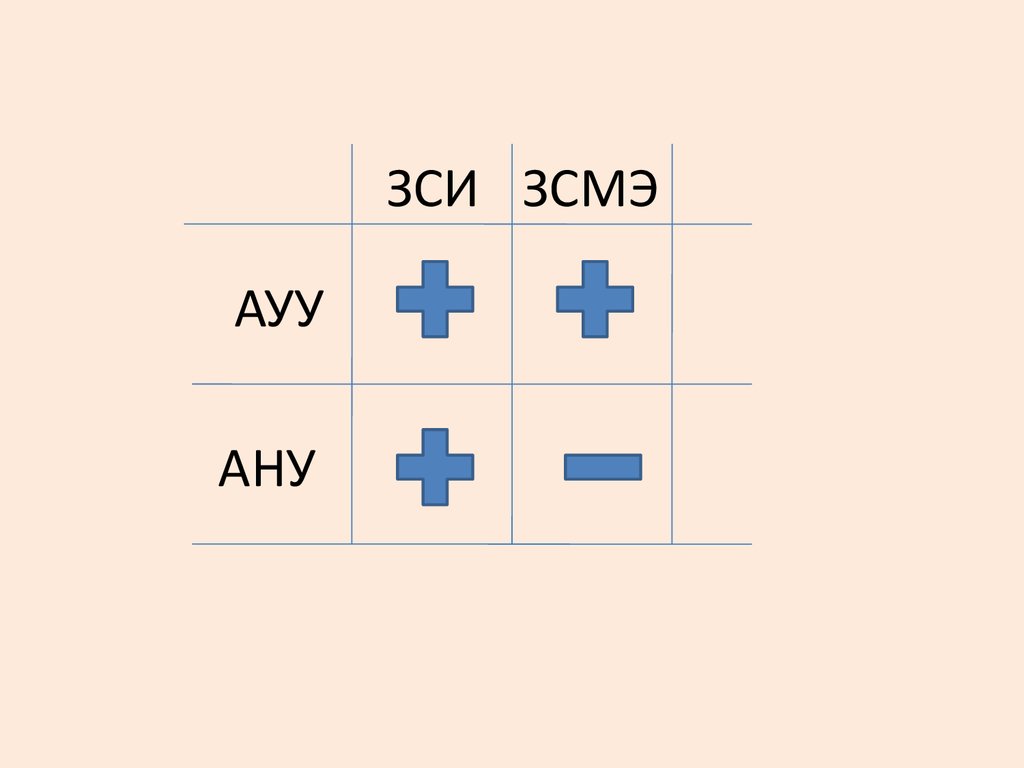
ЗСИ ЗСМЭАУУ
АНУ
55.
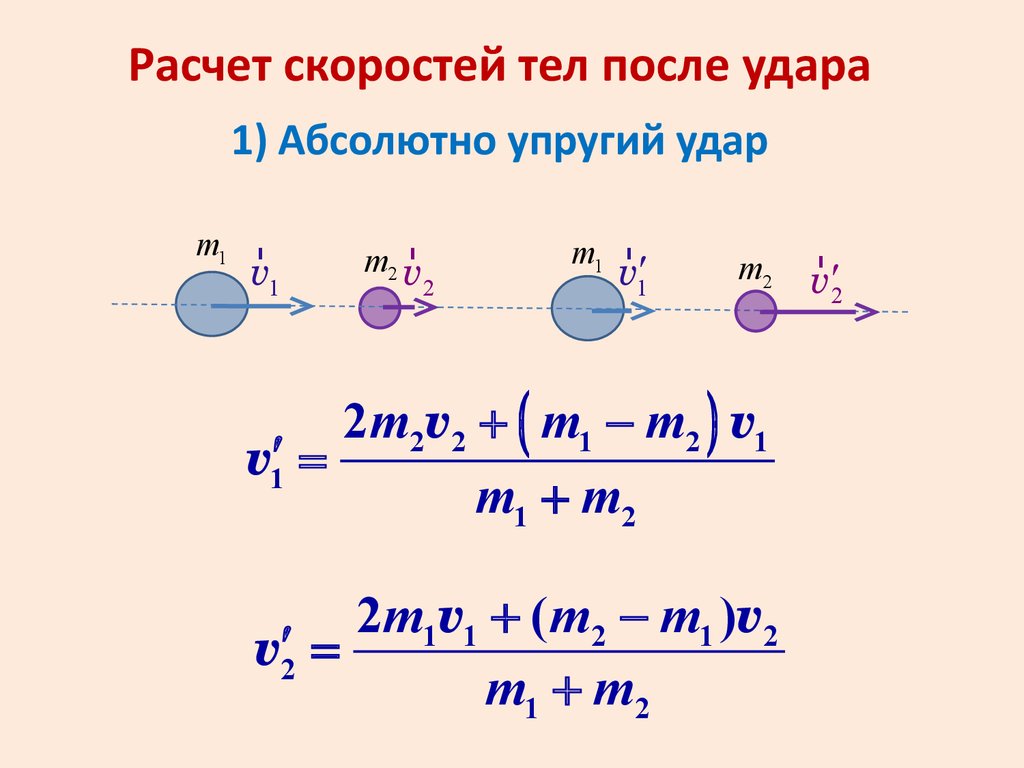
Расчет скоростей тел после удара1) Абсолютно упругий удар
m1 r
v1
m2 vr
2
m1 r
v1¢
m2
2m2v2 + ( m1 - m2 ) v1
v1¢ =
m1 + m2
2m1v1 + ( m2 - m1 )v2
v¢2 =
m1 + m2
r
v¢2
56.
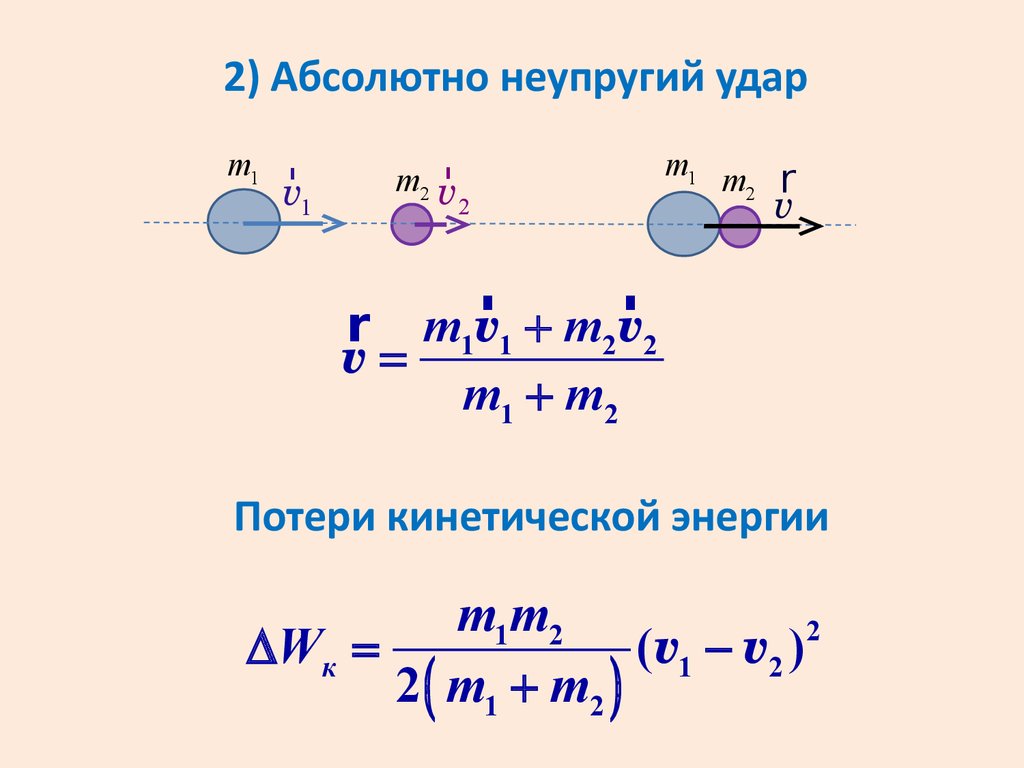
2) Абсолютно неупругий ударm1 r
v1
m2 vr
2
m1 m r
2
v
r
r
r m1v1 + m2v2
v=
m1 + m2
Потери кинетической энергии
m1m2
2
DWк =
(v1 - v2 )
2 ( m1 + m2 )

















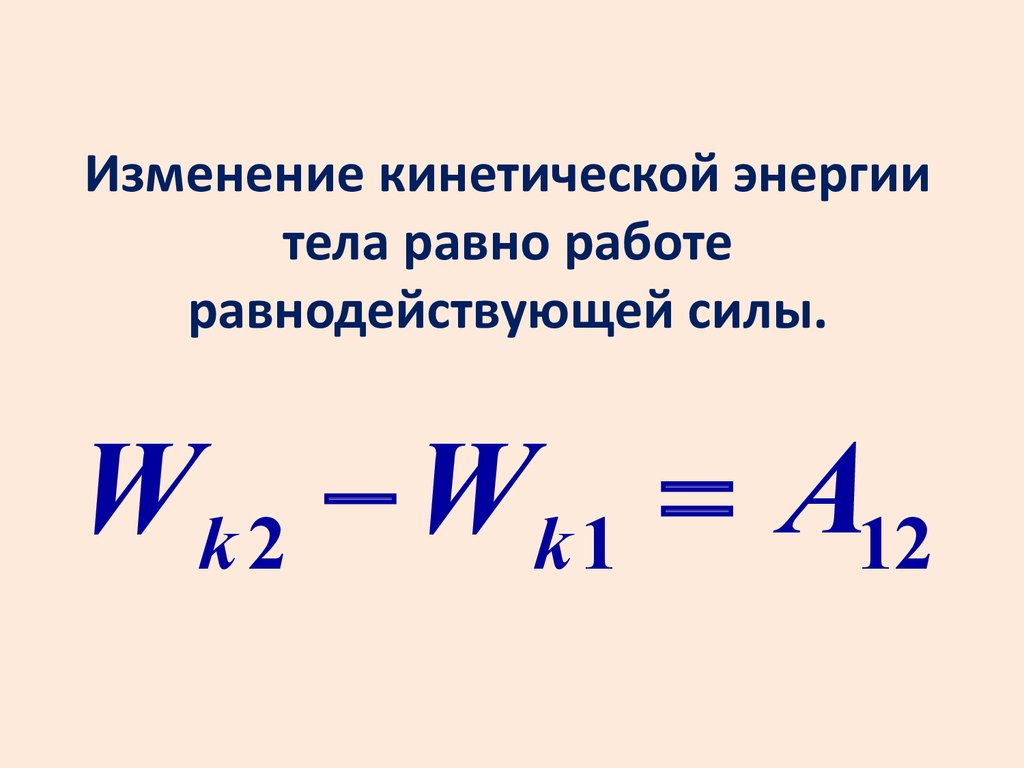






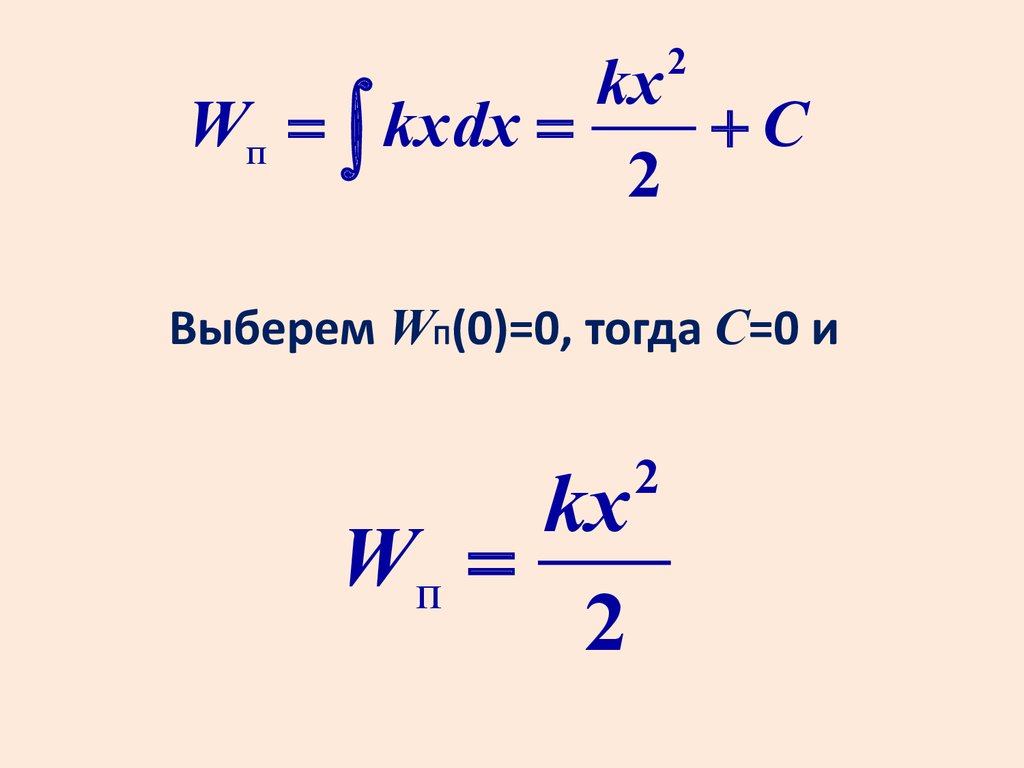

















 Физика
Физика








