Соотношение между сторонами и углами треугольника

1.

2.

Устная работа:
1. Сумма углов треугольника равна…
2. Треугольник называется прямоугольным, если…
3. Сторона прямоугольного треугольника, лежащая против
прямого угла, называется ….
4. Катет – это …
5. Прямым называется угол равный …
6. Если градусная мера угла меньше 900 он называется …

3.

Устная работа:
Назовите:
R
Гипотенузу треугольника OPR
Катет противолежащий R
O
P
Катет прилежащий O
Гипотенузу треугольника MKL
M
Катет противолежащий M
К
Катет прилежащий к K
L

4.

Теорема о соотношении между сторонами и углами
треугольника
В треугольнике:
1) против большей стороны лежит больший угол; и обратно
2) против большего угла лежит большая сторона.
X
Напротив большего угла Х,
МО – большая сторона
Напротив меньшего угла О,
меньшая сторона МХ
М
O

5.

А
А
Доказательство:
D
В
С
В
2
1
С
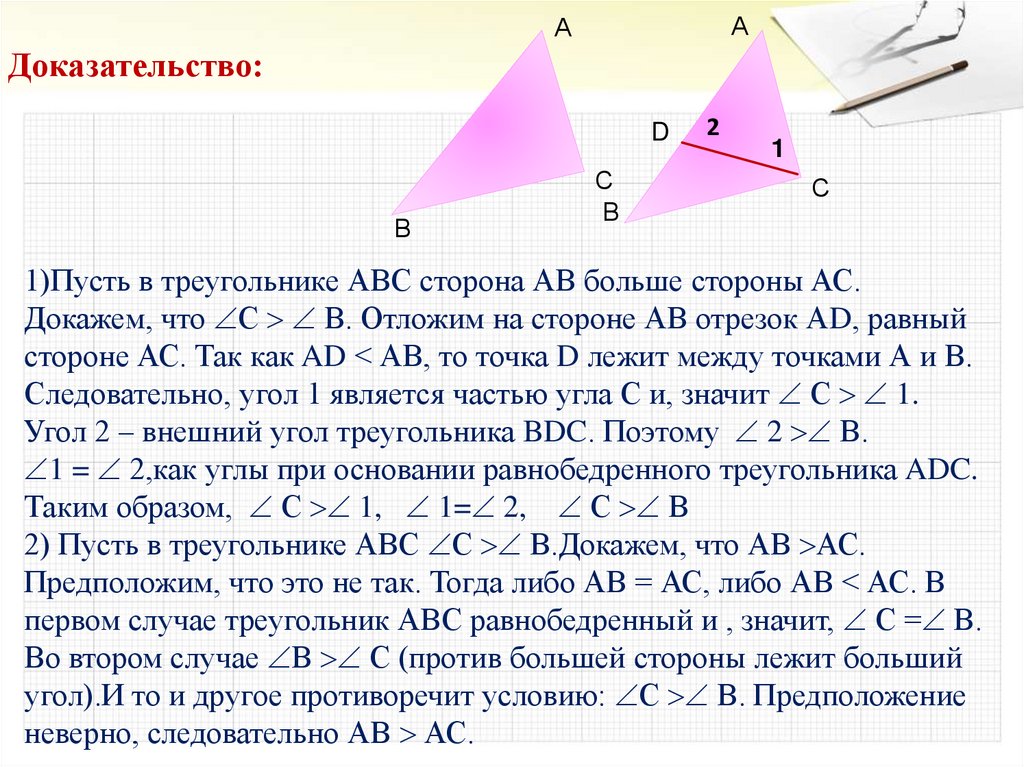
1)Пусть в треугольнике АВС сторона АВ больше стороны АС.
Докажем, что С В. Отложим на стороне АВ отрезок АD, равный
стороне АС. Так как AD < АВ, то точка D лежит между точками А и В.
Следовательно, угол 1 является частью угла С и, значит С 1.
Угол 2 – внешний угол треугольника BDC. Поэтому 2 В.
1 = 2,как углы при основании равнобедренного треугольника ADC.
Таким образом, С 1, 1= 2, С В
2) Пусть в треугольнике АВС С В.Докажем, что АВ АС.
Предположим, что это не так. Тогда либо АВ = АС, либо АВ < АС. В
первом случае треугольник АВС равнобедренный и , значит, С = В.
Во втором случае В С (против большей стороны лежит больший
угол).И то и другое противоречит условию: С В. Предположение
неверно, следовательно АВ АС.

6.

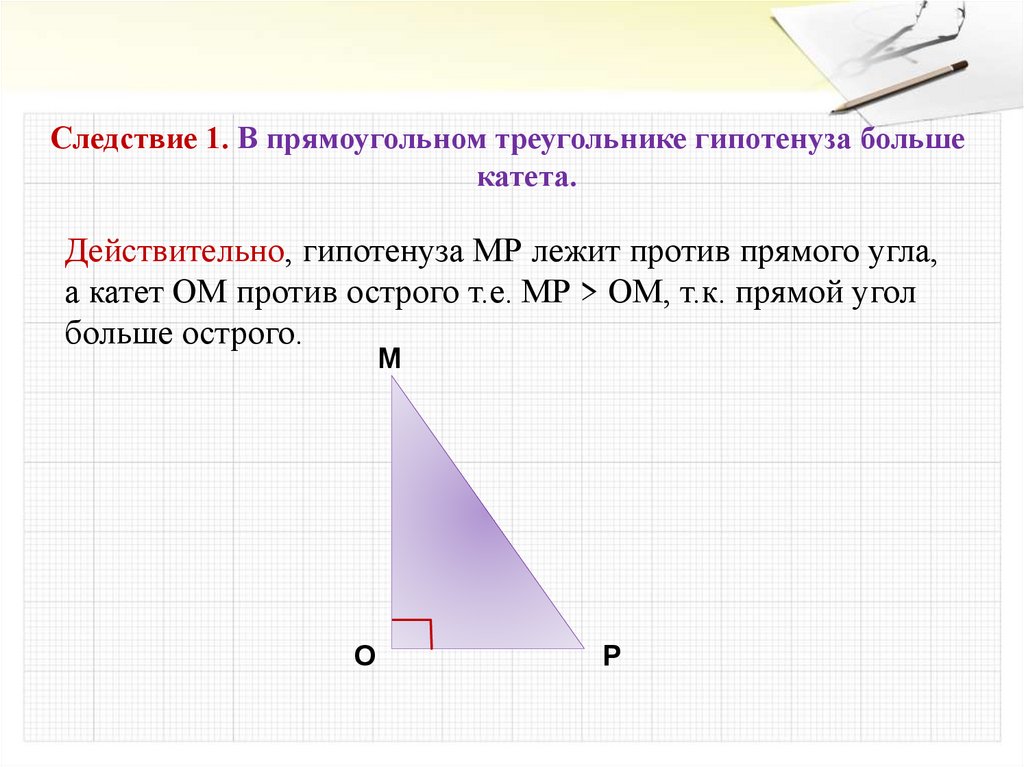
Следствие 1. В прямоугольном треугольнике гипотенуза больше
катета.
Действительно, гипотенуза МР лежит против прямого угла,
а катет ОМ против острого т.е. МР > ОМ, т.к. прямой угол
больше острого.
М
О
Р

7.

Следствие 2. Если два угла треугольника равны, то треугольник
равнобедренный.
Доказательство: Пусть в треугольнике АВС два угла равны. Тогда
равны и стороны лежащие против этих углов. Если предположить, что
одна из указанных сторон больше другой, то угол, лежащий против
неё, будет больше угла, лежащего против другой стороны, а это
противоречит условию. Итак, в треугольнике две стороны равны, т.е.
треугольник равнобедренный.
А
В
С

8.

Теорема: Каждая сторона треугольника меньше
суммы двух других сторон.
Доказательство: Рассмотрим произвольный, треугольник АВС докажем ,
что АВ< АС + СВ. Отложим но продолжении стороны АС отрезок CD,
равный стороне СВ. В равнобедренном треугольнике BCD 1= 2, в
треугольнике ABD ABD 1,
и значит, ABD 2.Так как в треугольнике против большего угла
лежит большая сторона, то АВ < AD.
Но AD = АС + СD = AC + CB, поэтому АВ < АС + СВ.
В
1
2
А
С
D

9.

Для любых трёх точек А,В,С не лежащих на одной
прямой, справедливы неравенства:
АВ < АС + СВ
АС < АВ + ВС
ВС < ВА + АС
Каждое из этих неравенств называется
неравенством треугольника

10.

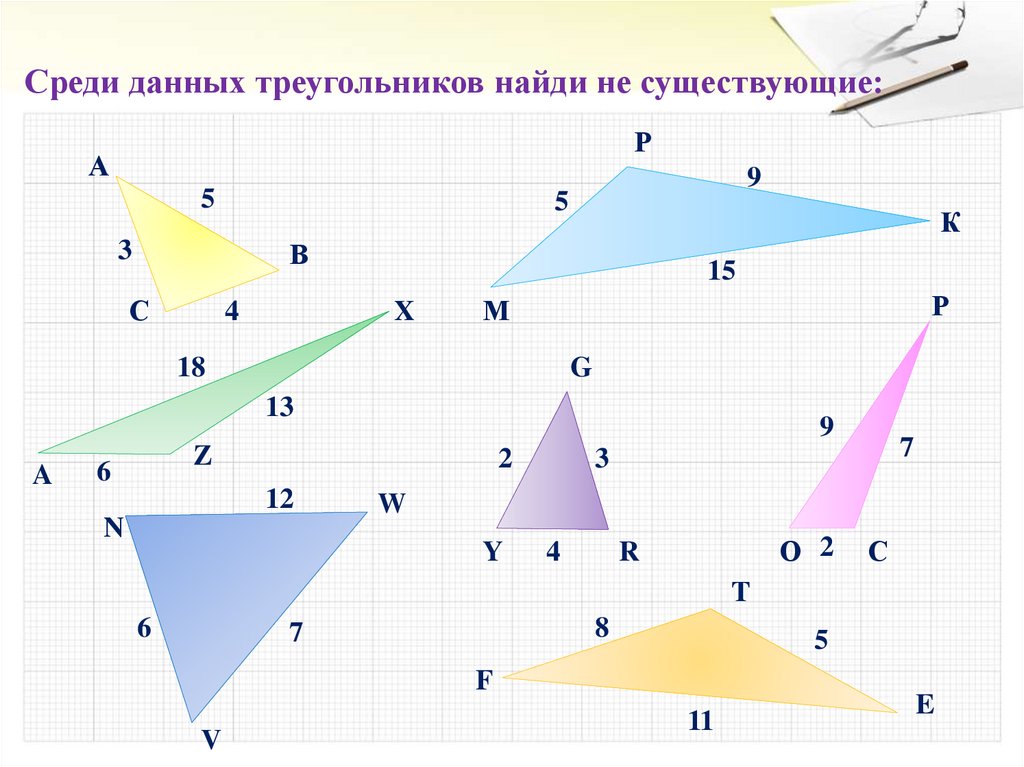
Среди данных треугольников найди не существующие:
Р
А
5
9
5
К
В
3
С
4
15
X
Р
М
18
G
13
A
9
Z
6
2
12
N
7
3
W
Y
4
О 2
R
С
T
6
8
7
5
F
V
11
E