Преобразование графиков функций. 9 класс

1.

Преобразование
графиков функций
9 класс

2.

Цель: показать наглядно преобразование графиков
известных функций,
применение преобразования графиков для построения
графиков кусочно-заданных функций, содержащих
знак модуля

3.

Симметрия относительно оси Ох
у
у= х²
0 1
у= -х²
х
Точка пересечения
графика с осью Ох
остается
неизменной

4.

Симметрия относительно оси Ох
у
у х
х
0 1
у х
Точка пересечения графика с осью Ох остается неизменной

5.

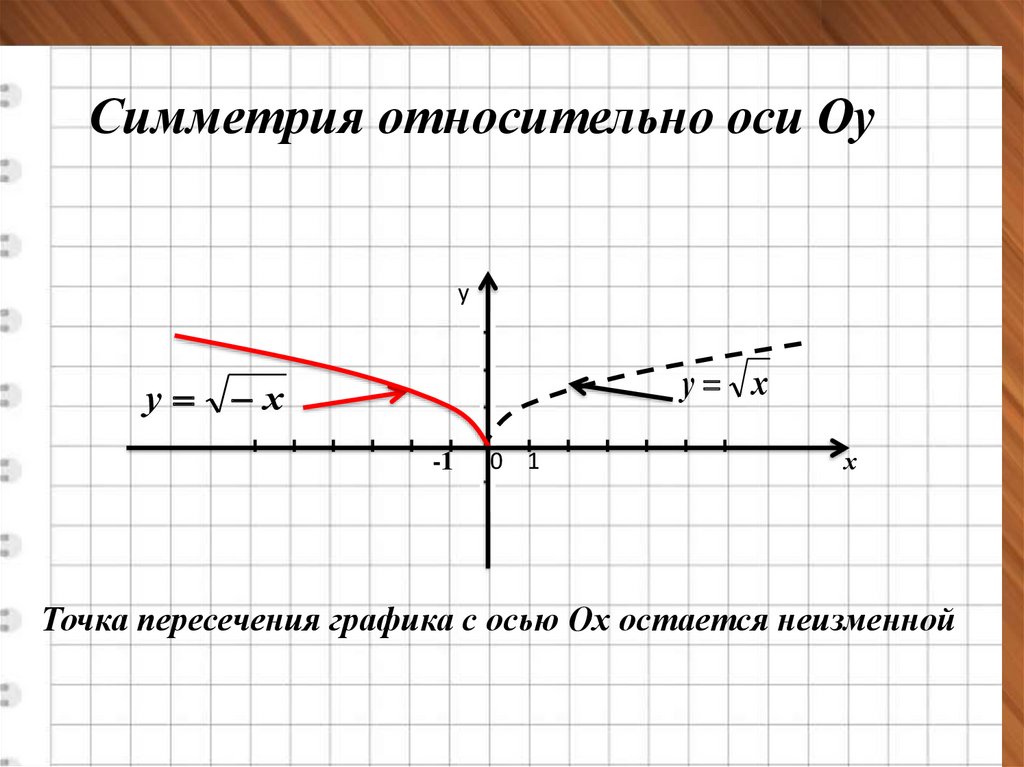
у
Симметрия относительно оси Оу
у= х²
у
у
х
у х
0 1
-1 0 1
х
х
у= -х²
Точка пересечения графика с осью Ох остается неизменной

6.

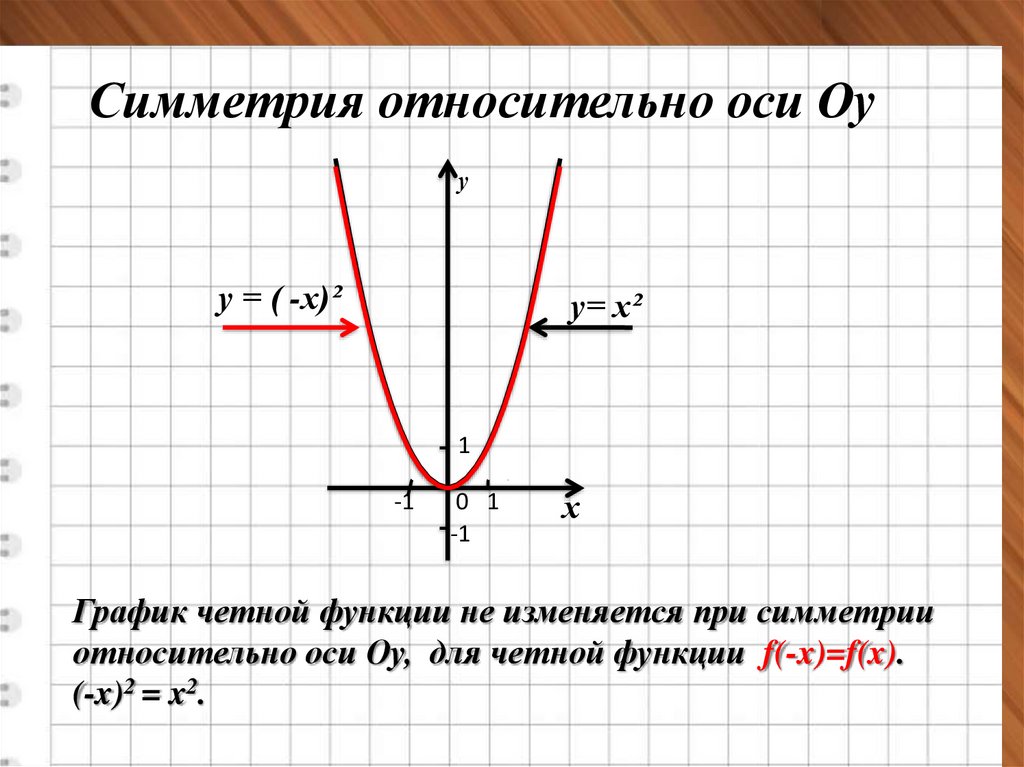
Симметрия относительно оси Оу
у
у = ( -х)²
у= х²
1
-1
0 1
-1
х
График четной функции не изменяется при симметрии
относительно оси Оу, для четной функции f(-x)=f(x).
(-x)2 = x2.

7.

Сдвиг
по оси Ох
у
у х 6
2
у х 6
у= х²
-6
0 1
y=f(x-a)- сдвиг вправо, a>0
y=f(x+a) –сдвиг влево, a>0
2
6
х

8.

Сдвиг
по оси Ох
у
1).
2
у
2).
х 3
2
у
х
-
сдвиг графика
№1 вправо на
3 ед.
2
у
х
х
0 1
у
2
х 3

9.

Сдвиг
по оси Ох
у
у
у х
х 5
у х 1
-5
0 1
y=f(x+a) –сдвиг влево, a>0
y=f(x-a)- сдвиг вправо, a>0
х

10.

Сдвиг
по оси Оу
у
у = х²+3
3
0 1
у= х²-3
y=f(x)+а - сдвиг вверх, a>0
х
-3
y=f(x)-а – сдвиг вниз, a>0

11.

Сдвиг
по оси Оу
у
2
1). у
х
2
2). у 2 х
5
сдвиг графика
№1 вниз вдоль
оси Оу на 2 ед.
4
2
у
х
3
2
1
-5
-4
-3
-2
-1
0 1
2
3
4
5
-1
-2
-3
-4
-5
2
у 2
х
х

12.

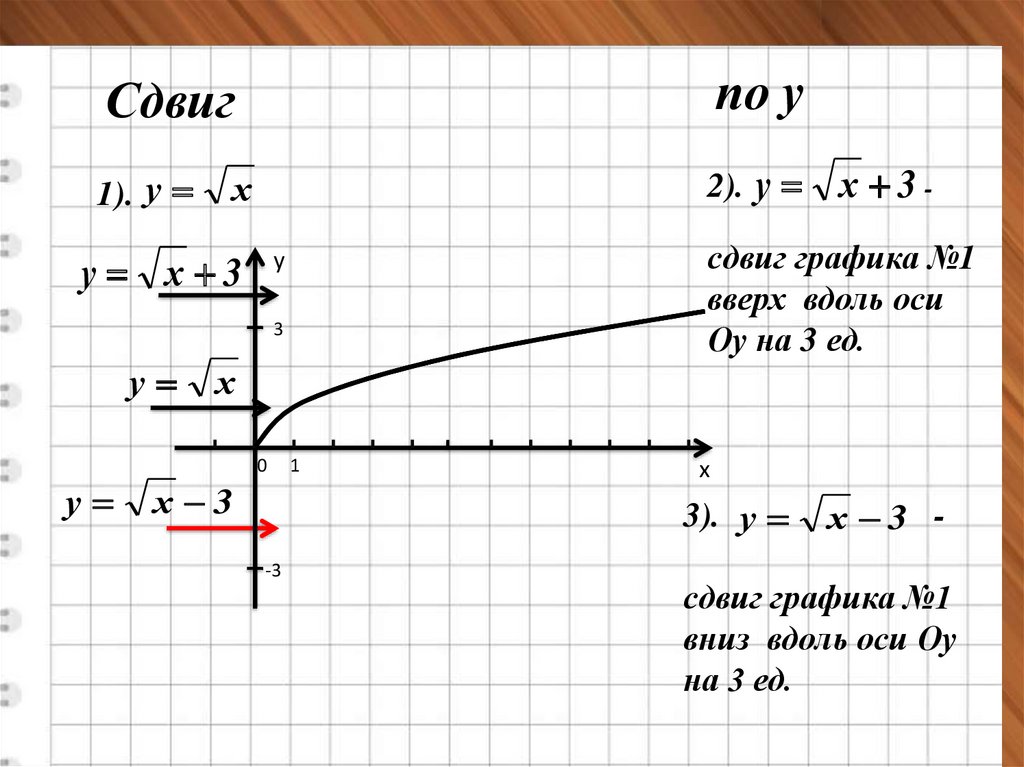
Сдвиг
по у
1). у
2). у
х
у х 3
сдвиг графика №1
вверх вдоль оси
Оу на 3 ед.
у
3
у
х
0
у
х 3-
х 3
1
х
3). у
-3
х 3 -
сдвиг графика №1
вниз вдоль оси Оу
на 3 ед.

13.

Построение графика у=kf(x)
у
у=0,5х²
у= х²
у=8х²
у=2х²
у
1 2
х
8
х
0 1
k>1- растяжение графика у=f(x) вдоль оси Оу в k раз,
1
0<k<1 -сжатие графика у=f(x) вдоль оси Оу в раз.
k

14.

Построение графика у=kf(x)
k>1- растяжение
графика у=f(x)
вдоль оси Оу в k
раз,
у
8
у х
у 3х
7
6
5
4
1
у х
2
3
0<k<1 -сжатие
графика у=f(x)
вдоль оси Оу в 1
k
раз.
2
1
-5
-4
-3
-2
-1
0 1
-1
-2
-3
2
3
4
5
6
х

15.

Построение графика у=f(kx)
у 2х
y
2
у
х
у
х
2
1
0
1
х
2
k>1- cжатие графика
у=f(x) вдоль оси Ох в k раз,
0<k<1 –растяжение графика
у=f(x) вдоль оси Ох в 1
k
раз.

16.

Сдвиг
по оси Ох и по оси Оу
у х 5 3
2
у
у= х²
3
0 1
у х 5
2
5
х

17.

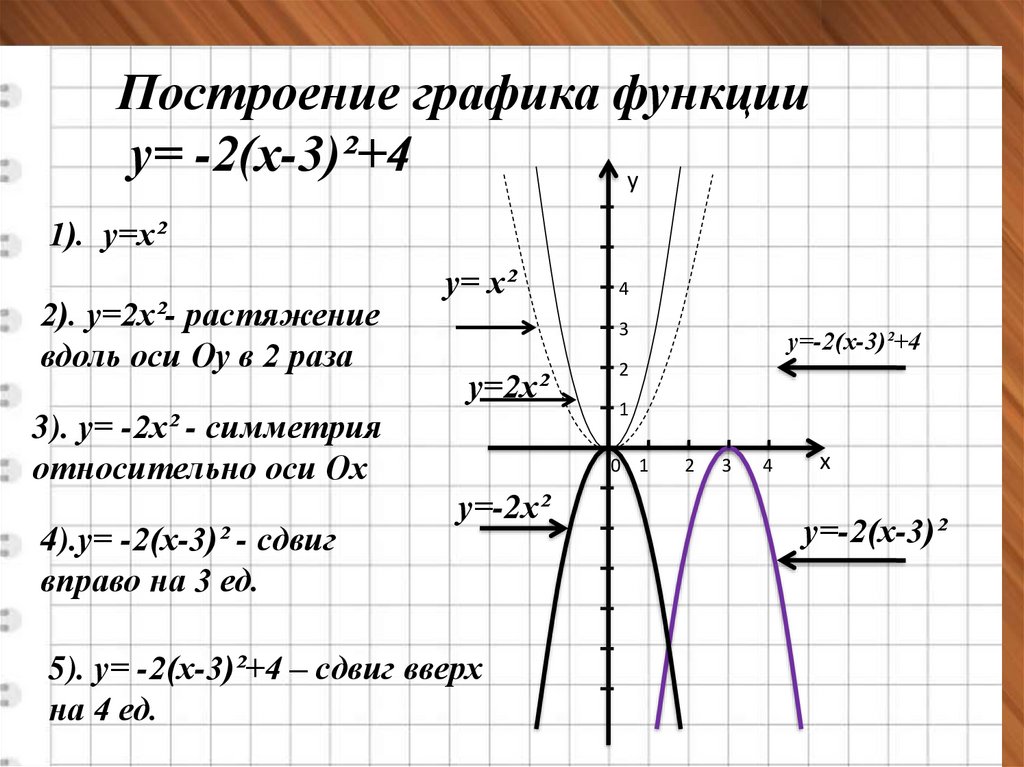
Построение графика функции
у= -2(х-3)²+4
у
1). у=х²
2). у=2х²- растяжение
вдоль оси Оу в 2 раза
у= х²
3
у=2х²
3). у= -2х² - симметрия
относительно оси Ох
4).у= -2(х-3)² - сдвиг
вправо на 3 ед.
4
2
1
0 1
у=-2х²
5). у= -2(х-3)²+4 – сдвиг вверх
на 4 ед.
у=-2(х-3)²+4
2
3
4
х
у=-2(х-3)²

18.

Построение графика функции
у= (х-3)³+2
у= (х-3)³+2
у
1). у=х³
2). у=х³-2 –сдвиг графика№1 вниз
вдоль оси Оу на 2 ед.
у=х³
3). у= (х-3)³ - сдвиг
графика№1 вправо вдоль
оси Ох на 3 ед.
у=х³-2
4). у= (х-3)³+2 – сдвиг
графика №3 вверх на 2
ед.
4
3
у=(х-3)³
2
1
0 1
2
3
4
х

19.

у
A(8;7)
у х 6 1
2
7
у х2 3
B(-4;3)
у х 8 7
2
D(6;1)
-8
-4
0 1
х
6
C(0;-3)
у= -2(х+4)²+3
у
-8
E(6;-8)
1
х 6 2 8
2

20.

Построение графика y=|f(x)|
у
у = |х²+6х+8|
-3
-2
у=х²+6х+8
у = |х²-6х+8|
-1
0
1
2
3
х
у=х²-6х+8
Части графика функции у=f(x), лежащие выше оси Ох и на оси Ох, остаются
без изменений, а лежащие ниже оси Ох -симметрично отражаются
относительно оси (вверх )

21.

Построение графика
y=f(|x|)
Часть графика функции у =f(x), лежащая левее оси Оу, удаляется , а часть,
лежащая правее оси Оу - остается без изменения и симметрично отражается
относительно оси Оу(влево). Точка графика, лежащая на оси Оу, остается
неизменной
у
8
7
6
у = х²-4|х|+2
у = х²-4х+2
5
4
3
2
1
-5
-4
-3
-2
-1
0 1
-1
-2
-3
х
2
3
4
5
6

22.

Построить график функции
6 , при х 3
х 3 , при 3 x 0
у
4 x 3 , при 0 x 2
5, при х 2
у
5
4
3
2
1
-6
-5 -4
-3
-2
-1
0 1
-3
-6
2
3
4
5
6
х

23.

Построить график функции
5 , при х 5
3 х 10 , при 5 x 2
у 2
x 2 x 4 , при - 2 x 3
2x - 7, при х 3
у
5
4
3
2
1
-7
-6
-5 -4
-3
-2
-1
0 1
-1
-2
-3
-4
-5
2
3
4
х

24.

1.Алгебра . 9 класс. Учебник для общеобразовательных организаций.
Под редакцией С.А. Теляковского .
Москва «Просвещение» 2013
2. Л.Э.Генденштейн, А.П. Ершова, А.С. Ершова
«Наглядный справочник по математике с примерами»
3. Фон презентации
http://7oom.ru/powerpoint/fon-dlya-prezentacii-bloknot-06.jpg