Похожие презентации:
Координаты вектора в пространстве. 12 кл
1. Векторы в пространстве
Координаты вектора12 класс
2.
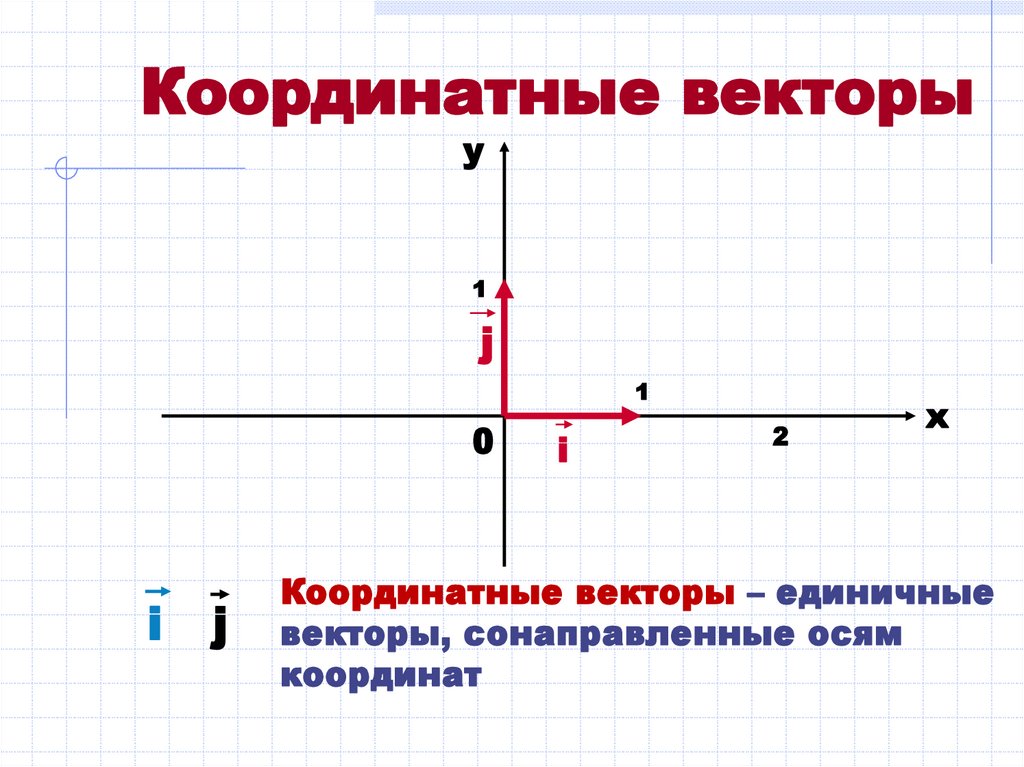
Координатные векторыy
1
j
1
0
i
j
i
2
x
Координатные векторы – единичные
векторы, сонаправленные осям
координат
3.
Координатные векторыi – единичный вектор оси абсцисс, j – единичный вектор
оси ординат, k – единичный вектор оси аппликат.
z
k
j
O
i
x
y
4. Координаты вектора
a=Xi+YjЧисла X и Y
называются
координатами вектора
a=(X;Y)
5.
y2
d
1
a
j
- 0,5
1
0
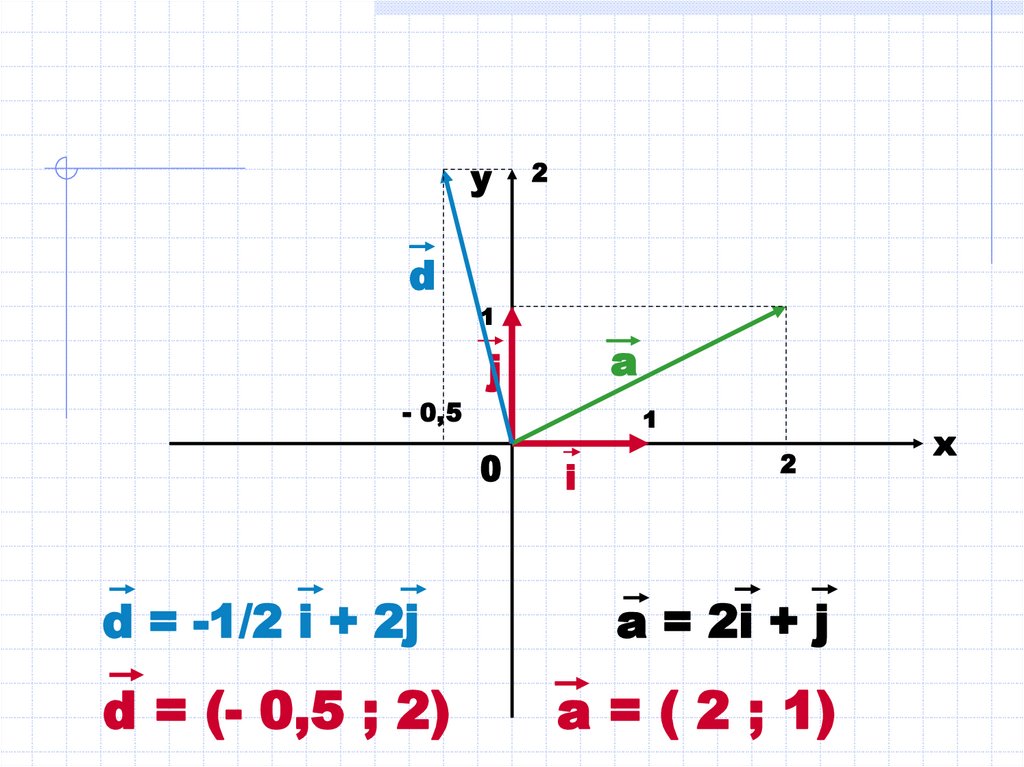
d = -1/2 i + 2j
d = (- 0,5 ; 2)
i
2
a = 2i + j
a = ( 2 ; 1)
x
6.
Координаты вектораЛюбой вектор в пространстве a можно разложить
по координатным векторам, т.е. представить в
виде суммы:
а X i Y j Zk
Нулевой вектор можно представить в виде:
0 0i 0 j 0k
7. Координаты вектора
a=Xi+Yj+ZkЧисла X, Y и Z
называются
координатами вектора
a = ( X ; Y; Z )
8. Длина вектора
|a| =X
2
Y
2
Длина вектора равна
корню квадратному из
суммы квадратов его
координат.
9. Длина вектора
|a| =X
2
Y
2
Z
Длина вектора равна
корню квадратному из
суммы квадратов его
координат.
2
10. Радиус - вектор
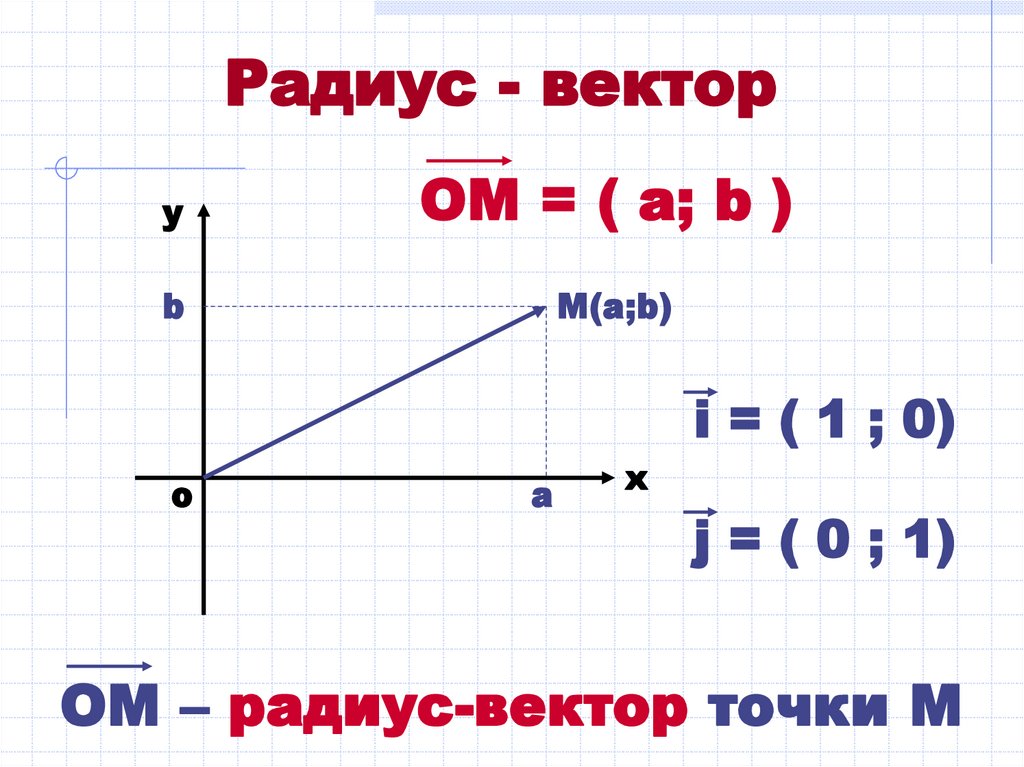
yOM = ( a; b )
b
M(a;b)
i = ( 1 ; 0)
o
a
x
j = ( 0 ; 1)
OM – радиус-вектор точки М
11.
Радиус - векторВектор, конец которого совпадает с данной точкой,
а начало – с началом координат, называется радиусвектором данной точки.
Координаты любой точки равны соответствующим
координатам её радус-вектора.
М (x; y; z)
OM =(x; y; z)
i = ( 1 ; 0 ; 0)
j = ( 0 ; 1 ; 0)
k = ( 0 ; 0 ; 1)
12. Равенство векторов
Векторы равны, еслиравны их
соответствующие
координаты.
u = (X1 ; Y1)
, v = (X2 ; Y2)
X1 = X2
Y1 = Y2
13. Равенство векторов
Векторы равны, еслиравны их соответствующие
координаты.
u = (X1 ; Y1 ; Z1 ) , v = (X2 ; Y2 ; Z2)
X1 = X2
Y1 = Y2
Z1 = Z2
14. Cумма векторов
Если a = (X1; Y1) иb = (X2; Y2) , то
a + b = (X1 + X2 ; Y1 + Y2)
Координаты суммы
векторов равны суммам
соответствующих
координат слагаемых.
15. Cумма векторов
Если a = (X1 ; Y1 ; Z1 ) иb = (X2 ; Y2 ; Z2), то
a + b = (X1 + X2 ; Y1 + Y2 ; Z1 + Z2)
Координаты суммы векторов
равны суммам
соответствующих координат
слагаемых.
16. Разность векторов
Если a = (X1; Y1) иb = (X2; Y2) , то
a - b = (X1 - X2 ; Y1 - Y2)
Координаты разности двух
векторов равны разностям
соответствующих координат
уменьшаемого и вычитаемого.
17. Разность векторов
Если a = (X1 ; Y1 ; Z1 ) иb = (X2 ; Y2 ; Z2), то
a - b = (X1 - X2 ; Y1 - Y2 ; Z1 - Z2)
Координаты разности двух
векторов равны разностям
соответствующих координат
уменьшаемого и вычитаемого.
18. Произведение вектора на число.
Если a = (X; Y), тоka = (kX; kY).
Чтобы умножить вектор
на число, нужно
умножить на это число
каждую из координат
вектора.
19. Произведение вектора на число.
Если a = (X ; Y ; Z ), тоka = (kX; kY; kZ).
Чтобы умножить вектор
на число, нужно
умножить на это число
каждую из координат
вектора.
20. Произведение вектора на число.
Если a = (X ; Y), то- a = (-X ; -Y).
Координаты
противоположного
вектора противоположны
координатам данного
вектора.
21. Произведение вектора на число.
Если a = (X ; Y ; Z ), то- a = (-X ; -Y ; -Z).
Координаты
противоположного
вектора противоположны
координатам данного
вектора.
22. Скалярное произведение векторов:
Если a = (X1; Y1) иb = (X2; Y2) , то
23. Скалярное произведение векторов:
Если a = (X1 ; Y1 ; Z1 ) иb = (X2 ; Y2 ; Z2), то




















 Математика
Математика








