Похожие презентации:
Матрицы. Определители и их свойства (лекция № 1)
1. лекция № 1 для студентов 1 курса обучающихся по специальности 030401 – Клиническая психология (очная форма обучения), к.п.н., доцент Шилина Ната
Кафедра медицинской и биологической физикиТема: Введение. Матрицы. Определители и их
свойства.
лекция № 1 для студентов 1 курса обучающихся по
специальности 030401 – Клиническая психология
(очная форма обучения),
к.п.н., доцент
Шилина Наталья Георгиевна
Красноярск, 2015
2. План лекции:
Введение.
Понятие матрицы.
Операции с матрицами.
Определители, их свойства.
Обратная матрица.
Характеристическое уравнение матриц.
3. Введение
• Широкоеиспользование
математических
методов в современном мире требует от
будущего психолога умения применять их при
работе с информацией и количественной
обработке
результатов
исследований.
Преподавание математики имеет большое
значение
в
формировании
научного
мировоззрения
и
развитии
научного
мышления студентов.
4. Введение
• В современной науке возникли новыенаправления,
такие,
например,
как
математическая
лингвистика,
математическая биология, математическая
экономика и т.п. Главная причина такого
явления заключается в том, что математика
предлагает общие, но вместе с тем очень
четкие логические модели для изучения
окружающей действительности на основе
своего особого языка – языка чисел и
символов.
5. Введение
• Объектами исследования математики служатлогические
модели,
построенные
для
описания
процессов,
происходящих
в
обществе,
природе,
технике,
живых
организмах. Математические модели дают
возможность прогнозировать явления с
количественной точки зрения, находить не
обнаруженные
ранее
закономерности,
определять условия, при которых возможно
решение теоретических и практических задач.
6. Введение
• Применение математических методоврасширяет
возможности
каждого
специалиста.
Существенную
роль
играет
раздел
математической
статистики, которая учит правильно
обрабатывать информацию, оценить
достоверность полученных данных,
сделать
прогноз
на
основании
имеющихся наблюдений.
7. Введение
• Любой психолог, как и математик,должен уметь рассуждать логически,
применять на практике дедуктивный и
индуктивный
методы.
Поэтому
математика
так
важна
для
специалистов-медиков.
Занимаясь
математикой,
будущий
специалист
формирует свое профессиональное
мышление.
8.
• Матрица это система элементов aijрасположенных в виде прямоугольной
таблицы. Элементы могут быть
числами, функциями или иными
величинами, над которыми можно
производить алгебраические операции
a11 ... a1n
A ... ... ...
am1 ... amn
9. Матрица
• Если матрица имеет m строк и n столбцов,то говорят о (m × n)-матрице.
m = 4; n =3 m × n = 12
10. Матрица
• Первый индекс элемента матрицы указываетномер строки, а второй – номер столбца
aij
11.
• Главной диагональю матрицы называетсядиагональ, идущая из левого верхнего угла
матрицы в правый нижний. При m=n
матрица называется квадратной, а число n
— её порядком. Квадратная матрица А
называется диагональной, если все ее
элементы, кроме находящихся на главной
диагонали, равны нулю.
1 0 0
А 0 2 0
003
12. Единичная матрица
– частный случай диагональной матрицы, вкоторой все элементы, находящиеся на
главной диагонали, равны 1.
1 0 0
01 0
0 0 1
13.
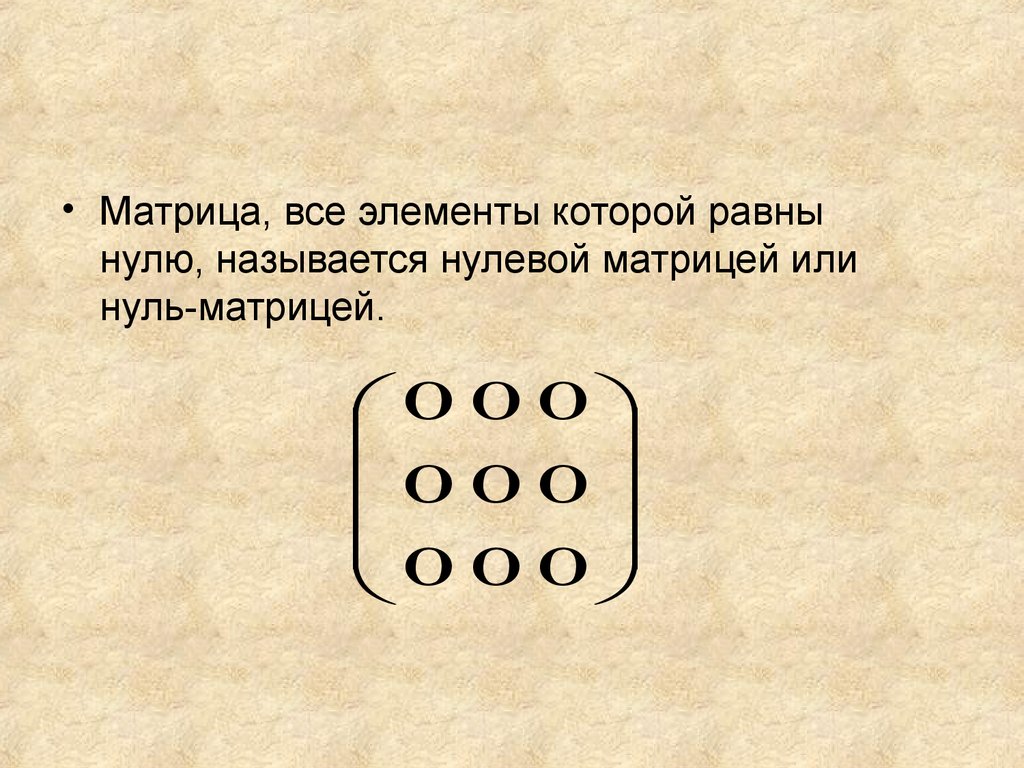
• Матрица, все элементы которой равнынулю, называется нулевой матрицей или
нуль-матрицей.
0 0 0
0 0 0
0 0 0
14.
• Матрица, состоящая из одной строки,называется строкой (строковой), из одного
столбца — столбцом.
• Если все ai = a, получают скалярную матрицу.
1 2 3 4
1
2
3
4
15.
Транспонирование матрицыПереставив в матрице строки со
столбцами,получают
транспонированную матрицу A’, или AT.
a11 ... a1n
a11 a12 ... a1n
T
A ... ... ... , то A ... ... ...
a a ... a
a
...
a
mn
1n 2 n
m1
mn
16. Транспонирование матрицы
Например:17.
• Наряду с конечными матрицами могутбыть матрицы с бесконечным числом
строк или столбцов
18. Действия над матрицами
• Умножениематрицы
на
число.
Произведением прямоугольной (m × n)матрицы А на число называют матрицу,
элементы
которой
получены
из
элементов aij умножением на число k:
ka11 ... ka1n
kA ... ... ...
ka ... ka
mn
m1
19. Например:
1 2 2 42
3 4 6 8
20.
Сложение матрицСумма прямоугольных матриц одинакового
размера равна:
a11 b11 ... an1 b1n
A B ...
...
...
a b ... a b
mn
mn
m1 m1
Например:
2
3
1 2 7 4
4 1 1 4
8
3
21.
• Умножениематриц
определяется
только для прямоугольных матриц
таких, что число столбцов первого
множителя равно числу строк второго.
Произведением (m × р) - матрицы А на
(р × n) - матрицу В будет (m × n)матрица С с элементами
• cij = ai1b1j + ai2b2j + ... + aipbpj,
• i =1, ..., m, j = 1, ..., n.
22. Найти произведение матриц:
1 21 2
1 1 2 5 1 2 2 3 11 8
и D CD
C
3 4
5 3
3 1 4 5 3 2 4 3 23 18
23.
Введённыедействия
над
матрицами
обладают свойствами, близкими к свойствам
действий
над
числами.
Исключением
является отсутствие коммутативного закона
при умножении матриц: равенство AB = BA
может не выполняться.
Матрицы А и В называются коммутирующими
(перестановочными), если AB = BA. Кроме
того, произведение двух матриц может
равняться нулевой матрице, хотя каждый
сомножитель отличен от нулевой.
24. Найти произведение матриц:
2 3А1
4 6
И
9 6
А2
6 4
2 9 ( 3) 6 ; 2 ( 6) ( 3) ( 4)
А1 А2
4 9 ( 6) 6; 4 ( 6) ( 6) ( 4)
0 0
0 0
9 2 ( 6) 4 ; 9 ( 3) ( 6) ( 6)
А2 А1
6 2 ( 4) 4; 6 ( 3) ( 4) ( 6)
6 9
4 6
А2 А1 А1 А2
25. Свойства действия умножения матриц
1.(AB)C = A(BC) - ассоциативностьумножения
2.(kA)B = A(kB) = k(AB)
3. ( A1 A2 ) B A1 B A2 B
4. A( B1 B2 ) AB1 AB2
26. Определители
• Пусть дана квадратная матрица второгопорядка
а11 а12
А
а21 а22
Определителем второго порядка,
соответствующим данной матрице,
называется число: a11a22 – a12a21.
27.
• Определитель обозначается символомdetA, Δ;
числа
a11,a12,a21a22
называются
элементами определителя;
• a11,a22 – образуют главную диагональ, а
a12,a21 – побочную. Следовательно чтобы
найти определитель второго порядка нужно
из произведения элементов главной
диагонали
вычесть
произведение
элементов второй диагонали.
Δ=
28. Свойства определителей
1. Определитель матрицы не меняется,если строки и столбцы меняются
местами (транспонирование)
2 2
2 3 2 1 6 2 4
1 3
2 1
2 3 2 1 6 2 4
2 3
29. Свойства определителей
2. Суммапроизведений
элементов
любой строки (любого столбца) на их
алгебраические дополнения равна
определителю матрицы.
3. Определитель равен 0, если все
элементы какой либо его строки
(столбца) равны 0
30. Свойства определителей
4. Если в определители поменятьместами две его любые строки (два
любых столбца), то определитель
изменит знак на противоположный.
5. Определитель,
содержащий
две
одинаковых строки (два одинаковых
столбца), равен нулю.
31. Свойства определителей
6. Общий множитель элементов любойстроки (столбца) можно выносить за
знак определителя.
7. Определитель не изменится, если к
элементам
какой-нибудь
строки
(столбца) прибавить соответствующие
элементы другой строки (столбца),
умноженные на произвольное число.
32. Минор
• Минор Мij элемента аij - определительполученный в результате вычеркивания
i–й строки и j- го столбца матрицы
• Матрица миноров имеет такой размер,
как и матрица А
• Например:
3 2 1
2 0 3
4 2 1
2 3
М 12
2 1 4 3 2 12 10
41
33. Пример
Дана матрицаМатрица миноров имеет вид
Находим минор для первого элемента.
Оставшееся число и является минором
данного элемента, которое записываем в нашу матрицу миноров.
По аналогии находим другие миноры
34. Алгебраическое дополнение
• Минор Мij умноженный на 1 i j называетсяалгебраическим дополнением Аij элемента аij
Aij ( 1)
i j
M ij
35. Для рассмотренного примера
3 2 12 0 3
4 2 1
М 12 10
М 12
2 3
4 1
2 1 4 3 2 12 10
1 2
А12 ( 1) ( 10) 10
Для второй матрицы необходимо поменять знаки у выделенных членов
36.
• Определителемтретьего
порядка,
соответствующим данной квадратной матрице
третьего
порядка,
называется
число,
обозначаемое
и
получаемое
следующим
образом:
• Таким образом, эта формула даёт разложение
определителя третьего порядка по элементам
первой строки a11, a12, a13 и сводит вычисление
определителя третьего порядка к вычислению
определителей второго порядка.
37. Обратная матрица
• Понятие обратной матрицы вводится толькодля квадратных матриц.
• Если A – квадратная матрица, то обратной
для неё матрицей называется матрица,
обозначаемая
A-1
и
удовлетворяющая
условию
Теорема. Для того чтобы квадратная матрица A
имела обратную, необходимо и достаточно,
чтобы её определитель был отличен от нуля.
38.
Итак, чтобы найти обратную матрицу нужно:Найти определитель матрицы ІAІ.
Найти алгебраические дополнения Aij всех
элементов матрицы A и составить
матрицу A′ , элементами которой являются
числа Aij.
Найти матрицу, транспонированную
полученной матрице AT, и умножить её на
1
A
39. Пример: найти обратную матрицу
1 2А
3 4
Находим определитель матрицы: ІАІ =1·4 – 2·3 = – 2
4 3
Находим матрицу миноров: М
2 1
4 3
Алгебраическое дополнение (меняем знак у 2-х членов): А*
2 1
4 2
Т
Транспонируем матрицу дополнений: А*
3 1
1 Т
1 4 2
А*
Обратная матрица: А
А
2 3 1
1
40. Тест
Порядок прямоугольной матрицы,имеющей m строк и n столбцов равен
1. (m x n)
2. (m+n)
3. (m)
4. (n)
41. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА:
Основная литература:• Ганичева А.В., Козлов В.П. Математика
для психологов. М.: Аспект-пресс, 2005,
с.81-89.
• Павлушков И.В. Основы высшей
математики и математической статистики.
М., ГЭОТАР-Медиа, 2007.
• Журбенко Л. Математика в примерах и
задачах. М.: Инфра-М, 2009.

















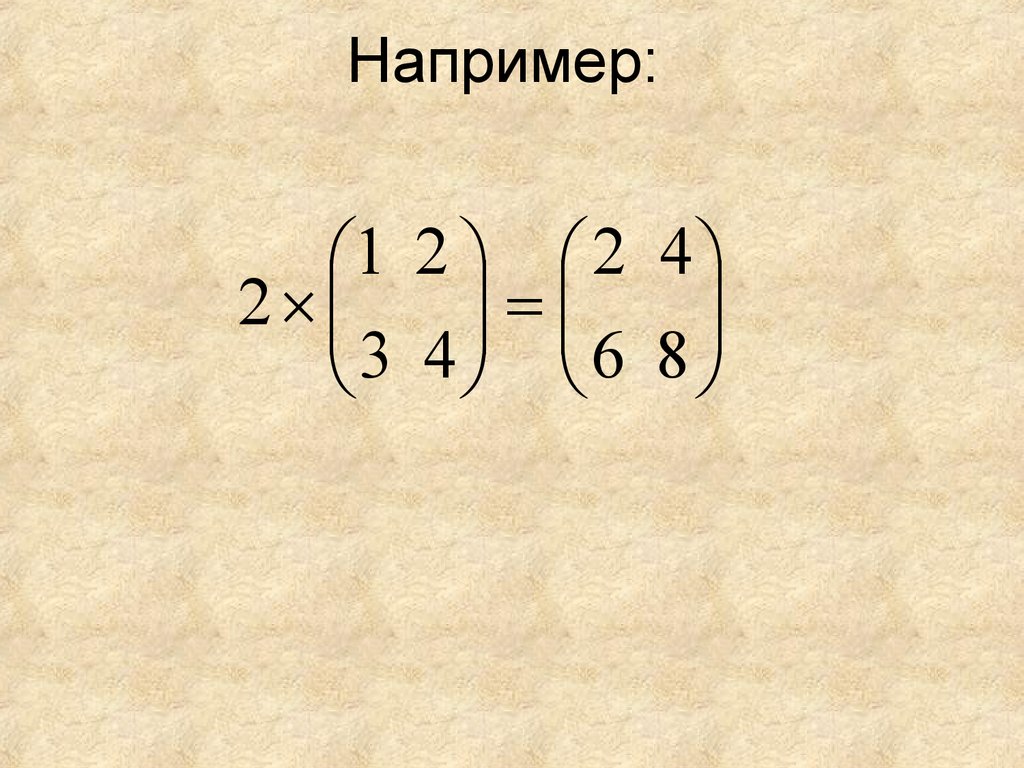














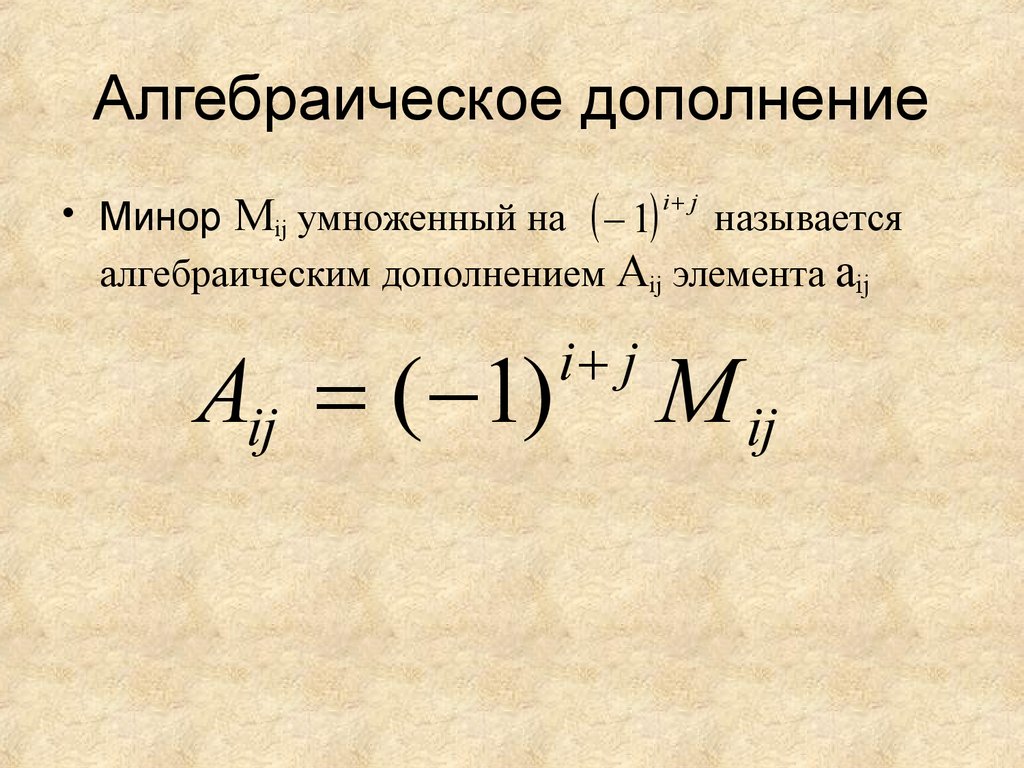








 Математика
Математика








