Сечения параллелепипеда

1.

2. Параллелепипед

D1
C1
B1
A1
D
A
C
B

3. В строительстве и архитектуре

4. Построение сечений в параллелепипеде:

По трем точкам, лежащим на трех
соседних ребрах.
По трем точкам, лежащим на трех
параллельных ребрах (Случай 1).
По трем точкам, лежащим на трех
параллельных ребрах (Случай 2).
По трем точкам, не лежащим на трех
параллельных ребрах (Случай 1).
По трем точкам, не лежащим на трех
параллельных ребрах (Случай 2).

5.

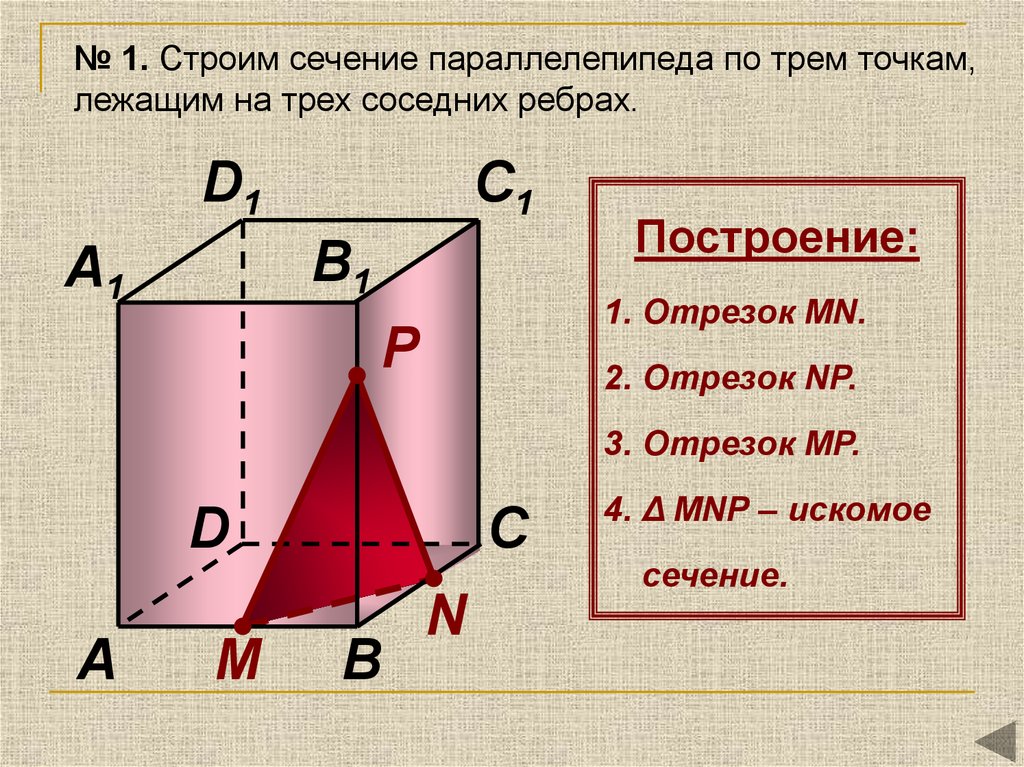
№ 1. Строим сечение параллелепипеда по трем точкам,
лежащим на трех соседних ребрах.
D1
C1
B1
A1
Построение:
1. Отрезок MN.
P
2. Отрезок NР.
3. Отрезок MР.
D
A
М
C
B
N
4. Δ MNР – искомое
сечение.

6.

№ 2. Строим сечение параллелепипеда по трем точкам,
лежащим на трех параллельных ребрах (Случай 1).
D1
Q
A1
C1
1. Отрезок MN.
B1
2. Отрезок NР.
P
3. РQ II MN.
4. PQ ∩ DD1 = Q.
М
D
A
Построение:
5. MQ II NP.
N
B
C
6. MNРQ –
искомое сечение.

7.

№ 2. Строим сечение параллелепипеда по трем точкам,
лежащим на трех параллельных ребрах (Случай 2).
R
D1 Q
A1
М
C1
B1
Построение:
1. Отрезок MN.
2. Отрезок NР.
P
3. РQ II MN,
PQ ∩ C1D1 = Q.
4. MR II NP,
D
A
N
B
C
MR ∩ A1D1 = R.
5. Отрезок QR.
6. MNРQR – искомое
сечение.

8.

№ 3. Строим сечение параллелепипеда по трем точкам,
не лежащим на трех параллельных ребрах (Случай 1).
D1
P C1
Построение:
1. Отрезок MN.
A1
B1
Q
2. Отрезок NР.
3. РQ II MN.
4. PQ ∩ А1В1 = Q.
5. Отрезок MQ.
D
A
C
М
B
N
6. MNРQ –
искомое сечение.

9.

Строим сечение
параллелепипеда
по трем точкам, не
лежащим
на трех
параллельных
ребрах
(Случай 2).
№ 3.
E
Q
D1 P
A1
C1
B1
N
R
К
C
D
L
A
S
B
М

10.

№ 3.
Построение:
E
Q
1. Отрезок MN.
D1 P
A1
C1
3. NP ∩ CD = K.
B1
4. MK ∩ AB = S.
5. MS ∩ AD = L.
6. PN ∩ DD1 = E.
N
R
D
L
2. Прямая NР.
A
C
S B
М
К
7. Прямая LE.
8. LE ∩ AA1 = R.
9. LE ∩ A1D1 = Q.
10.MNРQRS –
искомое сечение.

11. Верно ли построено сечение через точки M, N и P?

D1
A1
C1
P
B1
N
D
A
P
М
М
C1
B1
C
B
Q
D
A
C
N