Похожие презентации:
Теория кривых. Соприкасающаяся окружность плоской кривой
1. ТЕОРИЯ КРИВЫХ
Соприкасающаясяокружность плоской
кривой
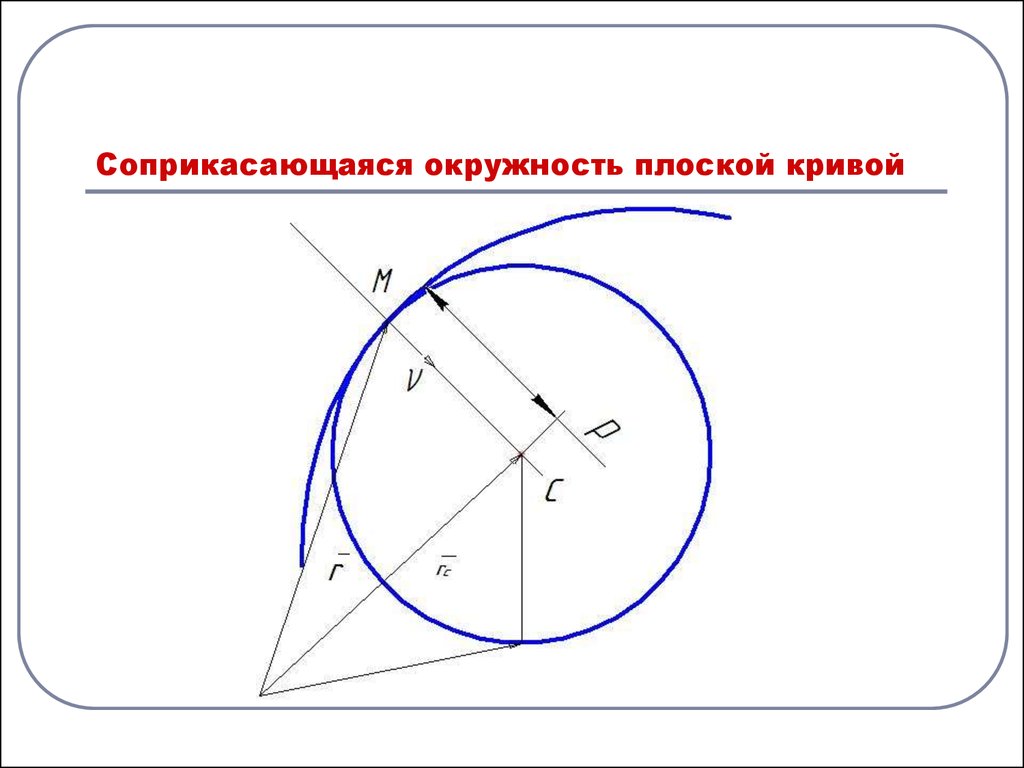
2. Соприкасающаяся окружность плоской кривой
Определение: Окружность, проходящая через три точки плоскойкривой, бесконечно сближающихся к данной точке
кривой, называется соприкасающейся
окружностью.
Рассмотрим плоскую кривую, -вектор главной нормали плоской
кривой. Относительно точки М вдоль отложим расстояние
1
p , где k – кривизна плоской кривой в точке М, получим точку С.
k
Строим окружность с центром в точке С и радиусом р. Это и есть
соприкасающаяся окружность плоской кривой, построенная в
точке М. р – радиус кривизны кривой, а С – центр кривизны кривой.
3. Соприкасающаяся окружность плоской кривой
4. Уравнение соприкасающейся окружности
Пусть кривая задана: r r (s )rC rM p
1
rC rM p rM 2 r
k
r
rM r (s)
k
p
1
,
k
( xC ) 2 ( yC ) 2 p 2
( rC ) 2 p 2
( r ( s)
1
1
2
r
(
s
))
2
k2
k
(42) – уравнение соприкасающейся окружности.
(42)



 Математика
Математика








