Формулы вычисления кривизны и кручения кривой в случае натуральной параметризации

Формулы для вычисления кривизны и кручения кривой в случае произвольной параметризации

168.50K

Категория: $Математика$ Математика

Похожие презентации:

Теория кривых. Репер Френе

Теория кривых. Сопровождающий трехранник

Теория кривых. Кривизна плоской кривой

Теория кривых. Плоские кривые

Теория кривых. Эволюта и Эвольвента

Кривые на плоскости

Теория кривых. Формулы Сере-Френе

Инженерные кривые и поверхности

Теория поверхностей. Нормальная кривизна линии на поверхности. Вторая квадратичная форма поверхности.

Разбивка кривой

Теория кривых. Кривизна и кручение кривой

1. ТЕОРИЯ КРИВЫХ

Кривизна и кручение
кривой

2. Кривизна

Определение: предел отношения угла поворота касательной на
дуге кривой, стягивающейся к данной точке, к
длине этой дуги называется кривизной кривой в
данной точке.
lim
s 0
S
(*) – кривизна кривой.
(*)

3. Кривизна

Утверждение (о кривизне):
Величина k в формулах Серре-Френе равна кривизне кривой.
Лемма:
Отношение модуля приращения единичного переменного вектора
к углу его поворота при стремлении этого угла к нулю равен
единице.
Доказательство леммы:
| m | 1
A2
A1
| m |
Δm
lim
1
φ
0
m
m
| m |
lim 1
(*)
0
A1 A2
(хорда в пределе равна длине дуги окружности).

4. Кривизна

5. Кривизна

По лемме:
Ч.т.д.
lim
0
| |
1 k lim
S 0
S

6. Кручение

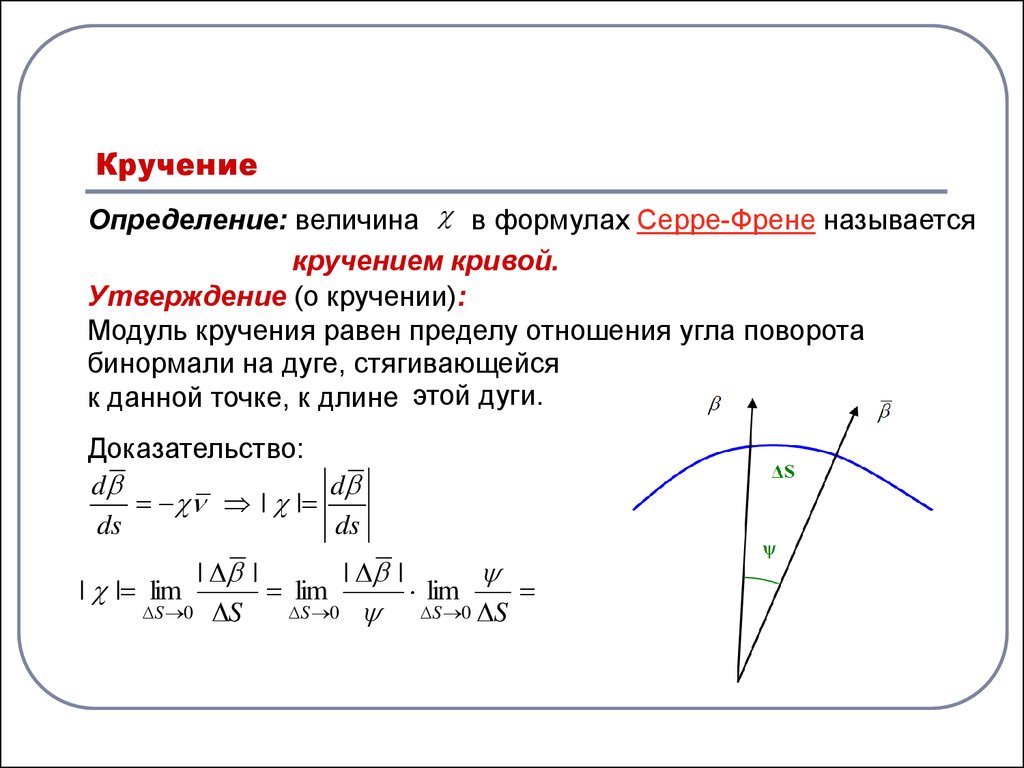
Определение: величина в формулах Серре-Френе называется
кручением кривой.
Утверждение (о кручении):
Модуль кручения равен пределу отношения угла поворота
бинормали на дуге, стягивающейся
к данной точке, к длине этой дуги.
Доказательство:
d
d
| |
ds
ds
| |
| |
lim
lim
S 0 S
S 0
S 0 S
| | lim

7. Кручение

lim
| |
0
Ч.т.д.
lim
S 0
S
(по Лемме) lim
S 0
S

8. Формулы вычисления кривизны и кручения кривой в случае натуральной параметризации

Кривая задана: r r (s )
r
| r | k .
| [r ; r ] | | | | r | sin 90 | r | k
k | [r ; r ] |
(24)
(24) – формулы кривизны в натуральной параметризации.
r k ,
( 23)
r (k ) k k k k ( k ) k k 2 k
Рассмотрим смешанное произведение векторов r , r , r .
r r r k (k k 2 k ) k k =(свойства Репера Френе)=
k 2
k 2
1

9. Формулы вычисления кривизны и кручения кривой в случае натуральной параметризации

r r r
k2
Воспользуемся формулой (24) и получим:
r r r
[r ; r ] 2
(25)
(25) – формулы вычисления кручения кривой в натуральной
параметризации

10. Формулы для вычисления кривизны и кручения кривой в случае произвольной параметризации

Кривая задана: r r (t )
d
Введём обозначения:
ds
d
" "
dt
" '"
t'
d
dt d
dt ds dt
d
d
s
dt
ds
r r t
r r s
s 0 s | r | , так как | r | 1.
r
1
1
r
r t
t
| r |
s | r |
r r t r t r t 2 r t
Подставим найденные вектора в формулу (24):

11. Формулы для вычисления кривизны и кручения кривой в случае произвольной параметризации

k | [r ; r ] | | [r t ; r t 2 r t ] | t 3 | [r ; r ] |
и окончательно получим:
| [r ; r ] |
k
| r 3 |
(26)
(26) - формула вычисления кривизны кривой в случае
произвольной параметризации.
r ( r t 2 r t ) ( r t 2 ) (r t ) r t 2 2t t r r t r t r t 3 3t t r r t
Рассмотри смешанное произведение векторов r , r , r
(r r r ) r t ( r t 2 r t ) ( r t 3 3t t r r t ) t 6 (r r r )
И векторное произведение векторов
[r ; r ] t 3 [r ; r ]
r , r

12. Формулы для вычисления кривизны и кручения кривой в случае произвольной параметризации

Найденные нами произведения подставим в формулу (25)
r r r t 6 (r r r )
6
2
[r ; r ]
t [r ; r ] 2
r r r
[r ; r ]2
(27)
(27) – формулы вычисления кручения кривой в случае
произвольной параметризации
Утверждение 4.
Кривая лежит в одной плоскости 0
этой кривой.
в каждой точке

13. Точки спрямления и уплощения

Доказательство:
Пусть кривая лежит в одной плоскости, следовательно,
r , r , r лежат в этой плоскости r r r 0
( 25)
0
утв 3
Пусть 0 r r r 0 r , r , r лежат в одной
плоскости r лежит в одной плоскости в любой точке
Кривой, следовательно, кривая плоская.
Ч.т.д.
Определение: точка пространственной кривой называется
точкой спрямления, если в этой точке k=0.
Определение: точка пространственной кривой называется
точкой уплощения, если в ней 0.
Выход