Теория поверхностей.Нормальные сечения поверхности. Теорема Менье

1. ТЕОРИЯ ПОВЕРХНОСТЕЙ

Определение нормального
сечения. Свойство
нормального сечения.
Теорема Менье. Индикатриса
Дюпена

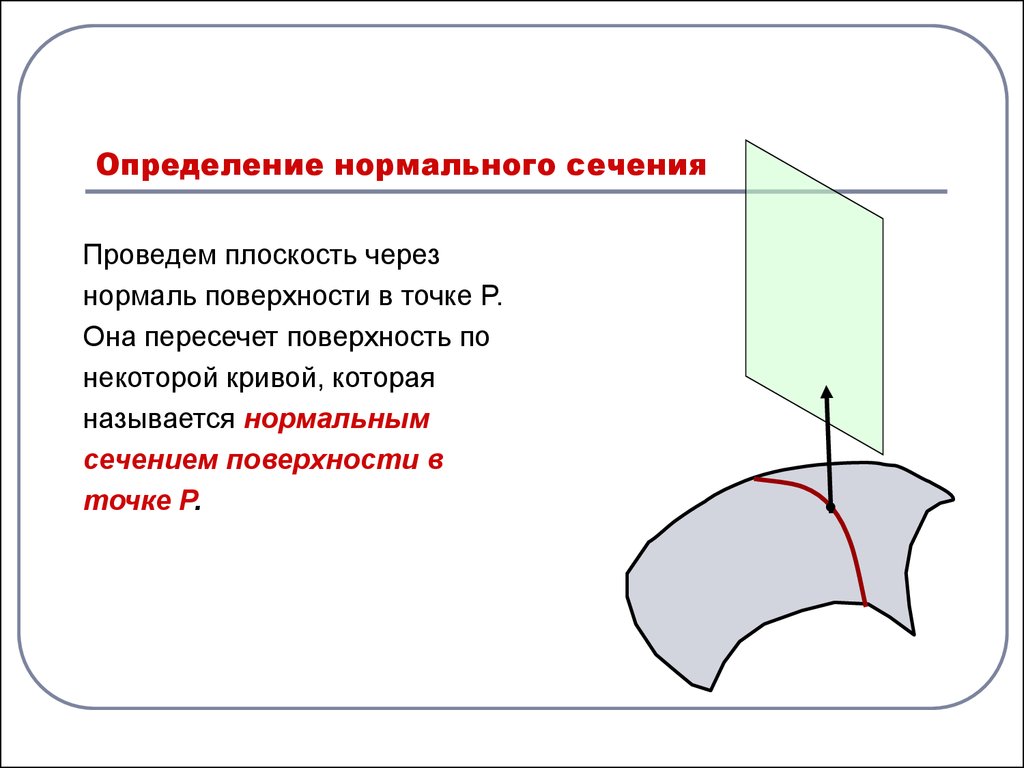
2. Определение нормального сечения

Проведем плоскость через
нормаль поверхности в точке P.
Она пересечет поверхность по
некоторой кривой, которая
называется нормальным
сечением поверхности в
точке P.

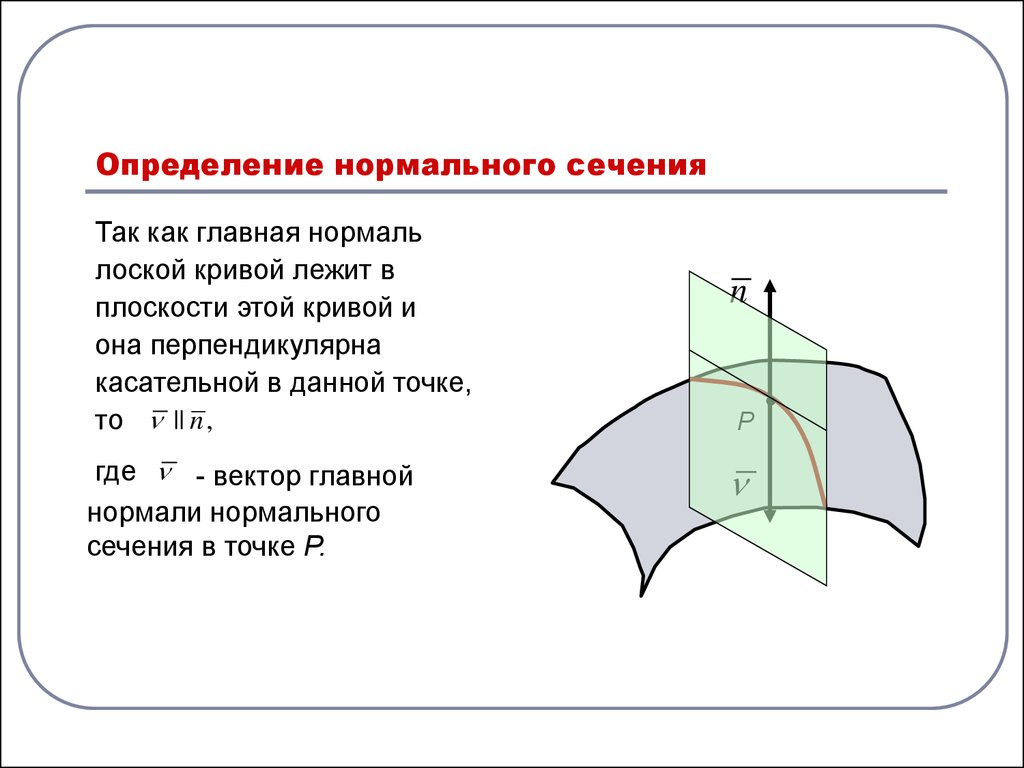
3. Определение нормального сечения

Так как главная нормаль
лоской кривой лежит в
плоскости этой кривой и
она перпендикулярна
касательной в данной точке,
то || n ,
где - вектор главной
нормали нормального
сечения в точке P.
n
P

4. Определение нормального сечения

Нормальное сечение называется вогнутым, если n
и выпуклым, если n .
n
n
P
P
Вогнутое сечение
Выпуклое сечение

5. Свойство нормального сечения

Утверждение 3
Нормальная кривизна kn поверхности в точке P в направлении
нормального сечения равна кривизне нормального сечения k
n 1
в этой точке, взятой со знаком +, если сечение вогнутое, и со
знаком –, если сечение выпуклое: k n k
Доказательство:
kn прn r прn ( k ) k( n ) k
«+» - для вогнутых сечений, т.к. для них n , и поэтому
«-» - для выпуклых сечений, т.к. в этом случае n 1
Ч.т.д.

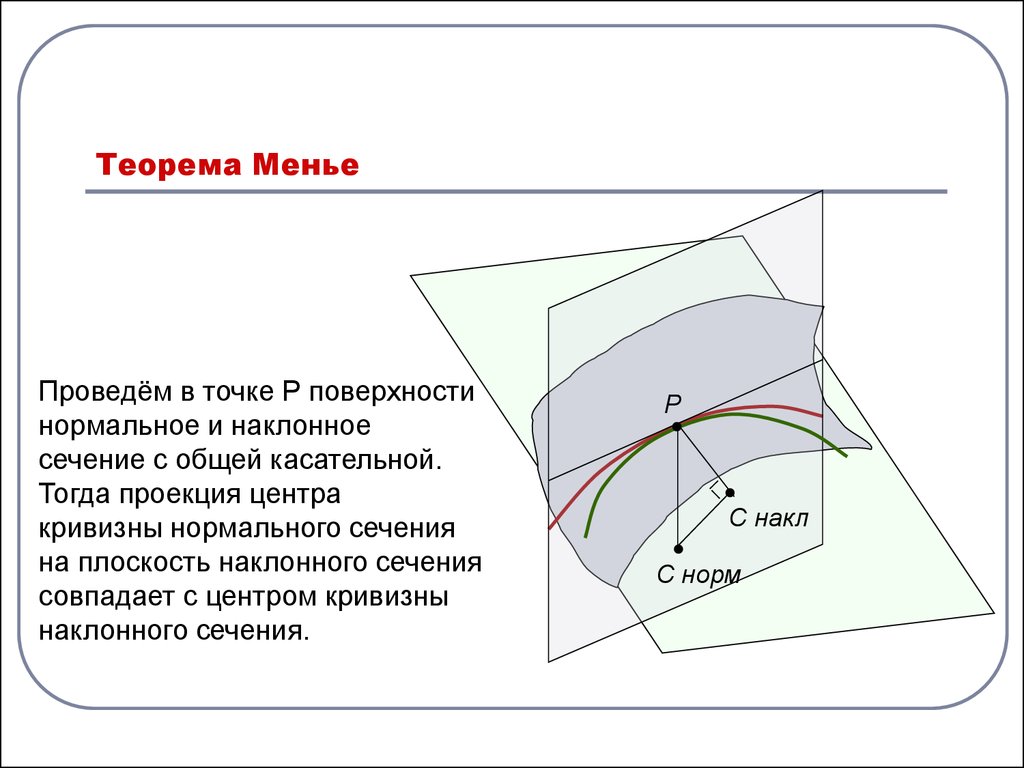
6. Теорема Менье

Проведём в точке Р поверхности
нормальное и наклонное
сечение с общей касательной.
Тогда проекция центра
кривизны нормального сечения
на плоскость наклонного сечения
совпадает с центром кривизны
наклонного сечения.
P
C накл
C норм

7. Теорема Менье

В силу утверждения 2: knнорм knнакл
(*)
knнорм kнорм
(**)
n kнакл наклn
k nнакл rнакл
Θ – угол между плоскостями нормального и наклонного сечения
(острый).
наклn cos
“+”, если n норм , для вогнутых нормальных сечений;
“-“, если n норм , для выпуклых нормальных сечений.
knнакл kнакл ( cos ) подставим эту формулу и (**) в (*):
kнорм kнакл cos , следовательно,
k норм k накл cos

8. Теорема Менье

kнорм
1
рнорм
,
р накл р норм cos
Ч.т.д.
k накл
1
рнакл
,
следовательно,

9. Определение индикатрисы Дюпена

Определение: проведём в точке Р поверхности касательную
плоскость и в ней отложим от этой точки отрезок
1
, где k n - нормальная кривизна
длины
| kn |
поверхности в точке Р в направлении, в котором
откладывается отрезок в касательной плоскости.
Противоположный конец отрезка опишет кривую в
касательной плоскости, которая называется
индикатрисой Дюпена.

10. Определение индикатрисы Дюпена

11. Уравнение индикатрисы Дюпена

Зададим в касательной плоскости систему координат Pxy, с базисом
y dv
ru , rv , т.е.
(*)
x du
Пусть точка М(x,y) на индикатрисе Дюпена, тогда
1
1
PM xru yrv . Так как | PM |
, то
( xru yrv ) 2 ,
| kn |
| kn |
1
,а
следовательно, Ex 2 2 Fxy Gy 2
kn
Edu 2 2 Fdudv Gdv 2
2
2
Ex
2
Fxy
Gy
| Ldu 2 2Mdudv Ndv 2 |
Ldu 2 2Mdudv Ndv 2
kn
Edu 2 2 Fdudv Gdv 2

12. Уравнение индикатрисы Дюпена

y2
Умножим числитель и знаменатель левой дроби на
,
2
dv
Получим с использованием равенства (*):
Ex 2 2 Fxy Gy 2
Ex 2 2 Fxy Gy 2
2
2
| Lx 2Mxy Ny |
или Lx 2 2Mxy Ny 2 1
| Lx 2 2Mxy Ny 2 | 1
(23)
(23) – уравнение индикатрисы Дюпена в системе координат Pxy
в касательной плоскости.

13. Виды индикатрис Дюпена. Типы точек на поверхности

Lx 2 2Mxy Ny 2 1
Индикатриса Дюпена – кривая второго порядка, в уравнении
которой отсутствует слагаемые первой степени. Следовательно
ИД не может быть параболой y2=2px
Вид кривой зависит от значения инварианта I2
I2
L
M
M
N
LN M 2
2
1. Если I 2 0 ( LN M 0), следовательно, индикатриса
Дюпена – эллипс, и точка Р на поверхности называется
эллиптической.

14. Виды индикатрис Дюпена. Типы точек на поверхности

2
2. Если I 2 0 ( LN M 0), следовательно, индикатриса Дюпена
– пара смежных гипербол, точка Р называется
гиперболической.
2
3. Если I 2 0 ( LN M 0), тогда индикатриса Дюпена – пара
параллельных прямых, точка Р называется параболической.

15. Пример

1. На эллипсоиде все точки эллиптические.
2. На однополостном гиперболоиде и гиперболическом
параболоиде все точки гиперболические.
3. На торе все три типа точек на поверхности присутствуют:
Во внешней части тора – эллиптические
точки, во внутренней части гиперболические точки, а на окружностях,
разделяющих внешнюю и внутреннюю
части – параболические точки.
Вблизи эллиптической точки поверхность
представляет собой часть эллипсоида.
В близи гиперболической точки
поверхность представляет собой
гиперболический параболоид, а вблизи
параболической точки – цилиндр.