Теория поверхностей. Задание поверхности

1. ТЕОРИЯ ПОВЕРХНОСТЕЙ

Задание поверхности

2. Определение поверхности

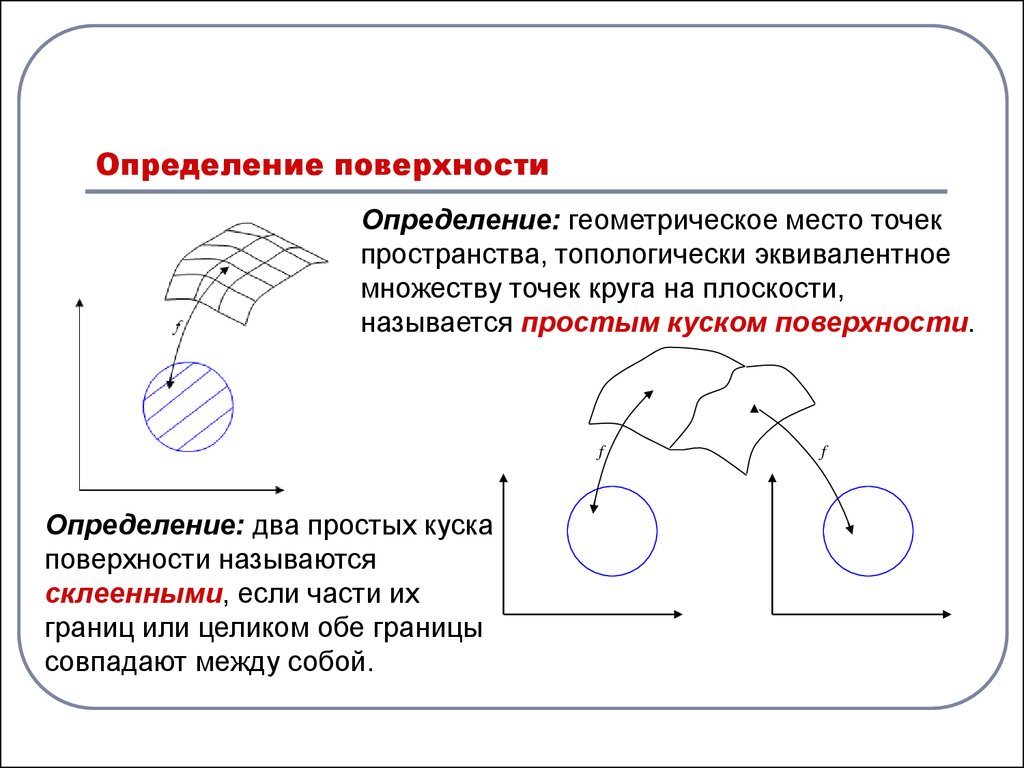
Определение: геометрическое место точек
пространства, топологически эквивалентное
множеству точек круга на плоскости,
называется простым куском поверхности.
f
Определение: два простых куска
поверхности называются
склеенными, если части их
границ или целиком обе границы
совпадают между собой.
f

3. Определение поверхности

Определение: поверхностью называется множество точек,
которые могут быть склеены из конечного или
счётного множества простых кусков.

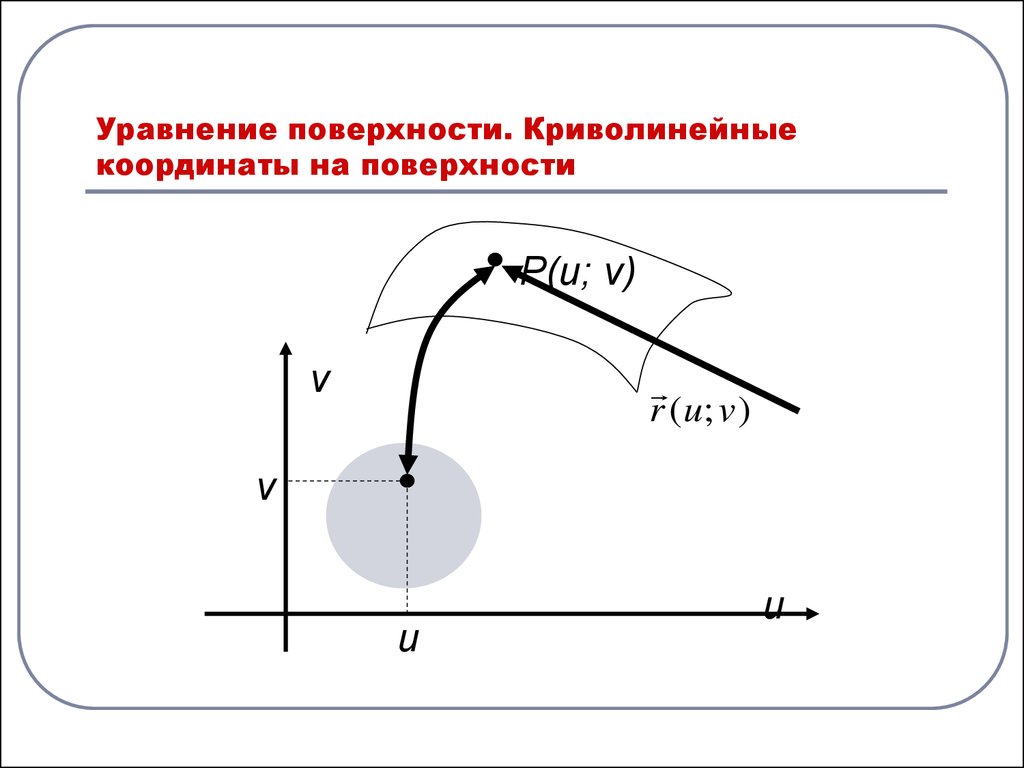
4. Уравнение поверхности. Криволинейные координаты на поверхности

P(u; v)
v
r ( u; v )
v
u
u

5. Уравнение поверхности. Криволинейные координаты на поверхности

r r (u, v)
(1)
(1) - выражает радиус-вектор точек поверхности в некоторой
системе координат как функцию двух параметров u и v.
x x(u , v)
y y (u , v)
z z (u , v)
(2) - параметрическое уравнение поверхности.
В отличие от кривых, поверхности параметризуются двумя
параметрами u и v.
(2)

6. Уравнение поверхности. Криволинейные координаты на поверхности

x
u
I
x
v
y z
u u
y z
v v
(5) – матрица Якоби.
x y
Пусть ux uy 0,из теоремы об обратной функции следует,
v v
что первые два уравнения системы (2) можно обратить:
u u ( x, y )
v v( x, y )
z z (u , v)
(5)

7. Уравнение поверхности. Криволинейные координаты на поверхности

z f ( x, y )
(3)
(3) – задание поверхности в явном виде.
F ( x, y , z ) 0
(4)
(4) – неявное уравнение поверхности.
Определение: рассмотрим линии на поверхности, в каждой точке
которой выполняется: u u 0 - const или v v0 - const
Такие линии на поверхности называются
координатными, а u, v - криволинейными
координатами.
Определение: если в каждой точке поверхности ранг матрицы
Якоби (3) равен 2, то система криволинейных
координат на поверхности называется правильной.

8. Уравнение поверхности. Криволинейные координаты на поверхности

Рассмотрим линию
v v0 - const
r r (u, v0 ) - уравнение кривой.
r
ru
- касательный вектор к линии
u
v const.
Рассмотрим линию
u u 0 - const
r r (u 0 , v) - уравнение кривой.
r
rv
- касательный вектор к линии
v
u const .

9. Уравнение поверхности. Криволинейные координаты на поверхности

Определение: ru , rv - называются координатными векторами.
ru {xu , yu , zu }
- строки в матрице Якоби.
rv {xv , y v , z v }
Утверждение:
Сеть криволинейных координат – правильная ru не
коллинеарен
rv .