Вычисление интегралов вида R(x, Jax2 + bx+c) dx

1. Здравствуйте!

Лекция №6

2.

Вычисление интегралов вида R x, ax2 bx c dx .
Подстановки Эйлера
Первая подстановка Эйлера
Эту подстановку можно применять, если выполнено условие
a 0 . Она имеет вид
t ax2 bx c a x .
Проделаем все вычисления, взяв, для определенности, знак +.
Тогда
ax2 bx c t x a .
Возводим это выражение в квадрат
ax2 bx c t 2 2tx a ax2 ,
сокращаем ax 2 и выражаем в явном виде х через t:
t2 c
.
x
b 2 at

3.

Теперь можно выразить через t и комбинацию ax2 bx c .
Имеем
t2 c
2
,
ax bx c t x a t a
b 2 at
и корень исчезает. Далее,
at 2 bt c a
dx 2
dt
2
(2 at b)
и подстановка всего этого в исходный интеграл приводит его к виду
t2 c
t2 c
at 2 bt c a
R b 2 at , t a b 2 at 2 (2 at b)2 dt
и под знаком интеграла стоит дробно рациональная функция от
переменной t.

4.

Вторая подстановка Эйлера
Эту подстановку можно применять, если выполнено условие
c 0 . Она имеет вид
ax2 bx c xt c .
Возведем в квадрат и приравняем обе части равенства:
ax 2 bx c x 2t 2 2 xt c c.
Вычеркнем c в правой и левой части равенства. Разделив затем обе
части полученного равенства на x, получим:
ax b xt 2 2t c.

5.

Откуда выражаем x через t:
x
2 ct b
2
R
(
t
),
ax
bx c xt c R2 (t ),
1
2
a t
2 c (a t 2 ) 2t ( 2 ct b)
dx
dt R3 (t )dt.
2 2
(a t )
Окончательно получаем:
2
R
(
x
,
ax
bx c )dx R( R1 (t ), R2 (t )) R (t )dt,
3
где R1 , R2 , R3 - рациональные функции. Таким образом, пришли к
интегралу от рациональной функции. После вычисления этого
ax 2 bx c c
интеграла нужно положить t
.
x
Следует отметить, однако, что вторая подстановка Эйлера
обычно приводит к громоздким вычислениям и поэтому ее
применяют редко.

6.

Третья подстановка Эйлера.
Условие применимости этой подстановки: полином ax 2 bx c
имеет действительные корни х1 и х2.
Сама третья подстановка Эйлера имеет вид
ax 2 bx c
t
.
x x1
Покажем, что она сводит наш интеграл к интегралу от дробно
рациональной функции. Так как ax 2 bx c a( x x1 )( x x2 ) , то
2
ax
bx c a ( x x1 )( x x2 )
x x2
t2
a
.
2
2
( x x1 )
( x x1 )
x x1
Отсюда находится х через t:
t 2 x1 ax2
x 2
.
t a

7.

ax2 bx c получаем
t 2 x1 ax2
t
2
,
ax bx c t ( x x1 ) t 2
x1 a( x1 x2 ) 2
t a
t a
и корень исчезает. Легко получить, что
2a( x2 x1 )t
dx
dt
2
2
(t a)
и рассматриваемый интеграл приводится к виду
t 2 x1 ax2 a( x1 x2 )t 2a( x2 x1 )tdt
R t 2 a , t 2 a (t 2 a)2 ,
и под знаком интеграла снова получилась дробно рациональная
функция от переменной t.
Для комбинации

8.

2
ax + bx + c
a>0
x
Применима первая подстановка Эйлера

9.

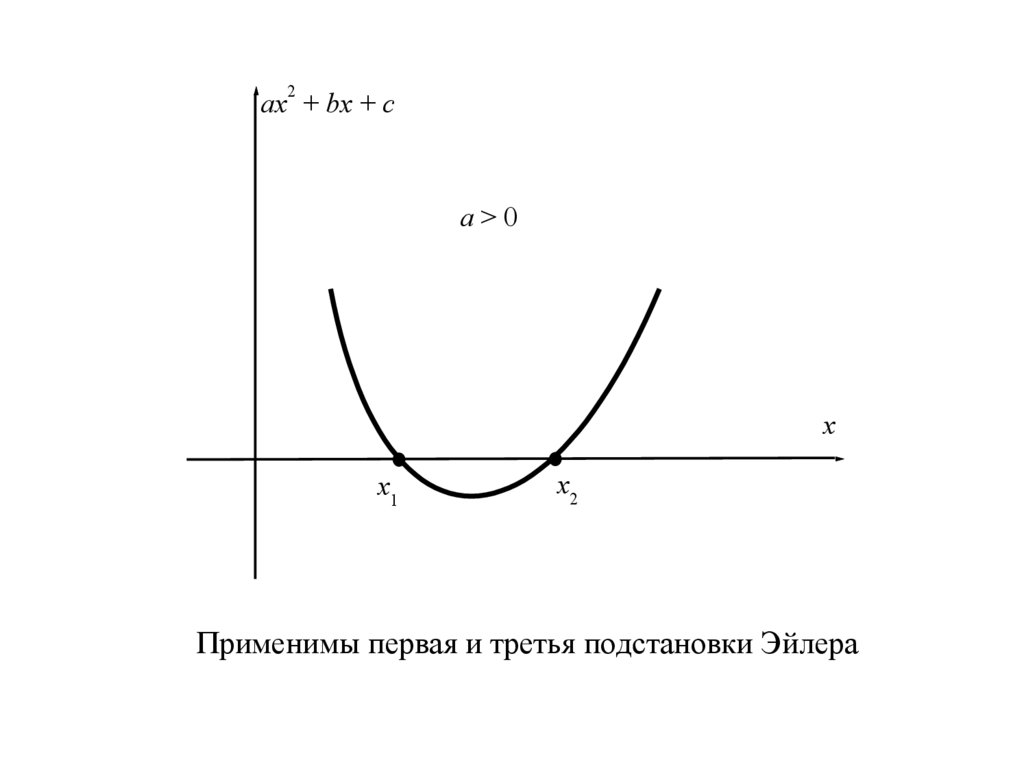
2
ax + bx + c
a>0
x
x1
x2
Применимы первая и третья подстановки Эйлера

10.

2
ax + bx + c
x1
x2
x
a<0
Применима третья подстановка Эйлера

11.

2
ax + bx + c
x
a<0
Подкоренное выражение всегда отрицательно, поэтому интеграл не
имеет смысла.

12. Конец первой части

13. Часть 2

Определённый интеграл

14.

Процедура построения определенного интеграла
Пусть нам заданы следующие объекты
1. Отрезок [a, b] конечной длины b a .
2. Функция f (x) , которая определена и ограничена на этом
отрезке.
Проведем следующее построение:

15.

1. Разбиение отрезка на кусочки
Разобьем отрезок [a, b] произвольным образом на части
(кусочки) точками a x0 x1 x2 x3 ... xn 1 xn b (см. рис.).
Для единообразия, точку а будем называть точкой х0, а точку b
точкой хп.
0
x
a = x0
1
x
x1
2
x
x2
x3
...
xn-1
n-1
x
b = xn
Пусть xi xi 1 xi есть длина i-го кусочка и max xi самая
i
большая из этих длин.

16.

2. Составление интегральной суммы
На каждом из кусочков [ xi , xi 1 ] возьмем произвольно
некоторую точку i (она называется средней точкой, хотя,
конечно, не обязательно лежит на середине кусочка), так что
[ xi i xi 1 ] и составим сумму
n 1
f ( i ) xi ,
i 0
которая называется интегральной суммой.

17.

f (x)
f ( 2)
f ( 1)
f ( 0)
x
a = x0
0
x1
1
x2 2
b = x3
Геометрически она представляет собой сумму площадей
прямоугольников высотой f ( i ) и длиной основания xi .

18.

3. Предельный переход
Наконец, перейдем к пределу lim .
0
Определение. Если lim существует и не зависит от
0
А) способа разбиения отрезка [ a, b] на кусочки и от
Б) способа выбора средней точки,
то он называется определенным интегралом от функции f (x) на
b
отрезке [ a, b] и обозначается символом
f ( x)dx :
a
b
.
f ( x)dx = lim
0
a
Функция f (x) называется подынтегральной функцией, число а
нижним пределом интегрирования, а b – верхним пределом
интегрирования.

19.

Суммы Дарбу
Перейдем теперь к построению теории определенного
интеграла. Ее основой являются так называемые суммы Дарбу.
Пусть mi inf f ( x) и M i sup f ( x) есть наименьшее и
x [ xi , xi 1 ]
x [ xi , xi 1 ]
n 1
наибольшее значения функции на i-м кусочке. Суммы s mi xi и
n 1
i 0
S M i xi носят название нижней и верхней сумм Дарбу.
i 0
Так как mi f ( i ) M i , то s S при любом выборе средней
точки. Ясно также, что при фиксированном разбиении отрезка [a, b]
на кусочки s inf и S sup , где inf и sup берутся по
всевозможным выборам средних точек при заданном разбиении
отрезка [a, b] на кусочки.

20.

f (x)
m2
m1
s
m0
x
a = x0
x1
x2
b = x3
Геометрический смысл нижней суммы Дарбу.

21.

f (x)
M2
M1
M0
S
x
x2
b = x3
x1
a = x0
Геометрический смысл верхней суммы Дарбу

22.

Свойства сумм Дарбу
1. Если к имеющимся точкам деления добавить новые, то s
может только увеличиться, а S только уменьшиться.
Рассмотрим кусочек [ xk , xk 1 ] и представим себе, что на нем
появилась еще одна точка x , так что xk x xk 1 .
M''k
M'k
xk
x'
Mk
xk+1

23.

Пусть
M k sup
x [ xk , xk 1 ]
Так как
f ( x) , M k sup f ( x) и M k sup f ( x) .
x [ xk , x ]
x [ x , xk 1 ]
[ xk , x ] [ xk , xk 1 ] и [ x , xk 1 ] [ xk , xk 1 ],
то ясно, что M k M k и M k M k .
Рассмотрим отдельное слагаемое, скажем, верхней суммы
Дарбу, соответствующее отрезку [ xk , xk 1 ] . До добавления точки x
оно было равно M k ( xk 1 xk ) . После добавления точки x оно
превратилось
в
два
слагаемых
и
стало
равно
то
M k ( x xk ) M k ( xk 1 x ) . Так как M k M k и M k M k ,
M k ( x xk ) M k ( xk 1 x ) M k ( xk 1 xk ) и поэтому от добавления
точки x верхняя сумма Дарбу не могла возрасти. Аналогично
можно получить, что от добавления точки x нижняя сумма Дарбу
не могла уменьшиться.

24.

2. Каждая нижняя сумма Дарбу не превосходит любой верхней
суммы Дарбу, даже если они принадлежат различным разбиениям
отрезка [a, b] на кусочки.
s1 , S 1
s2, S 2
x
x
x
x
s3 , S 3

25.

В первом разбиении, очевидно, s1 S1 , во втором s2 S2 .
Объединим эти два разбиения в одно, смешав вместе все точки
деления (см. рис.). Тогда, учитывая свойство 1, получим
следующую цепочку неравенств
s1 s3 S3 S2 ,
откуда следует, что s1 S 2 , что и требовалось доказать.
Отсюда следует, что множество нижних сумм Дарбу {s},
соответствующих различным разбиениям отрезка [a, b] ограничено
сверху любой верхней суммой Дарбу, а множество верхних сумм
Дарбу {S } ограничено снизу любой нижней суммой Дарбу.
Поэтому существуют I* sup{ s} и I * inf{S}. Они носят название
нижнего и верхнего интегралов Дарбу. Очевидно, что для любого
разбиения отрезка [a, b] на
кусочки верно соотношение
s I* I * S .