Движение. Осевая симметрия

1.

2.

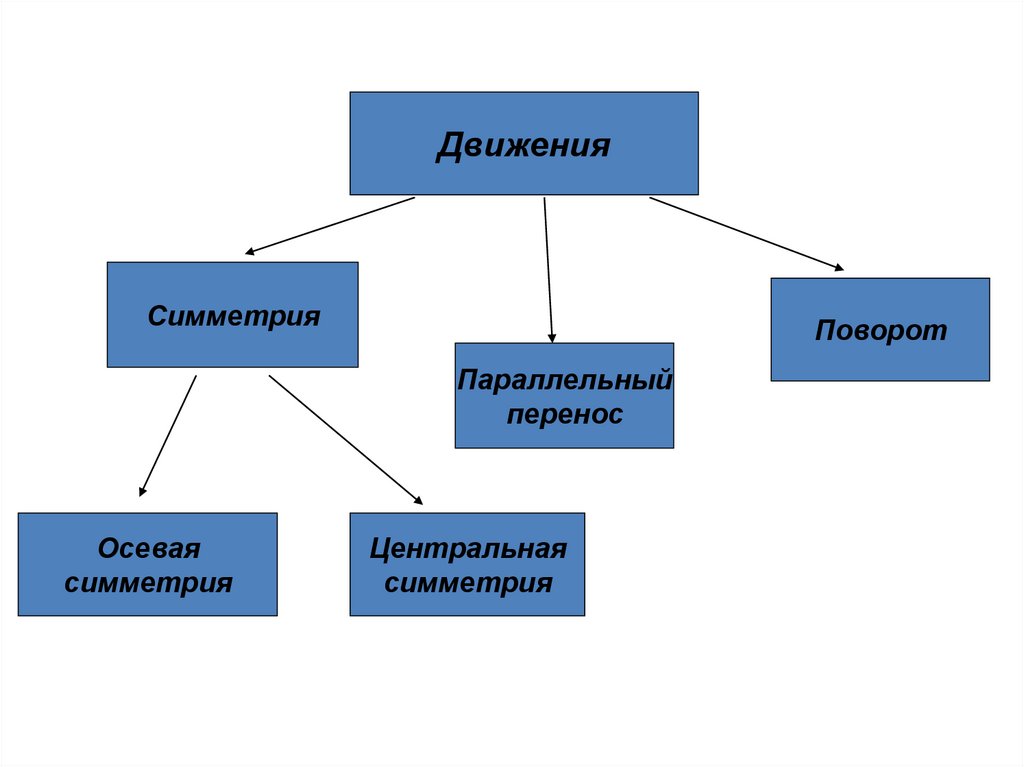
Движения
Симметрия
Поворот
Параллельный
перенос
Осевая
симметрия
Центральная
симметрия

3.

Осевая симметрия
Определение
Осевая симметрия –это
отображение плоскости на
себя, при котором каждая
точка М отображается в
такую точку М1, что отрезок
ММ1 перпендикулярен прямой
а (оси симметрии ) и отрезок
МР равен отрезку РМ1.

4.

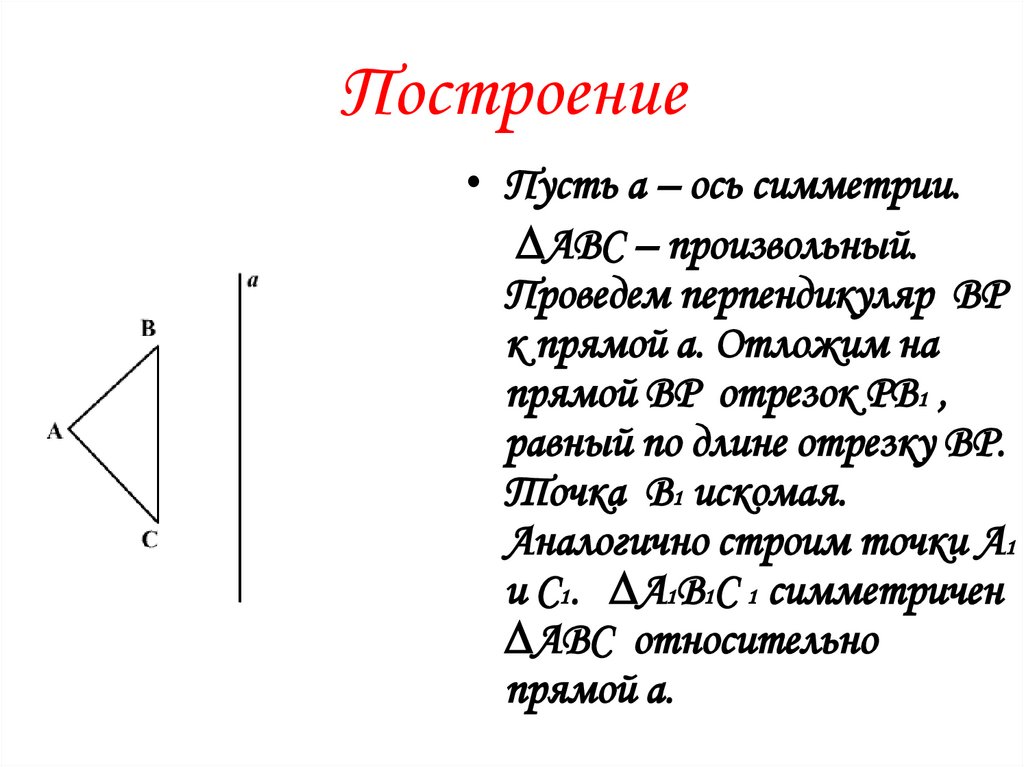
Построение
• Пусть а – ось симметрии.
∆АВС – произвольный.
Проведем перпендикуляр ВР
к прямой а. Отложим на
прямой ВР отрезок РВ1 ,
равный по длине отрезку ВР.
Точка В1 искомая.
Аналогично строим точки А1
и С1. ∆А1В1С 1 симметричен
∆АВС относительно
прямой а.

5.

6.

7.

Задача
Сколько осей симметрии имеет
равносторонний треугольник?
Сколько осей симметрии имеет квадрат?
Сколько осей симметрии имеет ромб, не
являющийся квадратом?
Начертите и убедитесь в
правильности своего ответа

8.

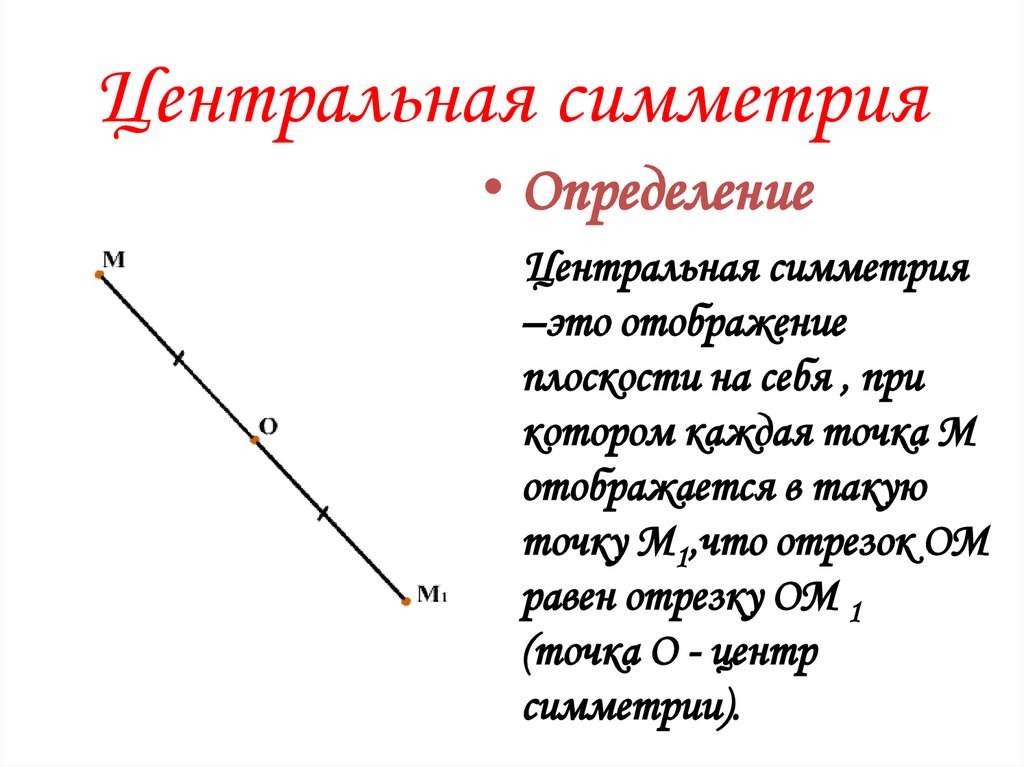
Центральная симметрия
• Определение
Центральная симметрия
–это отображение
плоскости на себя , при
котором каждая точка М
отображается в такую
точку М1,что отрезок ОМ
равен отрезку ОМ 1
(точка О - центр
симметрии).

9.

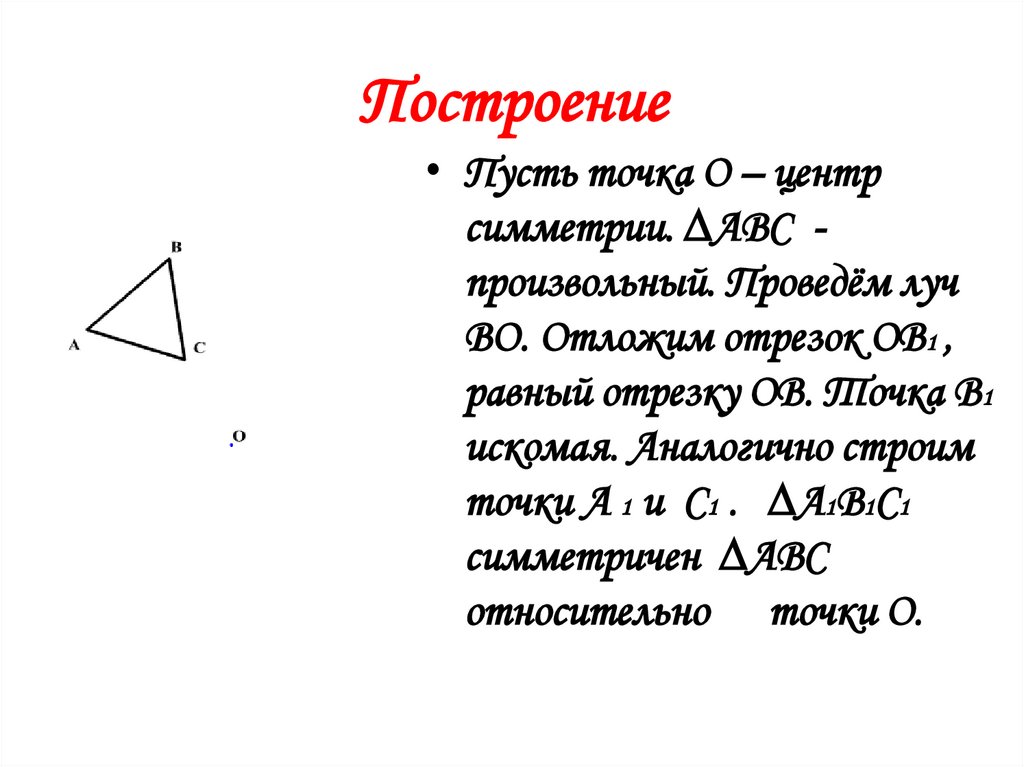
Построение
• Пусть точка О – центр
симметрии. ∆АВС произвольный. Проведём луч
ВО. Отложим отрезок ОВ1 ,
равный отрезку ОВ. Точка В1
искомая. Аналогично строим
точки А 1 и С1 . ∆А1В1С1
симметричен ∆АВС
относительно точки О.

10.

11.

12.

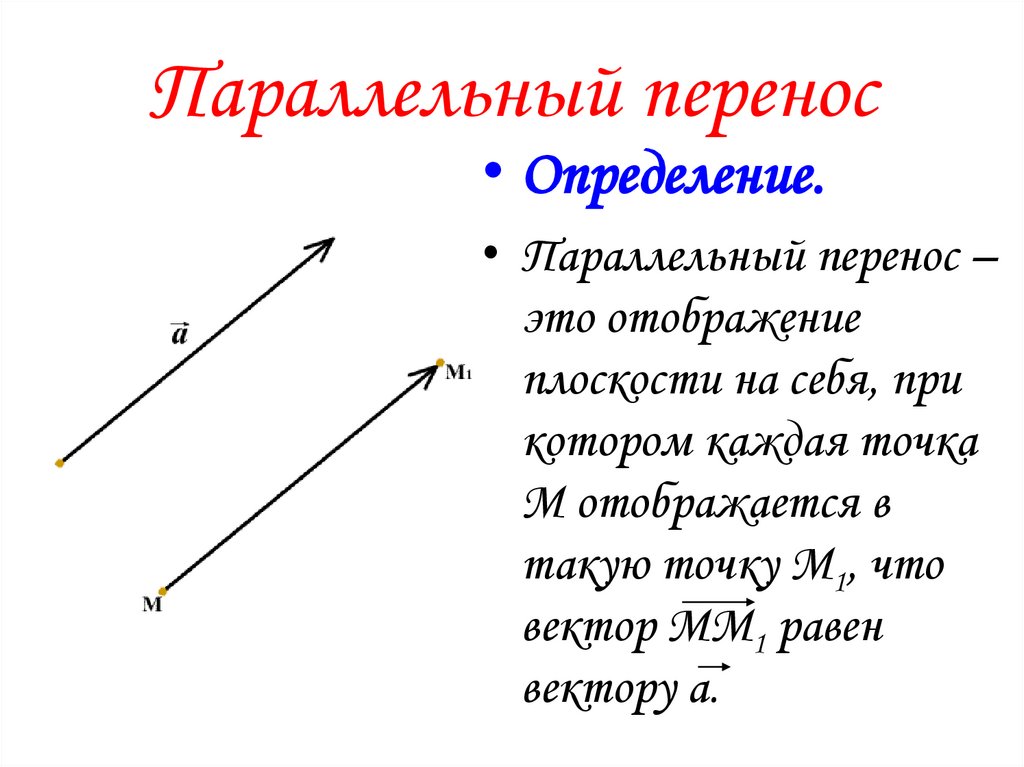
Параллельный перенос
• Определение.
• Параллельный перенос –
это отображение
плоскости на себя, при
котором каждая точка
М отображается в
такую точку М1, что
вектор ММ1 равен
вектору а.

13.

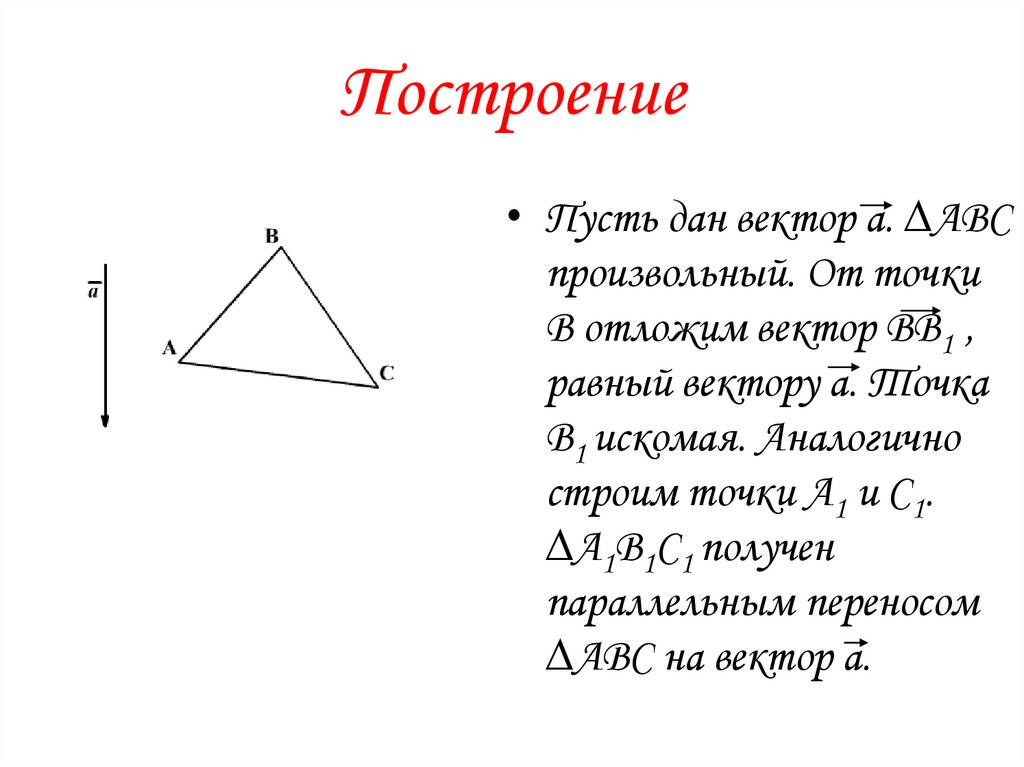
Построение
• Пусть дан вектор а. ∆АВС
произвольный. От точки
В отложим вектор ВВ1 ,
равный вектору а. Точка
В1 искомая. Аналогично
строим точки А1 и С1.
∆А1В1С1 получен
параллельным переносом
∆АВС на вектор а.

14.

15.

16.

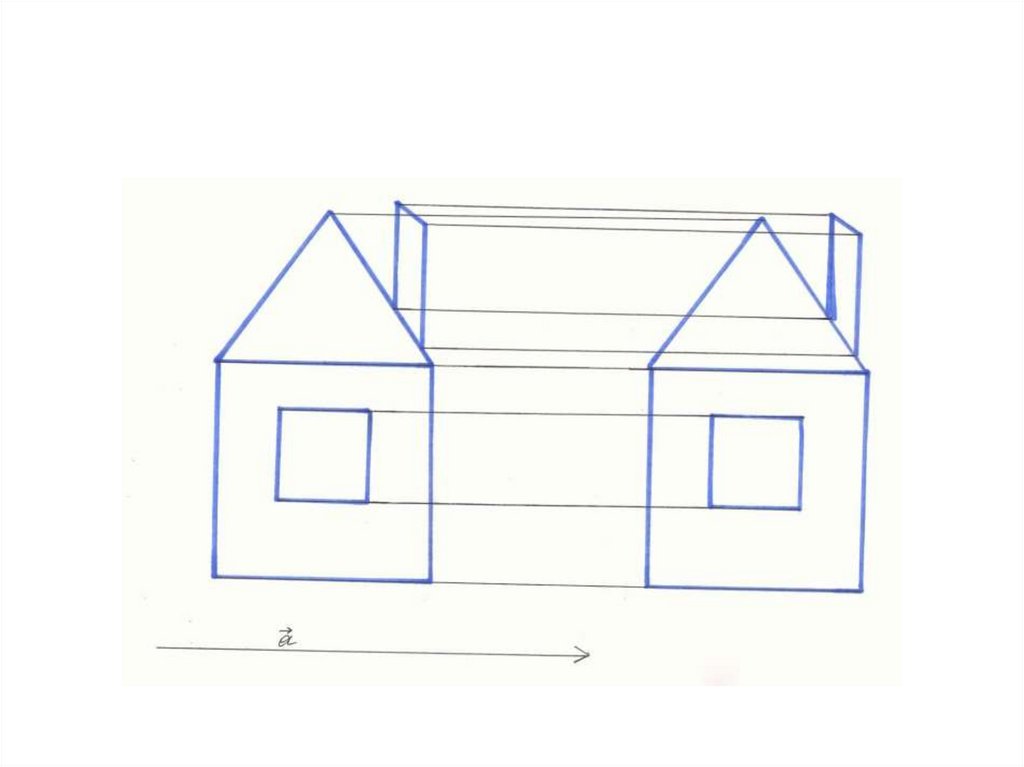
Движение в архитектуре.
Определить вид движения.
АКВИДУК

17.

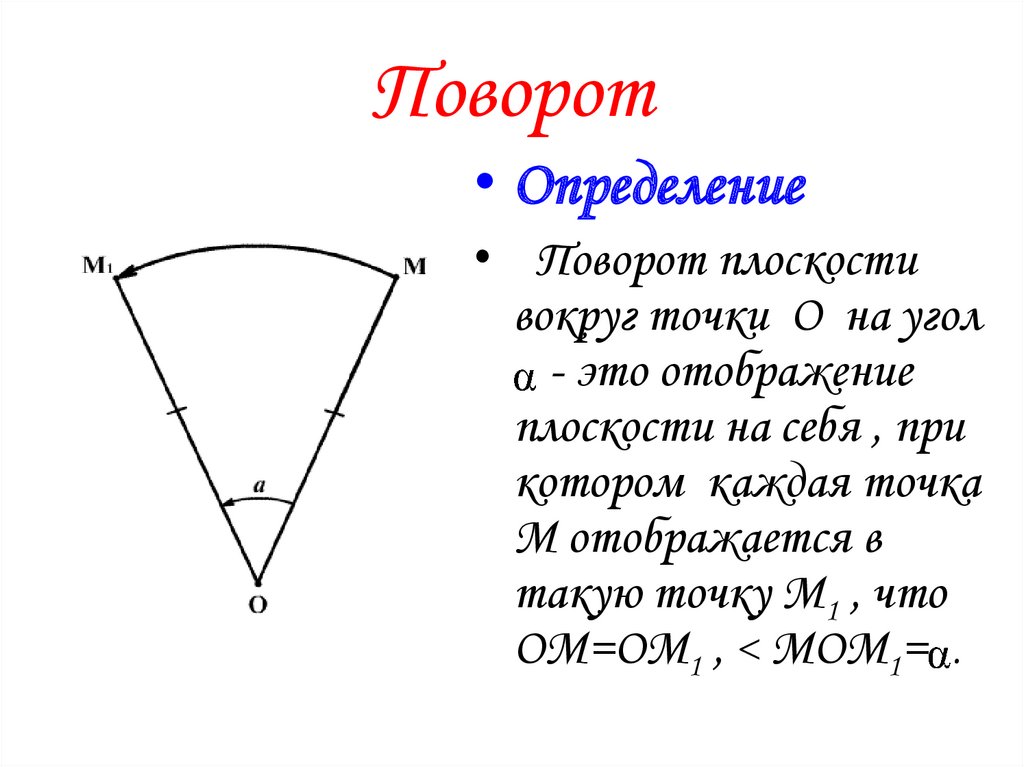
Поворот
• Определение
• Поворот плоскости
вокруг точки О на угол
- это отображение
плоскости на себя , при
котором каждая точка
М отображается в
такую точку М1 , что
ОМ=ОМ1 , < МОМ1= .

18.

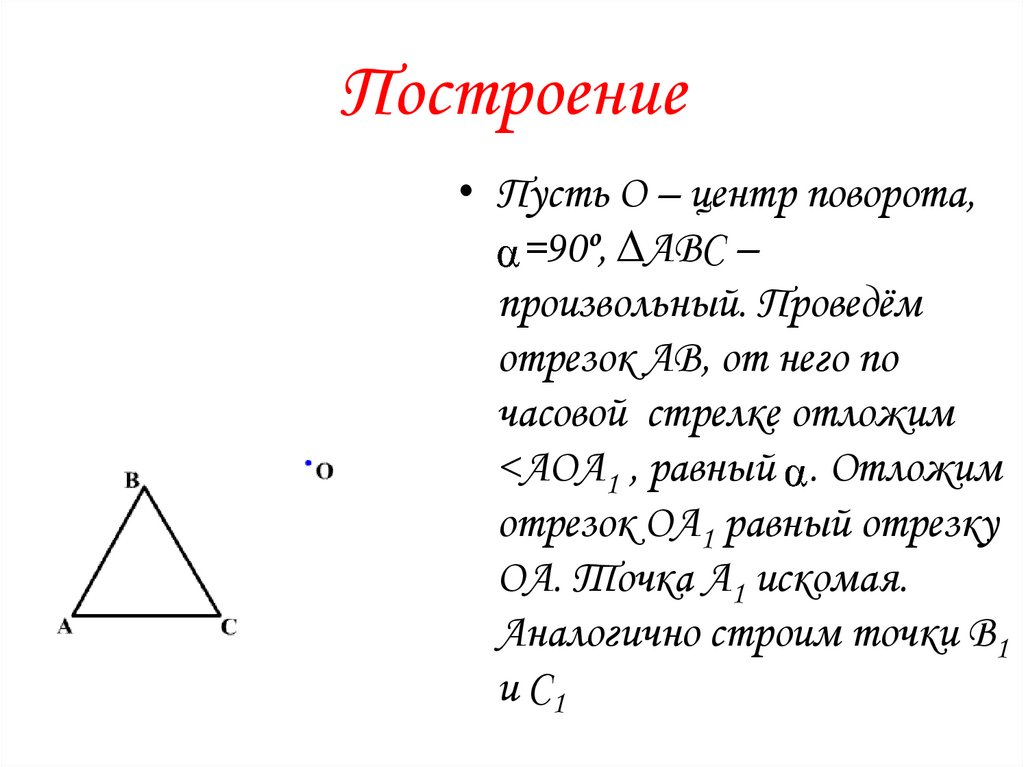
Построение
• Пусть О – центр поворота,
=90º, ∆АВС –
произвольный. Проведём
отрезок АВ, от него по
часовой стрелке отложим
<АОА1 , равный . Отложим
отрезок ОА1 равный отрезку
ОА. Точка А1 искомая.
Аналогично строим точки В1
и С1

19.

20.

21.

Вопросы
• Определить вид
симметрии.
• Что вам приходилось
встречать в природе из
известных видов
симметрии?

22.

Симметрия в природе

23.

24.

25.

Симметрия в архитектуре

26.

27.

Что происходит в алгебре?

28.

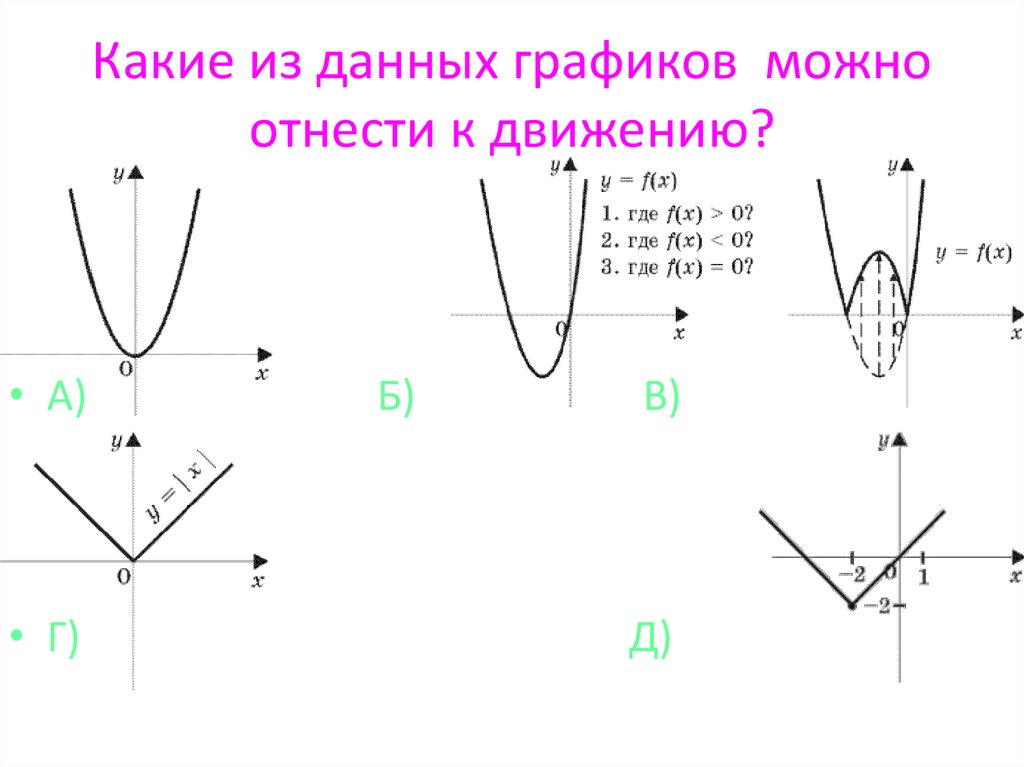
Какие из данных графиков можно
отнести к движению?
• А)
• Г)
Б)
В)
Д)

29.

Выполнение
практической работы
• Выполни работу на тот вид движения,
который тебе понравился.

30.

Выбери себе задание:
работа в парах
• С-11, вар. Б1,2 - №1
• С-12, вар. А1,2 - №1
• С-12, вар. Б1,2 - №2

31.

Какие виды движения мы
встречаем с вами в нашей
повседневной жизни?
Привлекла ли вас красота
симметрии, поворота и движения в
архитектуре?