Метод чувствительности в задачах оптимального проектирования осесимметричных деталей газотурбинного двигателя

1. ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования

МОСКОВСКИЙ ФИЗИКО-ТЕХНИЧЕСКИЙ ИНСТИТУТ
(государственный университет)
Применение метода чувствительности в задачах оптимального
проектирования осесимметричных деталей газотурбинного двигателя
________________________________________________________
Магистерская диссертация студента 865 группы ФАЛТ
Шутовой Марии Викторовны
Научный руководитель: доктор технических наук, профессор
Темис Юрий Моисеевич
Москва, 2014

2.

Содержание
• Постановка задачи
• Алгоритм метода чувствительности
• Описание программного комплекса
• Результаты расчетов
• Заключение
1/15

3.

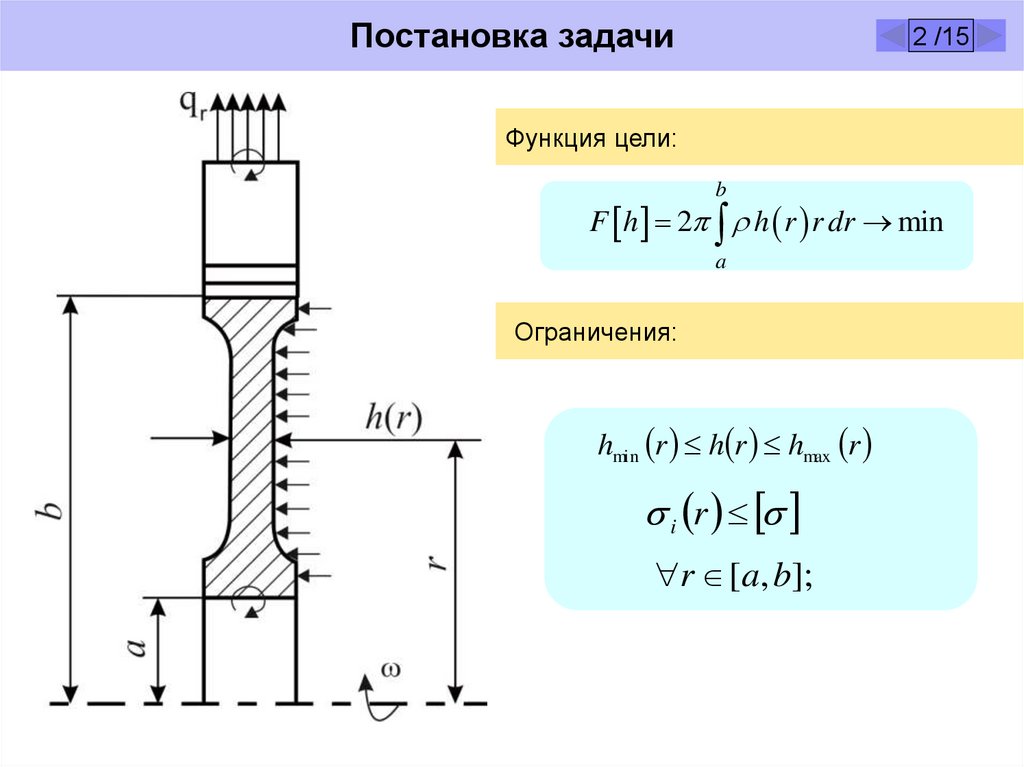
Постановка задачи
2 /15
Функция цели:
b
F h 2 h r r dr min
a
Ограничения:
hmin r h r hmax r
i r
r [a, b];

4.

Постановка задачи
Задача 1
Диск с
растягивающей
нагрузкой
du
1 1
u
Q 1 T ;
dr
r
Er h
dQ E
h u Q E T 2 r 2 h .
dr r
r
2
3 /15
Задача 2
Диск с
изгибающей
нагрузкой
S
d
1
dw
Mr T
dr
r
r
D
dr
dQ
Q
qz
dr
r
dM r D( 2 1)
S ( 1)
1
Q
Mr T
dr
r
r
r2

5.

Постановка задачи
4 /15
Диск с изгибающими и растягивающими нагрузками
du
1 2 1
u
Q 1 T ;
dr
r
Er h
dQ E
h u Q E T 2 r 2 h .
dr r
r
dw
S
d
1
dr
Mr T
dN
N
dr
r
r
D
qz
dr
r
Задача 3
Диск без учета
2
взаимного влияния dM r D( 1) Q 1 M ST ( 1)
r
нагрузок dr
r
r
r2
Задача 4 dw
d
1
M s T2 (1 )
Диск с учетом dr
dr
r
D
взаимного влияния du
1
u N s T1 (1 )
нагрузок dr
r
A
dM s
D(1 )
1
D(1 2 )T2
Q
M s ms
dr
r
r
r 22
2
dN s A 1
1
A 1
qr qz
2
u
N
T
s
1
dr
r 1 2
r 1 2
r (1 2 )
1 2
dQ
A(1 2 )
1
u Q
Ns F
2
2
dr
r 2 1 2 r
1
r
T1 A(1 ) qr qz
F F ( , , T )
r
1 2
1 2

6.

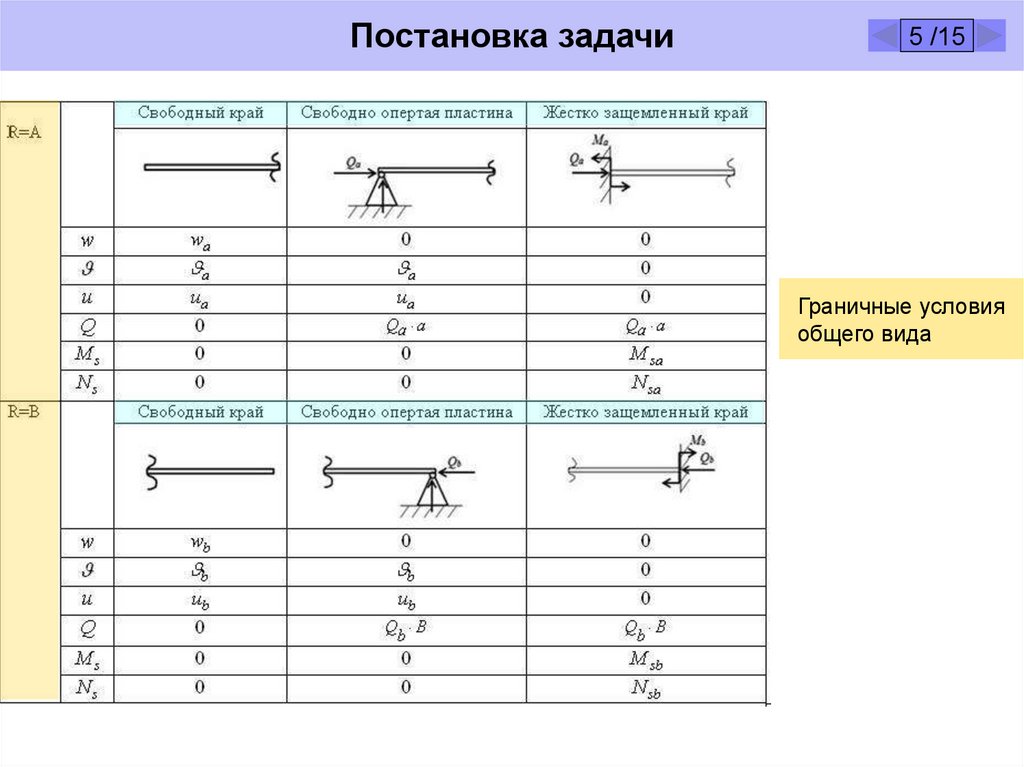
Постановка задачи
5 /15
Граничные условия
общего вида

7.

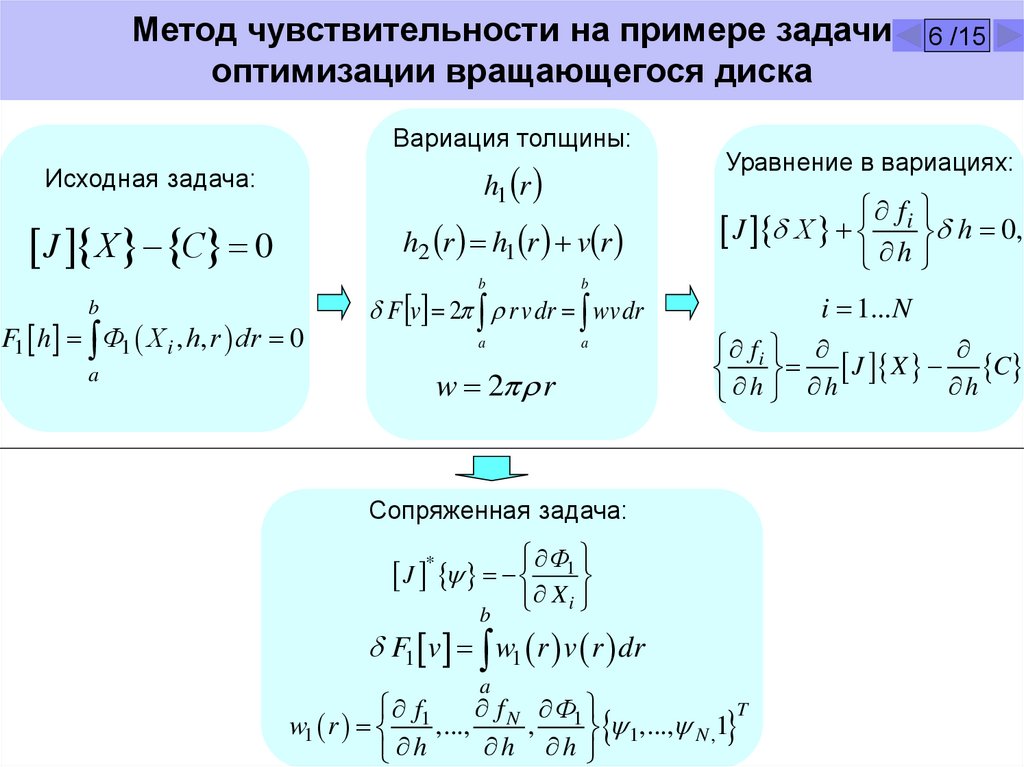
Метод чувствительности на примере задачи
оптимизации вращающегося диска
Вариация толщины:
Исходная задача:
h1 r
J Х C 0
h2 r h1 r v r
b
F1 h Ф1 Х i , h, r dr 0
a
b
b
a
a
F v 2 r v dr wv dr
w 2 r
Уравнение в вариациях:
fi
J Х h 0,
h
i 1...N
fi
J
X
C
h
h h
Сопряженная задача:
Ф1
Xi
J *
b
F1 v w1 r v r dr
a
6 /15
T
f
f Ф
w1 r 1 ,..., N , 1 1,..., N ,1
h h
h

8.

Метод чувствительности на примере задачи
оптимизации вращающегося диска
Задача нахождения минимума линейного функционала:
b
b
b
a
a
F h1 F v 2 h1 r rdr w r v r dr C w r v r dr min,
a
b
F1 h1 w1 r v r dr 0,
b
a
2
v
r
dr
0,
2
a
b
ww1dr
1
F
v r w ab
w1 b 1 w1
2
2
w
dr
w
dr
1
1
a
a
7 /15

9.

8 /15
Блок-схема алгоритма
Инициализация переменных,
ввод входных данных
Проверка выполнения
ограничений
i (r ) [ ]
Решение краевой задачи
J X C
Решение сопряжённой
краевой задачи
Ф
J
Хi
*
Условия
выполняются
Условия не
выполняются
S 0
S 0
Пересчёт толщин
b
ww1dr
F
v r S w ab
w1 b 1 w1
w12dr
w12dr
a
a
Расчёт градиента
f
f Ф
T
w1 r 1 ,.., N ,
1 ,.., N ,1
h h
h
Проверка сходимости алгоритма
Конец

10.

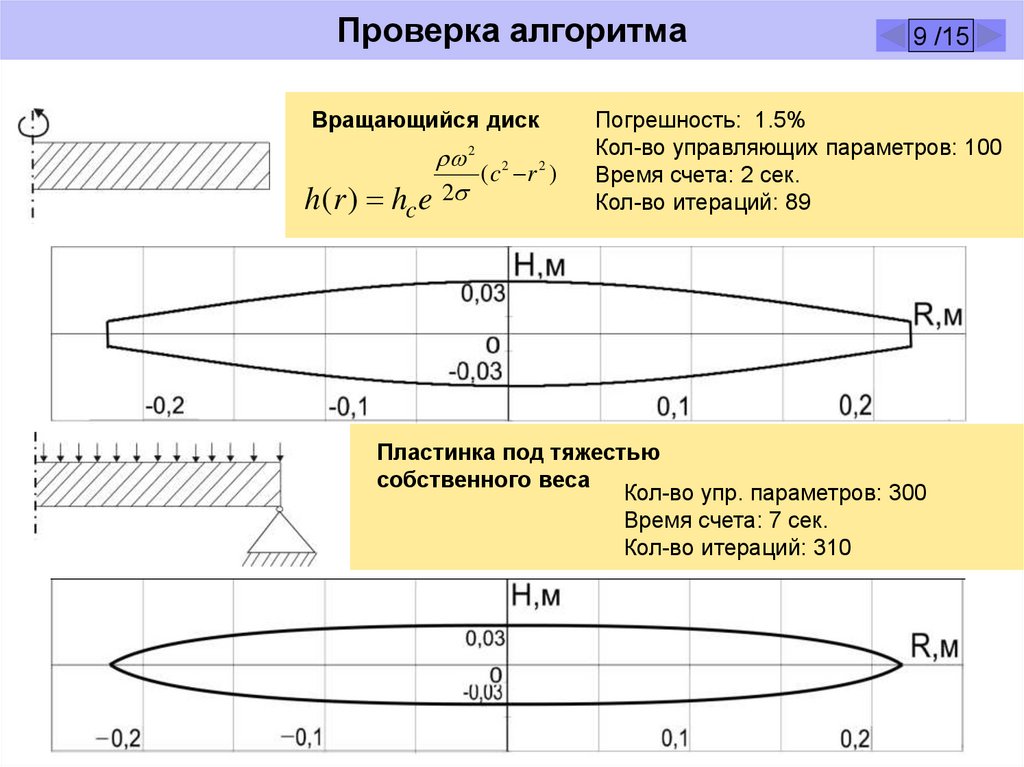
Проверка алгоритма
Вращающийся диск
h(r ) hc
2 2 2
(c r )
2
e
9 /15
Погрешность: 1.5%
Кол-во управляющих параметров: 100
Время счета: 2 сек.
Кол-во итераций: 89
Пластинка под тяжестью
собственного веса
Кол-во упр. параметров: 300
Время счета: 7 сек.
Кол-во итераций: 310

11.

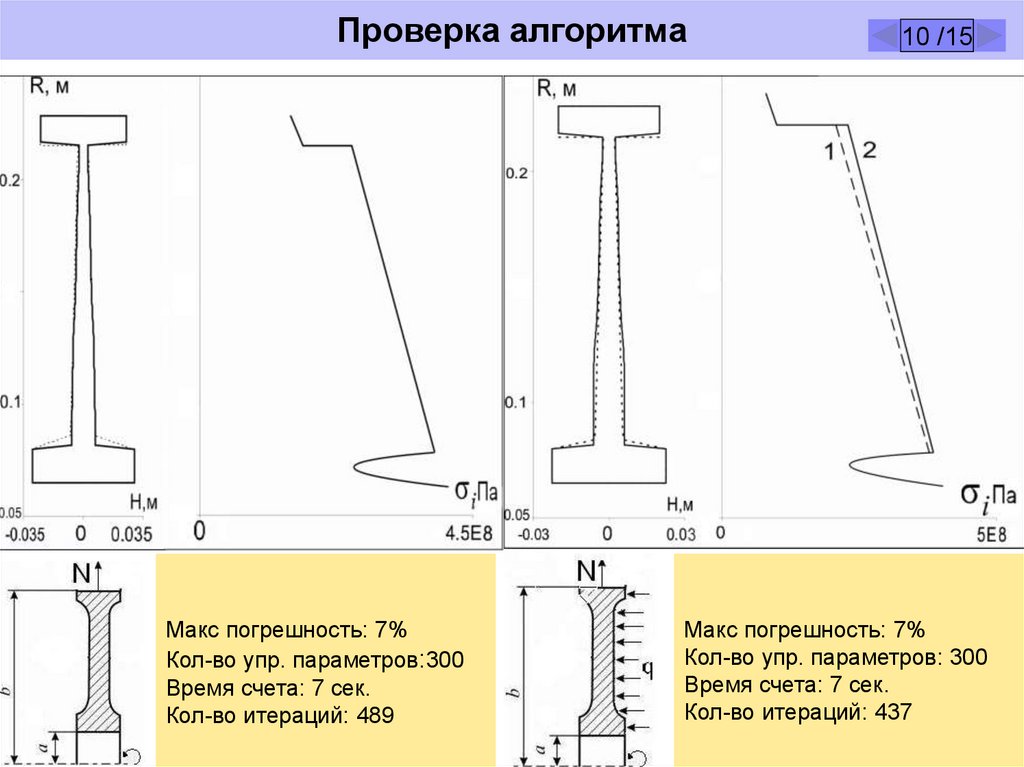
Проверка алгоритма
Макс погрешность: 7%
Кол-во упр. параметров:300
Время счета: 7 сек.
Кол-во итераций: 489
10 /15
Макс погрешность: 7%
Кол-во упр. параметров: 300
Время счета: 7 сек.
Кол-во итераций: 437

12.

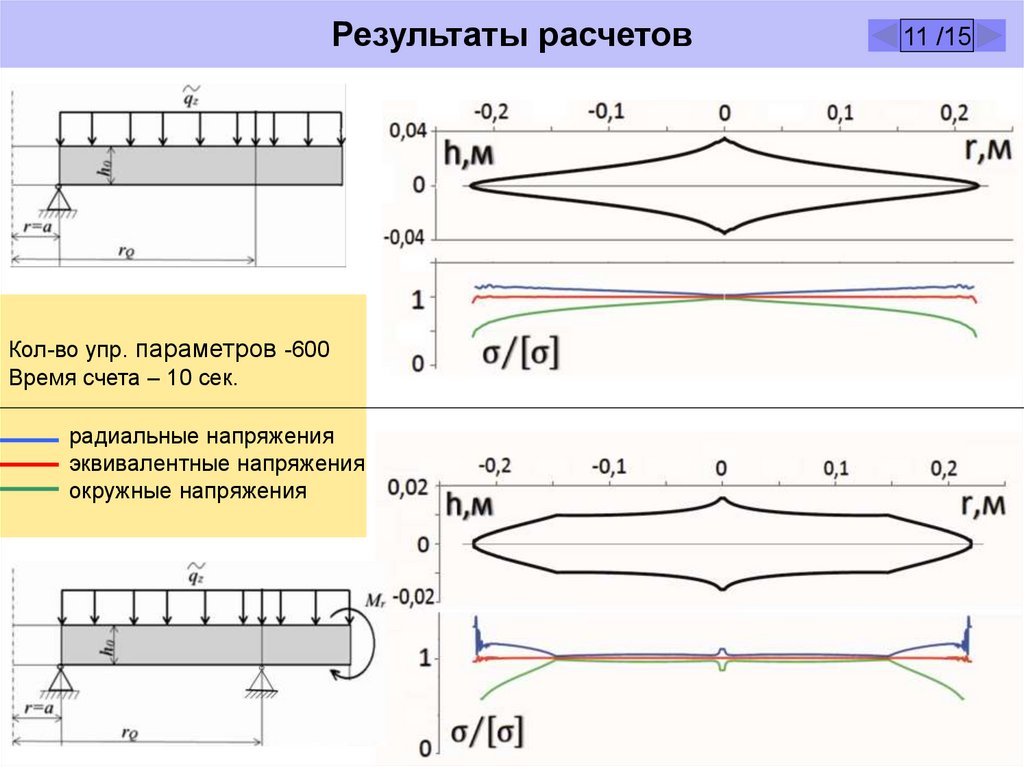
Результаты расчетов
Кол-во упр. параметров -600
Время счета – 10 сек.
радиальные напряжения
эквивалентные напряжения
окружные напряжения
11 /15

13.

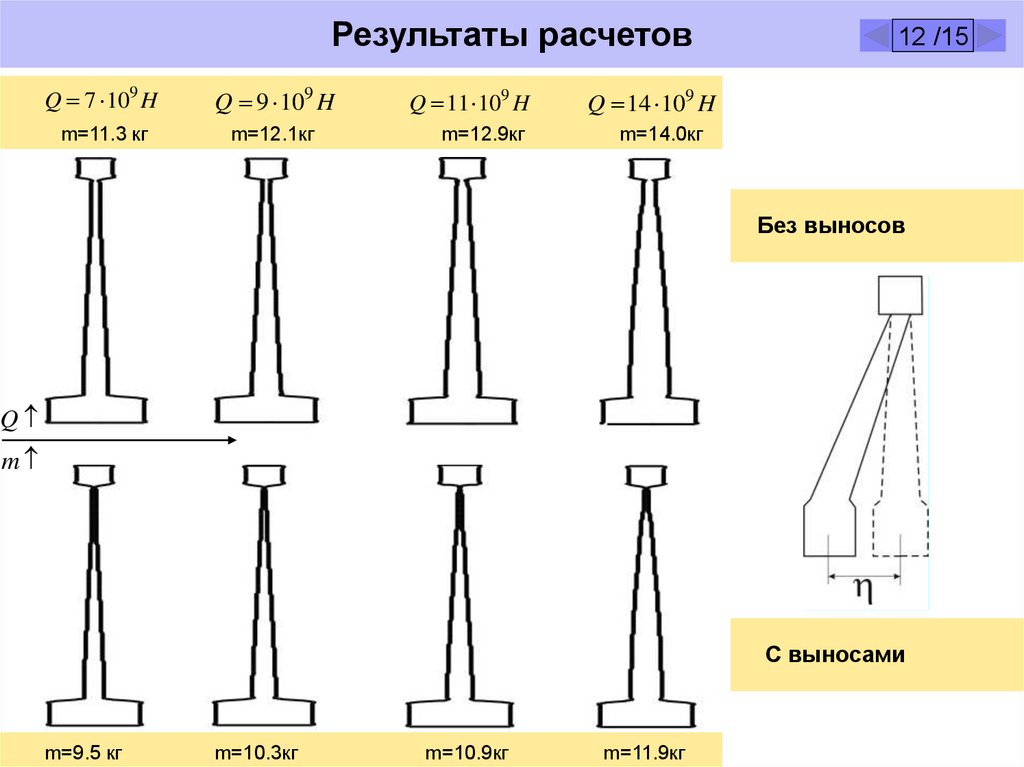
Результаты расчетов
Q 7 109 H
Q 9 109 H
m=11.3 кг
m=12.1кг
Q 11 109 H
m=12.9кг
12 /15
Q 14 109 H
m=14.0кг
Без выносов
Q
m
С выносами
m=9.5 кг
m=10.3кг
m=10.9кг
m=11.9кг

14.

Результаты расчетов
13 /15
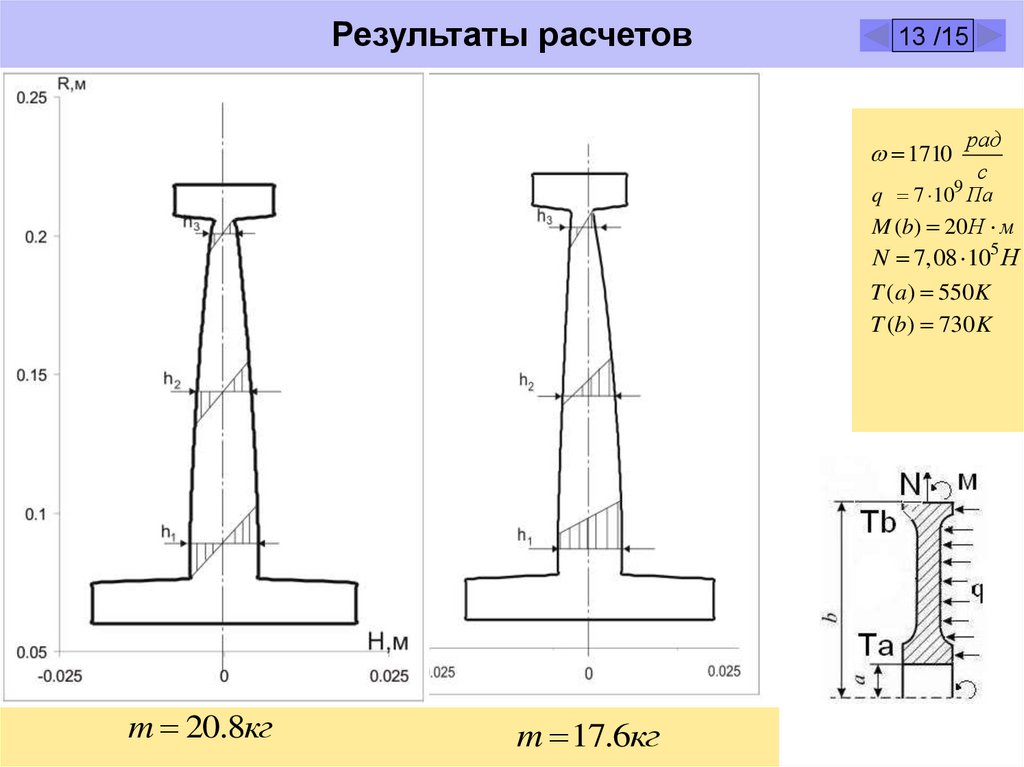
1710
рад
с
q 7 109 Па
M (b) 20 Н м
N 7,08 105 Н
T (a ) 550 K
T (b) 730 K
m 20.8кг
m 17.6кг

15.

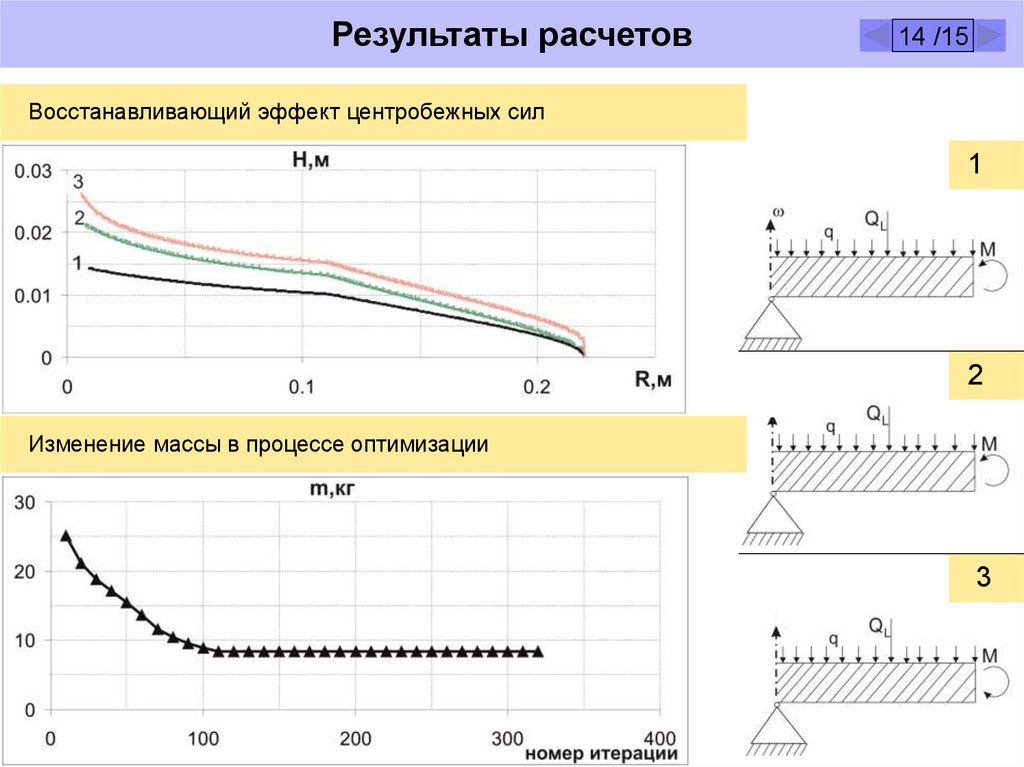
Результаты расчетов
14 /15
Восстанавливающий эффект центробежных сил
1
2
Изменение массы в процессе оптимизации
3

16.

Итоги
•Создана математическая модель расчета напряженно
деформированного состояния круглой пластинки переменной
толщины с различными комбинациями растягивающих и
изгибающих нагрузок
•Решена задача оптимизации формы круглой пластинки с
изгибающими и растягивающими нагрузками методом проекции
градиента.
•Реализован алгоритм метода проекции градиента, метода
конечных элементов и метода конечных разностей.
•Решена задача оптимизации формы круглой пластинки методом
проекции градиента с введением дополнительных ограничений на
максимальную (или минимальную) ширину пластинки и с
введением двух параметров управления (толщина пластинки и угол
подъема).
•В ходе выполнения работы написаны программы метода
чувствительности для оптимизации пластинки для четырех задач.
15 /15

17. Спасибо за внимание!