Частные производные. Лекция 17

1. Здравствуйте!

Лекция №17

2.

Частные производные
Пусть имеется функция п переменных f ( x1 , x 2 , ..., x n ) .
Изменим значение i-й переменной с xi на xi+ xi. Величина
i f f ( x1 , x 2 ,..., x i x i ,..., x n ) f ( x1 , x 2 ,..., x i ,..., x n )
называется частным приращением функции f (x) по i-й
переменной.
Величина
i f f ( x )
lim
f x ( x1 , x 2 ,..., x n )
x 0 x
x i
i
называется частной производной от функции f (x) по переменной
f ( x )
xi и обозначается либо символом
, либо символом f x ( x ) .
x i
Отметим главное: при вычислении частной производной по
какой-либо переменной все остальные переменные выступают
как константы.
i
i
i

3.

Вектор с компонентами
f
f f
,
, ...,
grad f
x n
x1 x 2
называется градиентом функции f (x) и обозначается символом
grad f .

4.

Полное приращение и дифференциал функции
Изменим теперь все переменные, заменяя x1 на x1 x1 , x 2 на
x 2 x 2 , …, x n на x n x n . Величина
f f ( x1 x1 , x 2 x 2 , ..., x n x n ) f ( x1 , x 2 , ..., x n )
называется полным приращением функции f (x).
Определение 1. Если f представима в виде
n
f Ai x i o ( ) ,
i 1
n
2
x
i ,
i 1
то функция f (x) называется дифференцируемой в точке х, а
комбинация
n
A x
i 1
i
i
df ( x )
называется
дифференциалом
(или,
точнее,
дифференциалом) функции f (x) и обозначается d f (x).
полным

5.

Определение 2. Если f представима в виде
n
f ( Ai i ) x i ,
i 1
где i 0 при 0 , то функция f (x) называется
дифференцируемой в точке х.
Можно доказать, что эти два определения эквиваленты.
Теорема 1. Если f (x) дифференцируема в точке х, то у нее в
этой точке существуют все частные производные и Ai f ( x ) x i .

6.

Доказательство. Дадим приращение хi только одной переменной
хi , а остальные переменные оставим без изменения. Тогда
i f ( Ai i ) x i ,
где i 0 при хi 0. Деля на хi
i f
Ai i
x i
и устремляя x i к нулю, получим
i f f
lim
Ai ,
x 0 x
x i
i
что и требовалось доказать.
i

7.

f
f
1 , а при j i
0 . Тогда из
x i
x j
общего выражения для дифференциала получим, что dx i x i .
Окончательно, выражение для дифференциала функции f (x)
приобретает вид
n
f
df dx i .
i 1 x i
Если ввести вектор dx ( dx1 , dx 2 , ..., dx n ) , то d f
можно
представить в виде
df (grad f , dx ) .
Если взять f ( x ) x i , то

8.

Теорема 2. Если частные производные f x i существуют не
только в точке x ( x1 , x 2 , x 3 ,... , x n ) , но и в некоторой ее
окрестности и непрерывны в точке х, то f (x) дифференцируема
в точке х.
Доказательство. Для простоты, окажем эту формулу только
для функции двух переменных f ( x , y ) .
Итак, пусть дана f ( x , y ) . Тогда ее приращение может быть
записано в виде
f ( x , y ) f ( x x , y y ) f ( x , y )
f ( x x , y y ) f ( x , y y ) f ( x , y y ) f ( x , y ) .
Заметим, что во второй скобке первые аргументы у f ( x , ...)
одинаковы. Поэтому, применяя формулу Лагранжа, получим
f ( x , y y ) f ( x , y ) f y ( x , y y ) y .
В силу непрерывности производной, можно записать
f y ( x , y y ) f y ( x , y ) ,
где 0 при у 0. Поэтому окончательно
f ( x , y y ) f ( x , y ) f y ( x , y ) y y .

9.

Аналогично, в первой скобке у f (..., y y ) одинаковым
является второй аргумент. Поэтому, по той же формуле Лагранжа,
f ( x x , y y ) f ( x , y y ) f x ( x x , y y ) x .
В силу непрерывности производной
f x ( x x , y y ) f x ( x , y ) ,
где 0 при ( x , y ) ( 0 , 0 ) . Поэтому
f ( x x , y y ) f ( x , y y ) f x ( x , y ) x x .
Объединяя все вместе, получим, что
f ( x , y ) f x ( x , y ) x f y ( x , y ) y ,
где и стремятся к нулю при ( x , y ) ( 0 , 0 ) . Это и
доказывает нашу теорему (см. определение 2).

10.

Производные от сложной функции
Пусть z f ( x1 , x 2 , ..., x n ) , а аргументы этой функции хi сами
являются функциями переменной t ( t1 , t 2 , ..., t m ) , то есть
z f ( x1 , x 2 , ..., x n ) , x i i ( t1 , t 2 , ..., t m ) .
Мы имеем, таким образом, дело со сложной функцией
z f ( 1 ( t ), 2 ( t ),..., n ( t )) .
Наша задача – научиться вычислять частные производны от z по tk,
то есть z t k .
Будем считать, что все частные производные f x i и i t k ,
i 1, n существуют и непрерывны. Отсюда будет следовать, что и
f ( x ) и все i (t ) дифференцируемы.
Изменим только одну из компонент из переменной t, скажем, tk,
сделав ей приращение tk. Но тогда уже все xi изменятся на
величины
xi i (t1 , t2 , ..., tk tk , ..., tm ) i (t1 , t2 , ..., tk , ..., tm ) .

11.

В силу дифференцируемости i (t ) , можно записать
i
x i
i t k ,
t k
где все i 0 при t k 0. Заметим, что поэтому и все xi 0 при
t k 0.
Но раз все xi изменились на величину xi, то z изменится на
величину
z f ( x1 x1 , x 2 x 2 , ..., x n x n ) f ( x1 , x 2 , ..., x n ) ,
и, в силу дифференцируемости f ( x ) , можно записать
n
f
z
i x i ,
i 1 x i
где i 0 когда все xi 0. Но так как при t k 0 как раз все xi 0,
то можно сказать, что все i 0 когда t k 0.

12.

Подставляя сюда выражение для xi, получим
n
n
f i
f
i
z
i
i t k
t k
i 1 x i
t k
i 1 x i t k
n
f
i
i
i
i i t k .
t k
x i
i 1
Но так как при t k 0 все i и i стремятся к нулю, то и величина
n
f
i i i
i i
t k
x i
i 1
стремится к нулю при t k 0.
Окончательно имеем
n
f i
z t k
t k ,
i 1 x i t k

13.

откуда получаем
n
f i
z
z
,
lim
t
0
t k
t k i 1 x i t k
что и даёт формулу для вычисления производной от сложной
функции от многих переменных
n
f i f 1 f 2
f n
z
.
...
t k i 1 x i t k x1 t k x 2 t k
x n t k
k

14.

Производная по направлению
Пусть задана функция f ( x ) , зависящая от п-мерной
переменной x ( x1 , x 2 , ..., x n ) и пусть в нашем п-мерном
пространстве задан вектор a ( a1 , a 2 , ..., a n ) единичной длины, то
n
есть
a
i 1
2
i
1.
x'
d(x, x ')
a
x

15.

Представим себе, что из точки х, двигаясь по вектору a (или в
противоположном направлении) мы перешли в точку x . При этом
мы сместились на расстояние d ( x , x ) (см. рис.).
Тогда производной от f ( x ) по направлению вектора a
называется величина
f ( x ) f ( x ) f
lim
.
x x
d ( x , x )
a
Знак «+» перед d ( x , x ) берется в том случае если мы двигались
по направлению вектора a , знак «–» – если мы двигались против
вектора a .

16.

Выведем формулу для f a . Так как вектор x x
коллинеарен вектору a , то их компоненты
пропорциональны, то есть
x n x n
x1 x1 x 2 x 2
...
t.
a1
a2
an
Обозначая это общее отношение через t, получим
xi xi ai t .
Находя d ( x , x ) , получим
d ( x , x )
n
n
i 1
i 1
2
2
2
(
x
x
)
t
a
i i
i t,
n
так как
2
a
i 1. Правильный знак перед d ( x , x ) учтен
i 1
тем, что t 2 записан как t.

17.

Тогда
f
f ( x1 a1t , x2 a2t , ..., xn an t ) f ( x1 , x2 , ..., xn )
lim
t
0
a
t
d
f ( x1 a1t , x2 a2t , ..., xn an t ) .
dt
t 0
Используя формулу для производной от сложной
функции и учитывая, что d ( x i a i t ) dt a i , получим
n
n
f ( x1 a1 t , x 2 a 2 t , ..., x n a n t )
f
f ( x )
ai
ai
a i 1
x i
i 1 x i
t 0

18.

d
gra
f
a
df /da
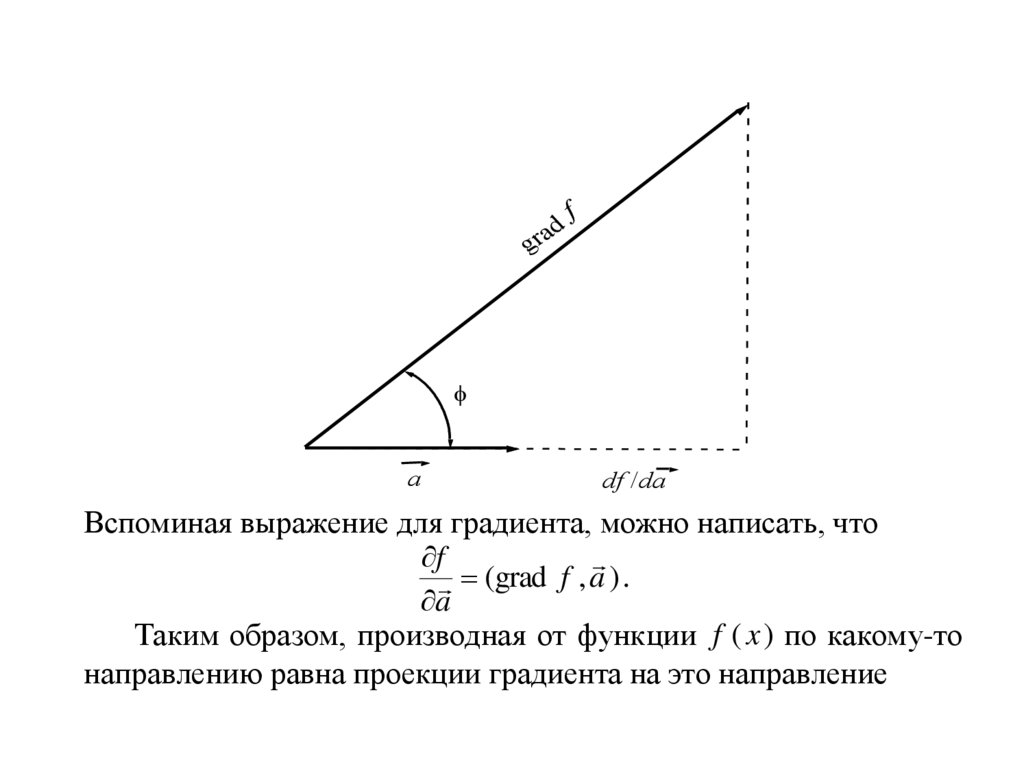
Вспоминая выражение для градиента, можно написать, что
f
(grad f , a ) .
a
Таким образом, производная от функции f ( x ) по какому-то
направлению равна проекции градиента на это направление

19.

Вспоминая, что a 1 и обозначая через угол между
векторами a и grad f, можно записать, что
f
grad f cos .
a
Так как 1 cos 1, то
f
max grad f (получается при = 0),
a
f
min grad f (получается при = ).
a
Глядя на эти формулы можно сказать следующее:
вектор grad f указывает нам, в каком направлении функция
возрастает быстрее всего: функция быстрее всего возрастает при
движении по направлению вектора градиента и быстрее всего
убывает при движении против направления градиента.

20.

Заметим, в заключение, что если вектор a имеет произвольную
длину, то
f (grad f , a )
,
a
a
так как вектор a a имеет единичную длину и направлен в ту же
сторону, что и вектор a .