Похожие презентации:
Пространственный вектор потокосцепления ротора АД
1.
Пространственный вектор потокосцепления ротора АДra l r ira lmr (irb irc ) lmsr [isa cos
isb cos( 120) isc cos( 240)]
rb l r irb lmr (ira irc ) lmsr [isa cos( 240) isb cos
isc cos( 120)]
rc l r irc lmr (ira irb ) lmsr [isa cos( 120) isb cos( 240) isc cos ]
r
lr
2
r ra a1 rb a2 rc a3
3
lmsr
r lr lmr lmsr
2.
23
2
3
1
I mr j ( t ir )
e
1 e j ( t ir ) 1 1 e j 0
2
a1
ira
lr lr ira a1 irb a2 irc a3 lr
2
I mr j ( t ir ) j120
I
e
e
e j ( t ir ) e j120 1 e j120 mr e j ( t ir ) e j 240 e j ( t ir ) e j 240 1 e j 240
2
2
a2
a3
i
i
rc
rb
1
lr I mr e j ( t ir ) 1 e j 0
e j ( t ir ) 1 e j 0
3
1
e j ( t ir ) 1 e j ( 120 120) e j ( t ir ) 1 e j (120 120)
2
480 360 120
e j ( t ir ) 1 e j ( 240 240) e j ( t ir ) 1 e j (240 240)
3 1 e j0
lmr
0
1
2
lr I mr 1 e j ir e j t lr I r
Ir
2
2
lmr [(irb irc ) a1 (ira irc ) a2 (ira irb ) a3 ] lmr [ira a1 irb a2 irc a3 ] lmr I r
3
3
ira
irb
irc
где ira irb irc 0 - соединение статорной обмотки в
“
“
3.
lmsr2
Ar B r C r
3
Ar a1 lmsr isa cos isb cos 120 isc cos 240
1
1
I
I
1 e lmsr ms e j ( t is ) 1 e j ( t is ) 1 e j e j ms e j ( t is ) e j120 e j ( t is ) e j120
2
2
2
isa
cos
isb
1 j j120 j j120 2 I ms j ( t is ) j 240 j ( t is ) j 240 1 j j 240 j j 240 I ms
j0
e e
e e
e
e
e
e
e e
e e
1
e
lmsr
2
2
2
4
cos( 120)
isc
cos( 240)
j0
[ e j ( t is ) e j
1
2
1
e j ( t is ) e j
1
e j ( t is ) e j
e j ( t is ) e j e j (120 120) e j ( t is ) e j e j ( 120 120) e j ( t is ) e j
e j ( t is ) e j e
120
j (240 240)
e j ( t is ) e j e j ( 240 240) e j ( t is ) e j
0
3
3
3
lmsr e j I ms 1 e j is e j t lmsr I ms e j ( t is ) e j 1 e j 0
4
4
Is
1
e j (120 120 )
1
e j ( t is ) e j e j (120 120)
2
e j ( t is ) e j
1
e j (240 240) e j ( t is ) e j e j (240 240) ]
3
0
4.
Ar a1 lmsr isa cos isb cos 120 isc cos 2401
I
1
j
(
t
)
j
(
t
)
j
j
ms
is
is
1 e lmsr
e
1 e
1 e e
2
2
isa
cos
2
I ms j ( t is ) j120
1
j ( t is )
j120
j
j120
j
j120
e
e
e
e e e
e e
2
2
isb
cos( 120)
j0
I ms j ( t is ) j 240 j ( t is ) j 240 1 j j 240
j
j 240
e
e
e
e
e e
e e
2
2
isc
cos( 240)
5.
I ms1 e j 0 lmsr
4
j ( t is )
j
[ e
e
1
2
e
e
j ( t is )
j ( t is )
e
e
j
j
1
e
e
j (120 120)
120
j (240 240)
0
e
j ( t is )
e
j ( t is )
e
j ( t is )
e
j
e
j
e
j
1
e
e
j ( 120 120)
e
e
j ( 240 240)
e
3
6.
Ar a1 lmsr isa cos isb cos 120 isc cos 2401
I
1
j
(
t
)
j
(
t
)
j
j
ms
is
is
1 e lmsr
e
1 e
1 e e
2
2
isa
cos
2
I ms j ( t is ) j120
1
j ( t is )
j120
j
j120
j
j120
e
e
e
e e e
e e
2
2
isb
cos( 120)
j0
I ms j ( t is ) j 240 j ( t is ) j 240 1 j j 240
j
j 240
e
e
e
e
e e
e e
2
2
isc
cos( 240)
7.
ee
j ( t is )
j ( t is )
e
j ( t is )
e
j
e
j
e
j
1
e
j (120 120)
e
j (240 240)
3
e
j ( t is )
e
j ( t is )
e
j ( t is )
e
j
e
j
e
j
1
e
j (120 120)
2
e
j (240 240)
]
1
0
3
3
j is
j ( t is )
j
j t
j
lmsr e I ms 1 e
e 1 e j0
e lmsr I ms e
4
4
Is
8.
B r a2 lmsr isa cos 240 isb cos isc cos 1201
I
1
I
j
(
t
)
j
(
t
)
j
j
240
j
j
240
is
is
1 e lmsr ms e
1 e
1 e e
e e ms e j ( t is ) e j120 e j ( t is ) e j120
2
2
2
isa
isb
cos 240
2 I
1 j
1
j
e e ms e j ( t is ) e j 240 e j ( t is ) e j 240 e j e j120 e j e j120
2
2
2
cos
isc
cos( 120)
j120
I ms
1 e j120 lmsr
4
[ e j ( t is ) e j e j 240
e j ( t is ) e j e j 240
e j ( t is ) e j e j 240
e j ( t is ) e j e j 240
1
e j ( t is ) e j e j120
e j ( t is ) e j e j120
e j ( t is ) e j e j120
e j ( t is ) e j e j120
2
1
2
e j ( t is ) e j e
0
j (240 120)
240-360=-120
||
-240+360=120
||
0
j (240 120)
e j ( t is ) e j e j (240 120) e j ( t is ) e j e j (240 120) e j ( t is ) e j e
0
0
3 e j120
3 e j120
3
3
lmsr e j I ms 1 e j120 e j120 e j is e j t lmsr I ms e j ( t is ) e j 1 e j120 e j120
4
4
j0
1 e
3
3
lmsr e j I ms 1 e j is e j t lmsr I ms e j ( t is ) e j 1 e j 240
4
4
Is
]
9.
B r a2 lmsr isa cos 240 isb cos isc cos 1201
I
1
1 e j120 lmsr ms e j ( t is ) 1 e j ( t is ) 1 e j e j 240 e j e j 240
2
2
isa
cos 240
2
I ms j ( t is ) j120 j ( t is ) j120 1 j
j
e
e
e
e
e e
2
2
isb
cos
I ms j ( t is ) j 240 j ( t is ) j 240 1 j j120 j j120
e
e
e
e
e e
e e
2
2
isc
cos( 120)
10.
22
2
cos
isc
I ms
j120
1 e
lmsr
4
j ( t is )
j
j 240
[ e
e e
1
2
e
e
j ( t is )
j ( t is )
e
e
j
j
e
e
j120
0
j (240 120)
c
240-360=-120
||
e
j ( t is )
e
j ( t is )
e
j ( t is )
e
j
e
j
e
j
e
j 240
e
e
j120
e
j (240 120)
e
e
j120
0
3 e
3
3
j
j
j
120
j
120
j
t
is
e e lmsr I ms
lmsr e I ms 1 e e
4
4
j0
11.
B r a2 lmsr isa cos 240 isb cos isc cos 1201
I
1
1 e j120 lmsr ms e j ( t is ) 1 e j ( t is ) 1 e j e j 240 e j e j 240
2
2
isa
cos 240
2
I ms j ( t is ) j120 j ( t is ) j120 1 j
j
e
e
e
e
e e
2
2
isb
cos
I ms j ( t is ) j 240 j ( t is ) j 240 1 j j120 j j120
e
e
e
e
e e
e e
2
2
isc
cos( 120)
12.
-240+360=120||
e
j ( t is )
e
j ( t is )
e
j ( t is )
e
j
e
j 240
e
j
e
j120
e
j
e
j ( t is )
e
j ( t is )
j ( t is )
j (240 120)
e
j
e
j 240
e
j
e
j120
j
0
j (240 120)
1
2
e
e
e
e
]
j120
0
3 e
3 j ( t j is ) j j120 j120
3
j
j ( t )
j120 j120
j t
j
j120
j120
e lmsr I ms e
e 1 e e
I ms elmsr e I ems 1 e 1 ee ee
4
4
j0
is
1 e
is
3
3
j is
j ( t is )
j
j t
j
j 240
j lmsr ej 240 I ms 1 e
e
l
I
e
e
1
e
4 msr ms
e 4 1 e
Is
13.
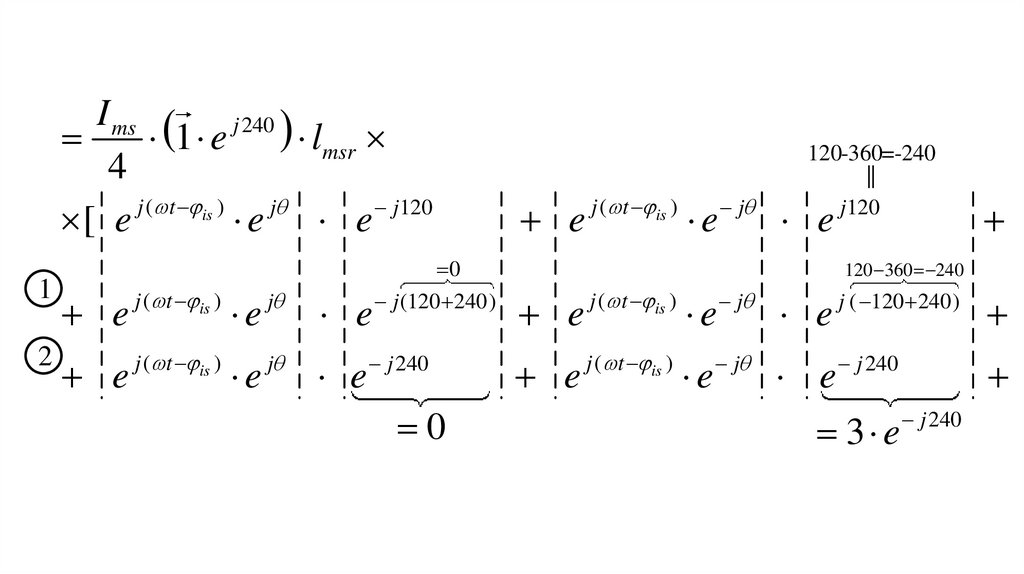
C r a3 lmsr isa cos 120 isb cos 240 isc cos1
I
1
I
j
(
t
)
j
(
t
)
j
j
120
j
j
120
ms
is
is
1 e lmsr
e
1 e
1 e e
e e ms e j ( t is ) e j120 e j ( t is ) e j120
2
2
2
isa
isb
cos 120
1 j j 240 2 j j 240 I ms j ( t is ) j 240 j ( t is ) j 240 1 j
e e
e e
e
e
e
e
e e j
2
2
2
i
cos
cos 240
sc
I
ms 1 e j 240 lmsr
120-360=-240
4
||
[ e j ( t is ) e j e j120
e j ( t is ) e j e j120
e j ( t is ) e j e j120
e j ( t is ) e j e j120
j 240
1
2
e j ( t is ) e j e
120 360 240
e j ( t is ) e j e j ( 120 240) e j ( t is ) e j e
e
j
e
j 240
e
j ( t is )
e
j
j 240
j ( t is )
120
j (120 240)
= -120
j 240
e j ( t is ) e j e
0
j (120 240)
e
e
e e
e j ( t is ) e j e j 240
0
0
3 e j 240
3 e j120
3
3
lmsr e j I ms 1 e j 240 e j 240 e j is e j t lmsr I ms e j ( t is ) e j 1 e j 240 e j120
4
4
j0
1 e
3
3
lmsr e j I ms 1 e j is e j t lmsr I ms e j ( t is ) e j 1 e j120
4
4
Is
e
j ( t is )
0
j (120 240)
j
1
2
]
14.
C r a3 lmsr isa cos 120 isb cos 240 isc cos1
I ms j ( t is )
j ( t is )
j
j120
j
j120
1 e
lmsr
e
1 e
1 e e
e e
2
2
isa
cos 120
2
I ms j ( t is ) j120
1
e
e
e j ( t is ) e j120 e j e j 240 e j e j 240
2
2
isb
cos 240
j 240
I ms j ( t is ) j 240
1
j ( t is )
j 240
j
j
e
e
e
e
e e
2
2
isc
cos
1
15.
22
cos 240
isc
I ms
j 240
lmsr
1 e
4
j ( t is )
j120
j
e e
[ e
1
2
e
j ( t is )
j ( t is )
e
j
j
e
0
j (120 240)
j 240
e
j ( t is )
e
j
120-360=-240
||
j120
e
e
120 360 240
e
j ( t is )
j ( t is )
e
j
j
e
j ( 120 240)
j 240
e
e
j 240
0
3 e
3
3
j
t
j
240
j
240
j
j
is
e e lmsr I ms
lmsr e I ms 1 e e
4
4
j0
e
e
e
e
e
16.
C r a3 lmsr isa cos 120 isb cos 240 isc cos1
I ms j ( t is )
j ( t is )
j
j120
j
j120
1 e
lmsr
e
1 e
1 e e
e e
2
2
isa
cos 120
2
I ms j ( t is ) j120
1
e
e
e j ( t is ) e j120 e j e j 240 e j e j 240
2
2
isb
cos 240
j 240
I ms j ( t is ) j 240
1
j ( t is )
j 240
j
j
e
e
e
e
e e
2
2
isc
cos
1
17.
ej ( t is )
e
j ( t is )
j ( t is )
e
e
j
j
j
e
j 120
e
e
120
j (120 240)
= -120
j 240
j ( t is )
e
j ( t is )
j ( t is )
e
j
e
j
e
e
j
j 120
0
j (120 240)
1
2
]
e
e
e
e
j120
0
3 e
3 j ( j t ) j j 240 j 240j 240 j j120
j ( t )
j t 3
j
j 240 j120
is
l
e
I
1
e
e
e
e
l
I
e
e
1
e
e
4 msr ms
I ms4 emsr ms e 1 e e
1 e j 0
e
e
is
3
j is
j ( t is )
j
j t 3
j
j lmsr e j120
e 1 e j120
I ms 1 e e lmsr I ms e
4
e 4 1 e
Is
j 240
is
18.
lmsr2 9
3
j ( t is )
j
j
j0
j 240
j120
lmsr e I s lmsr I ms e
e 1 e 1 e 1 e
3 4
4
0
3
lmsr e j I s
2
2
3
r ra a1 rb a2 rc a3 lr lmr lmsr lr I r lmr I r lmsr e j I s
3
2
3
j
lr lmr I r lmsr e I s Lr I r Lm e j I s
2
Lr
L
m
r Lr I r Lm e j I s



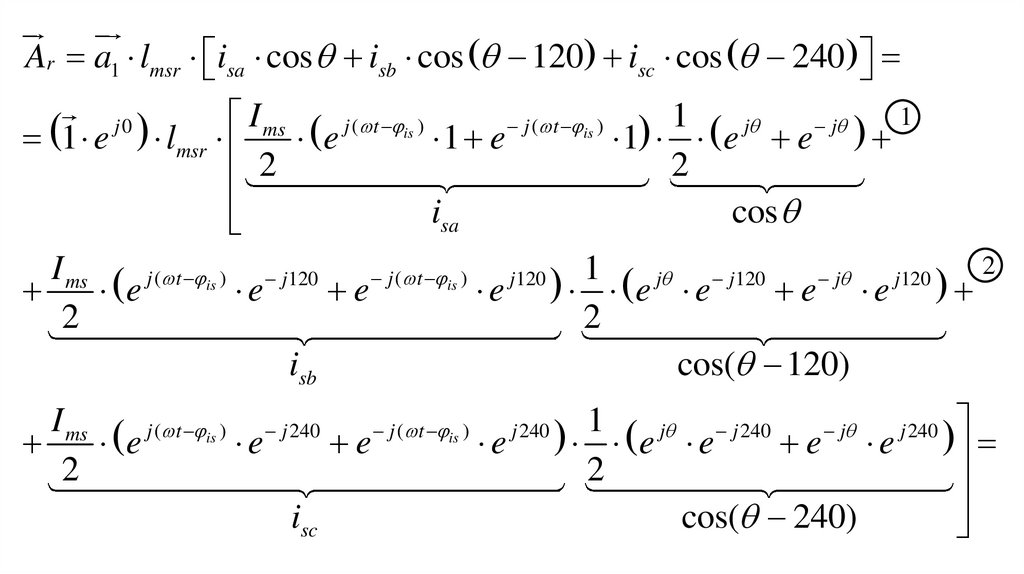

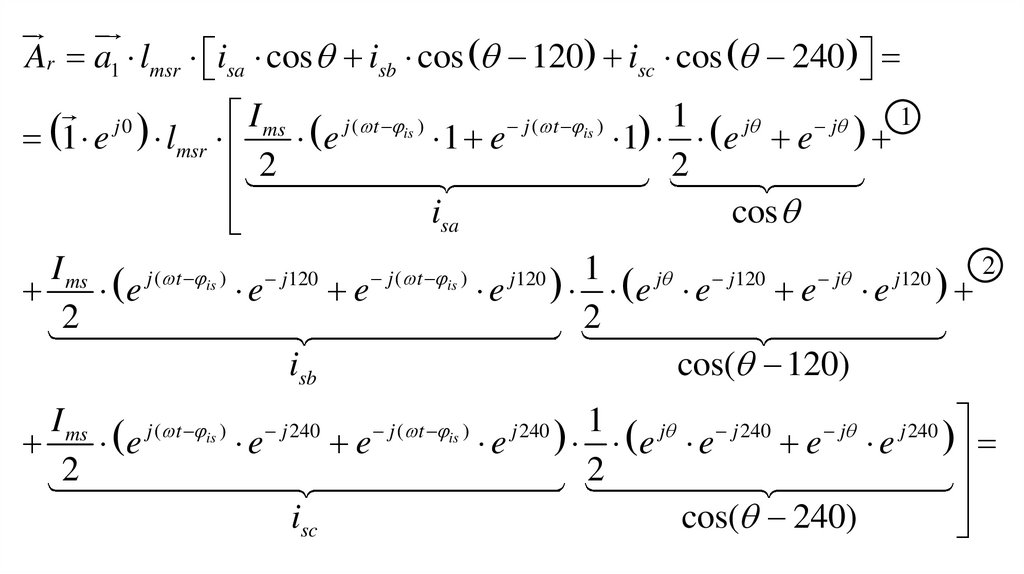
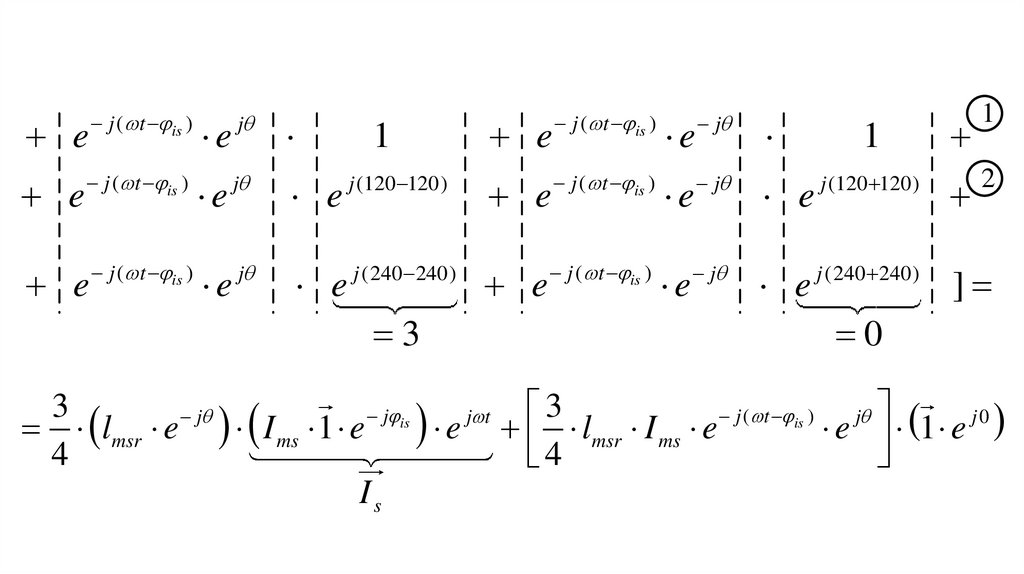

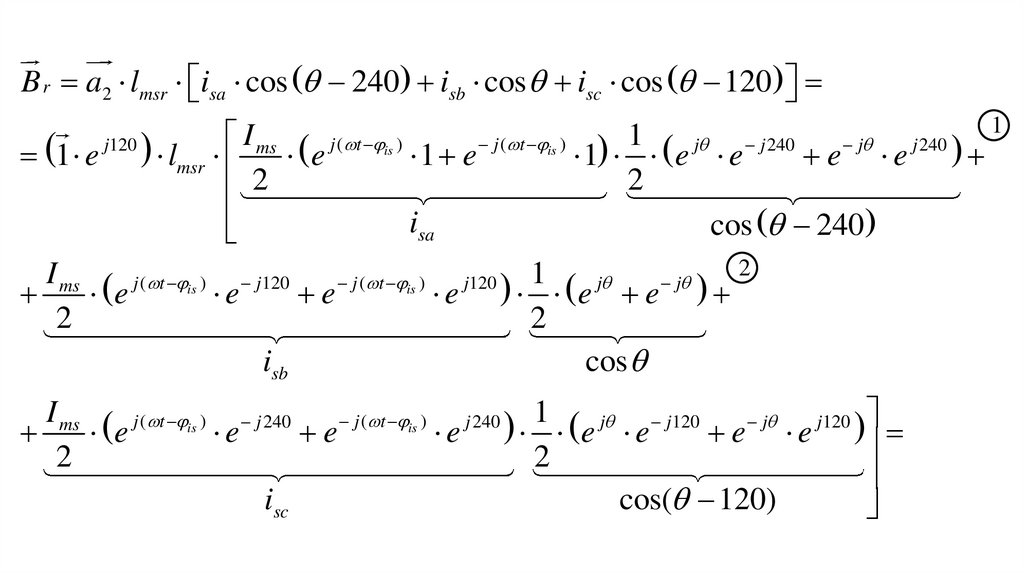

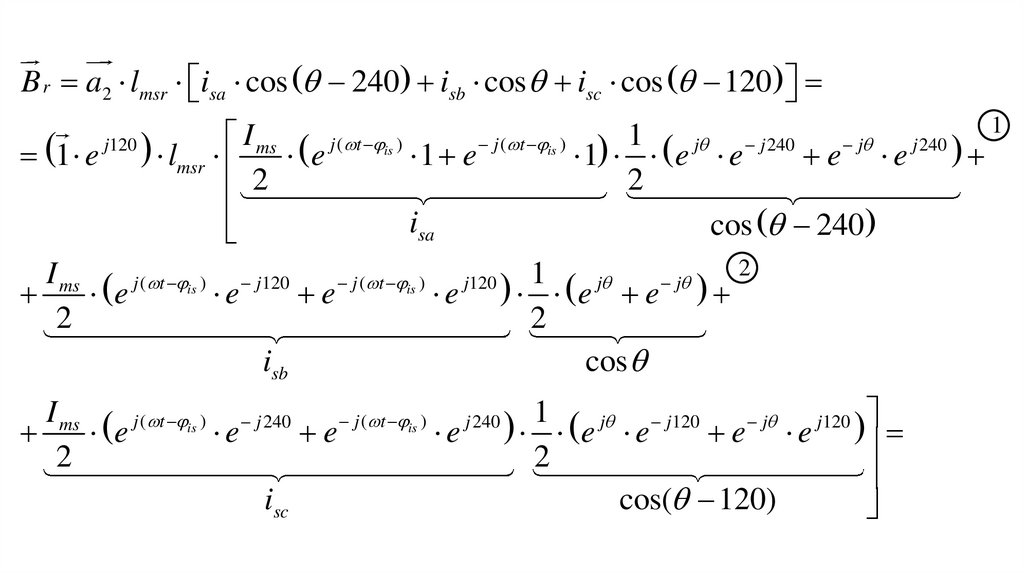


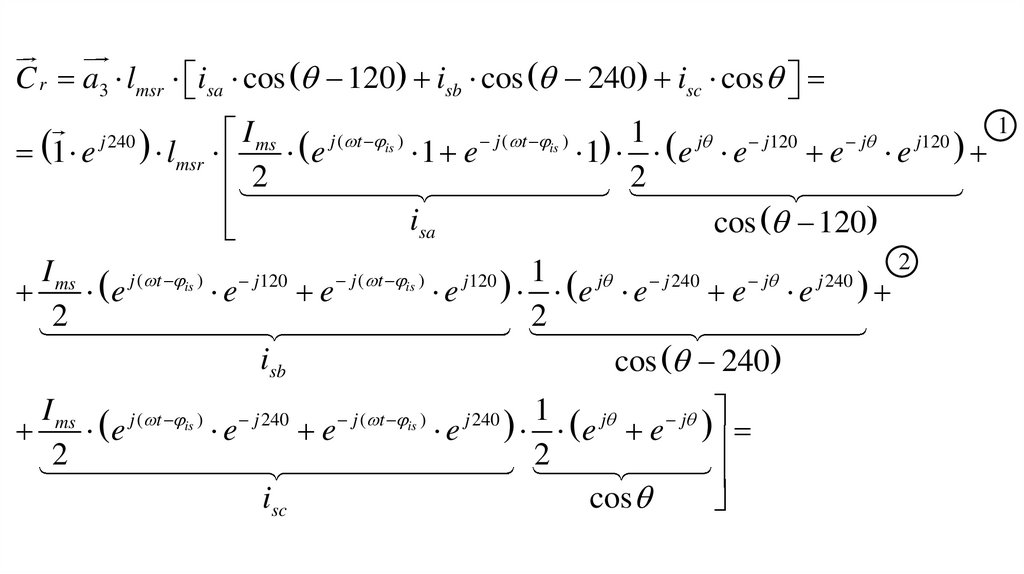
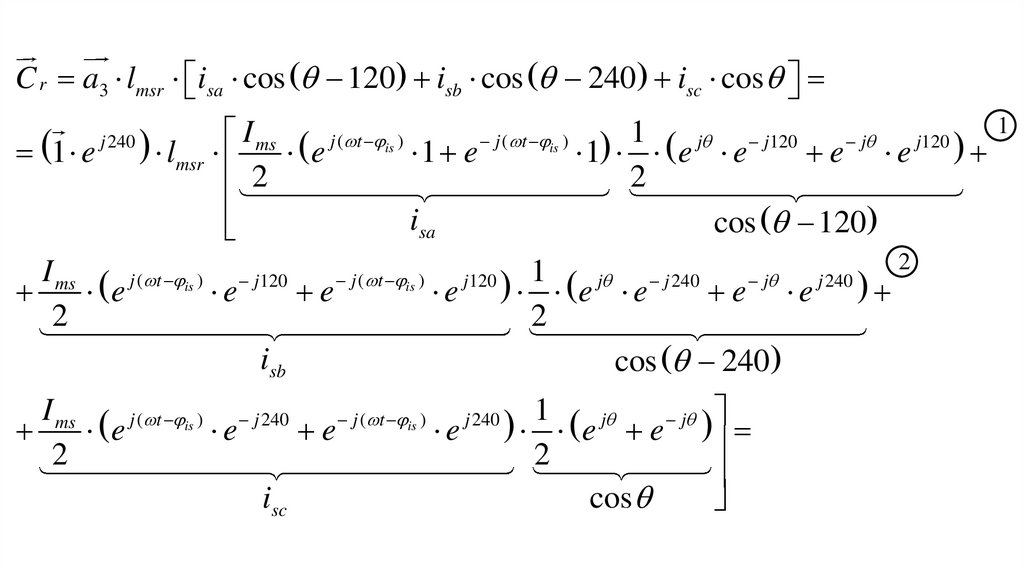
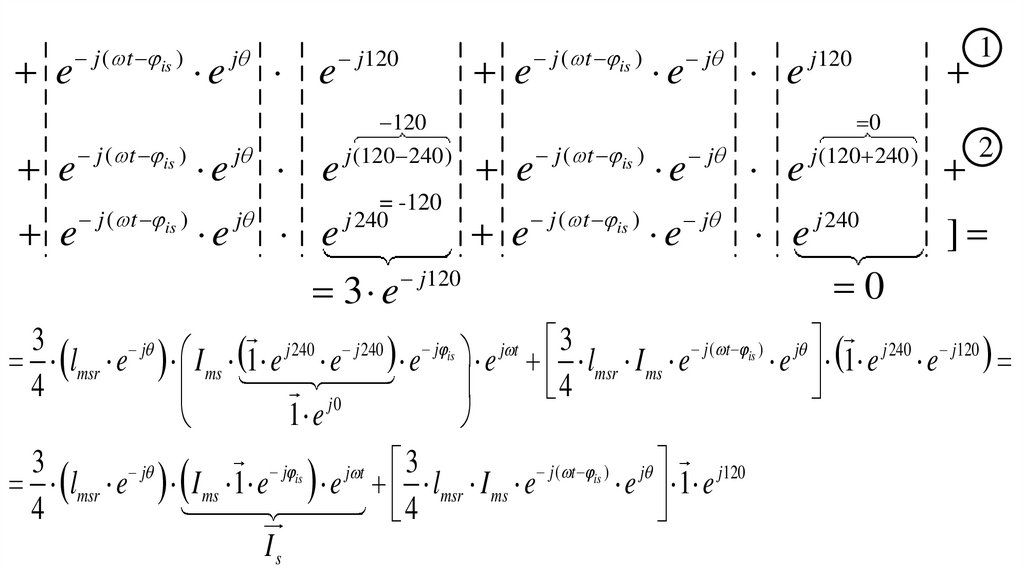
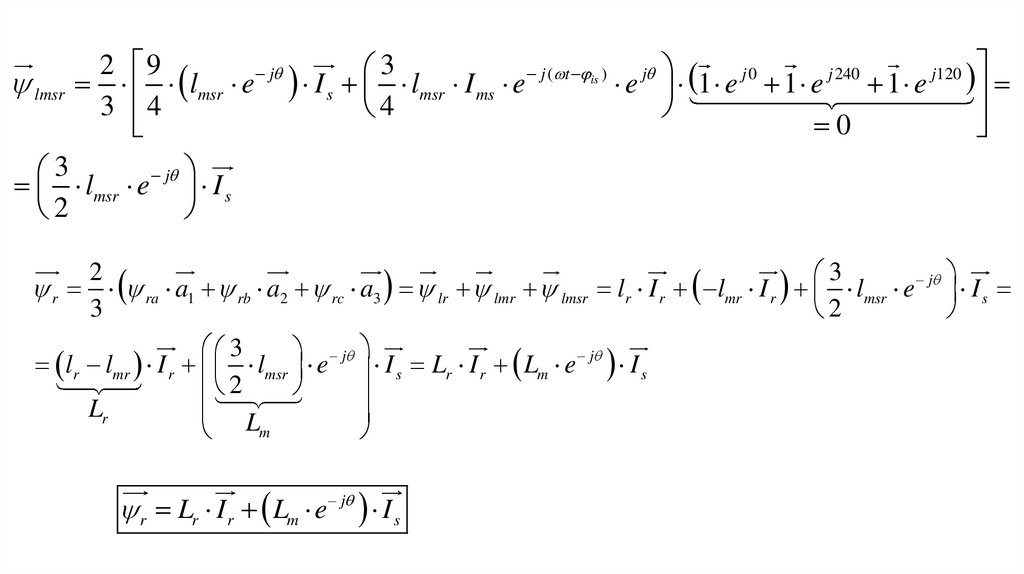
 Физика
Физика








