Дифференциальные уравнения с разделяющимися переменными

1.

www.themegallery.com
ДУ с разделяющимися переменными
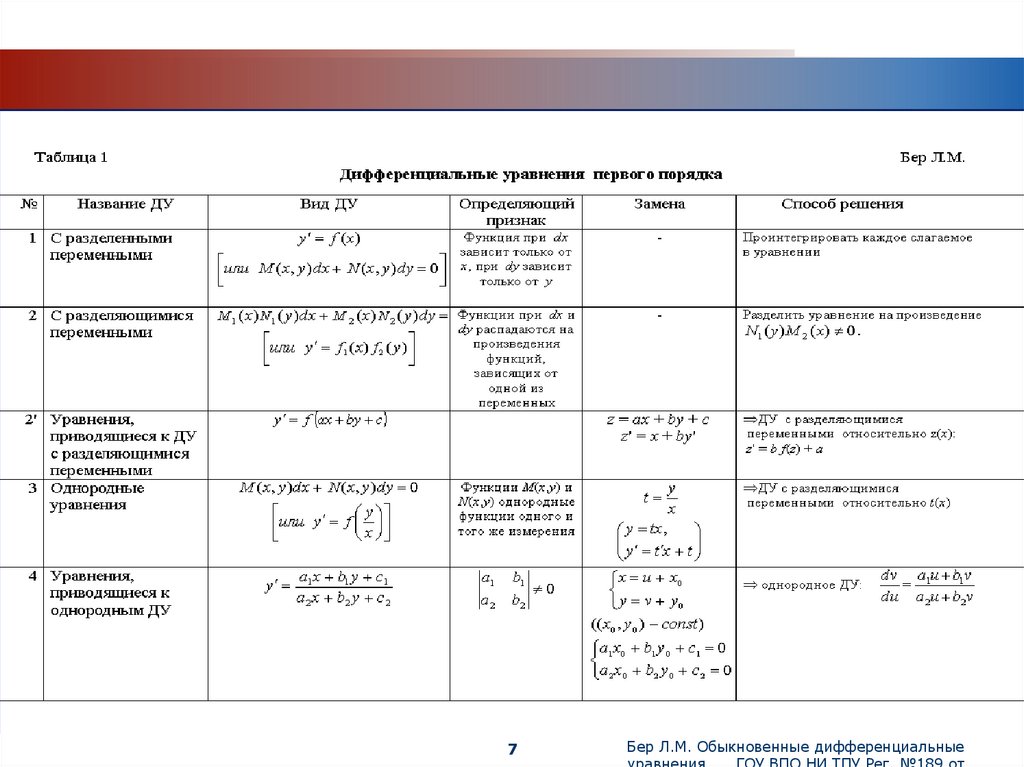
1. ДУ с разделенными переменными.
y' = f( x)
или
f (x) d x + (y) d y = 0
y
f ( x)dx C
( y)dy f ( x)dx C
2. ДУ с разделяющимися переменными.
М1 (x) N1(y) d x + М2 (x) N2(y) d y = 0 Разделить на N1(y) М2 (x) 0
Общий интеграл:
M 1 ( x)
N 2 ( y)
dx
M 2 ( x) N1 ( y) dy C
2 '. ДУ приводящееся к ДУ с разделяющимися переменными.
y' = f( ax + by + c)
Замена : z = ax + by + c z ' = b f (z) + a
Общий интеграл:
dz
x C
bf ( z ) a
1
Бер Л.М. Обыкновенные дифференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. №189 от

2.

www.themegallery.com
Однородные ДУ
Определение. Функция M (x, y) называется однородной измерения
(степени) m, если при любом t справедливо равенство
M (t x, t y) = t m · M (x, y).
Определение. Уравнение I-го порядка y' = f (x, y) называется
однородным относительно x и y, если функция f (x, y) есть однородная
функция нулевого измерения.
Определение. ДУ
М (x, y) d x + N (x, y) d y = 0
является однородным относительно x и y, если функции M (x, y) и N (x, y)
- однородные функции одного и того же измерения.
2
Бер Л.М. Обыкновенные дифференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. №189 от

3.

www.themegallery.com
Таблица
3. Однородные ДУ.
М (x, y) d x + N (x, y) d y = 0 Замена : y = t x, y' = t' x + t
или y' = f (y / x ) Замена : t = y / x
4. ДУ приводящееся к однородным.
y
a1 x b1 y c1
a2 x b2 y c2
Замена :
x u x0
y v y0
, если
a1
b1
a2
b2
a1 x0 b1 y0 c1 0
a2 x0 b2 y0 c2 0
(( x , y ) const ) :
0
0
0
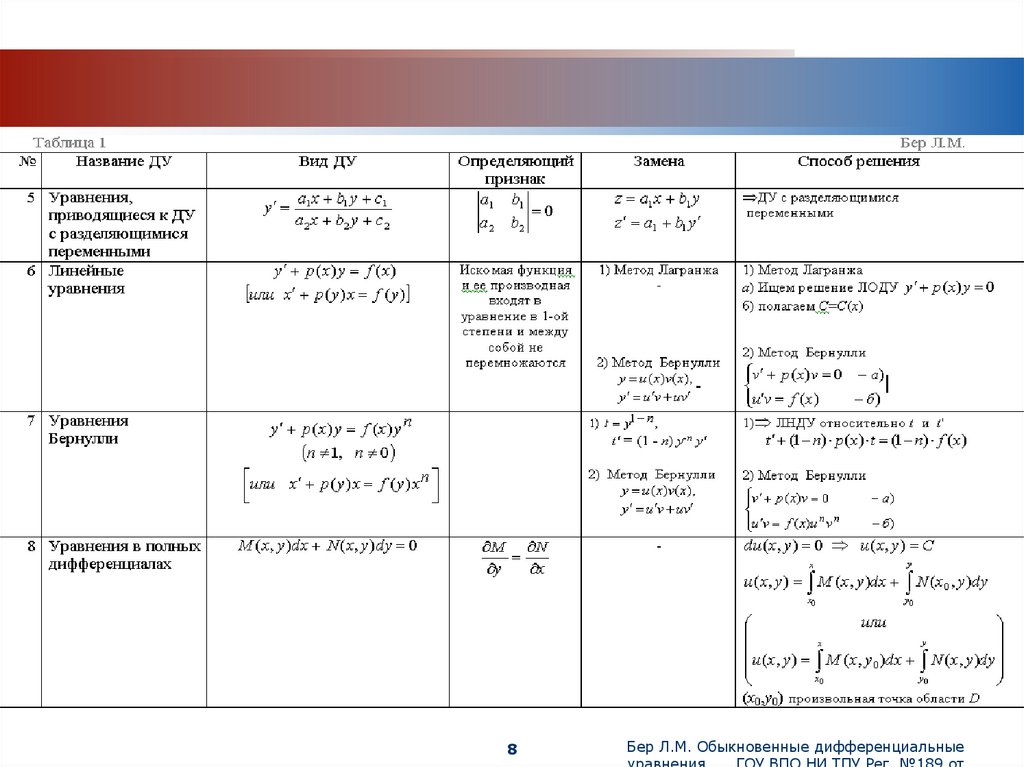
5. ДУ приводящееся к ДУ с разделяющимися переменными.
a1 x b1 y c1
y
a2 x b2 y c2
Замена : z = a1 x + b1 y
, если
a1
b1
a2
b2
0
z ' = a1 + b1 y '
3
Бер Л.М. Обыкновенные дифференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. №189 от

4.

www.themegallery.com
Линейные ДУ первого порядка
Определение. ДУ первого порядка, линейное относительно неизвестной
функции и ее производной называется линейным ДУ первого порядка.
В общем случае м.б. записано в виде:
y' + p (x) y = f( x).
Если f (x) = 0, то линейное ДУ называется однородным линейным ДУ.
Если f (x) 0, то линейное ДУ называется неоднородным линейным ДУ.
6. Линейные ДУ.
1) Метод Лагранжа (метод вариации постоянной)
а) Ищем решение ЛОДУ.
б) Полагаем С = С(x).
2) Метод Бернулли (подстановки)
Замена :
y u ( x)v( x),
Решаем систему
y u v uv
4
v p( x)v 0
u v f ( x)
а)
б)
Бер Л.М. Обыкновенные дифференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. №189 от

5.

www.themegallery.com
ДУ с разделяющимися переменными
7. Уравнения Бернулли.
1 способ Замена : t = y1-n , t' = (1 - n) y-n y'
y' + p (x) y = f( x) yn
2 способ Метод Бернулли
Замена :
y u ( x)v( x),
y u v uv
Решаем систему
v p( x)v 0
n n
u v f ( x)u v
а)
б)
8. ДУ в полных дифференциалах
М (x, y) d x + N (x, y) d y = 0
5
Бер Л.М. Обыкновенные дифференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. №189 от

6.

www.themegallery.com
ДУ в полных дифференциалах
Теорема. (о существовании и единственности решения ДУ в полных
дифференциалах) Пусть функции М (x, y) и N (x, y) определены и
непрерывны в области D плоскости Oxy и имеют в ней непрерывные
частные производные M / y и N / x . Для того, чтобы выражение
М (x, y) d x + N (x, y) d y
представляло собой полный дифференциал некоторой функции u (x, y)
необходимо и достаточно, чтобы во всех точках области D выполнялось
условие
M N
y
При этом
x
функция u (x, y) может быть найдена по одной из
следующих формул, (x0, y0) – любая точка области D
x
y
x
y
x0
y0
x0
y0
u ( x, y) M ( x, y)dx N ( x0 , y )dy или u ( x, y) M ( x, y0 )dx N ( x, y)dy
6
Бер Л.М. Обыкновенные дифференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. №189 от

7.

www.themegallery.com
7
Бер Л.М. Обыкновенные дифференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. №189 от

8.

www.themegallery.com
8
Бер Л.М. Обыкновенные дифференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. №189 от

9.

www.themegallery.com
Частные случаи ДУ F (x, y, y')=0
1. ДУ вида
y n p1 y n 1 ... pn 1 y pn y 0,
где pi = pi (x, y), n N называется ДУ первого порядка степени n.
Если удается разрешить относительно y ' (полагая y' = t), то
y' = f1(x, y, C), y' = f2(x, y, C),…, y' = fk(x, y, C) (k n).
Для каждого из уравнений найдем общий интеграл:
Ф1 (x, y, C) = 0, Ф2 (x, y, C) = 0, …, Фk (x, y, C) = 0
Общий интеграл ДУ записывается в виде:
Ф1 (x, y, C) · Ф2 (x, y, C) · … · Фk (x, y, C) = 0
2. ДУ не содержит явно x и y
F (y') = 0.
y C
Общий интеграл ДУ записывается в виде: F
0
9
x
Бер Л.М. Обыкновенные дифференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. №189 от

10.

www.themegallery.com
Частные случаи ДУ F (x, y, y')=0
3. ДУ не содержит явно искомой функции y
F (x, y') = 0.
x (t ),
y (t )
Общее решение в параметрическом виде:
Замена :
x (t ),
y (t ) (t )dt C.
4. ДУ не содержит x
F (y, y') = 0.
Замена :
y (t ),
y (t )
Общее решение в параметрическом виде:
10
(t )
x
dt C ,
(t )
y (t ).
Бер Л.М. Обыкновенные дифференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. №189 от

11.

www.themegallery.com
11
Бер Л.М. Обыкновенные дифференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. №189 от

12.

Спасибо за внимание
Бер Л.М. Обыкновенные дифференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. №189 от 17.06.10
12