Линейные однородные дифференциальные уравнения с постоянными коэффициентами

1.

www.themegallery.com
ЛОДУ с постоянными коэффициентами
Определение. Линейными однородными дифференциальными
уравнениями с постоянными коэффициентами называют уравнения вида
y(n) + p1 y(n-1) + …+ pn-1 y' + pn y = 0 ,
(6)
где коэффициенты p1 , p2 ,…, pn-1 , pn – const.
Частные решения будем искать в виде: y = ekx
(7)
Определение. Уравнение
kn + p1 k n-1 + …+ pn-1 k + pn = 0
(8)
называется характеристическим уравнением ЛОДУ с постоянными
коэффициентами, а многочлен
kn + p1 k n-1 + …+ pn-1 k + pn –
характеристическим многочленом.
1
Бер Л.М. Обыкновенные диференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. № 189 от

2.

www.themegallery.com
Алгоритм решения ЛОДУ n-го порядка с
постоянными коэффициентами
1. Составить характеристическое уравнение (y
=ekx).
2. Найти его корни k1, k2, …kn.
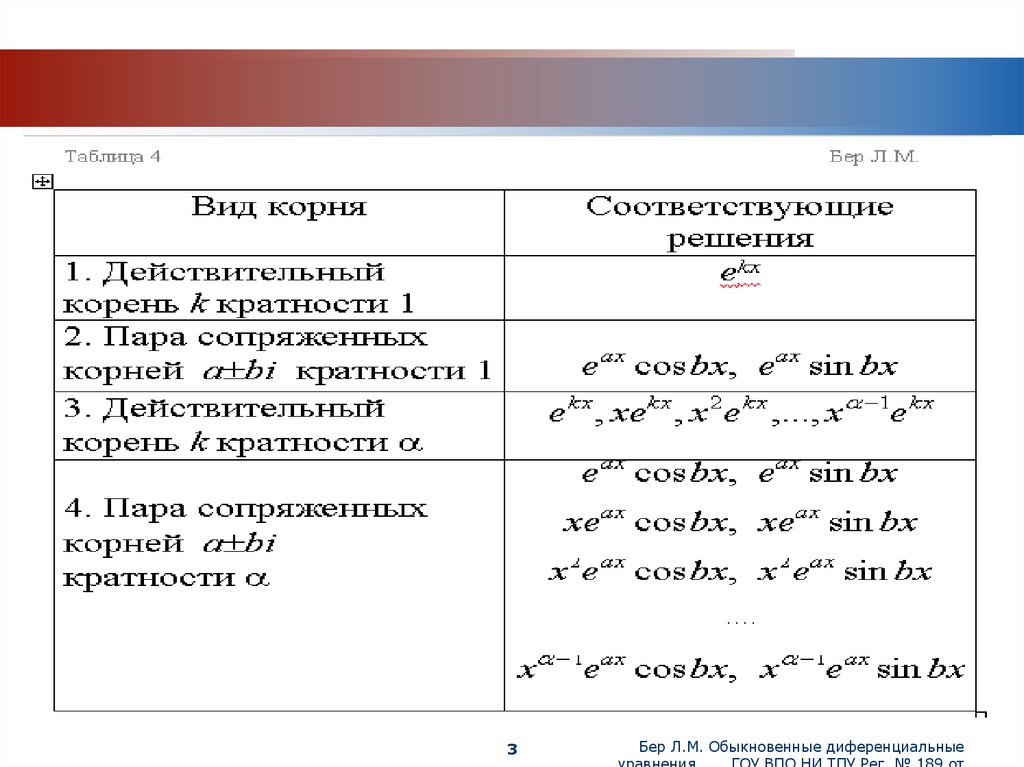
3. По характеру корней найти частные линейно
независимые решения y1(x), y2(x),… ,yn(x) согласно
таблице 4.
4. Записать общее решение
y(x) = C1 y1(x) + C2 y2(x) +…+ Cn yn (x).
2
Бер Л.М. Обыкновенные диференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. № 189 от

3.

www.themegallery.com
3
Бер Л.М. Обыкновенные диференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. № 189 от

4.

www.themegallery.com
ЛНДУ с произвольными коэффициентами
Вспомним, что ЛНДУ имеет вид
y(n) + p1(x) y(n-1) + …+ pn-1(x) y' + pn(x) y = f(x),
(9)
где p1 (x), p2(x), …, pn (x), f(x) – заданные функции аргумента x,
причем f(x) 0 .
Теорема 4. (О структуре общего решения ЛНДУ)
Общее решение ЛНДУ есть сумма его частного решения и
общего решения соответствующего однородного уравнения.
При n = 2, ЛНДУ 2-го порядка
y'' + p1(x) y' + p2(x) y = f(x).
4
(9')
Бер Л.М. Обыкновенные диференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. № 189 от

5.

www.themegallery.com
ЛНДУ с произвольными коэффициентами
Теорема 5. (Принцип суперпозиции решений)
Если функция y i (x) – является решением ЛНДУ
y (n) + p1(x) y(n-1) + …+ pn-1(x) y' + p n (x) y = f i (x),
то функция
y = 1 y1 + 2 y2 +…+ k yk
(11)
является решением уравнения
y(n) + p1(x) y(n-1) + …+ pn(x) y = 1 f1 (x) + 2 f2(x) +…+ k fk (x) .
(12)
При n = 2, ЛНДУ 2-го порядка
y'' + p1(x) y' + p2(x) y = 1 f1 (x) + 2 f2(x).
5
Бер Л.М. Обыкновенные диференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. № 189 от

6.

www.themegallery.com
ЛНДУ n-го порядка
Рассмотрим ЛНДУ с постоянными коэффициентами
y(n) + p1 y(n-1) + …+ pn-1 y' + pn y = f (x) ,
где коэффициенты p1 , p2 ,…, pn-1 , pn – const.
Метод
неопределенных
коэффициентов
применить, если правая часть имеет вид
можно
f (x) = e px [Pm (x) cos q x +Ql (x) sin q x],
где Pm (x) и Q l (x) – многочлены степени
соответственно, p и q – некоторые числа.
6
m и
Бер Л.М. Обыкновенные диференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. № 189 от
l

7.

www.themegallery.com
Форма частного решения
7
Бер Л.М. Обыкновенные диференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. № 189 от

8.

www.themegallery.com
ЛНДУ n-го порядка
Замечание 1. Степени многочленов Pm (x) и Q l (x) в
случаях 3,4 таблицы 5 можно считать одинаковой (max {m, l}).
В этом случае коэффициенты при недостающих степенях
одного из многочленов можно считать равными нулю.
Замечание 2. Правая часть уравнения может содержать
несколько слагаемых; в этом случае частное решение также
составляется из нескольких слагаемых в соответствии с
теоремой 5.
8
Бер Л.М. Обыкновенные диференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. № 189 от

9.

www.themegallery.com
Метод Лагранжа для ЛНДУ в п
Система линейных неоднородных уравнений с n
неизвестными функциями Ci (x), i = 1, 2, …, n:
С1 ( x) y1 C 2 ( x) y 2 ...C n ( x) y n 0
С1 ( x) y1 C 2 ( x) y 2 ...C n ( x) y n 0
...
С ( x) y ( n 2 ) C ( x) y ( n 2 ) ...C ( x) y ( n 2 ) 0
1
2
2
n
n
1
С1 ( x) y1( n 1) C 2 ( x) y 2( n 1) ...C n ( x) y n( n 1) f ( x)
9
(17)
Бер Л.М. Обыкновенные диференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. № 189 от

10.

www.themegallery.com
Алгоритм решения ЛНДУ n-го порядка
методом Лагранжа
1. Найти ФСР ЛОДУ соответствующего ЛНДУ и записать
его общее решение:
y (x) = C1 y1(x) + C2 y2(x) +…+ Cn yn (x).
2. Записать решение ЛНДУ в форме общего решения
ЛОДУ, считая C i = C i (x), i = 1, 2, …, n :
y (x) = C1 (x) y1 (x) + C2 (x) y2(x) +…+ Cn (x) yn (x).
(18)
3. Построить систему для определения C i' (x) и решить ее
согласно (17).
4. Найти Ci (x) и подставить их в общее решение ЛНДУ
(18).
10
Бер Л.М. Обыкновенные диференциальные
уравнения
ГОУ ВПО НИ ТПУ Рег. № 189 от

11.

Спасибо за внимание
Бер Л.М. Обыкновенные диференциальные уравнения
ГОУ ВПО НИ ТПУ Рег. № 189 от 17.06.10
11