Похожие презентации:
Аффинные системы координат
1. Тема 4. Аффинные системы координат
Задачи темы 4:• Познакомить
Ввести понятиечитателя
аффинного
(точечного) пространства
с операциями
векторного ии
аффинных систем
координат (в
частности, ДПСК).
смешанного
произведения
геометрических
векторов,
свойствами
операций
и основными фиксированной
направлениями
• Установитьэтих
связь
между координатами
использования.
точки в различных аффинных системах координат.
• Привести
основные и виды
уравнений
линии на
Обсудить свойства
возможности
использования
плоскости
аффинной системе
координат.
операции вскалярного
произведения
геометрических
векторов.
• Распространить операцию скалярного произведения, а
также такие понятия, как длина вектора (норма) и
расстояние между точками на случай вещественного
n-мерного пространства.
2.
§4.1. Связь между векторным и точечнымпространством. Декартова прямоугольная система
координат
Сущность метода координат заключается в том, что
различным геометрическим объектам сопоставляются
некоторым стандартным способом уравнения или
системы уравнений, а изучение свойств геометрических
объектов сводится к изучению свойств уравнений.
Под аффинным пространством
мы будем понимать множество точек, для которого
заданы:
• линейное пространство W (ассоциированное с );
• соответствие, сопоставляющее любым двум точкам
A, B определенный вектор AB W;
причем выполнены аксиомы:
3.
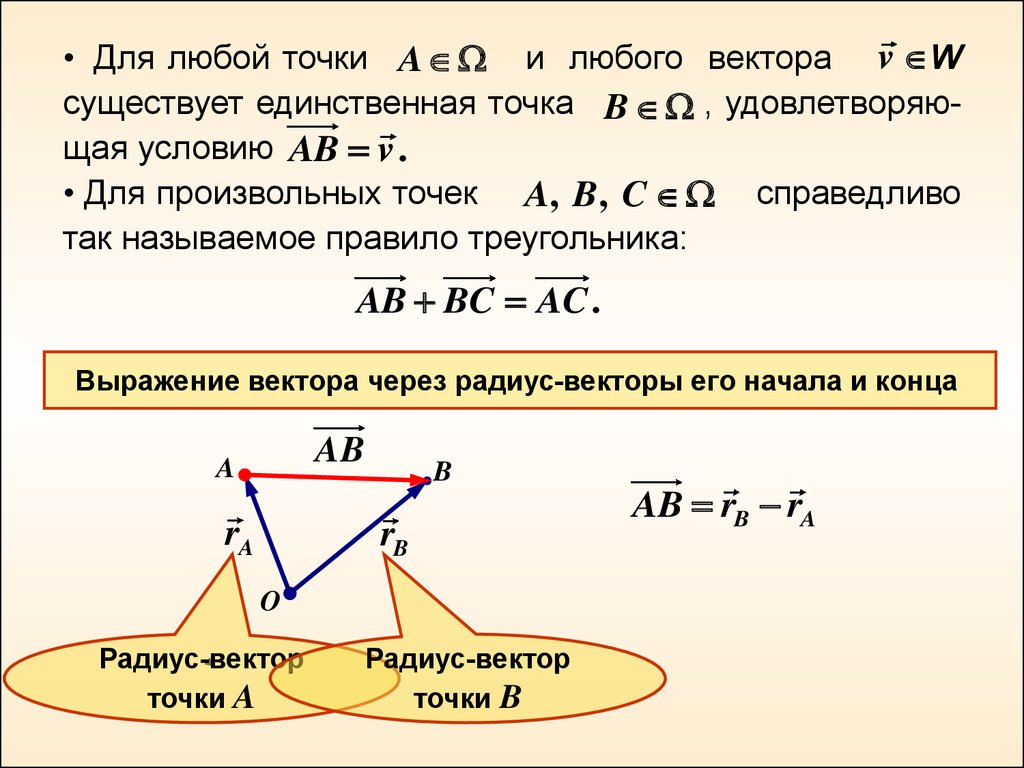
• Для любой точки A и любого вектора v Wсуществует единственная точка B , удовлетворяющая условию AB v .
• Для произвольных точек A, B, C справедливо
так называемое правило треугольника:
AB BC AC .
Выражение вектора через радиус-векторы его начала и конца
AB
A
rA
B
rB
O
Радиус-вектор
точки A
Радиус-вектор
точки B
AB rB rA
4.
Аффинной системой координат ваффинном пространстве 2 , называют совокупность,
состоящую из:
• фиксированной точки O 2 (начала координат);
• базиса {v1 , v2 } соответствующего (ассоциированного с
2) линейного пространства V 2 .
C ( x1 , x2 )
OC rC x1v1 x2v2
OC ( x1 , x2 )
AB ( x1B x1A )v1 ( x2B x2A )v2
B
A
B
A
AB
(
x
x
,
x
x
или
1
1
2
2 )
Координаты вектора
AB
5.
2V
R
2
2
• Ортонормированный базис;
• Декартова
(ДПСК)
прямоугольная
система
координат
6.
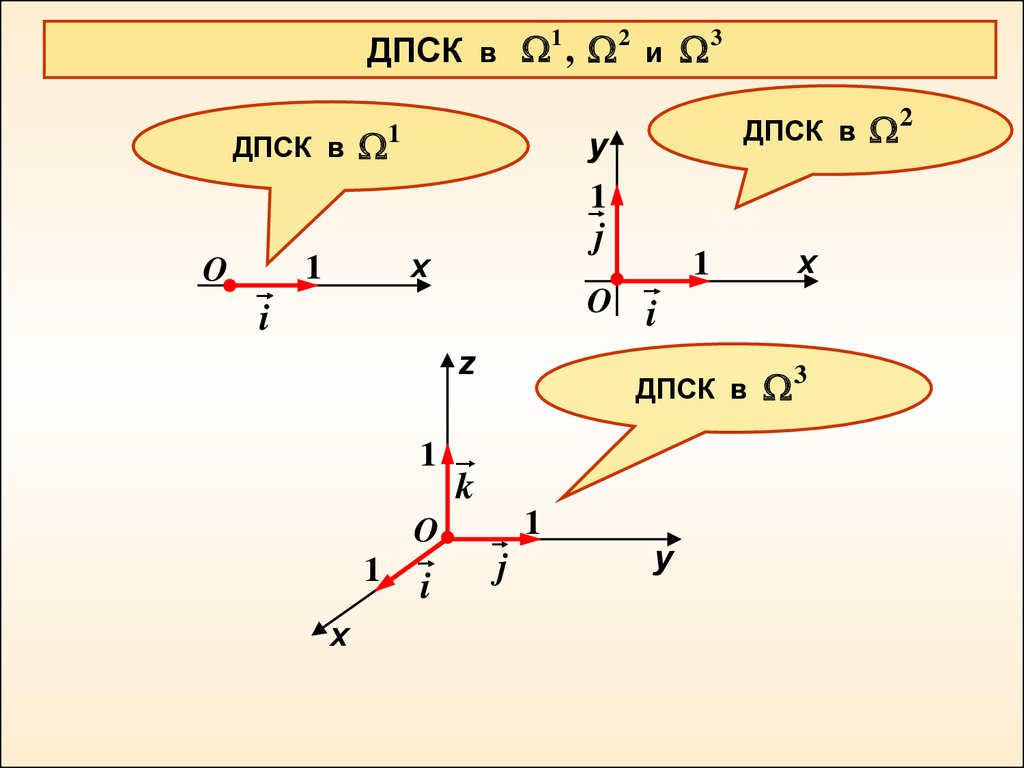
1ДПСК в , 2 и 3
ДПСК в
j
O
i
z
1
x
i
1
k
1
j
x
i
ДПСК в
O
1
ДПСК в
y
1
x
1
O
1
y
3
2
7.
§4.2. Связь между координатами точки в различныхаффинных системах координат
Две аффинные системы координат
M
rM
v2
O
rM
v2
O
v1
v1
rM OM xv1 yv2
O M x v1 y v2
rM
8.
v1 t11v1 t12v2 ,v2 t21v1 t22v2 ,
OO pv1 qv2 .
t11
T
t 21
t12
t 22
Матрица перехода от базиса
rM xv1 yv2
v1 , v2 к базису v1 , v2
rM OO rM
pv1 qv2 x t11v1 t12v2 y t 21v1 t 22v2
9.
x p t11 x t 21 yy q t12 x t 22 y
Координаты точки M
в первой системе
координат
Координаты точки M
во второй системе
координат
Координаты фиксированной точки
аффинного пространства в одной аффинной системе
координат являются линейными функциями координат
той же точки в другой аффинной системе координат.
Обратно
10.
§4.3. Скалярное произведение геометрическихвекторов в ДПСК
a
b
(a , b) a .b a b cos
Свойства скалярного произведения
(a , b) (b, a ).
(a , b) ( a , b) R1 .
(a b, c ) (a , c ) (b, c ).
(b, b) 0; (b, b) 0 b 0.
11.
a .b (a1 i a2 j ) (b1 i b2 j )a1b1 (i , i ) a2b2 ( j , j ) (a1b2 a2b1 )(i , j ) a1b1 a2b2 .
Выражения для угла между ненулевыми векторами,
длины вектора и для орта произвольного ненулевого
вектора a в ДПСК:
arccos
(a , b)
a12 a22 b12 b22
a a12 a22
ea
1
a12 a22
a
12.
Необходимое и достаточное условиеперпендикулярности ненулевых векторов a и b
a1b1 a2b2 0
Расстояние между точками A( x A , y A ) и B( xB , yB )
( A, B ) AB ( xB x A ) ( yB y A )
2
2
13.
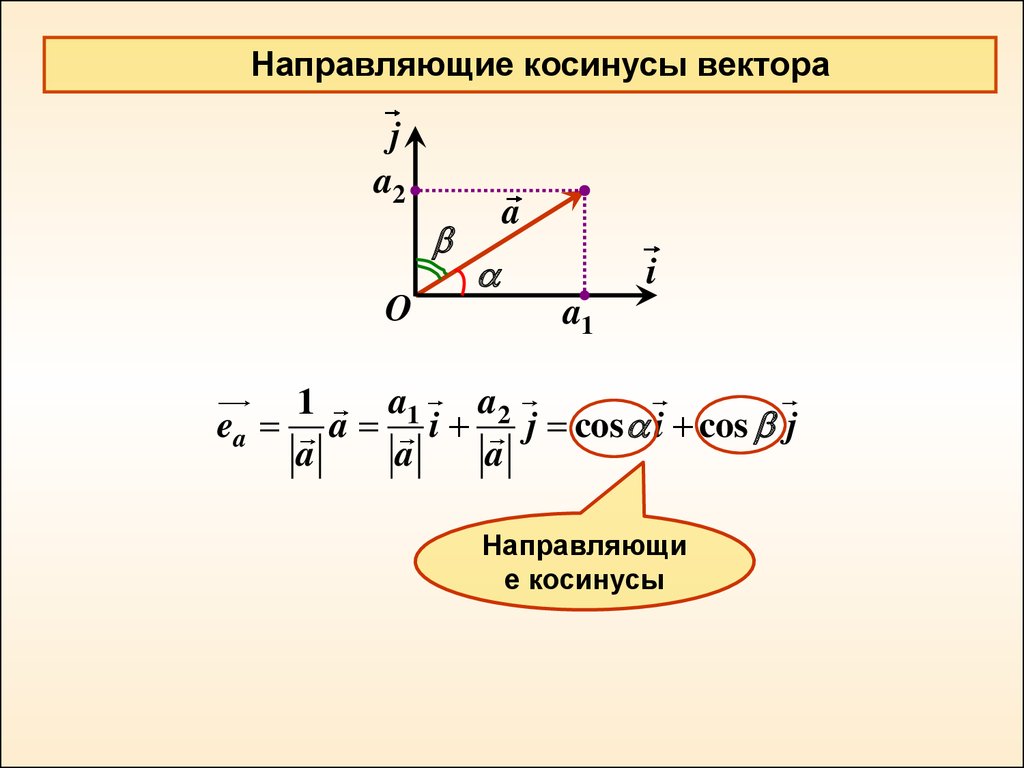
Направляющие косинусы вектораj
a2
O
a
i
a1
a1
a2
1
ea a i
j cos i cos j
a
a
a
Направляющи
е косинусы
14.
§4.4. Скалярное произведение, норма и расстояниев n-мерном пространстве
a (a1 ,
, an ), b (b1 ,
a .b (a , b) a1b1 a2b2
, bn ) R n
anbn
Домашнее задание
аналоги выражений
для угла между
ненулевыми
• понятие
нормированного
и
метрического
•пространства.
неравенство Коши-Буняковского;
векторами,
длины
вектора
и
для
орта
произвольного ненулевого вектора;
15.
§4.5. Представление о векторном и смешанномпроизведении геометрических векторов
Векторное произведение (вектора a на вектор b)
a b c :
• модуль вектора c равен произведению
векторов a и b на синус угла между ними:
модулей
c a b sin ;
• вектор c перпендикулярен вектору a и вектору b ;
• тройка векторов a , b и c является правой:
c
b
a
16.
Свойства векторного произведенияa b 0
векторы a и b коллинеарны.
a b (b a ).
(a b) ( a ) b R1 .
(a b) c a c b c .
a a 0.
17.
Пусть ( xa , ya , za ) и ( xb , yb , zb ) – координаты векторов a и b соответственно в ортонормированном базисе ( i , j , k ) пространства V 3. Тогда координатывектора a b в том же базисе могут быть найдены по
формуле:
i
a b xa
xb
j
ya
yb
k
ya
za
yb
zb
za
zb
i
xa
za
xb
zb
j
xa
ya
xb
yb
k
18.
Применение операции векторного произведениявекторов
• Определение множества векторов, перпендикулярных
двум неколлинеарным векторам a и b .
• Поиск площади треугольника и параллелограмма.
Домашнее задание
При какомсмешанного
условии
вектор
попадает
в меньший
с трех
• Свойства
Смешанное
произведение
геометрических
произведения
векторов
угол, образованный векторами a и b ?
векторов
b
c
a
19.
§4.6. Задание линий на плоскости с помощьюуравнений
2
–
аффинная
система
координат
на
плоскости
R
Ov1v 2
r rM OM xv1 yv 2
2
Уравнение линии L на плоскости R
M ( x, y)
относительно заданной аффинной системы
координат:
F ( x , y ) 0,
где F – совокупность некоторых операций над
вещественными числами x и y, причем выполнены два
условия:
• координаты x и y любой точки M ( x , y ) L удовлетворяют уравнению линии F ( x , y ) 0;
• любая пара чисел x и y, удовлетворяющих уравнению
линии, представляет собой координаты некоторой точки
M(x,y) на линии L.
20.
Параметрические уравнения линии L2
на плоскости R относительно заданной аффинной системы координат:
x x(t )
, t T,
y y( t )
(*)
где t T R – вещественный параметр, причем:
2
• координаты x и y каждой точки M ( x , y ) L получаются из системы (*) при некотором значении параметра t T ;
• каждое значение параметра t T определяет посредством (*) координаты x(t) и y(t) некоторой точки M L.
21.
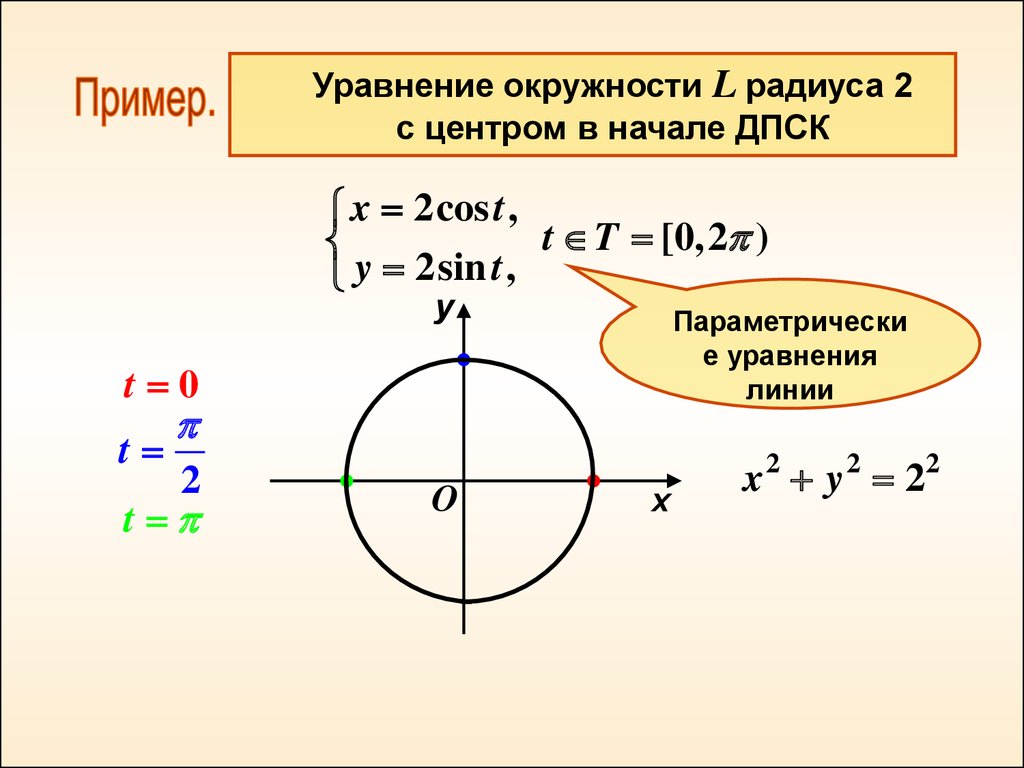
Уравнение окружности L радиуса 2с центром в начале ДПСК
x 2cos t ,
t T [0,2 )
y 2sin t ,
y
Параметрически
е уравнения
линии
t 0
t
2
t
O
x
x 2 y 2 22
22.
• Как выбрать систему координат, в которойуравнение заданной линии выглядит наиболее
простым образом?
Естественная (каноническая) система
координат
23.
Примералгебраического
полинома
третьего
порядка относительно переменных x и y:
P3 ( x , y ) 2 x 2 y 5 xy 2 xy x 1
Алгебраическое уравнение n-го порядка
(относительно x и y)
F ( x , y ) Pn ( x , y ) 0
Если линия L на плоскости определяется в некоторой
ДПСК алгебраическим уравнением n-го порядка, то в
любой другой аффинной системе координат эта линия
будет определяться алгебраическим уравнением того же
порядка.
К свойству
24.
Линия L на плоскости (или поверхностьS в пространстве) называется алгебраической порядка n,
если в некоторой ДПСК эта линия (поверхность)
определяется алгебраическим уравнение n-го порядка.
25. Выводы
система произведениякоординат
наестественным
плоскости
• Аффинная
Операция скалярного
устанавливает
взаимно однозначные
соответствия
образом распространяется
на случай пространства
Rn ,
2
n
между
множеством
плоскости,
.
что позволяет2 определить всех
нормуточек
и расстояние
в R множеством V
их
радиус-векторов
и множест• Операция
векторного
произведения
позволяет
описать
2
вом
точек.
R наборов
множество
всех координат
векторов,этих
перпендикулярных
двум
• заданным
Координаты
фиксированной
точки
аффинного
неколлинеарным
векторам,
а также
находить
пространства
в одной аффинной
системе координат
площади
треугольников
и параллелограммов.
функциями
координат
той же
• являются
Если линиялинейными
L на плоскости
определяется
в некоторой
точки в другой аффинной системе координат.
ДПСК алгебраическим уравнением n-го порядка, то в
• Операция
скалярного
геометрических
любой другой
аффиннойпроизведения
системе координат
эта линия
векторов
позволяет находить
угол между
векторами,
будет определяться
алгебраическим
уравнением
того2
длину
вектора, а также расстояние между точками в R
же порядка.
3
и R .




















 Математика
Математика








