Метод координат на плоскости

1.

Добрый день!!!
Задание на 24.11.2020.
Изучите теорию,
выполните задания.

2.

3.

Лемма о коллинеарных векторах
Лемма
Если векторы а и b коллинеарны и а ≠ 0,
то существует такое число k, что b = ka
Доказательство:
1 случай: a↑↑b.
Пусть k =
│b│
b
a
kа
. Т.к. k ≥ 0,
│a│
то векторы ka и b сонаправлены.
Их длины равны: │ka│= │k│∙│a│=
Поэтому b = ka.
│b│
│a│
∙│a│=│b│.

4.

Лемма о коллинеарных векторах
Доказательство:
b
a
2 случай: a↑↓b.
Пусть k = –
│b│
kа
. Т.к. k < 0,
│a│
то векторы ka и b сонаправлены.
Их длины равны: │ka│= │k│∙│a│=
Поэтому b = ka.
Чтд.
│b│
│a│
∙│a│=│b│.

5.

Разложение вектора по двум
неколлинеарным векторам
Пусть а и b – два данных вектора. Если вектор р
представлен в виде р = ха + уb, где х и у – некоторые
числа, то говорят, что вектор р разложен по
векторам а и b.
Числа х и у называют коэффициентами разложения.

6.

Разложение вектора по двум
неколлинеарным векторам
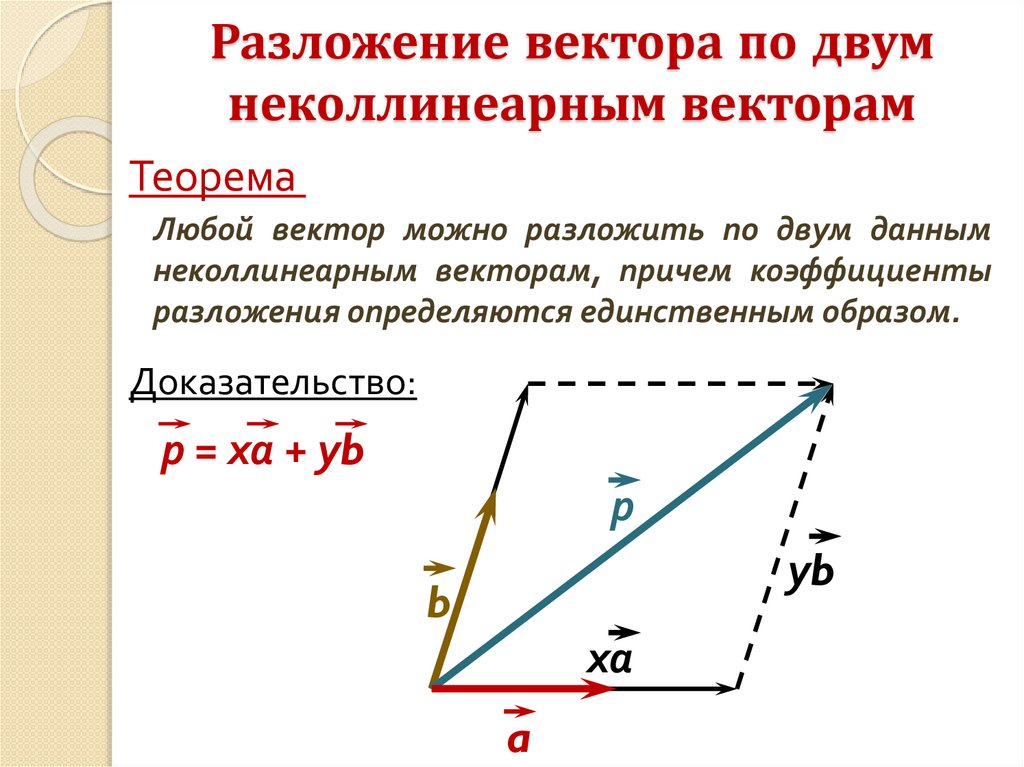
Теорема
Любой вектор можно разложить по двум данным
неколлинеарным векторам, причем коэффициенты
разложения определяются единственным образом.
Доказательство:
р = ха + уb
р
уb
b
ха
a

7.

Разобрать решение №911(а,б),
в тетрадке выполнить №911(в,г)

8.

Разобрать решение №912(а-г),
в тетрадке выполнить №912(д-и)

9.

Изучите тему «Координаты вектора»
посмотрев видео
и выполните задания:
№919,
№920,
№922(а,б),
№923(а,б),
№924

10.

Выполните самостоятельную работу по вариантам, оформив следующим
образом:
Самостоятельная работа по теме «Координаты вектора», выполненная
учеником 9 класса _____ Ф.И.
Вариант №_____

11.

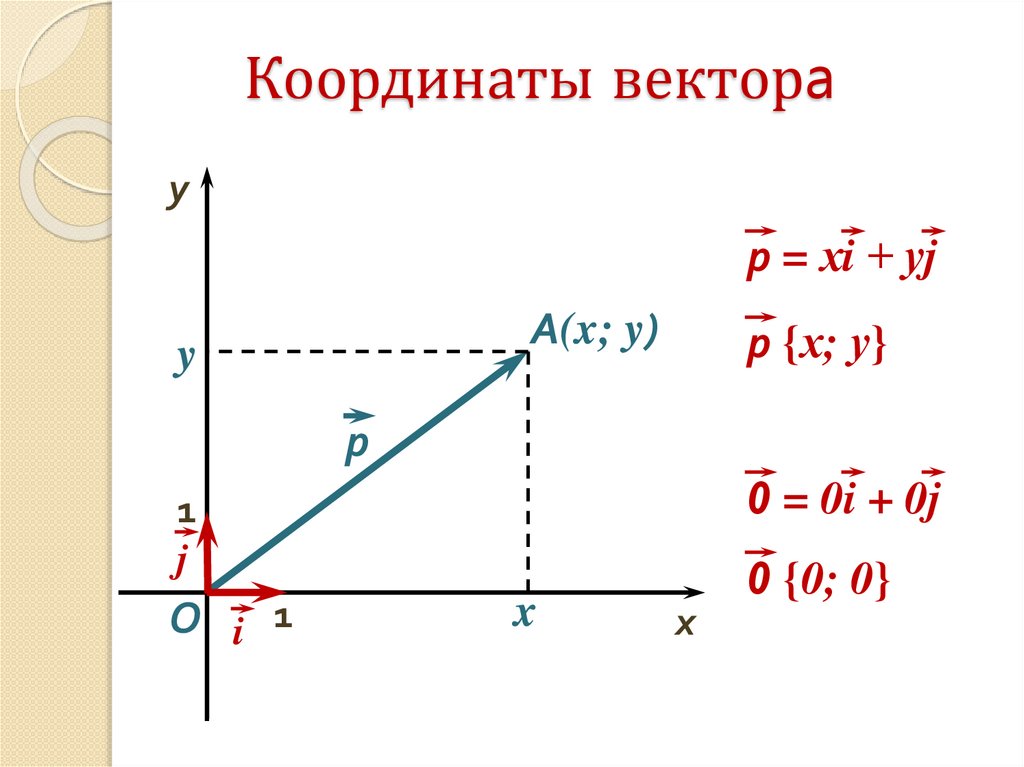
Координаты векторa
y
р = хi + уj
A(x; y)
y
р {х; у}
р
0 = 0i + 0j
1
j
O i 1
x
0 {0; 0}
x

12.

Действия над векторами
а {х1; у1}
b {х2; у2}
1. Каждая координата суммы двух или более
векторов равна сумме соответствующих
координат этих векторов.
а + b { х1 + x2; у1 + y2 }
2. Каждая координата разности двух векторов
равна разности соответствующих
координат этих векторов.
а – b { х1 – x2; у1 – y2 }

13.

Действия над векторами
а {х1; у1}
3. Каждая координата произведения вектора на
число равна произведению соответствующей
координаты вектора на это число.
kа { kх1; kу1 }