Молекулярно-кинетический подход применительно к расчету тепловой нагрузки при пленочном кипении

1.

Молекулярно-кинетический подход
применительно к расчету тепловой
нагрузки при пленочном кипении на
сферических и цилиндрических
греющих поверхностях

2.

Кипение воды на полусферической поверхности
dw = 1.0 см; Tw = 270o C; Tb = 40o C
2

3.

Юрий Петрович Ивочкин
Константин Кубриков

4.

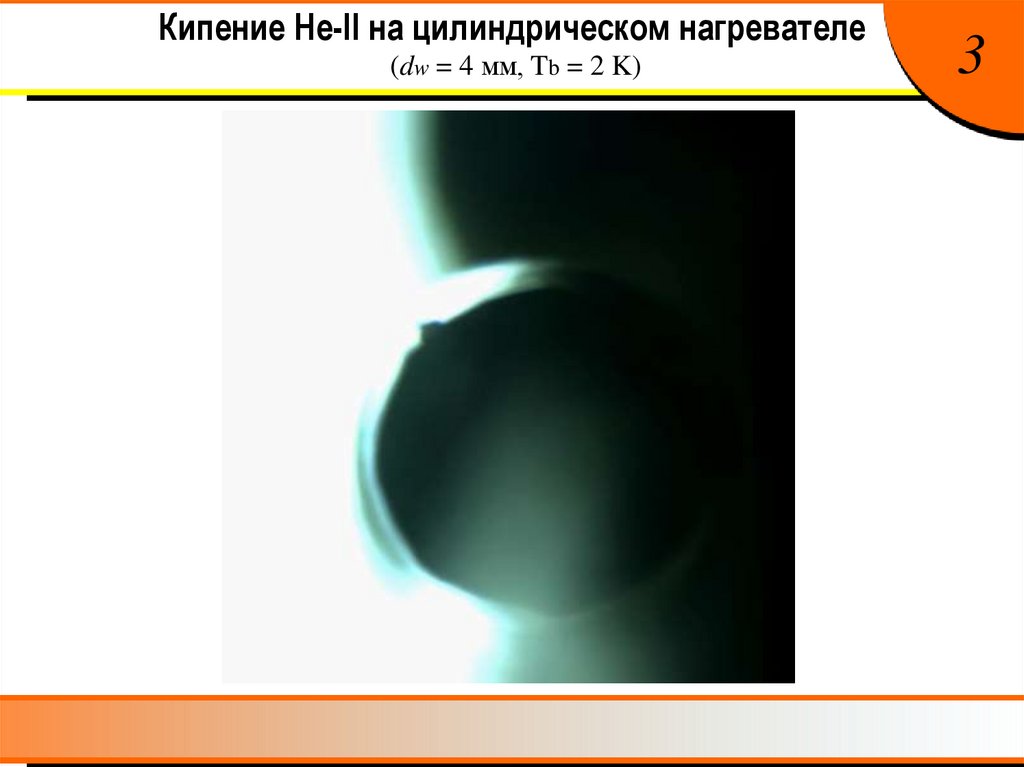
Кипение He-II на цилиндрическом нагревателе
(dw = 4 мм, Tb = 2 K)
3

5.

Пленочное кипение Не-II на цилиндре
4

6.

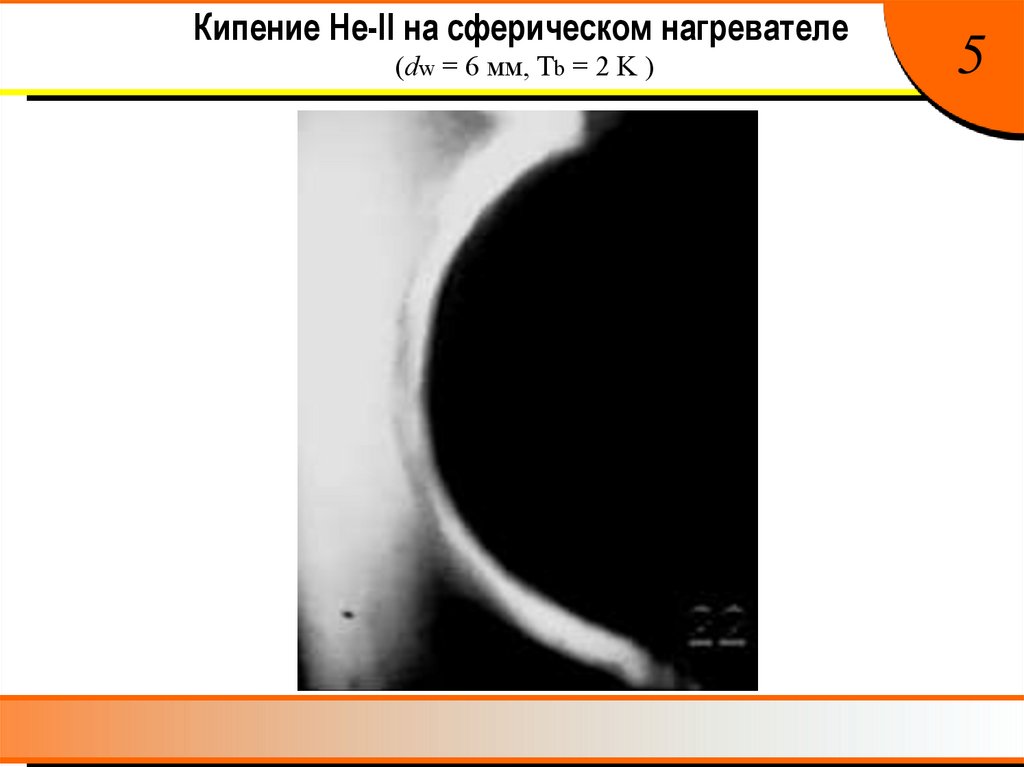
Кипение He-II на сферическом нагревателе
(dw = 6 мм, Tb = 2 K )
5

7.

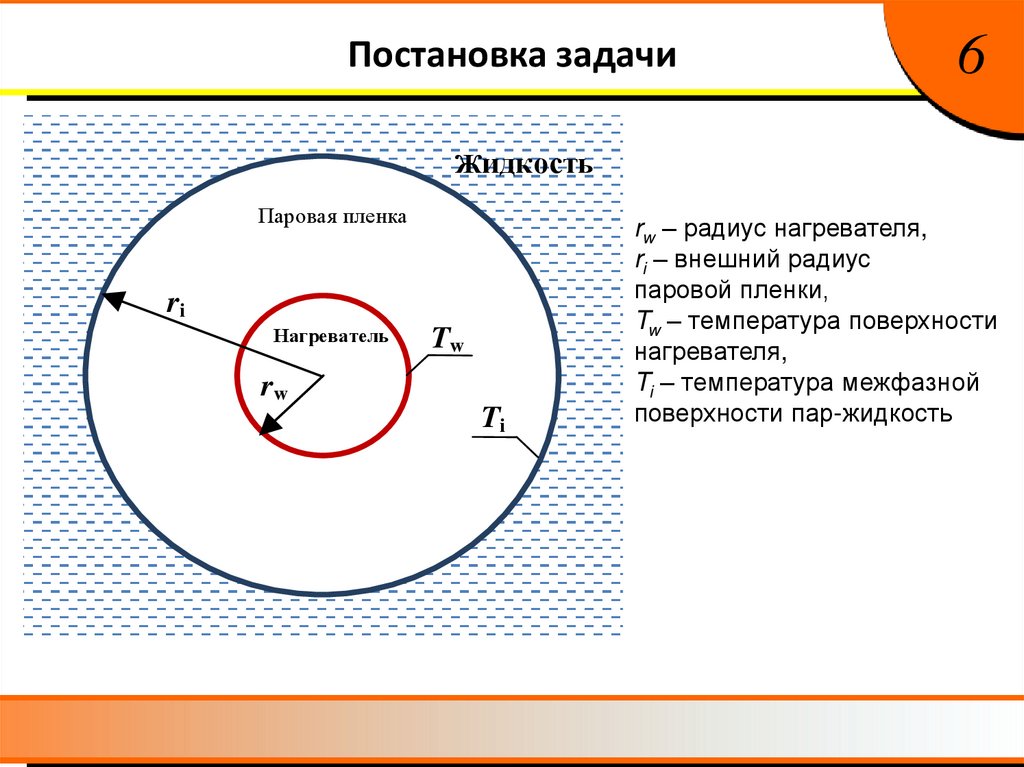
Постановка задачи
6
Жидкость
Паровая пленка
ri
Нагреватель
Tw
rw
Ti
rw – радиус нагревателя,
ri – внешний радиус
паровой пленки,
Tw – температура поверхности
нагревателя,
Ti – температура межфазной
поверхности пар-жидкость

8.

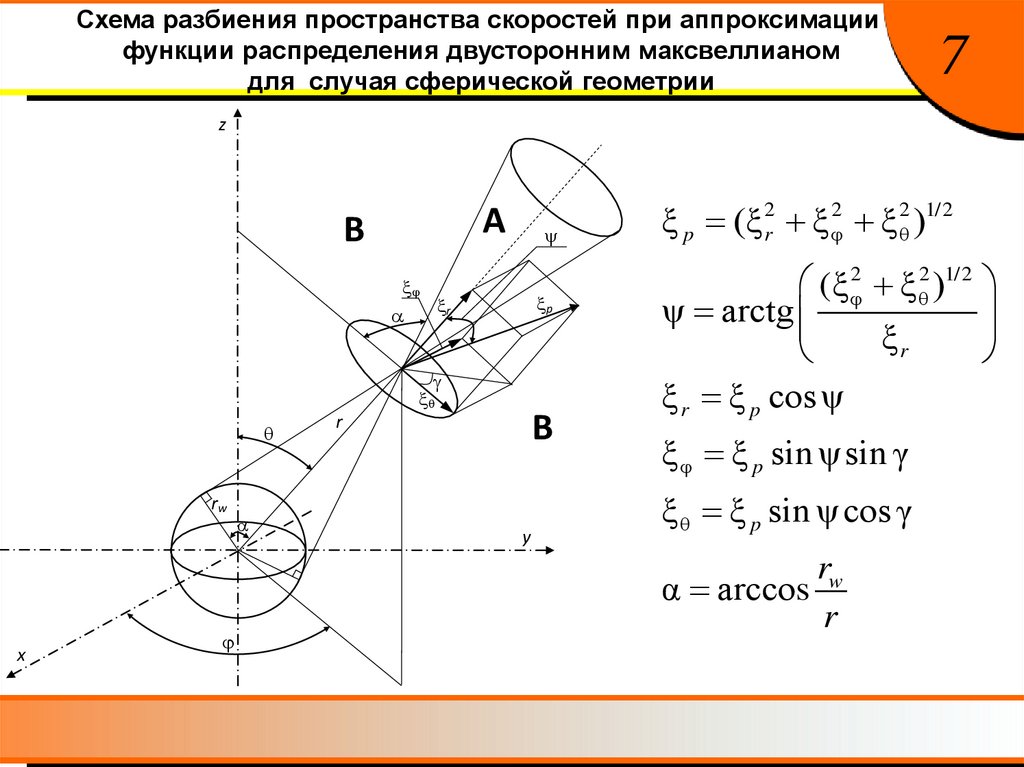
Схема разбиения пространства скоростей при аппроксимации
функции распределения двусторонним максвеллианом
для случая сферической геометрии
7
z
А
В
p
r
rw
x
В
r
y
ξ p (ξ r2 ξ φ2 ξ θ2 )1/2
(ξ φ2 ξ θ2 )1/2
ψ arctg
ξr
ξ r ξ p cos ψ
ξ φ ξ p sin ψsin γ
ξ θ ξ p sin ψ cos γ
rw
α arcсos
r

9.

Аппроксимация функции распределения
2
ξ
n1
p
exp
f1
3/2
2πRT1
2 RT1
f
2
ξ
n2
p
exp
3/2
f2
2
RT
2
π
RT
2
2
ξ p (ξ 2r ξ φ2 ξ θ2 )1/2
8
π
если 0<ψ< α
2
π
если
α<ψ<π
2

10.

Уравнение Больцмана для
сферически симметричной задачи
f
f
r
t
r
где
2
2 2 , r , ,
сферической системе координат.
f r f
J,
r r
r
- компоненты вектора скорости в
9a

11.

Интегральное уравнение для сферической геометрии
задачи, полученное из кинетического уравнения Больцмана
9b
1 d 2
r ξ r f dξ
2
r dr
1 2 2
2
f ξ θ ξ φ
ξ φctgθ ξ θξ r
ξ φξ r ξ φξ θctgθ dξ Jdξ
r
ξ r
ξ θ
ξ φ
...dξ ...dξ dξ dξ
r
φ
θ
Весовые функции
1 m
2 mξ r
3
1 2
mξ
2

12.

Результаты интегрирования уравнения
10
Система моментных уравнений
RT1
RT2
n1
n2
0
2π
2π
1d 2
r n1RT1 1 sin 3 n2 RT2 1 sin 3
r dr
n1RT1
n2 RT2
9 1 sin 1 sin 3
4
4
RT1
RT2
r2
2mn1RT1
2mn2 RT2
qr 2
2
2
rw
9 1 sin 1 sin 3
Соотношение для давления пара в пленке
2 P 1 sin α mn1RT1 1 sin α mn2 RT2

13.

Формула для плотности теплового потока
11
2
RTi rw 2 P Ps (Ti ) 1
q 2 Ps (Ti )
1
1
2
2 r 1 1 (rw ri )
2

14.

Сравнение с численным решением
кинетического уравнения Больцмана для тонких пленок
(тестовая задача)
12
При тонких пленках задачу для кинетического уравнения Больцмана можно
считать плоской и одномерной:
f
f
x
J
t
x
При решении уравнения Больцмана граничное условие при
ri фиксировано:
i* 0* 1, Ti* T0* 1.
С учетом этого аналитическая формула для теплового потока приобретает вид:
*
2
P
1
π
1 1
2 1 1 (rw / ri ) 2
2
qw*
В результате решения кинетического уравнения Больцмана получено давление в
пленке
P *и плотность теплового потока на нагревателе q *.

15.

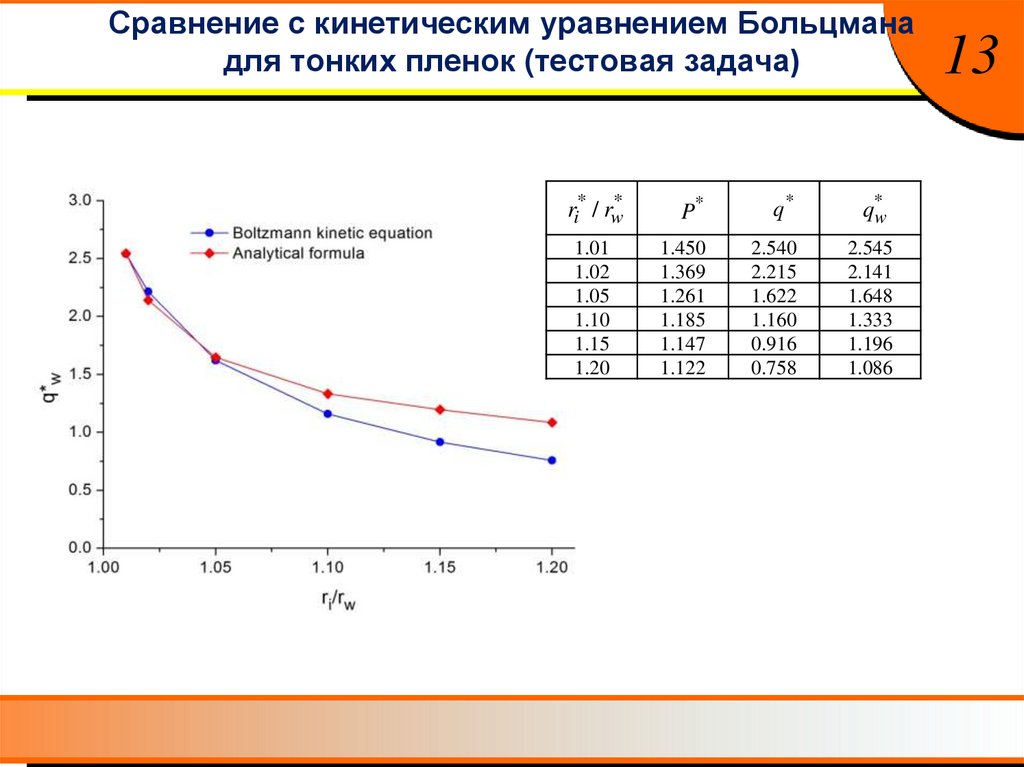
Сравнение с кинетическим уравнением Больцмана
для тонких пленок (тестовая задача)
ri* / rw*
1.01
1.02
1.05
1.10
1.15
1.20
P*
q*
1.450
1.369
1.261
1.185
1.147
1.122
2.540
2.215
1.622
1.160
0.916
0.758
q*w
2.545
2.141
1.648
1.333
1.196
1.086
13

16.

Численное решение уравнения Больцмана
в сферической постановке
Уравнение Больцмана для сферически симметричной задачи имеет вид:
f
f 2 f r f
r
J,
t
r
r r
r
где
2 2 , r , ,
- компоненты вектора скорости в
сферической системе координат.
Однако описывать движение молекул в декартовой системе координат
является более естественным. Перевод компонентов скорости в сферическую
систему
• существенно осложняет вычисление интеграла столкновений;
• требует использования более сложных разностных схем для левой части
уравнения.
14

17.

Численное решение уравнения Больцмана
в сферической постановке
15
Построение конечноразностных схем для сферического уравнения при
сохранении декартовых координат в скоростном пространстве.
Рассмотрим, как частицы, имеющие
ξ( x , y , z ) y
скорость
ξ( x , y , z ) , пронизывают
тонкие сферические слои.
Баланс массы для i-го слоя:
0
z
x
jвход jвыход
ξ
fi fi
Ri2 fi 1 fi Ri2 fi 1 fi ,
2
1
t
Ri3 Ri3
1
2
f - функция распределения, i - номер сферического слоя, Ri , Ri
1
2
внешний и внутренний радиус i -го сферического слоя, соответственно.
где
-

18.

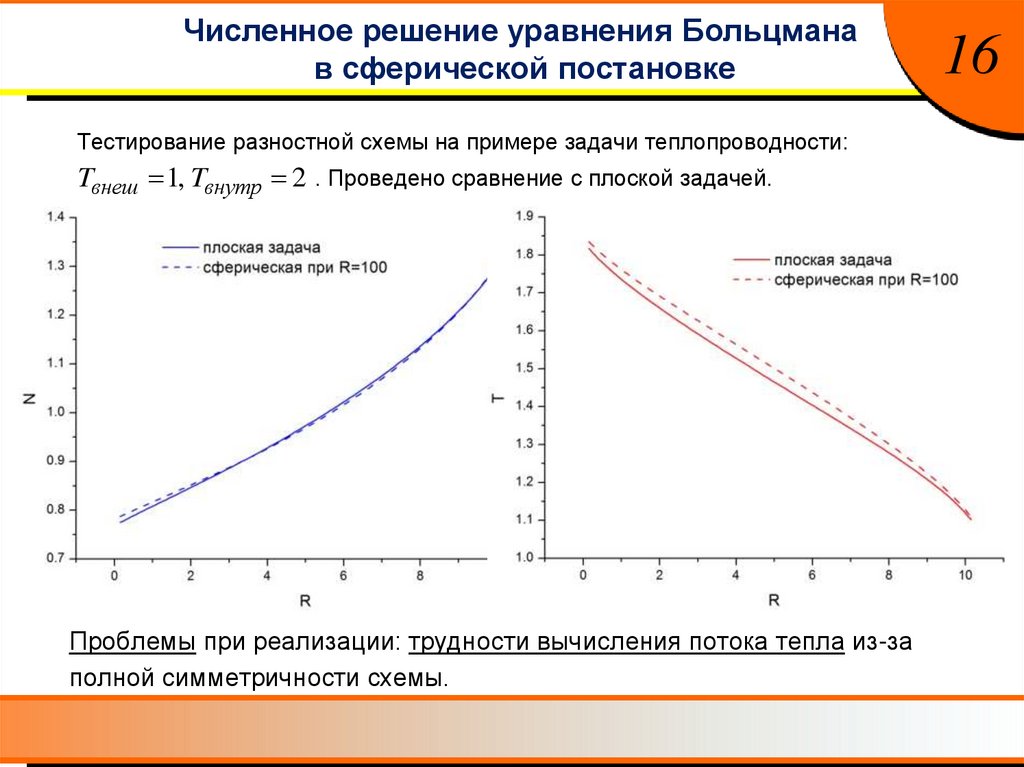
Численное решение уравнения Больцмана
в сферической постановке
Тестирование разностной схемы на примере задачи теплопроводности:
Tвнеш 1, Tвнутр 2 . Проведено сравнение с плоской задачей.
Проблемы при реализации: трудности вычисления потока тепла из-за
полной симметричности схемы.
16

19.

Кипение He-II на сферическом нагревателе
(dw = 4,8 мм, Tb = 1,7 K )
17

20.

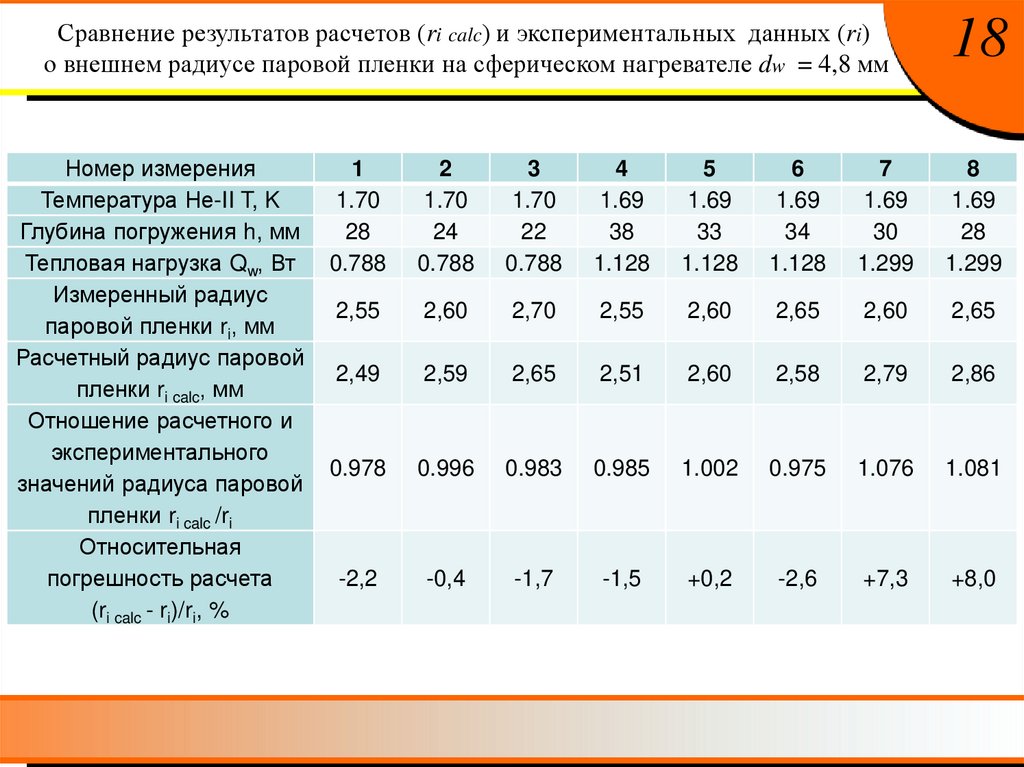
Сравнение результатов расчетов (ri calc) и экспериментальных данных (ri)
о внешнем радиусе паровой пленки на сферическом нагревателе dw = 4,8 мм
Номер измерения
Температура Не-II T, K
Глубина погружения h, мм
Тепловая нагрузка Qw, Вт
Измеренный радиус
паровой пленки ri, мм
Расчетный радиус паровой
пленки ri calc, мм
Отношение расчетного и
экспериментального
значений радиуса паровой
пленки ri calc /ri
Относительная
погрешность расчета
(ri calc - ri)/ri, %
18
1
1.70
28
0.788
2
1.70
24
0.788
3
1.70
22
0.788
4
1.69
38
1.128
5
1.69
33
1.128
6
1.69
34
1.128
7
1.69
30
1.299
8
1.69
28
1.299
2,55
2,60
2,70
2,55
2,60
2,65
2,60
2,65
2,49
2,59
2,65
2,51
2,60
2,58
2,79
2,86
0.978
0.996
0.983
0.985
1.002
0.975
1.076
1.081
-2,2
-0,4
-1,7
-1,5
+0,2
-2,6
+7,3
+8,0

21.

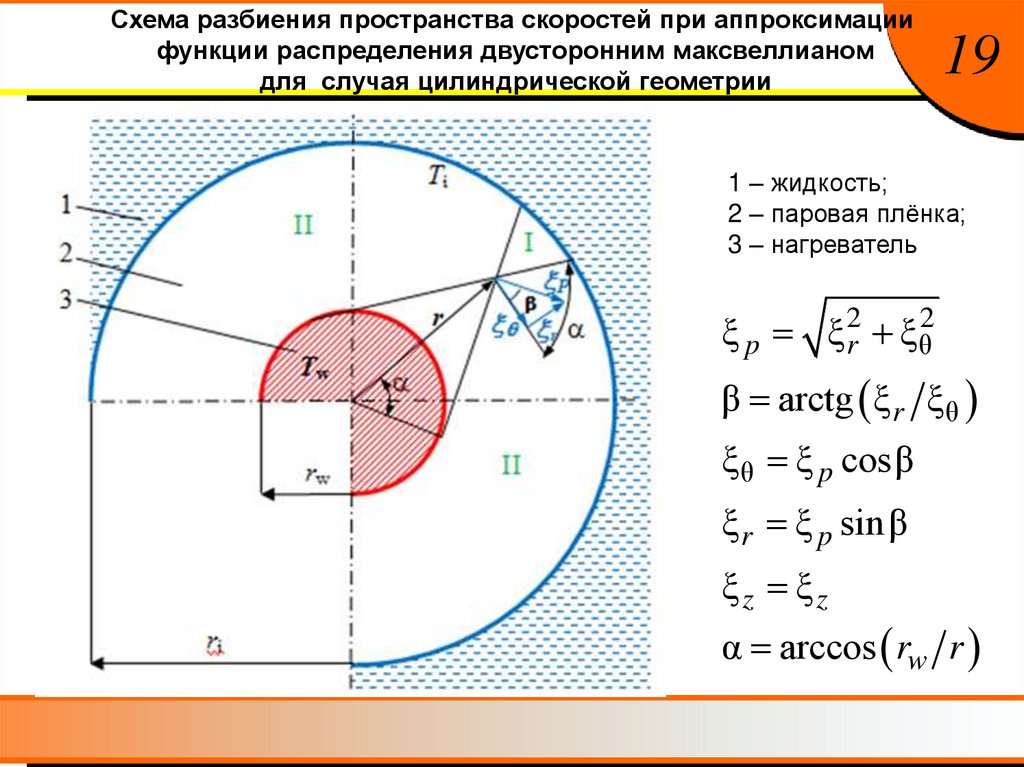
Схема разбиения пространства скоростей при аппроксимации
функции распределения двусторонним максвеллианом
для случая цилиндрической геометрии
19
1 – жидкость;
2 – паровая плёнка;
3 – нагреватель
ξ p ξ r2 ξ θ2
β arctg ξ r ξ θ
ξ θ ξ p cosβ
ξ r ξ p sin β
ξz ξz
α arccos rw r

22.

Интегральное уравнение для цилиндрической
геометрии задачи, полученное из кинетического уравнения
Больцмана
1
1
r ξ r fdξ
r
r r
2
f ξθ
ξ r ξθ
dξ Jdξ,
ξ θ
ξ r
...dξ ...dξ dξ dξ
r
20
θ
z
Весовые функции
1 m
2 mξ r
3
1 2
mξ
2

23.

Аппроксимация функции распределения
21
ξ 2p ξ 2z
n1
exp
если α β π α
f1
3/2
2 RT
2πRT1
1
f
2
2
ξ
ξ
n2
p
z
exp
если π α β 2 π α
3/2
f2
2πRT2
2 RT2
ξ p (ξ 2r ξ θ2 )1/2

24.

Результаты интегрирования уравнения
Система моментных уравнений
RT1
RT2
n1
n2
0
2π
2π
d
d
sin 2 2 n1T1 n2T2 n1T1 n2T2 0
dr
dr
RT1
RT2
r
2mn1RT1
2mn2 RT2
qr
2
2
rw
Соотношение для давления пара в пленке
2 P mn1RT1 2 mn2 RT2 2
22

25.

Формула для плотности теплового потока
23
2
2
P
P
(
T
)
1
RTi rw
s i
q 2 Ps (Ti )
1 1
2 r 1 (2/π) arccos rw /ri

26.

Пленочное кипение Не-II на цилиндре
24

27.

Примеры пленочного кипения на цилиндре
25

28.

ВСЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЕ ФОРМУЛЫ ДЛЯ ТЕПЛОПЕРЕНОСА ПРИ ПЛЕНОЧНОМ КИПЕНИИ
И ПОСТОЯННОЙ ТОЛЩИНЕ ПАРОВОЙ ПЛЕНКИ, Т.Е. НУЛЕВОМ ПОТОКЕ МАССЫ
Греющая
поверхность
Плоскость
Вид формулы
Линейная
4
qi
P Ps (Ti ) 2RTi
π
RTi P
8 Ps (Ti )
1
2π Ps (Ti )
Нелинейная
qi 8 P
RTi P
1
2 Ps (Ti )
Формула А.П. Крюкова.
Формула Лабунцова–Муратовой. Публикация в 1969 г.
Цилиндр
26
Публикация в 2000 г.
2
r
π
RTi w
π
r π 2arccos(rw ri )
q 4( P Ps (Ti ))
Вывод в 2014 г., публикация в 2016 г.
Общая формула через разность температур
2
d
Tw Ti 1
q Ps (Ti ) RTi w
π
2r 1 2 d w ln 2ri
15 lб
dw
2
RTi rw 2 P Ps (Ti ) 1
q 2 Ps (Ti )
1 1
2 r 1 (2/π) arccos rw /ri
Вывод в 2014 г., публикация в 2016 г.
Вывод в 1998 г., публикация в 2014 г.
Труды Шестой Российской национальной конференции по
теплообмену. 27–31 октября 2014 г. Москва. НИУ «МЭИ».
Издательский дом МЭИ. CD-ROM публикация. Секция 4.
при Kn
q 2 Ps (Ti )
rw
RTi Tw
1
2π Ti
r
П.В. Королев, А.П. Крюков. Описание теплопереноса через
цилиндрическую межфазную поверхность жидкость–пар //
Теплофизика высоких температур.– 2016.– Т. 54. – №1.– С. 73–80.
при Kn 0
q
Сфера
15 Ps (Ti )
lб
2 Ti
RTi
Tw Ti
2π r ln 2ri d w
2
rw
4
r
q
( P Ps (Ti )) 2 RTi
π
1 1 (rw ri )2
Вывод в 2020 г.
2
2
RTi rw
2 P Ps (Ti ) 1
q 2 Ps (Ti )
1 1
2 r 1 1 (rw ri )2
Вывод в 2015 г., публикация в 2020 г.