Похожие презентации:
Физика конденсированного состояния
1.
Физика конденсированногосостояния
Литература
Основная
1. Крюков А.П. Элементы физической кинетики: учебное пособие. М.:
МЭИ, 1995.
2. Крюков А.П. Элементы гидродинамики и теплопереноса в гелии II:
учебное пособие. М.: МЭИ, 2004.
3. Дмитриев А.С. Основы криофизики конденсированных систем: учебное
пособие. М.: МЭИ, 2006.
2.
Физика конденсированногосостояния
Литература
Дополнительная
1. Коган М.Н. Динамика разреженного газа. М.: Наука, 1967.
2. Лифшиц Е.М., Питаевский Л.П. Физическая кинетика. Сер. Теоретическая физика. Т.10. М.:
Наука, 1979
3. Аристов В. В. , Черемисин Ф.Г. Прямое численное решение кинетического уравнения
Больцмана. М.: ВЦ РАН, 1992.
4. Крюков А.П., Левашов В.Ю., Шишкова И.Н., Ястребов А.К. Численное решение
кинетического уравнения Больцмана в инженерной практике: учебное пособие. М.: МЭИ, 2005.
5. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. Сер. Теоретическая физика. Т.6. М.: Наука, 1988
(глава XVI, стр.706-730).
6.
Халатников И.М. Теория сверхтекучести. М.: Наука, 1971.
7.
Паттерман С. Гидродинамика сверхтекучей жидкости. М.: Мир, 1978.
8.
Киттель Ч. Введение в физику твердого тела. М.: Наука, 1978.
9.
Займан Дж. Принципы теории твердого тела. М.: Мир, 1974.
3.
Физика конденсированногосостояния
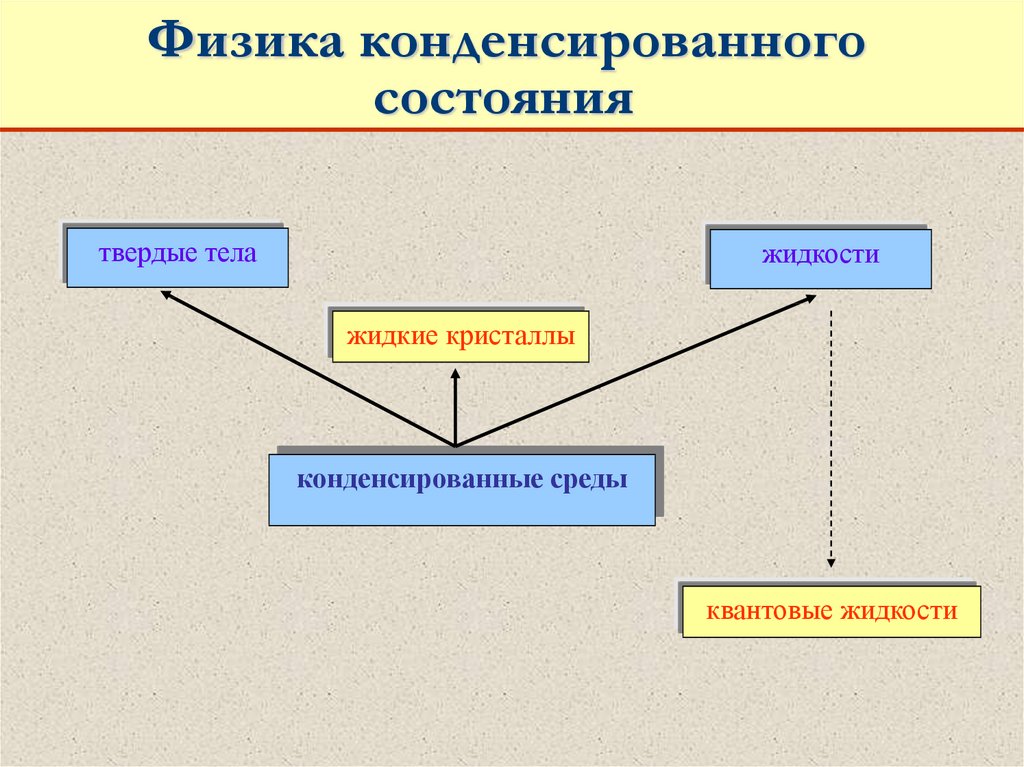
твердые тела
жидкости
жидкие кристаллы
конденсированные среды
квантовые жидкости
4.
Физика конденсированногосостояния (ФКС)
Занимается фундаментальным изучением
различных конденсатов.
Предмет ФКС – свойства конденсированных
сред и процессы в них.
5.
Лауреаты Нобелевской премиив области физики низких температур
Имя
Год
открытия
Год награждения
Ландау Л.Д.
1941
1962
Капица П.Л.
1938 (39)
1978
Ли Д., Ошерофф Д.,
Ричардсон Р.
1972
1996
Беднорц Г., Мюллер А.
1986
1987
Корнелл Э., Вайман К.,
Кеттерли В.
1995
2001
Абрикосов А.А.,
Гинзбург В.Л., Леггетт
А.Дж.
1957
2003
6.
Физика конденсированногосостояния
Конденсированная среда – система частиц,
сильно взаимодействующих друг с другом.
7.
Физика конденсированногосостояния
Состояния вещества
Газ
Жидкость
Твердое
тело
Порядок
Хаос
Ближний
Ближний и
дальний
Время
ст~ 10-13с
мс~ 10-9с
10-8с
10-13с
Энергия
Uср<<Eср
Uср ~ Eср
Uср > Eср
8.
Физика конденсированногосостояния
Часть 1
9.
12
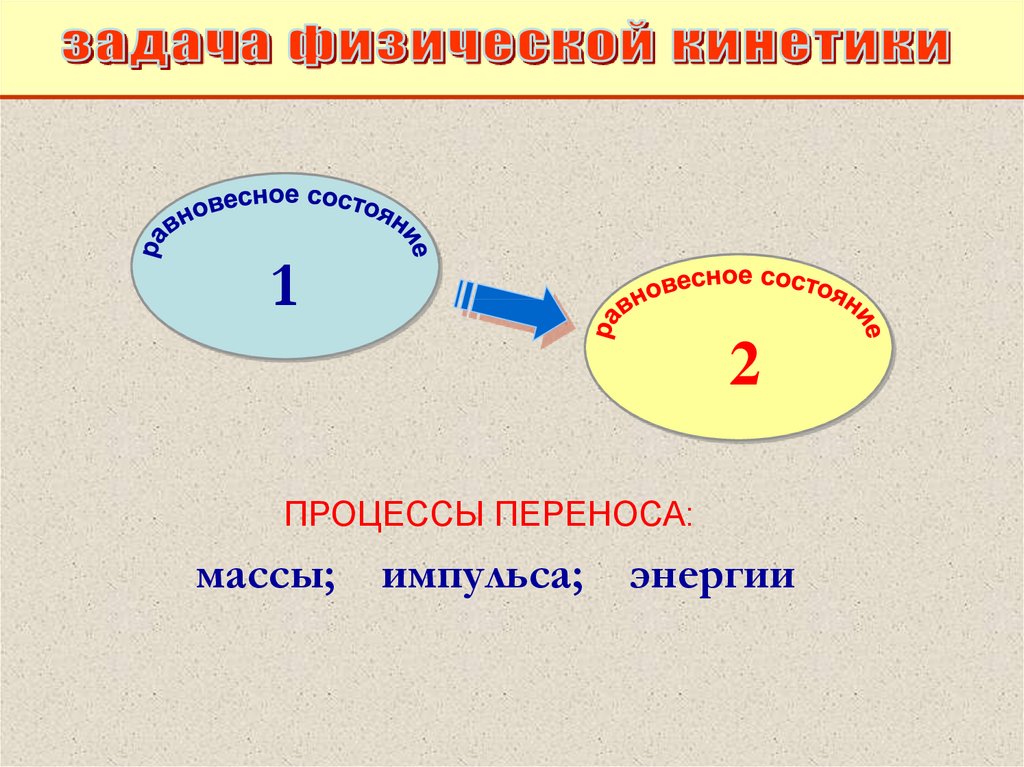
ПРОЦЕССЫ ПЕРЕНОСА:
массы; импульса; энергии
10.
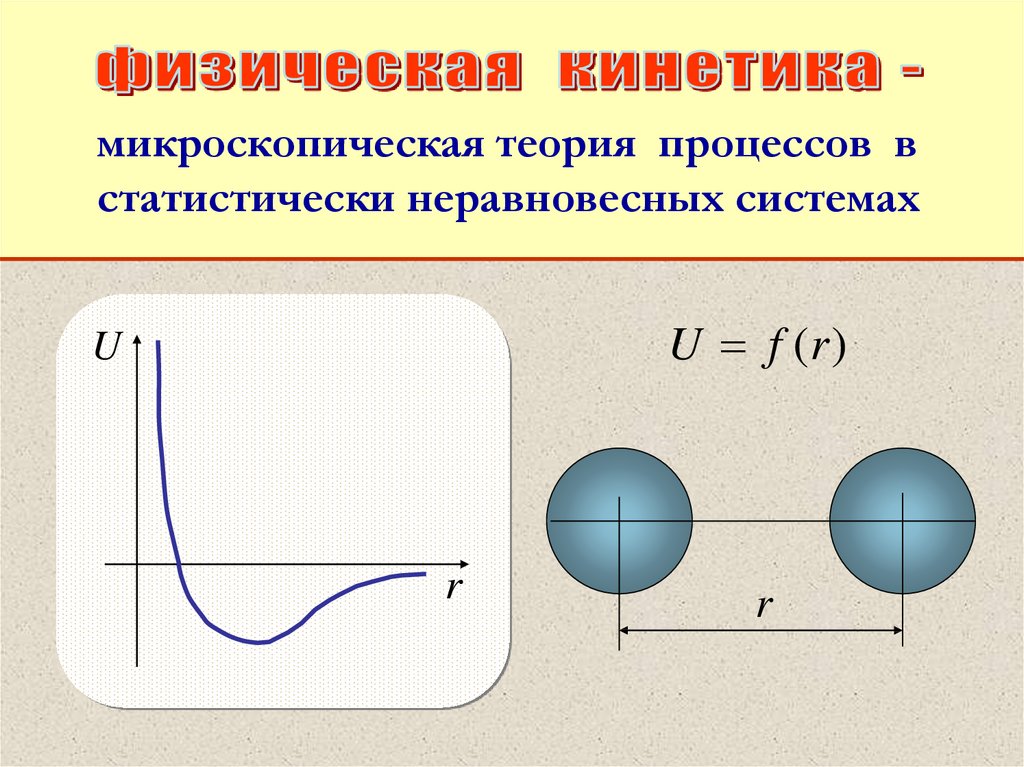
микроскопическая теория процессов встатистически неравновесных системах
U f (r )
U
r
r
11.
12.
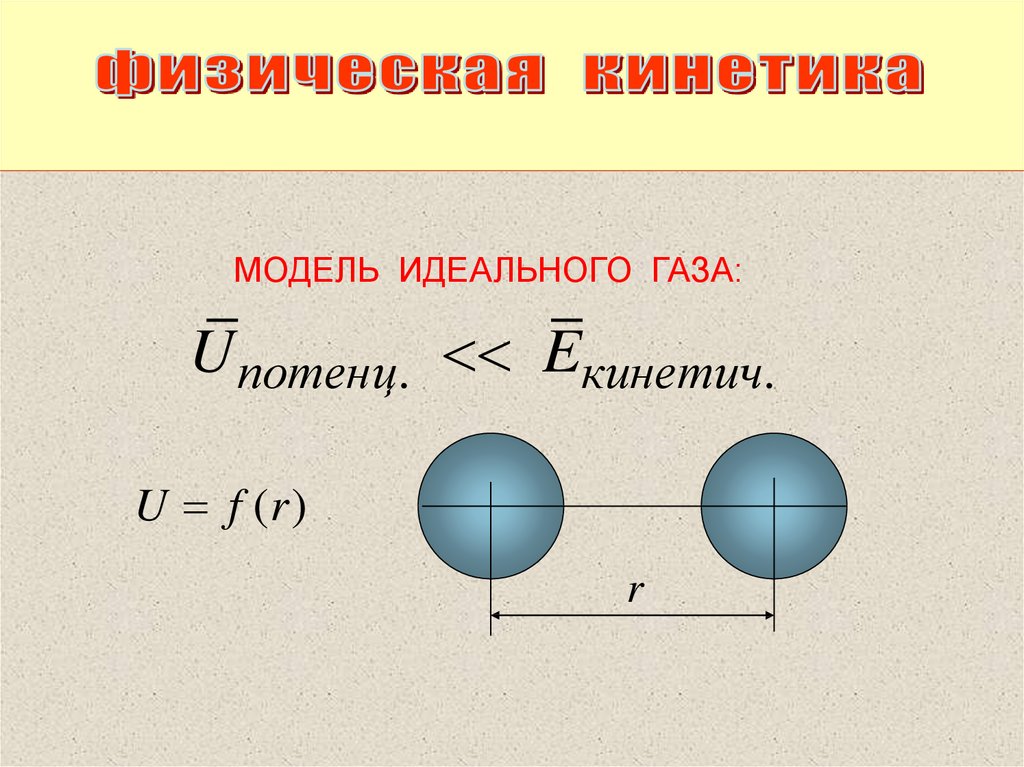
МОДЕЛЬ ИДЕАЛЬНОГО ГАЗА:U потенц. Eкинетич.
U f (r)
r
13.
ТВЕРДЫЕ УПРУГИЕ ШАРЫU f (r)
U
d
r
U при r d
U 0 при r d
(1)
14.
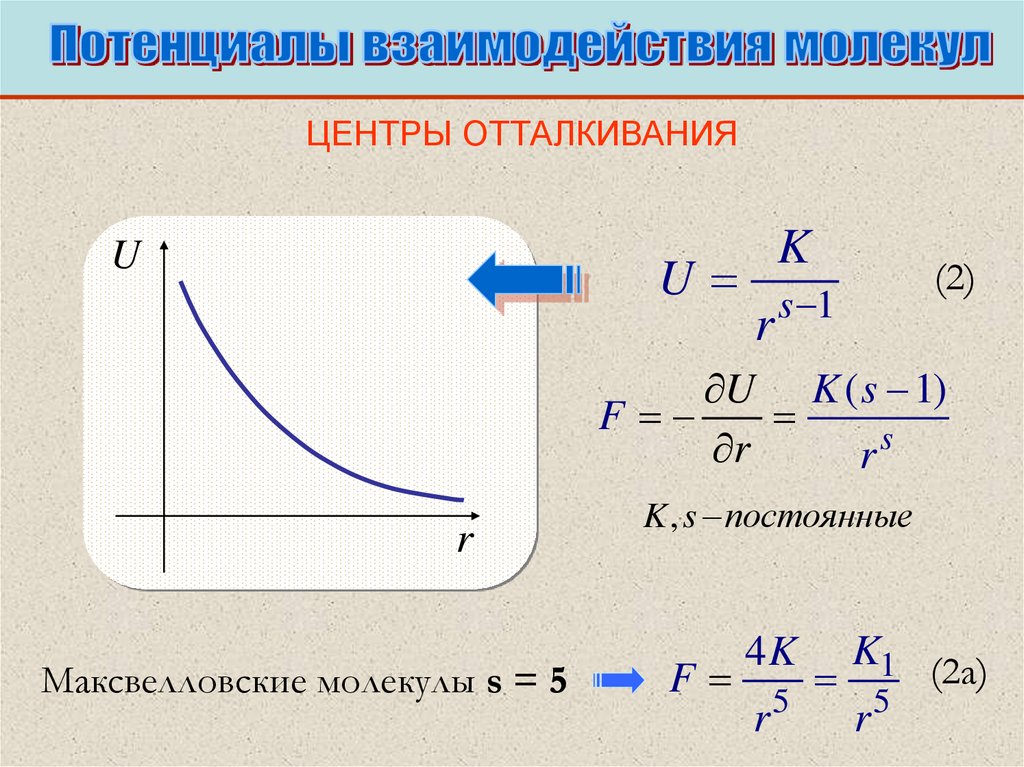
ЦЕНТРЫ ОТТАЛКИВАНИЯU
K
U
r
s 1
(2)
U K ( s 1)
F
s
r
r
r
Максвелловские молекулы s = 5
K , s постоянные
K1 (2a)
F 5 5
r
r
4K
15.
ЛЕННАРД-ДЖОНСА(3) U 4
U
d / r
12
d / r
6
d / r
притяжение
12
отталкивание
d / r
F
6 2d
6
6
26
d
7
2.4
r
d
r
16.
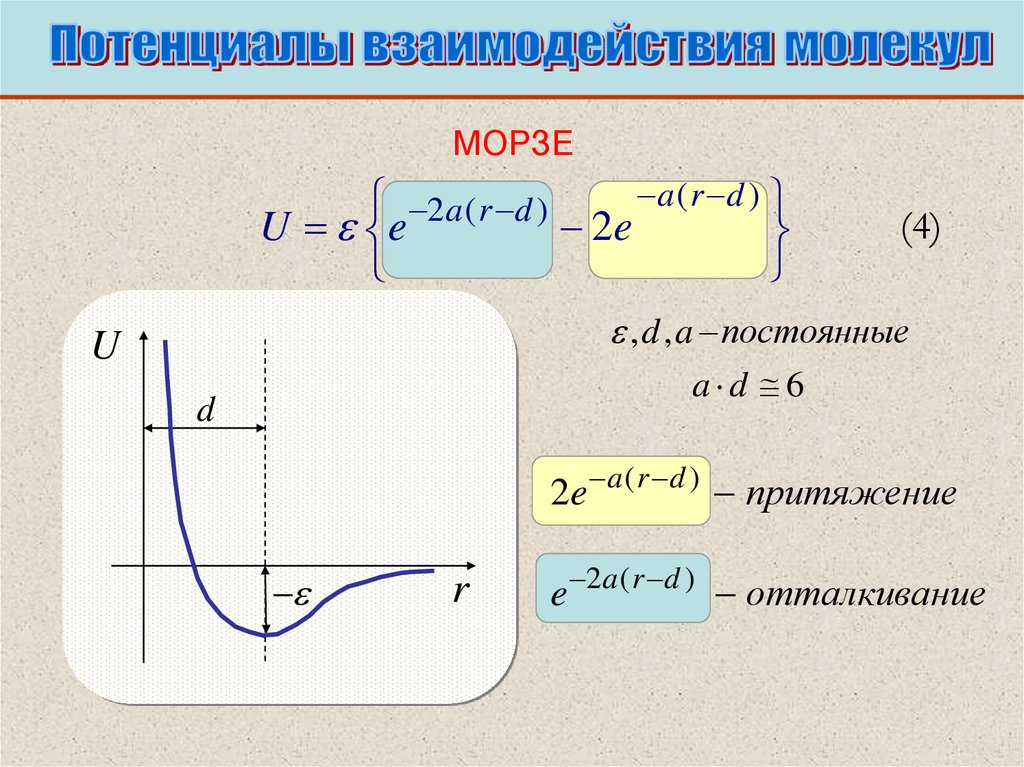
МОРЗЕa ( r d )
2a ( r d )
U e
2e
(4)
, d , a постоянные
U
a d 6
d
2e a ( r d ) притяжение
r
e 2a ( r d ) отталкивание
17.
U f (r)СЕЗЕРЛЕНДА
U
d
U при r d
r
U d / r m
при r d
, d , m постоянные
(5)
18.
6f x , , t dxd есть ожидаемое число молекул в
объеме dxd , координаты
которых находятся в интервале
от x до x dx , а скорости
в интервале от до d .
f x , , t функция семи переменных:
x , y , z , x , y , z , t.
19.
РАВНОВЕСНОЕ МАКСВЕЛЛОВСКОЕ РАСПРЕДЕЛЕНИЕ1
f n
2
RT
3/ 2
2 2 2
x
y
z
exp
2 RT
n числовая плотность;
T температура;
R индивидуальная газоваяпостоянная.
,(7)
20.
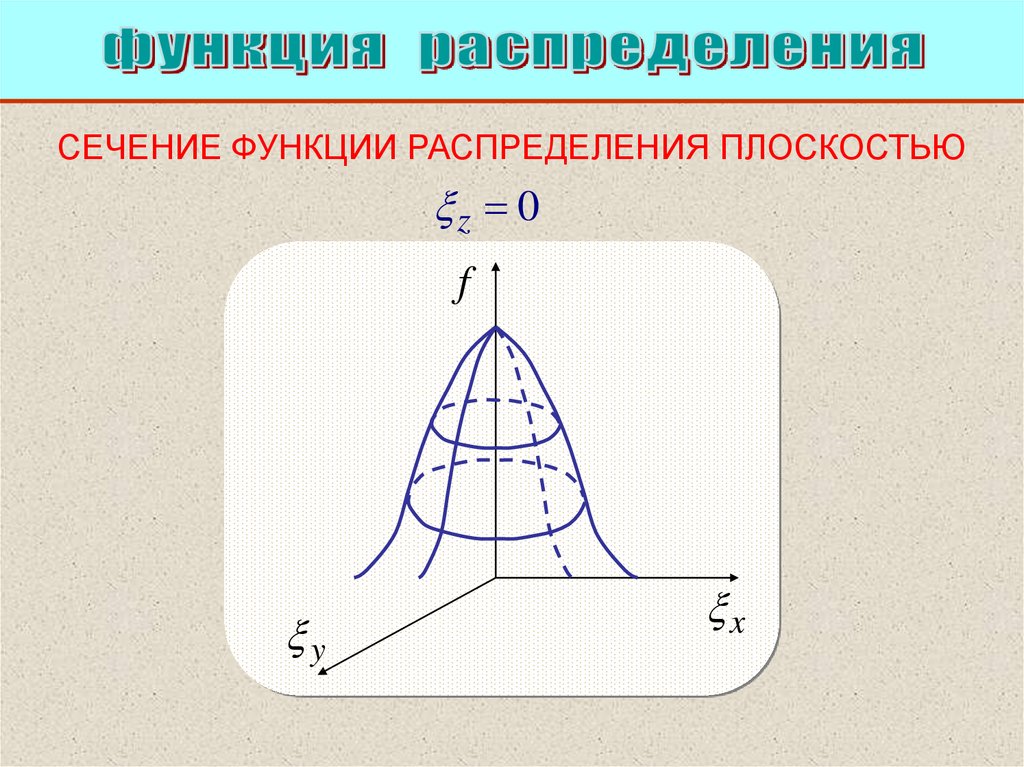
СЕЧЕНИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ПЛОСКОСТЬЮz 0
f
y
x
21.
СЕЧЕНИЯ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ПЛОСКОСТЯМИz 0, y1 const, y 2 const : z 0, f1 const , f 2 const :
f
y
y1
f1
f2
y2
x
y 2 y1
x
f 2 f1
22.
Момент функции распределения –это интеграл по пространству скоростей
от этой функции, взятый с определенным весом.
M ( f )
f d
некоторая функция
(8)
23.
ПРИМЕРЫ МОМЕНТОВ ФУНКЦИИ РАСПРЕДЕЛЕНИЯm
f d ;
(9)
плотность газа; m масса молекулы
jx u x m
f x d
(10)
jx x ая проекция плотности потока массы;
u x x ая проекция скорости потока газа;
24.
Моменты функции распределенияf t , x, dxd
ожидаемое число молекул в элементе объема
физического пространства dx около точки x ,
обладающих скоростями в элементе пространства
скоростей d около точки
f t , x, d dx – для единичного объема
f
m
fd
x
0
m f t, x,
d x d y d z
Другие моменты
ux m
m
f x d ; T
u
3R
2
fd
25.
ПРИМЕРЫ МОМЕНТОВ ФУНКЦИИ РАСПРЕДЕЛЕНИЯkl m
k l f d ;
(11)
m
Ex
2
f 2 x d
(12)
2 x2 y2 z 2
26.
Pxy mcx c y f d ;
(13)
cx x u x ,
cy y u y
u x x ая проекция скорости потока газа;
u y y ая проекция скорости потока газа;
1
qx m
2
c 2c x f d
(14)
3
1
kTn m
2
2
c 2 f d
c 2 cx 2
(15)
c y 2 cz 2
27.
28.
X 0 ff
f
J ,(16)
t
x
m
X0
f
f
f
f
f
f
f
a
x
y
z
J
,(16
)
t
x
y
z
m
x y z
ИНТЕГРАЛ СТОЛКНОВЕНИЙ:
(17) J
2
0 0
f f 1 ff1 g bdbd d 1
f f t , x , ; f1 f t , x , 1 ; f f t , x , ; f1 f t , x , 1
29.
11
30.
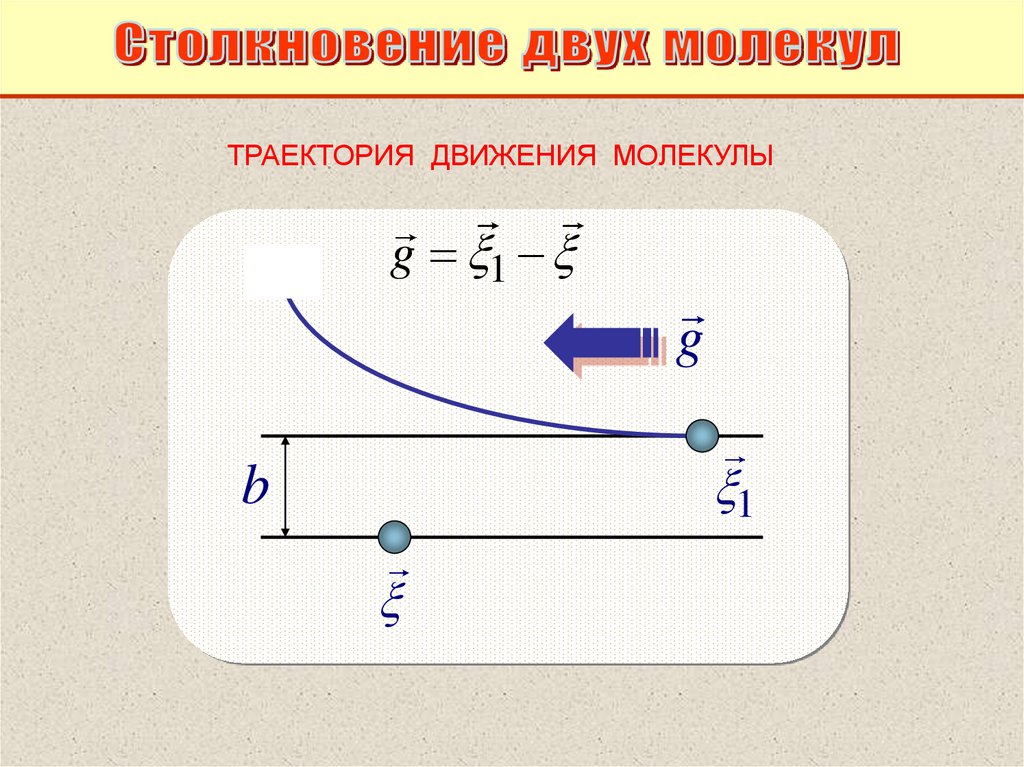
ТРАЕКТОРИЯ ДВИЖЕНИЯ МОЛЕКУЛЫg 1
g
1
b
31.
РАССМОТРЕНИЕ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ ВЦИЛИНДРИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ
g
1
db
d
b
32.
(18) IJd x d y d z
1
a
(19 ) I
4
1 1 f f 1 ff1 g bdbd d 1d
1
(19 ) I
2
б
1 1 ff1 g bdbd d 1d
33.
Для сумматорных инвариантов:1 1 0
Инварианты столкновений: 0 m
1 m x
2 m y
3 m z
1
4 m 2
2
Если - сумматорный инвариант, то
2
Am Bm C
34.
Hf ln f d x d y d z (20)
Hx
1
I ln f
4
x f ln f d
(21)
ln f ln f1 ln f ln f1 f f 1 ff1 g bdbd d 1d
H H x
I 1 ln f
t
x
H
0 (22a )
t
H H x
0 (22)
t
x
H x
0 (22б )
x
35.
H H x0
t
x
I 1 ln f 0
1 ln f Am 2 Bm C
n
f d ; nu x
m
T
3kn
f x d
nu y
f y d
nu z
f z d
[( x u x ) 2 ( y u y ) 2 ( z u z ) 2 ] f d
3
2
m
m
2
2
2
f n
exp
(
u
)
(
u
)
(
u
)
x
x
y
y
z
z
2
kT
2
kT
36.
МОДЕЛЬНЫЕ УРАВНЕНИЯУравнение Бхатнагара, Гросса, Крука
f
f
f0 f (23)
t
x
— постоянный множитель, частота столкновений;
f0 – равновесная максвелловская функция распределения,
c параметрами n0, ux0, uy0, uz0, T0, которые определяются из:
f0 d f d ;
f 0 u
2
f0 i d f i d
d f u
2
d , где
(i x, y , z );
f 0 i d
ui
f0 d
37.
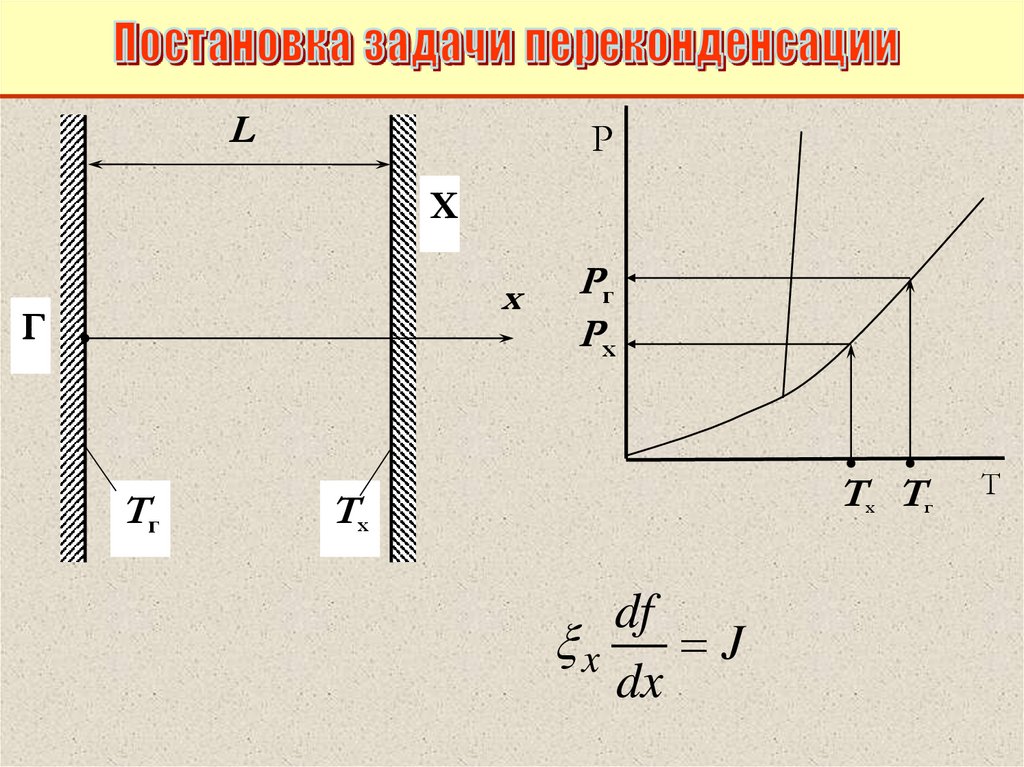
LP
Х
х
Г
Tг
Рг
Рх
Tх Tг
Tx
df
x
J
dx
Т
38.
Принятие аппроксимации функции распределенияn1 x
2
exp
f1
x 0
32
2 RT1 x
2
RT
x
1
(24)
n2 x
2
exp
x 0
f2
32
2 RT2 x
2
RT
x
2
Cила взаимодействия молекул
F K1 r 5
Четырехмоментная аппроксимация
1
1 m; 2 m x ; 3 m 2 ; 4 m x 2
2
df
m x
mJ ,
Умножение
dx
39.
Интегрированиеdf
m x d
dx
d
m
x f d
dx
mJd ,
d x
m
dx
1
x2
и т.п.
f d
x2 f d
40.
d x0
m
dx
d
m
m
m
2
x
0
dx
d x
2
dx
d x2 2
dx
2
0
m I x
2
41.
jxx
m
П xх
2
x
m
x
d
m
2
а
(25 )
(25б )
Ех
2
m
2 2
x
dx
в
(25 )
m I x
2
г
(25 )
42.
x xx
Интеграл Пуассона
e
0
2
x
1
dx
2
43.
jxRT1
RT2
n1
n2
2
2
m
П xх
1
1
n1RT1 n2 RT2
2
2
m
(26а )
б
(26 )
RT1
RT2 Е х
2n1RT1
2n2 RT2
(26в )
2
2
m
d 5
2 5
2
2
n
RT
n
RT
I
(*)
2
2
x
1 1
dx 2
2
44.
I x2
1
2
x 1 1 2 x 2 x1 12 x
1
2 K1 s 1
b
m
g
g bdb
m
При s=5
g
ff1 g bdbd d 1d
1
2 K1 s 1
2
s 1
2
2 K1 s 1
2
db
m
1
4
s 1 d
1
2 K1 2
g bdb
d
m
g
2
s 1 d
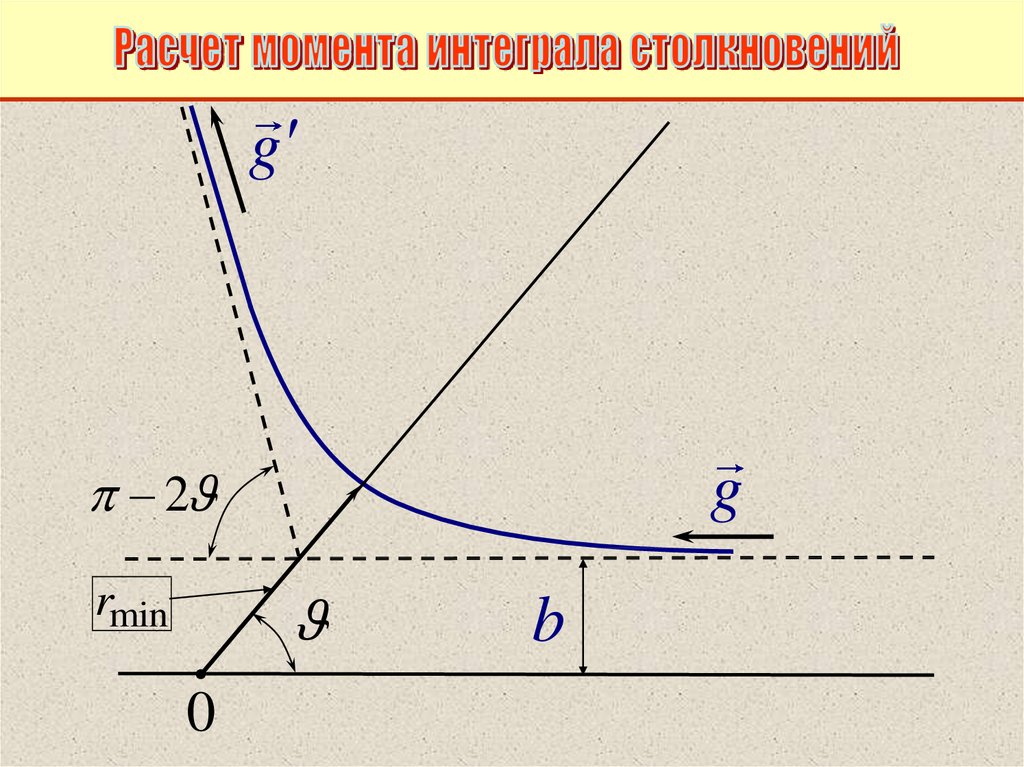
45.
g2
g
rmin
0
b
46.
2g b sin
2
cos dbd A2
2
0 0
I x 2 2 A2
I x
2
A
4 2
m
K1
, где A2 =1,3682
2m
K1
1 x 2 2 x 2 x x2
2m
n1 x +n 2 x
K1
5 xx
Ex jx
, где ρ=m
2m m 2
m
2
d 5
4 A2
2 5
2
n1 RT1 n2 RT2
dx 2
2
m
K1
5 xx
г
E
j
,
(26
)
x
x
2m m 2
m
47.
n1T11 2 n2T21 2 j x(27 а )
n1T1 n2T2 П xх
(27б )
n1T13 2 n2T23 2 Е х
(27в )
d
16
K1
2
2
n1T1 n2T2
A2
dx
2m
5 2
lб
nб
RTб
RTб
2 2 nб A2 K1 2m
5
E x n j x xx (**)
8
48.
d4 1
5
2
2
n1T1 n2T2
Ex n jx xx
dx
8
5 lб
d n1T12 n2T22
0,45
5
г
E
n
j
,
(27
)
x
x xx
dx
Knб
8
где x x / L, Knб lб / L, 0,45 4 (5 )
49.
n1 1 N1 n2 1 N2 T1 1 t1 T2 1 t2N1 t1 2 N 2 t2 2 j x
(28а )
2 N1 t1 N 2 t2 П xх
(28б )
3
3
N1 t1 N 2 t2 Е х
2
2
(28в )
d N1 2t1 N 2 2t2
0,45
5
E
jx
x
dx
Knб
4
(28г )
t2 t1 Ex jx (29)
N2
xx
N1
N 2 N1 3 jx
2
t1 5 jx 3 Ex 1 (30a )
2
4
4
xx
2
t1
Ex
4
jx
4
1 (31)
Ex
2
(30)
50.
51.
Соотношение неопределенностей Гейзенберга:p x
(1)
Неопределенность (флуктуации) энергии атома:
p
E
2m
2
2
2m x
(2)
2
52.
40Твердый He
Верхняя -точка
(T=1,76K; 29,8атм)
P, атм
30
Жидкий He I
Кривая -перехода
20
10
Жидкий He II
Критическая точка
(T=5,20K; 2,264атм)
-точка
(T=2,177K; 0,0497атм)
0
0.0
Газообразный He
1.0
2.0
3.0
T, K
4.0
5.0
6.0
P
Т
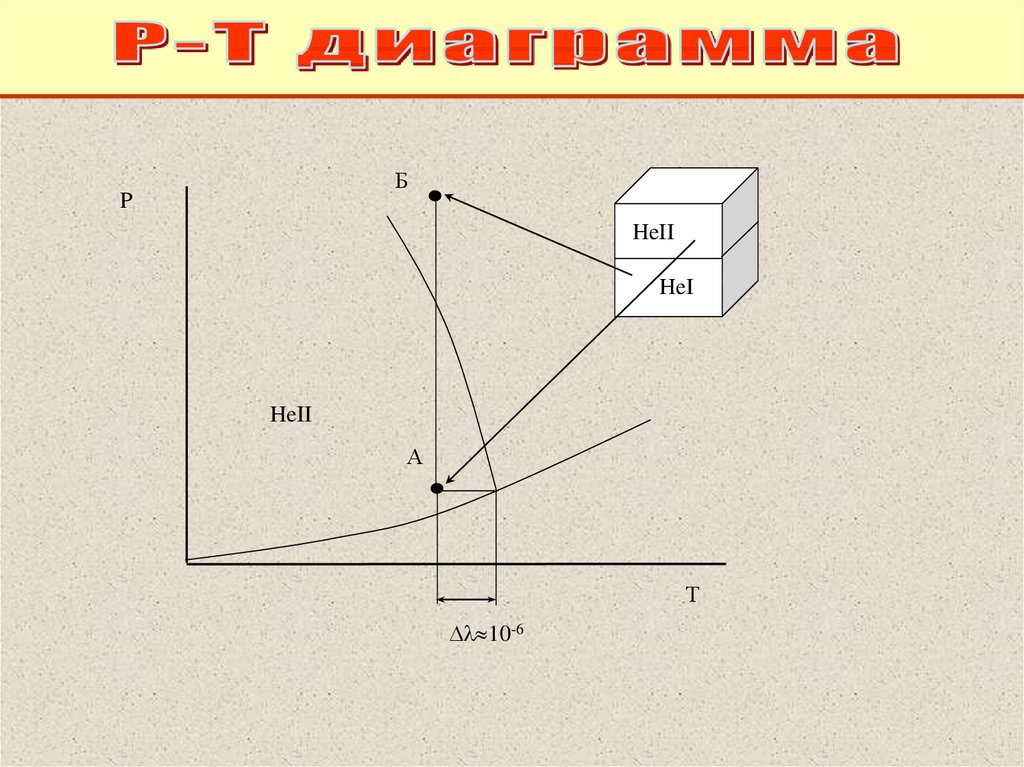
53.
БP
HeII
HeI
HeII
А
Т
10-6
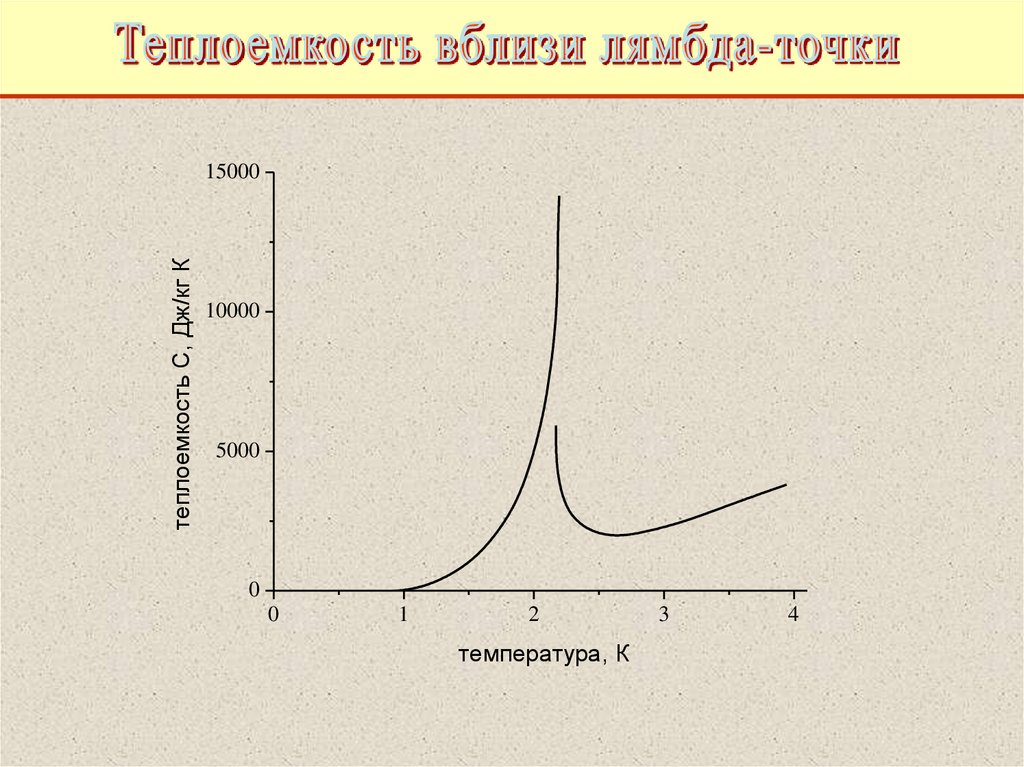
54.
теплоемкость C, Дж/кг К15000
10000
5000
0
0
1
2
температура, К
3
4
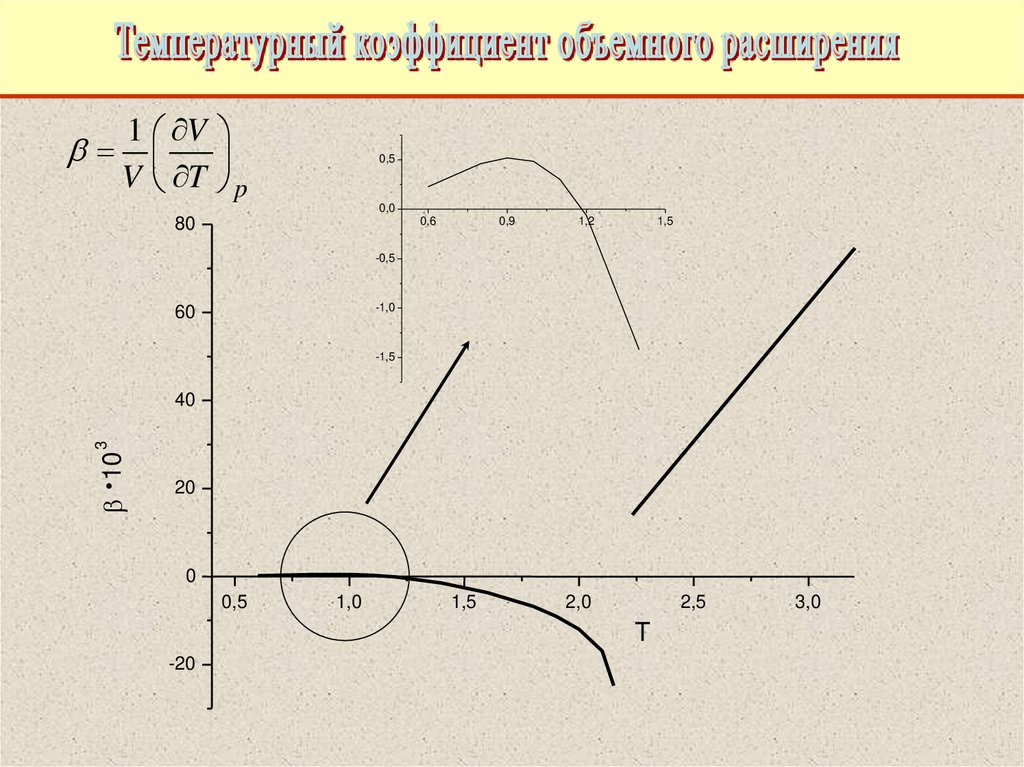
55.
1 Vb
V T p
0,5
0,0
80
0,6
0,9
1,2
1,5
-0,5
-1,0
60
-1,5
b 10
3
40
20
0
0,5
1,0
1,5
2,0
2,5
T
-20
3,0
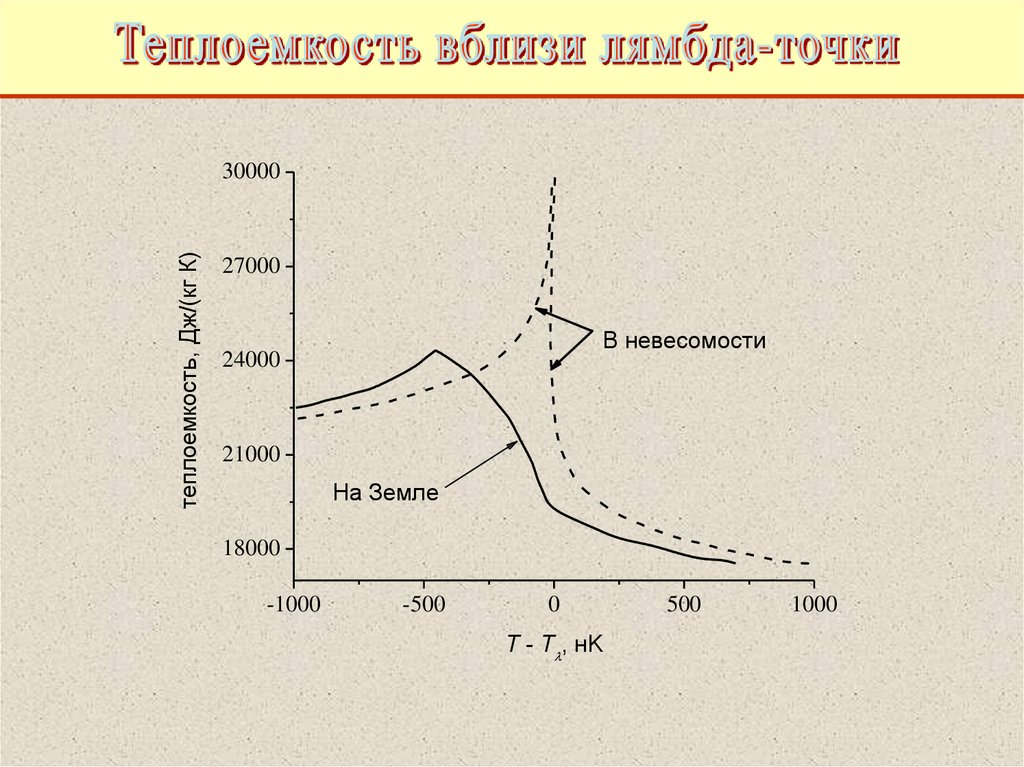
56.
теплоемкость, Дж/(кг К)30000
27000
В невесомости
24000
21000
На Земле
18000
-1000
-500
0
T - T , нK
500
1000
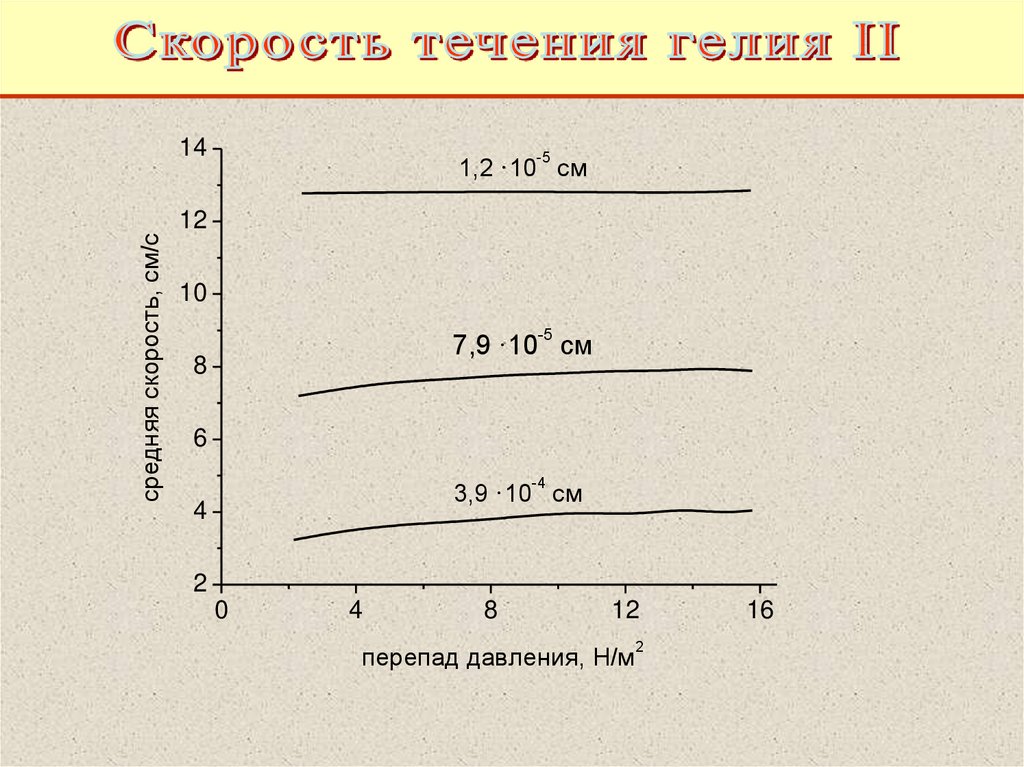
57.
средняя скорость, см/с14
-5
1,2·10 см
12
10
-5
7,9·10 см
8
6
-4
3,9·10 см
4
2
0
4
8
12
перепад давления, H/м
2
16
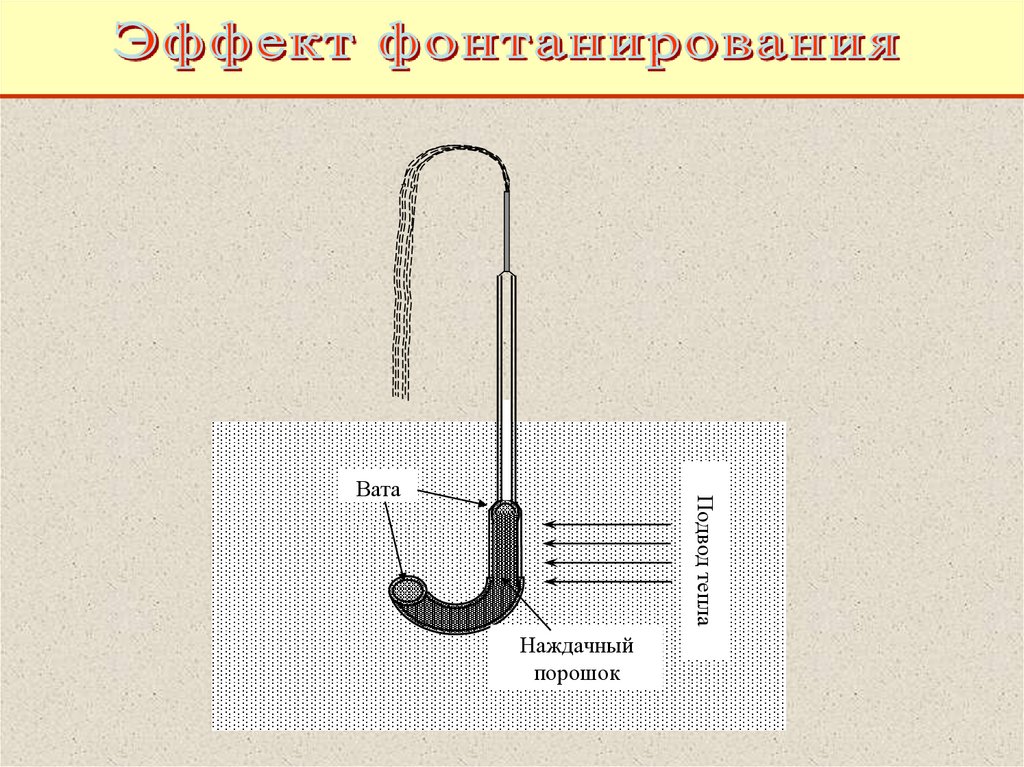
58.
Подвод теплаВата
Наждачный
порошок
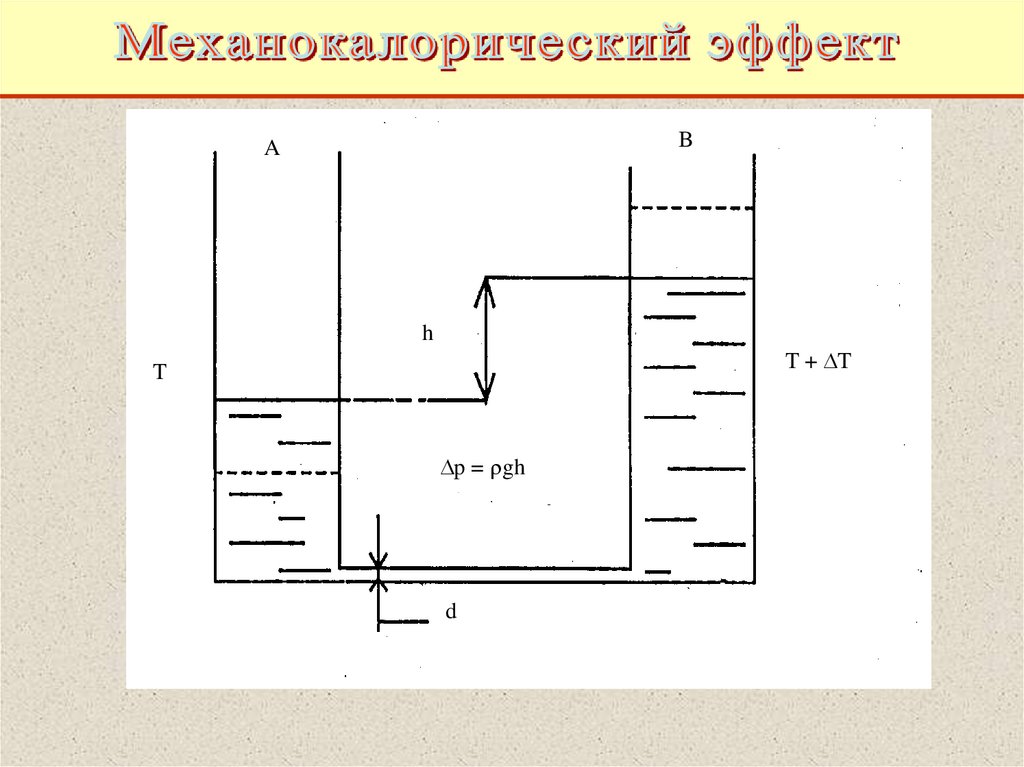
59.
BA
h
T + T
T
p = gh
d
60.
pd = 10-7 –10-6м
T + T
T
TA
H
B
A
TB
S
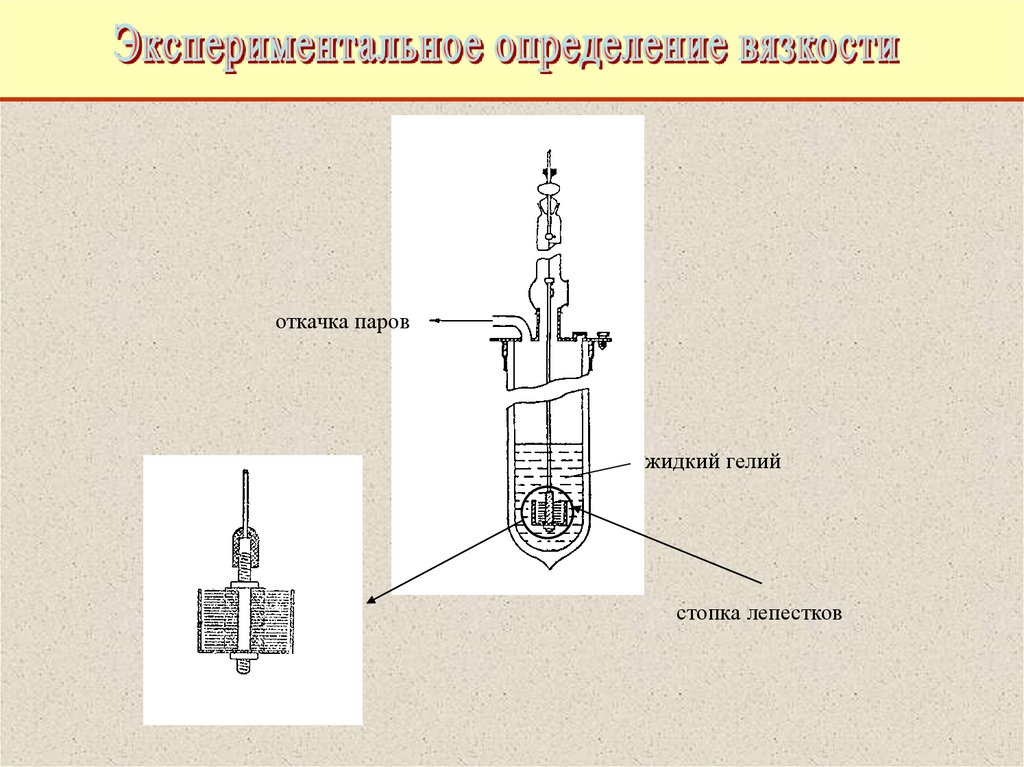
61.
откачка паровжидкий гелий
стопка лепестков
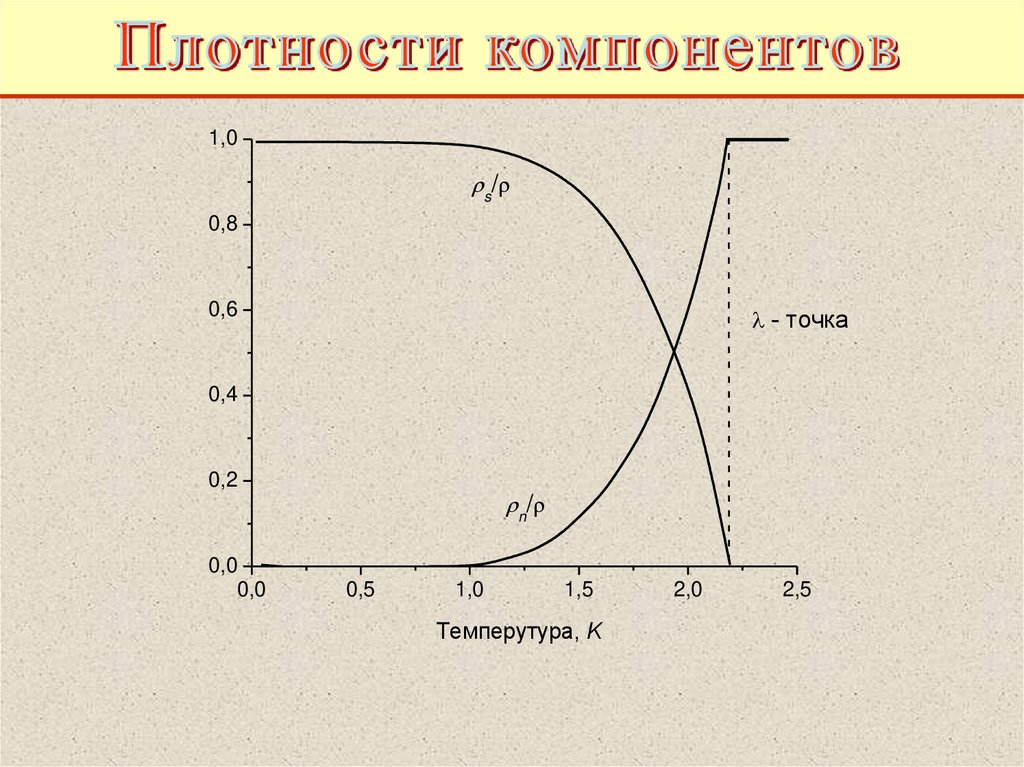
62.
1,0s /
0,8
0,6
- точка
0,4
0,2
0,0
0,0
n /
0,5
1,0
1,5
Темперутура, K
2,0
2,5
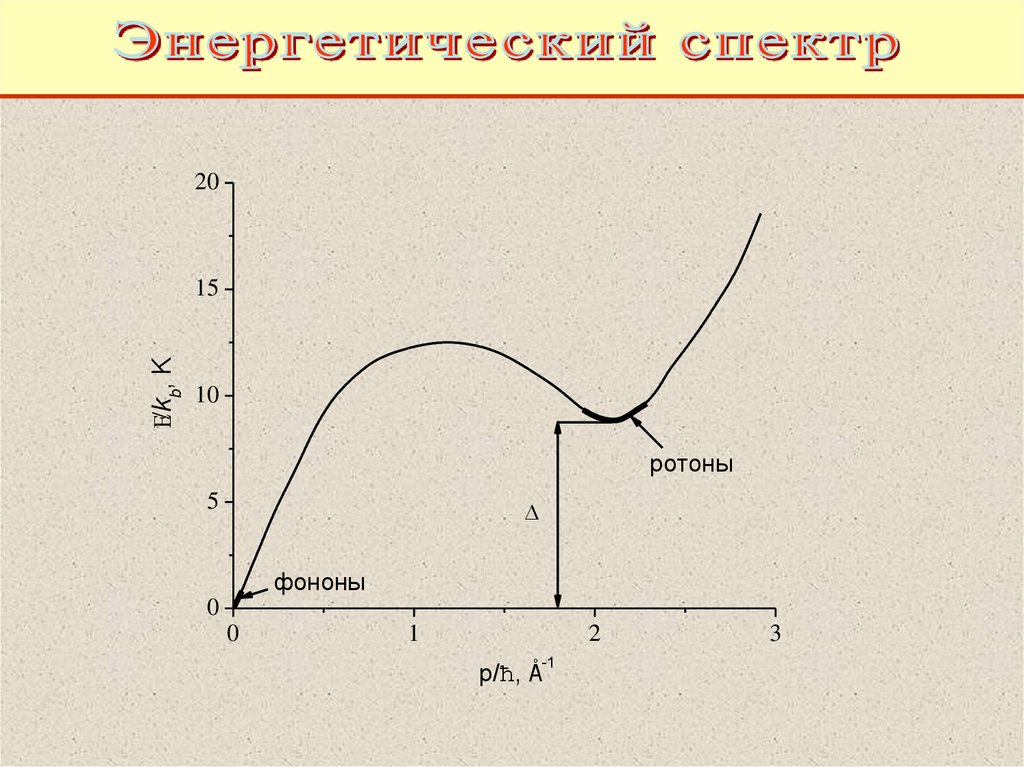
63.
20/kb, K
15
10
ротоны
5
фононы
0
0
1
2
p/ћ, Å
-1
3
64.
n sdiv j 0 (3)
t
Vs
Vs2
grad
0 (5)
t
2
ji ik
0 (4)
t xk
S
div F 0 (6)
t
e*
div E 0 (7)
t
Требуется найти j, ik , , E,F
65.
В покоящейся системе координат j V; (8)в движущейся системе координат j0 V Vs . (9)
j j0 Vs
2
V Vs
V
Vs2
Vs
e* e e
e*0 Vs V
VVs
2
2
2
2
Vs 2
Vs 2
e*0 Vs V Vs
e*0 j0Vs
(10)
2
2
2
d e*0 d Td S Vn Vs dj0 (11)
66.
j0 n Vn Vs (12)j nVn sVs (13)
ik ik p nVniVnk sVsiVsk (14)
(15)
F = SVn (16)
q =T F
q = STVn (17)
67.
q 0x
Vny
He II
0
y 0
0
y 0
Vnx y 0 0
y
q 0
Vsy
Vny
Vsy
y 0
y 0
qy
ST
n q y
s ST
68.
j0 (18)
t x
j p
0 (19)
t x
S
Vn
S
0 (20)
t
x
Vs
0 (21)
t
x
Дифференцируя (18) по t и (19) по x,
2
2 j
2 j
2 p
получаем 2
и
2
t
t x
x t
x
2 2 p
2 (22)
2
t
x
69.
Из (20) SS
V
S n 0 (23)
t
t
x
Из (18) и (13)
V
V
n n s s (24)
t
x
x
Vn Vs
S
(25)
x
s S t
Vs
1 p
T
S
(27)
t
x
x
1 p
T
S
(26)
x x
x
Из (19) и (13)
p
V
V
n n s s (28)
x
t
t
Vn Vs
S T
(29)
t
n x
2 Vn Vs
2S
Из (25)
(30)
x t
s S t 2
2 Vn Vs
S 2T
Из (29)
(31)
2
x t
n x
2 S s S 2 2T
(32)
t 2
n x 2
70.
p Tt p T t T p t
2 2 p 2T
2
2
2
t
p
t
T
p t
T
2 2 p 2T
2
2
2
x
p
x
T
p x
T
2 S S 2 p S 2T
2
2
2
t
p
t
T
p t
T
2 S S 2 p S 2T
2
2
2
x
p
x
T
p x
T
S 2 p S 2T s S 2 2T
2
2
2
p
t
T
t
x
p
n
T
2
2
2
T
p
p
T p t 2 p t 2 x 2
T
71.
xx
p p0 pˆ Re exp i t T T0 Tˆ Re exp i t
a
a
1 1
2 p
x
2
ˆ
i
t
i
exp
p
2
x
a a
a
ˆ
2
x
2
ˆ
i
t
i
exp
T
p
a
T
t 2 p T
p
2
2
ˆ pˆ
ˆ
ˆ
ˆ
p
T
или
p
a
1
a
T 0
p
2
a
T p
T p
T
p T
2 S S 2 s
S
S ˆ s S 2 ˆ
2 S
ˆ
p pˆ T T a 2 T или pˆ a p a T T 0
p
p
T
T
n
n
2 S S 2 s 2
4 S
определитель a
a 1 a
0
n p T
T p p T
T p
72.
22 S S 2 s
0
a 1 a
n
p T T p
p
a1
T
a2 S
s
n S T p
cp
S
T p T
c p p
p
T cv S
c p cv c
p
a1
S
a2 S
sT
nc
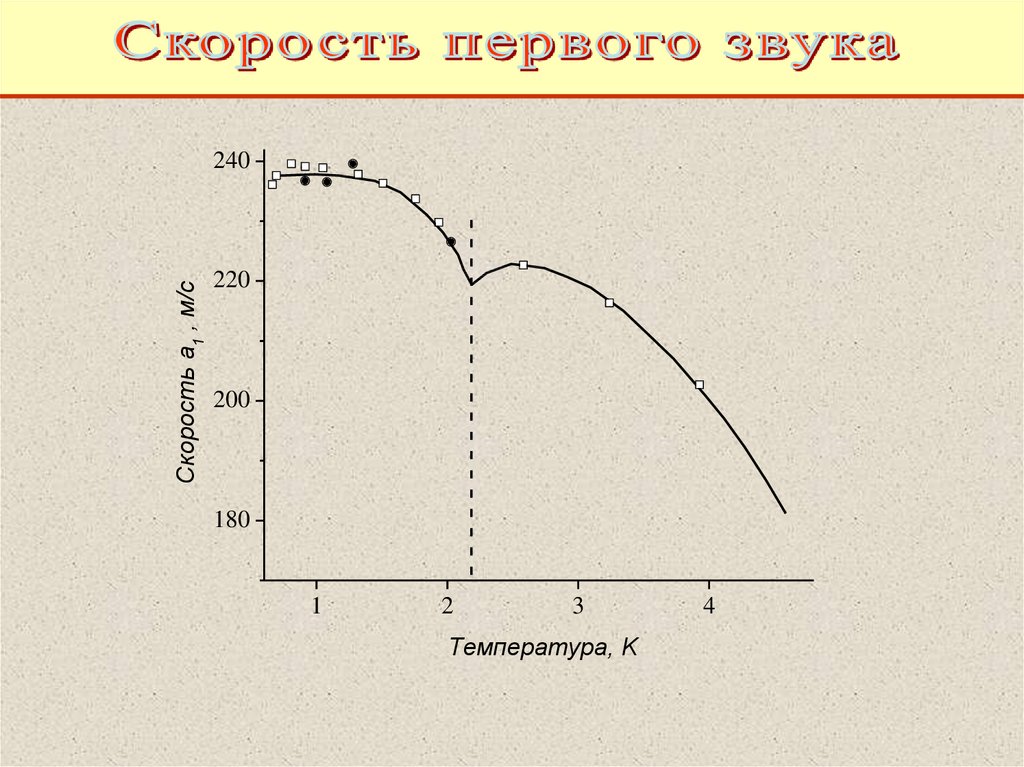
73.
Скорость a1 , м/с240
220
200
180
1
2
3
Температура, K
4
74.
160140
a2, м/сек
120
100
80
60
40
20
0
0.0
0.4
0.8
1.2
T, K
1.6
2.0
2.4
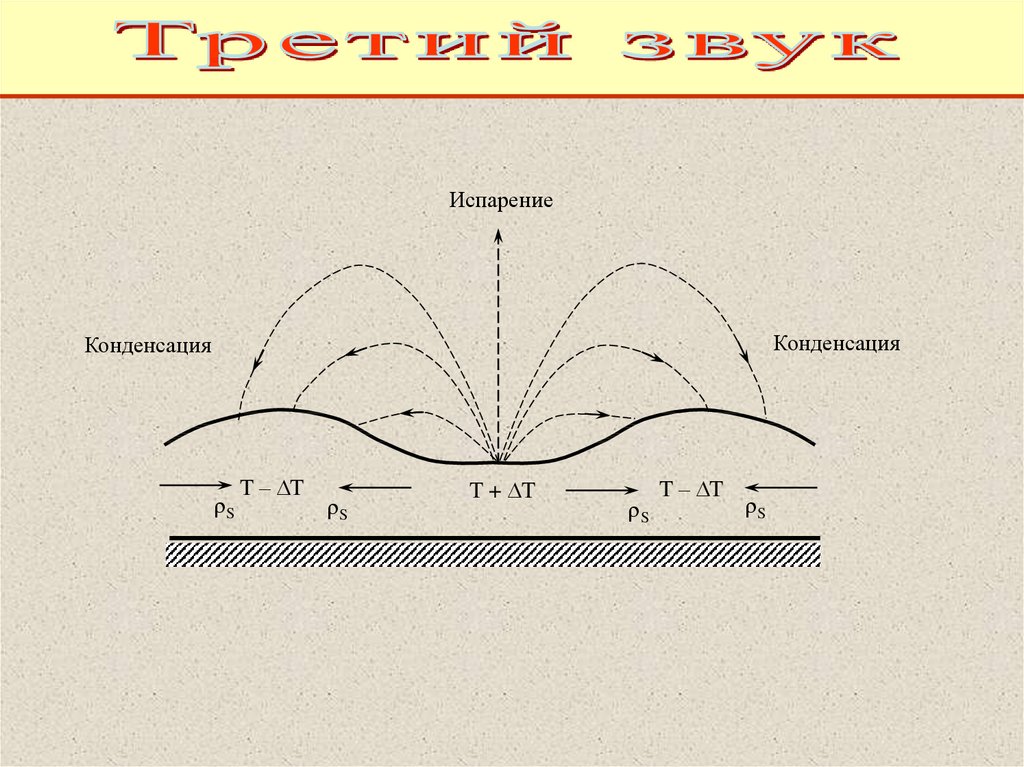
75.
ИспарениеКонденсация
Конденсация
S
T – T
S
T + T
S
T – T
S
76.
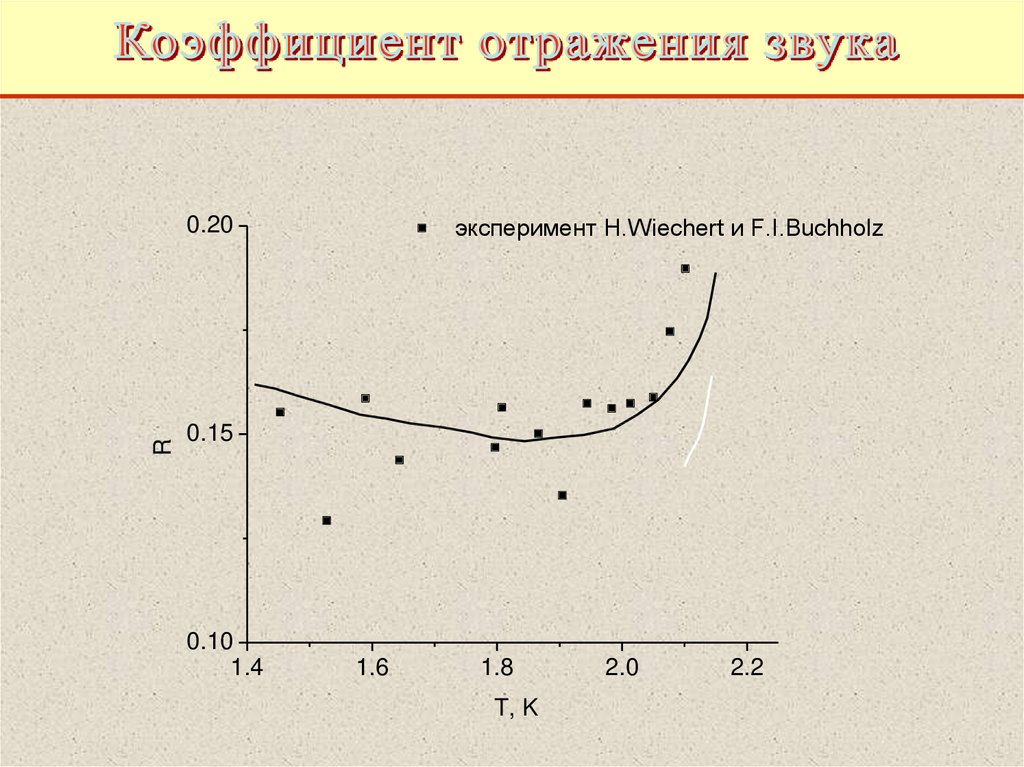
эксперимент H.Wiechert и F.I.BuchholzR
0.20
0.15
0.10
1.4
1.6
1.8
T, K
2.0
2.2
77.
Sdiv SVn 0 (39)
t
S
0
t
divVn 0 (40)
n = const s = const
j nVn sVs
divVs 0 (41)
lk lk p nVnlVnk sVslVsk
nVnl sVsl p nVnlVnk sVslVsk
0 (42)
t
t
xl
xk
xk
DVn
DVs
n
s
p 0 (43)
dt
dt
Vs
Vs2
0 (44)
t
2
Vs2
Vs Vs rotVs Vs
2
Vs
Vs Vs 0 (45)
t
p
rotVs 0
S T
78.
sDVs
s p s S T (46)
dt
DVn
n
n
p s S T (47)
dt
DVs
s
s
p s S T Fвз.тр (46а )
dt
n DVn n p s S T Vn Fвз.тр (47б )
dt
79.
sp s S T 0 (48)
n p s S T Vn 0 (49)
p Vn (50)
При ламинарном нормальном движении
Vn
p1 p2 R 2
8 l
(51)
p S T
2
S T1 T2 R 2
T
T
R
( S )2 TR 2
2
1
2
q STVn ST
( S ) T
T (52)
8 l
8 l
8
C
8
S
2
TR 2
80.
dVsD
n
dVs n
d D
h
m
Vscr
n 1
h 4D
ln
K
(54)
Dm a0
Vscr
1
1 4 (55)
D
Vscr
h
m
h
(53)
Dm
81.
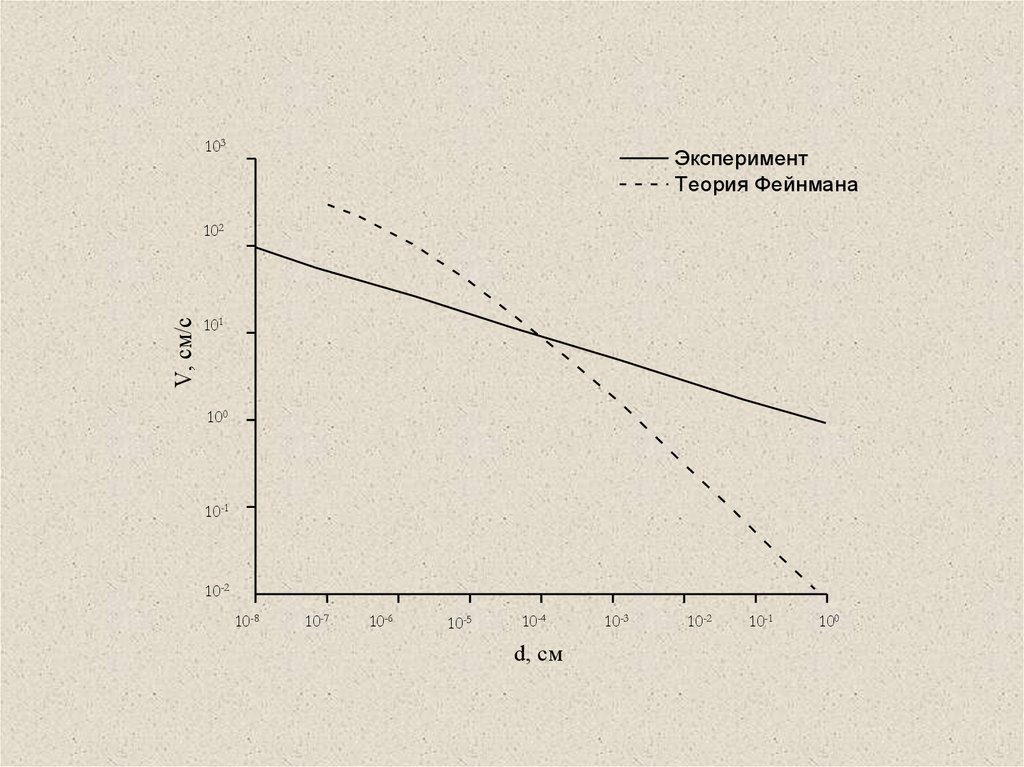
103Эксперимент
Теория Фейнмана
V, см/с
102
101
100
10-1
10-2
10-8
10-7
10-6
10-5
10-4
d, см
10-3
10-2
10-1
100
82.
n sVn Vs
2
2
2
L n Vn Vs
Fвз.тр f L
3000
Параметр Гортера-Меллинка A, м с/кг
f
2500
2000
1500
1000
500
0
1,2
1,4
1,6
1,8
T, K
Fвз.тр A n s Vn Vs
3
(56)
2,0
2,2
83.
s3
p
S
T
A
V
V
0 (57)
s
n s
n
s
n p s S T Vn A n s Vn Vs 3 0 (58)
A V Vs
T n n
S
3
A n 3Vn3
T
S s3
A n 3
T 3 4 3 q f T q3 (59)
s S T
T Cq f T q3 (59a )
84.
5Функция Гортера-Меллинка f, м К/Вт
3
10-9
10-10
10-11
10-12
10-13
10-14
1,2
1,4
1,6
1,8
T, K
2,0
2,2
85.
qqp
А
С
qr
Д
T
86.
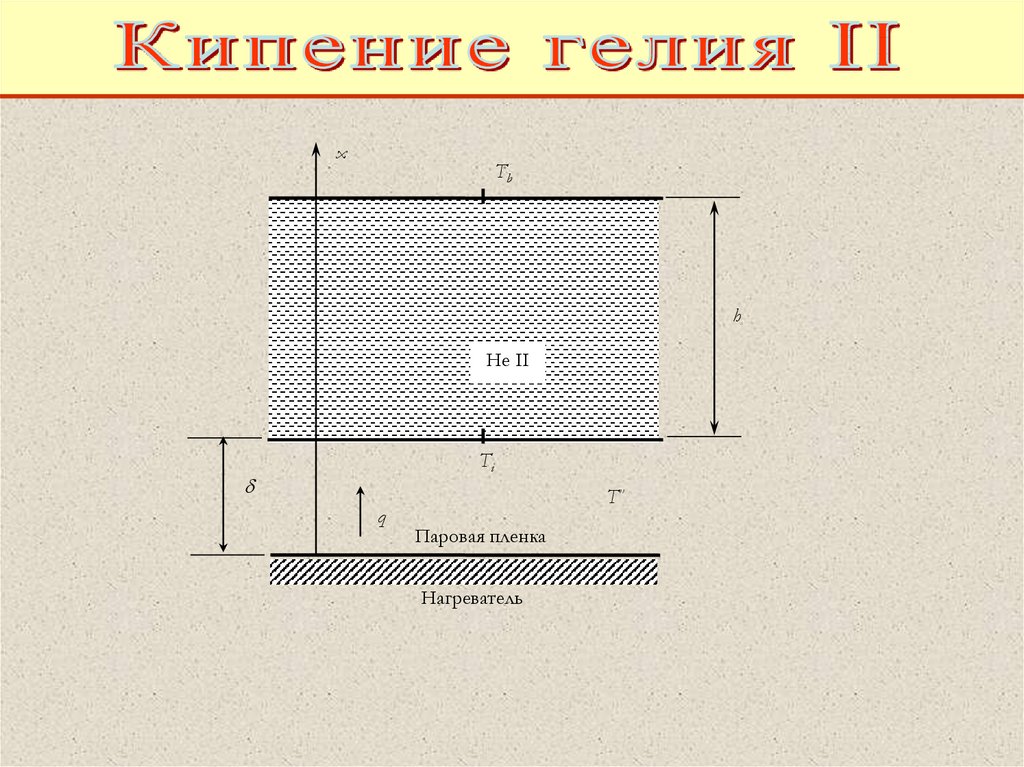
xTb
h
He II
Ti
q
T’’
Паровая пленка
Нагреватель
87.
qR 2,27 p pнас Ti 2RTiq
q~R R
pнас Ti
2 RTi
1
p
RTi
qR 8
1 p
2
pнас Ti
dT
f (T ) q 3
dr
88.
q R rwq
r
qi ri q r
q R 3 rw3
dT
f (T )
dr
r3
T
Ti
Tb
Ti
Ti
dT
dr
3
3
q R rw
3
f T
r
rw
Ti Tb
dT
dT
~
f T
f T
f T
T
b
Ti Tb
~
f T
Ti
dT
f T
T
b
89.
Ti Tb q R 3 rw3q R 3 rw3
q R 3 rw
~
r
2
2
w
2
f T
2r
2rw
q R 3 rw
~
Ti Tb f T
2
p pb gh
T dT
gh
dp
нас.
90.
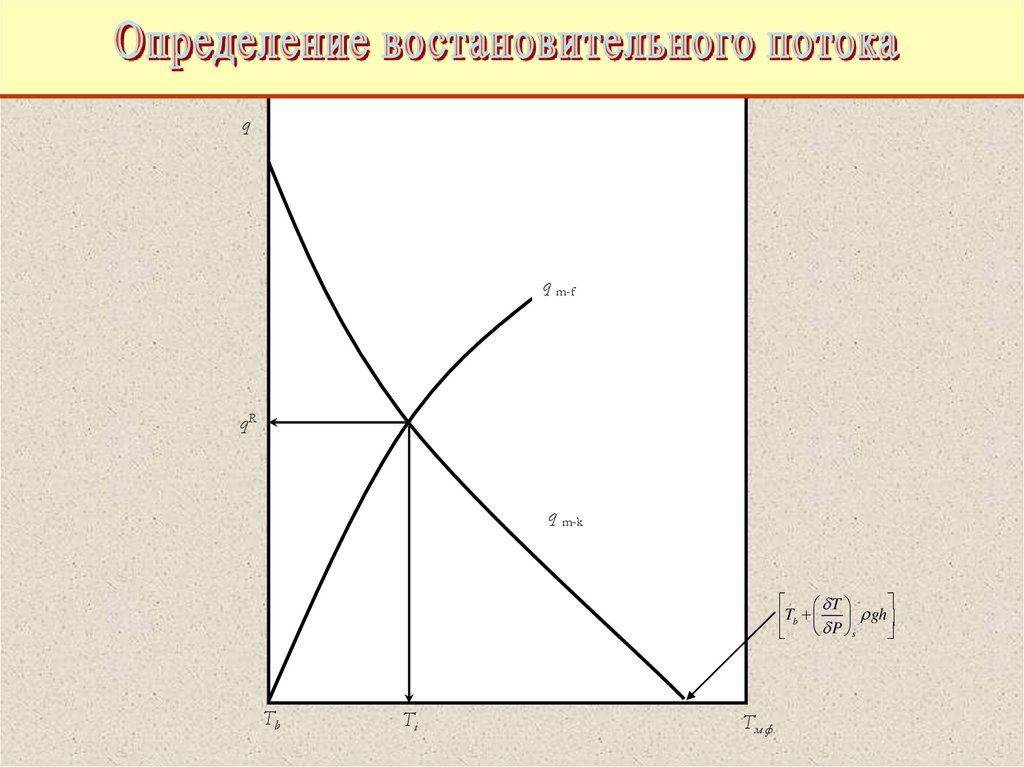
qq m-f
qR
q m-k
T
gh
Tb
P s
Tb
Ti
Tм.ф.
91.
P”Пар
q
Ti0
I
l
II
Жидкая перемычка
III
Ti Pb”
Пар
Стенки капилляра
Нагреватель
j
d
92.
93.
94.
95.
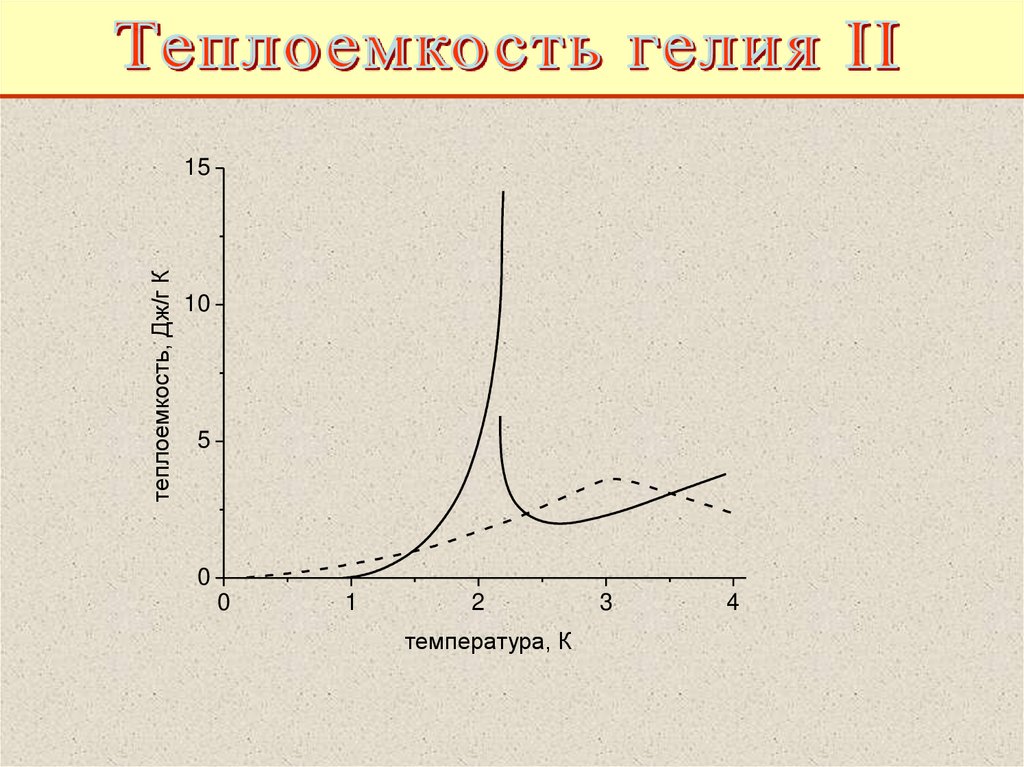
теплоемкость, Дж/г К15
10
5
0
0
1
2
температура, К
3
4
96.
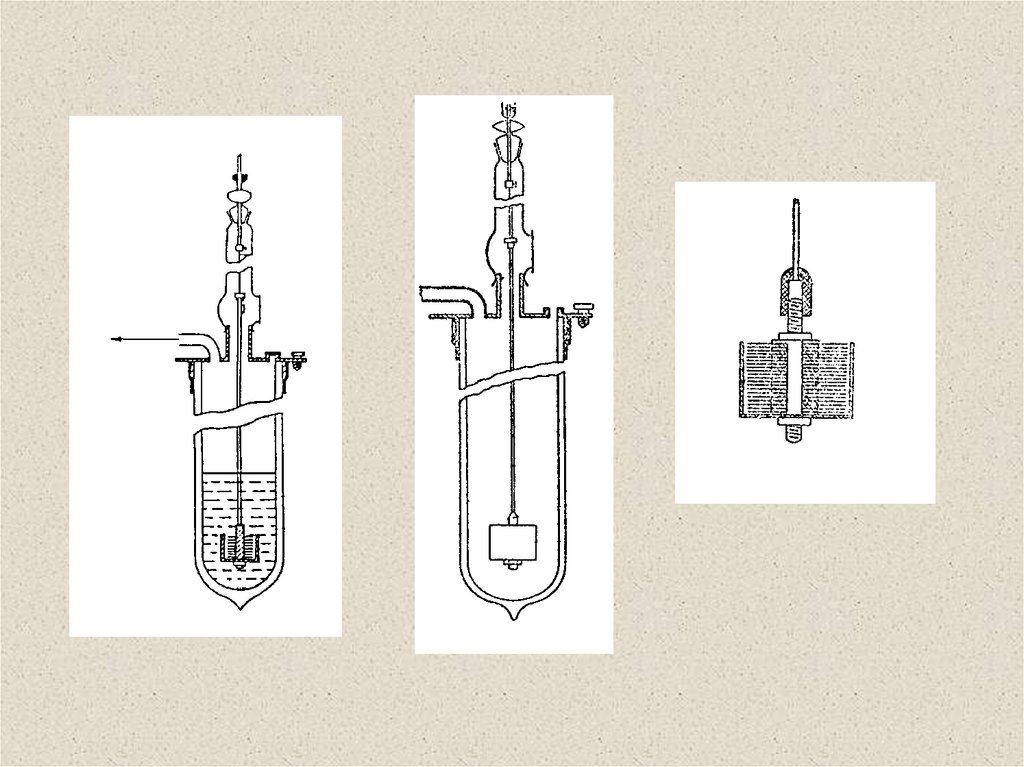
1.0второй звук
крутильный вискозиметр
0.8
n/
0.6
0.4
0.2
0.0
1.2
1.6
2.0
T (K)




































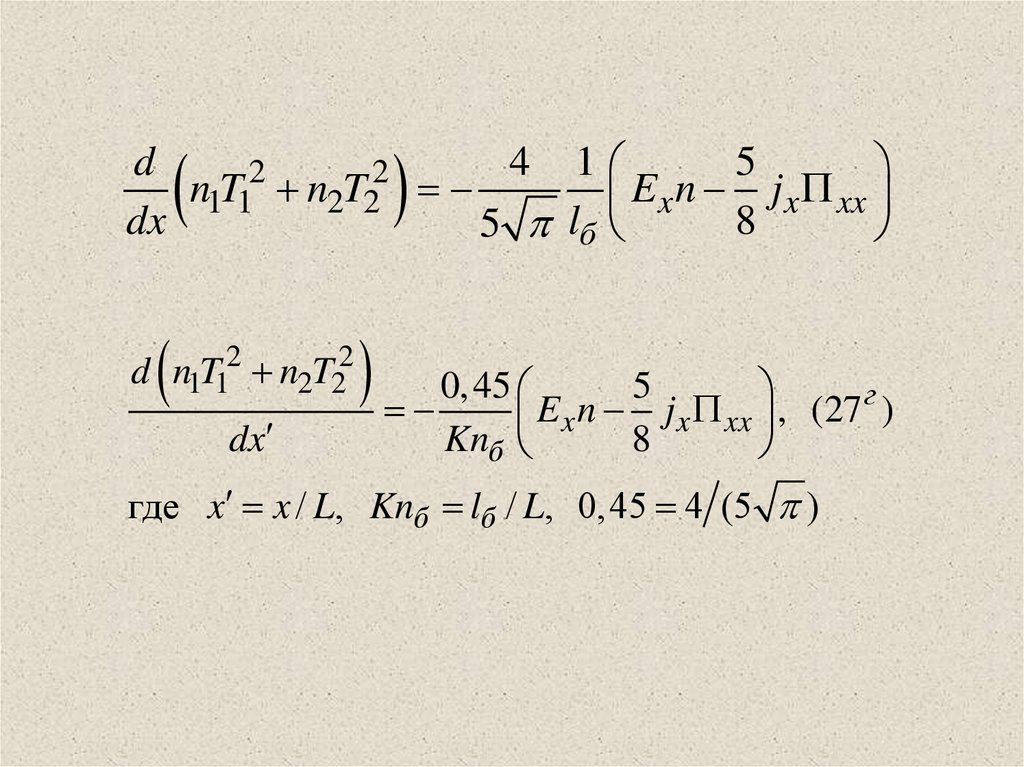










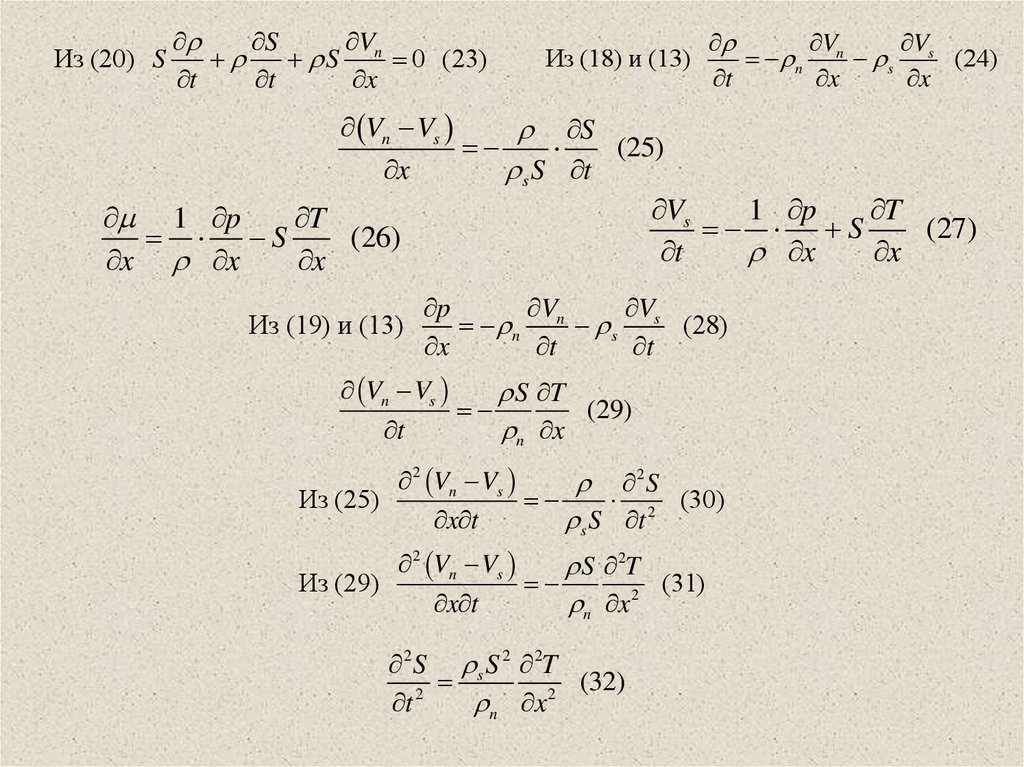
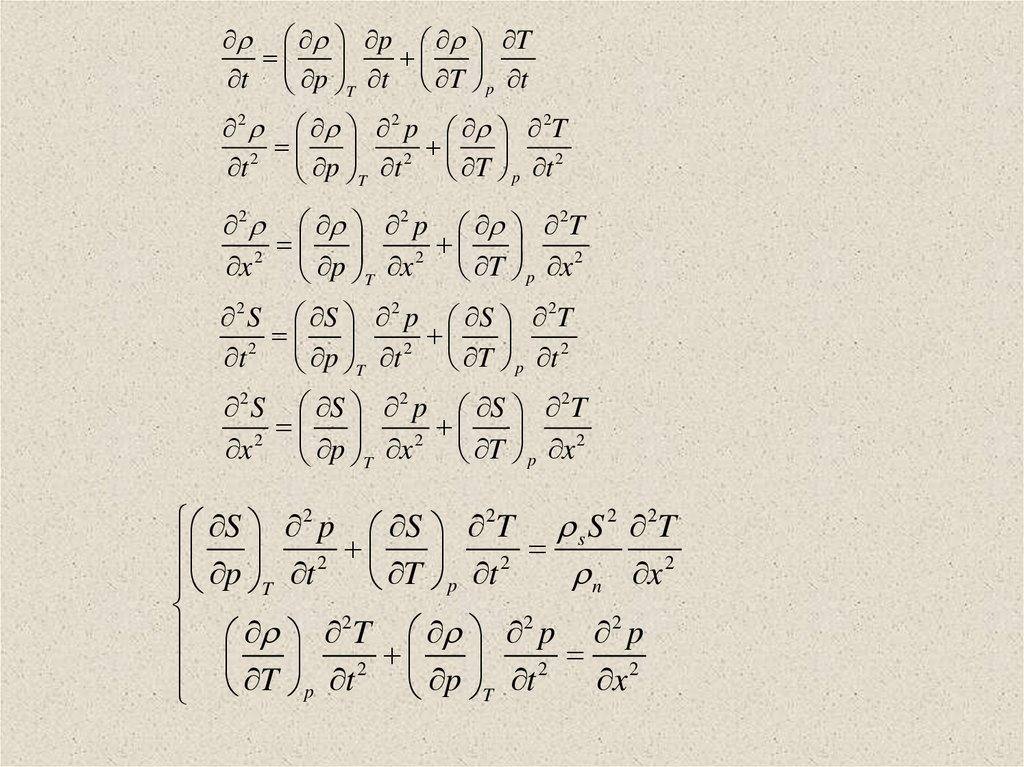
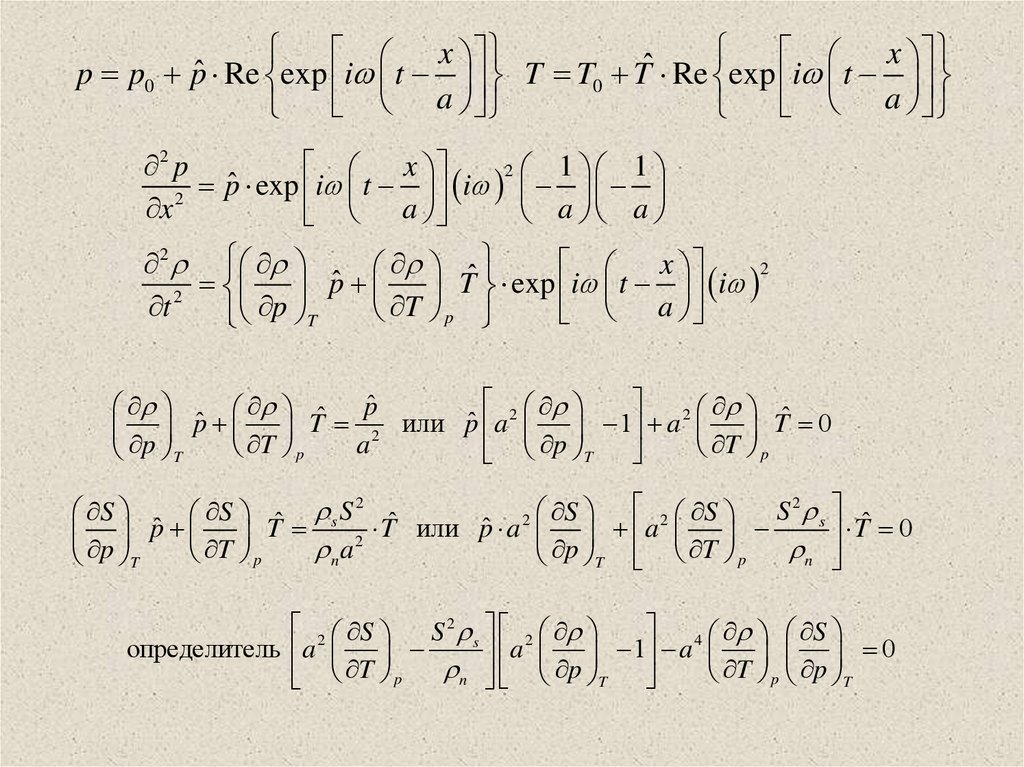
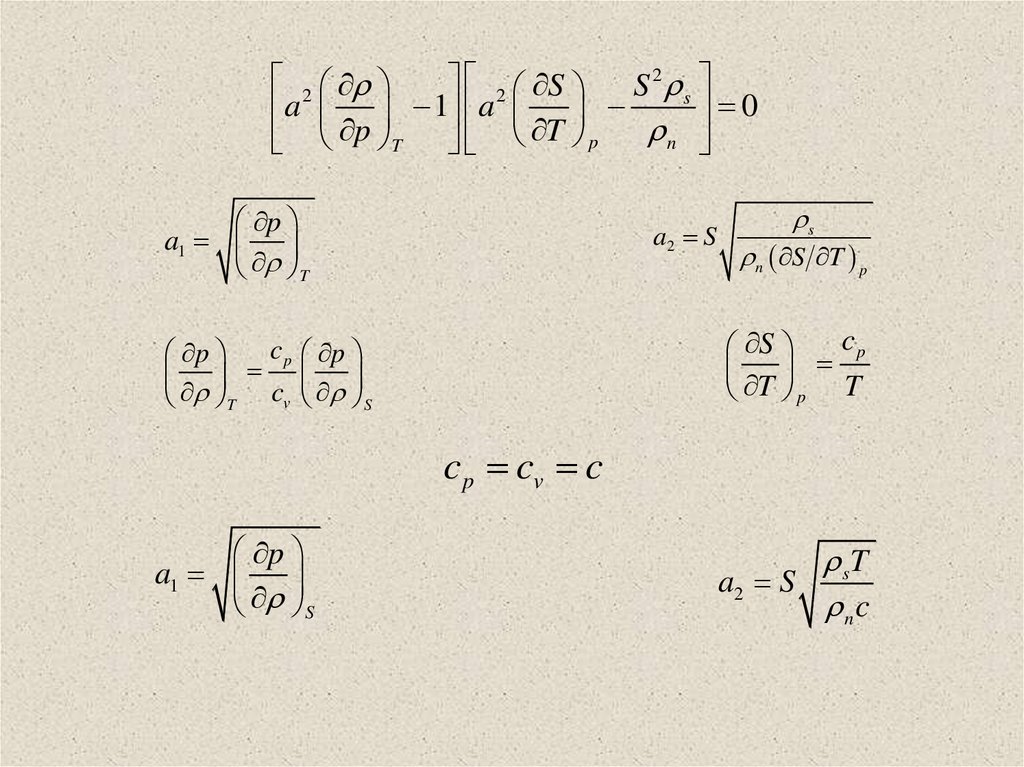










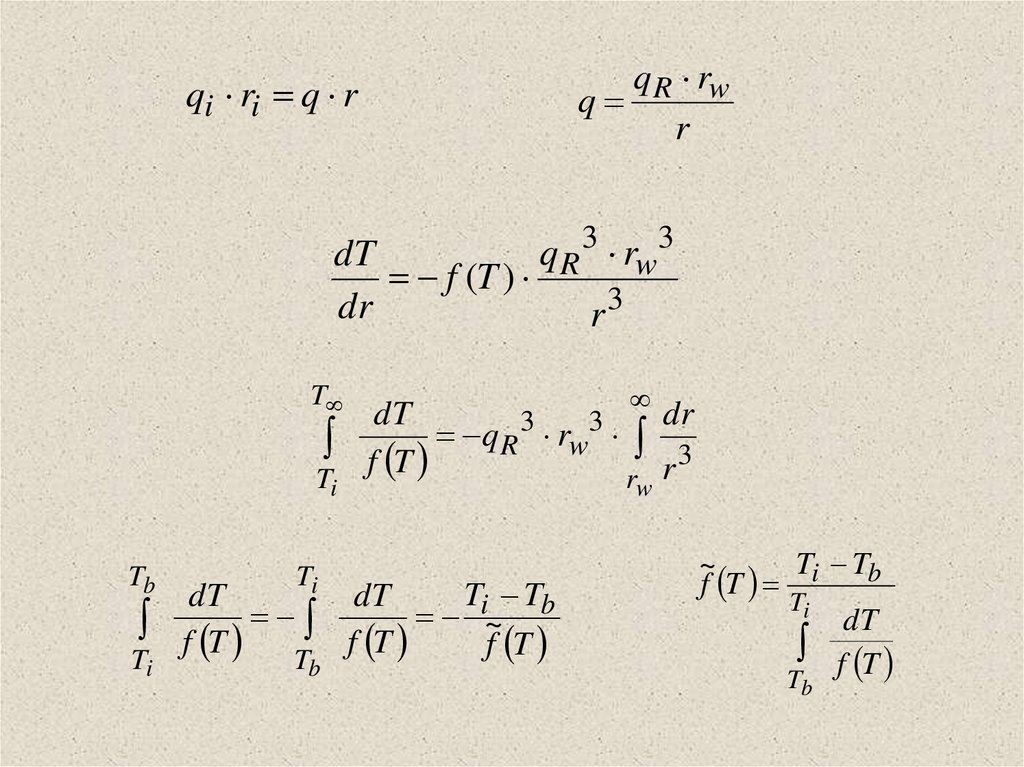
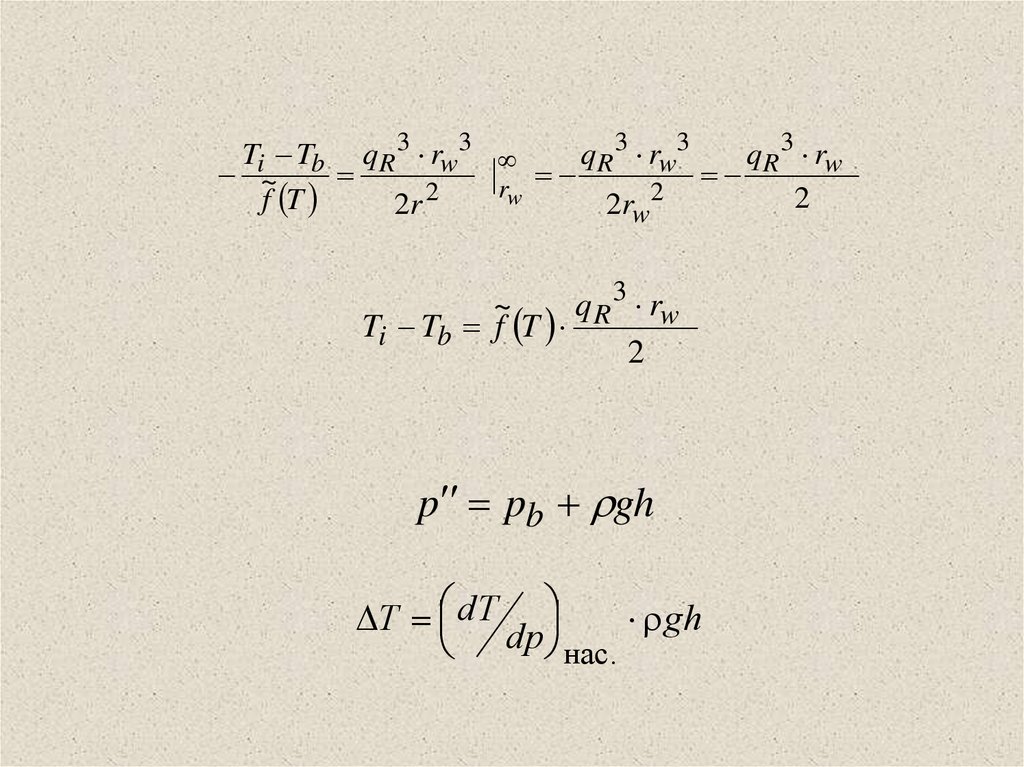



 Физика
Физика








