Похожие презентации:
Матрицалар және оларға қолданылатын амалдар
1. Математика 1 №1 ДӘРІС Матрицалар және оларға қолданылатын амалдар. Анықтауыштар. Ибраимова А.К., проф.асситенті
2. ЖОСПАР: 1. Матрица түсінігі 2. Матрица түрлері 3. Матрицаларға қолданылатын амалдар. 4. 2-ші және 3- ші ретті анықтауыштар. 5.
Минор, алгебралық толықтауыштар.3.
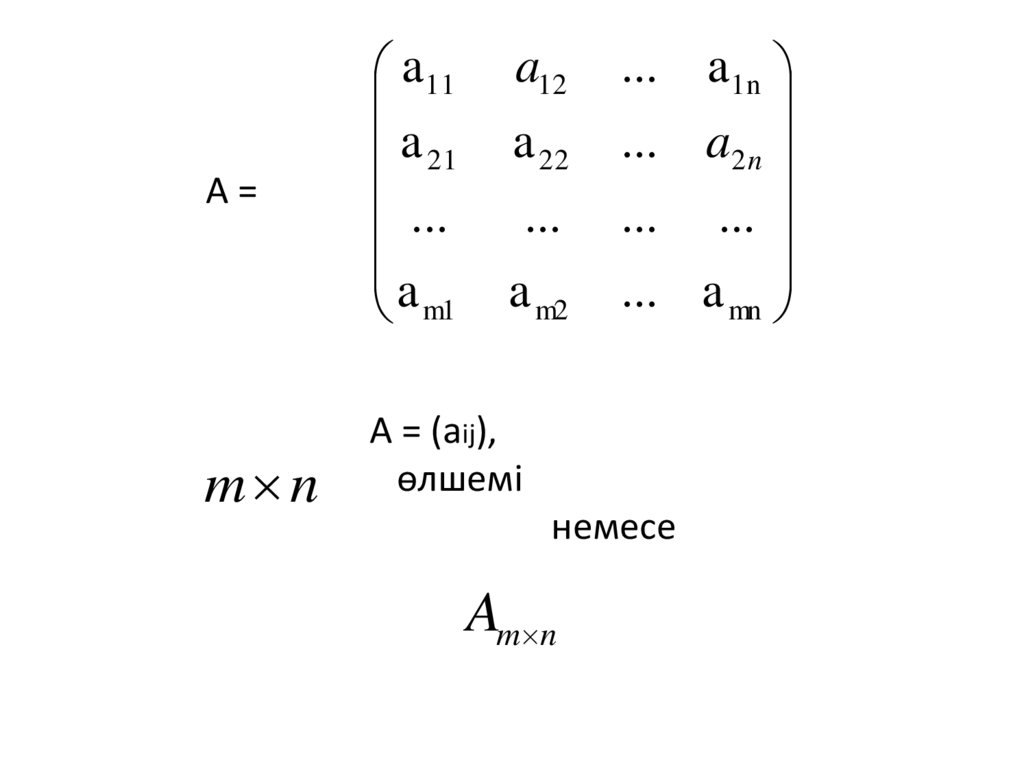
Анықтама:mхn өлшемді матрица деп, m жол
мен n бағаннан тұратын сандардың тік
бұрышты кестесін айтады.
Матрицаны құрайтын сандарды
матрица элементтері деп атайды,
матрицаны латынның бас әріптерімен А,
В, С, ... белгілейді.
4.
А=m n
a11
a 21
...
a
m1
a12
a 22
...
a m2
... a1n
... a2 n
... ...
... a mn
А = (аij),
өлшемі
немесе
Am n
5. Матрицалардың түрлері:
• үшбұрышты1
0
А
0
0
• Нөлдік матрица - О:
2 5 3
4 7 2
0 3 4
0 0 8
6.
Диагоналдық матрица
• Бірлік матрица
1
0
E
0
0
0 0 0
1 0 0
0 1 0
0 0 1
жолды матрица және бағанды матрица
A a1 a2
b1
... am , B b2
b
n
7. Анықтама: А матрицадағы жол мен сәйкес бағанды алмастырғанда пайда болған матрицаны алмастырылған матрица деп атайды. А матрица
өлшемі mxn болса, алмастырылғанматрицаның
өлшемі
nxm
болады.
• Мысалы:
егер
, оңда
8.
Матрицаларға қолдану амалдарматрицаны санға көбейту, қосу, азайту, көбейту,
матрицаларды дәрежеге шығару.
1.
,
B A
1 2 3 5 10 15
 5
4 5 6 20 25 30
2.
1 2 3 0 1 2 1 3 5
C=A+B, С=
4 5 6 3 4 5 7 9 11
3.
А-В=A+(-1)B
9.
• Қасиеттері:а) коммутативтік A+B=B+A,
б) ассоциативтік (A+B)+C=A+(B+C)
в) дистрибутивтік (A+B)= A+ B.
4.
AB a 1
cij ai1b1 j ai 2 b2 j ... aik bkj
a2
b1
n
b2
a n a1b1 a2b2 anbn a i b i
i 1
b
n
10.
• Қасиеттері:а) ассоциативтік A (BC)=(AB) C;
б) дистрибутивтік A (B+C)=AB+AC
және
(B+C) A=BA+CA.
• Квадраттық матрицаларға AB = A B
11.
• Мысалы:4
1) С 1 2. 3 5 1 4 2 5 3 6 32
6
2)
1 2
A
3 4
Табу керек AB және BA.
0 1
B
2 3
12.
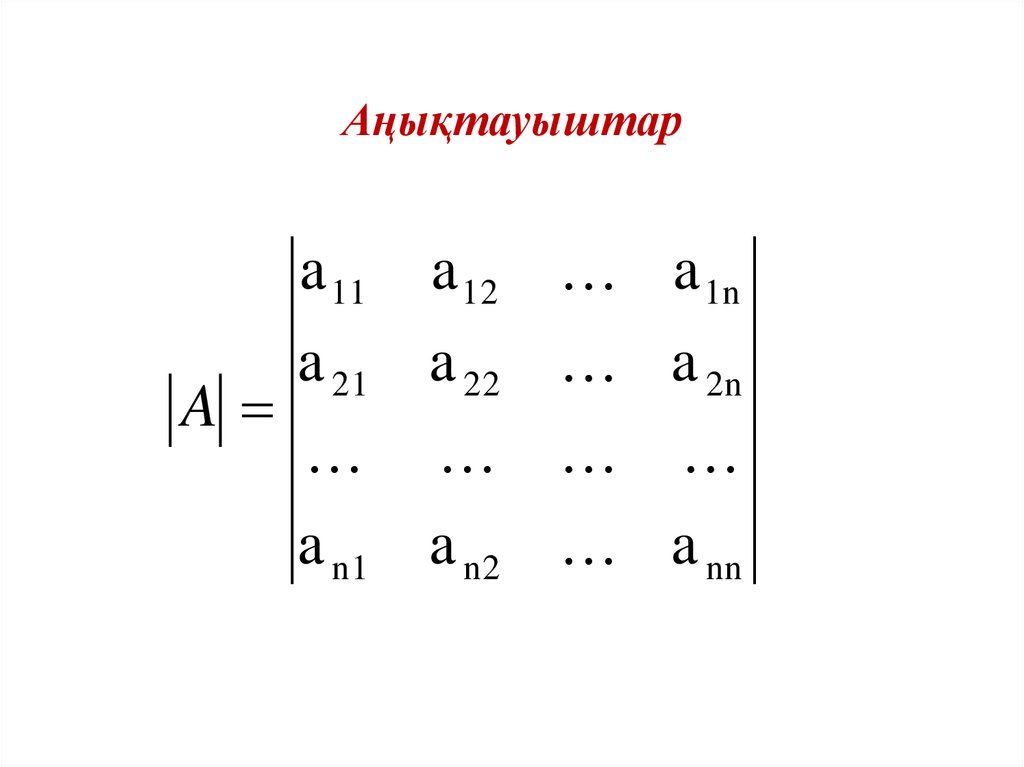
Аңықтауыштарa 11
A
a 12 a 1n
a 21 a 22 a 2n
a n1 a n2 a nn
13.
2-ші ретті анықтауыш
Анықтама: 4 саннан тұратын квадрат
кесте 2-ші ретті анықтауыш деп аталады
да, - деп белгіленеді:
a 11 a 12
a 11a 22 a 12a 21
a 21 a 22
Мысалы:
1 2
3 4
1 4 2 3 2
14.
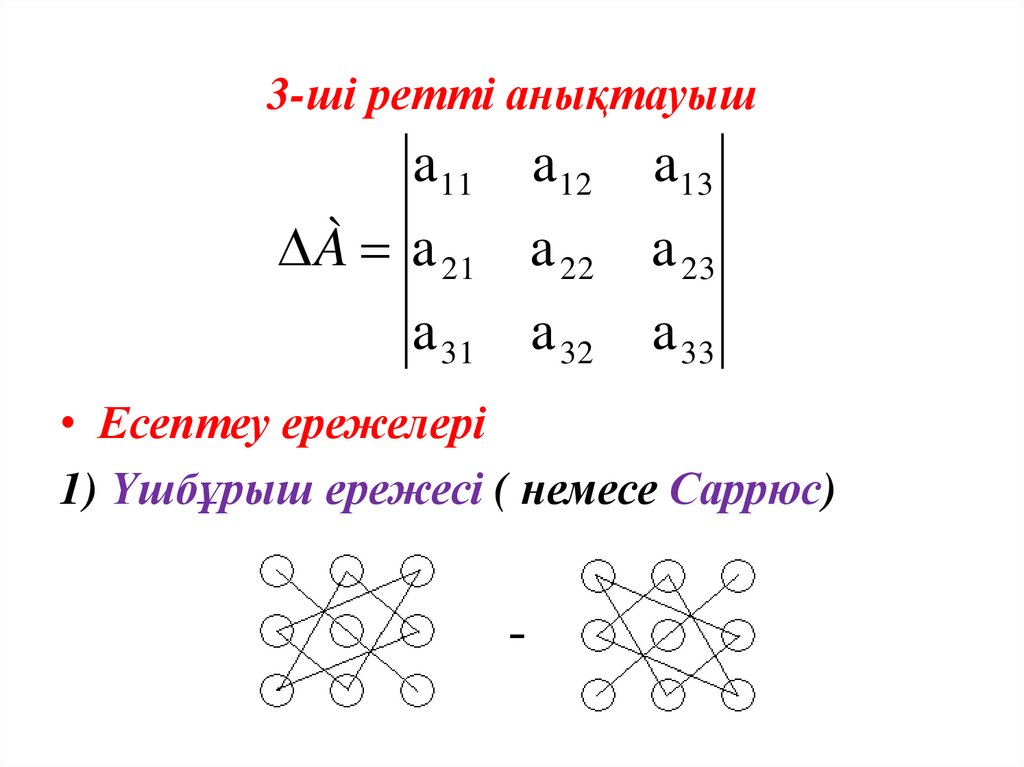
3-ші ретті анықтауышa 11
a 12
a 13
À a 21 a 22
a 23
a 31 a 32
a 33
• Есептеу ережелері
1) Үшбұрыш ережесі ( немесе Саррюс)
-
15.
a 11a 12
À a 21 a 22
a 31 a 32
a 13
a 23
a 33
a11a22a33 a12a23a31 a13a21a32
a13a22a31 a11a23a32 a12a21a33
16.
Мысалы:1 2 3
4 5 6 1 5 9 2 6 7 3 4 8 3 5 7 2 9 4 1 6 8 0
7 8 9
17.
Минорn-ші ретті анықтауыш берілген болсын .
Анықтама: a ij элементінің M ij миноры деп ,
қиылысында осы элемент тұрған жол мен бағанды
сызып тастағанда пайда болған (n-1) ретті жаңа
анықтауышты айтады.
a11 a12 a13
Мысалы: M 12
a 21 a 22 a 23
a 31 a 32 a 33
a21 a23
=a
31
a33
a21a33 a31a23
18.
Анықтама: a ij элементінің Aij -алгебралықтолықтауышы деп 1 таңбасымен алынған
i j
A
оның минорын айтады: ij = 1 M ij .
i j
Мысалы:
A23 1
2 3
M 23 M 23 .
19.
• Мысалы:1 2
A
3 4
A11=(–1) 1+1 4=4, A12=(–1) 1+2 3= –3
A21=(–1) 2+1 2= –2, A22=(–1) 2+2 1=1
Қосалқы матрица
A 11 A 12
~ A 21 A 22
A
A n1 A n2
A 1n
A 2n
A nn
20.
СӨЖ тапсырмасы• 1. n-ші ретті анықтауыштар. Қасиеттері
[2] -21б.
• жүт-1.1 [1-43 б.]
(Өткізу мерзімі график бойынша)
ОСӨЖ тапсырмасы
• 1. n-ші ретті анықтауышты жіктеу [3] 7б.
21.
Бақылау сұрақтары:1. Матрица, түрлері, оларға
қолданылатын амалдар.
2. Анықтауыштар, оларды есептеу.
3. Минор, алгебралық
толықтауыштар.
22. ТЕСТ СҰРАҚТАРЫ
1. Анықтауышты есептеңіз:А) 8
В) -4
3
2
1
2
1
3
2
0
2
С) -12
Д) 2
2 х 4
2. Теңдеуді шешіңіз: 1 х 0
А)10
В) -4
С) 12
Д) -6
3. Берілген А матрицасының а элементінің алгебралық
22
толықтауышын табыңыз: А =
А)-2
В) -1
С) 2
3 2 1
5 8 9 .
2 1 1
Д) 1
23.
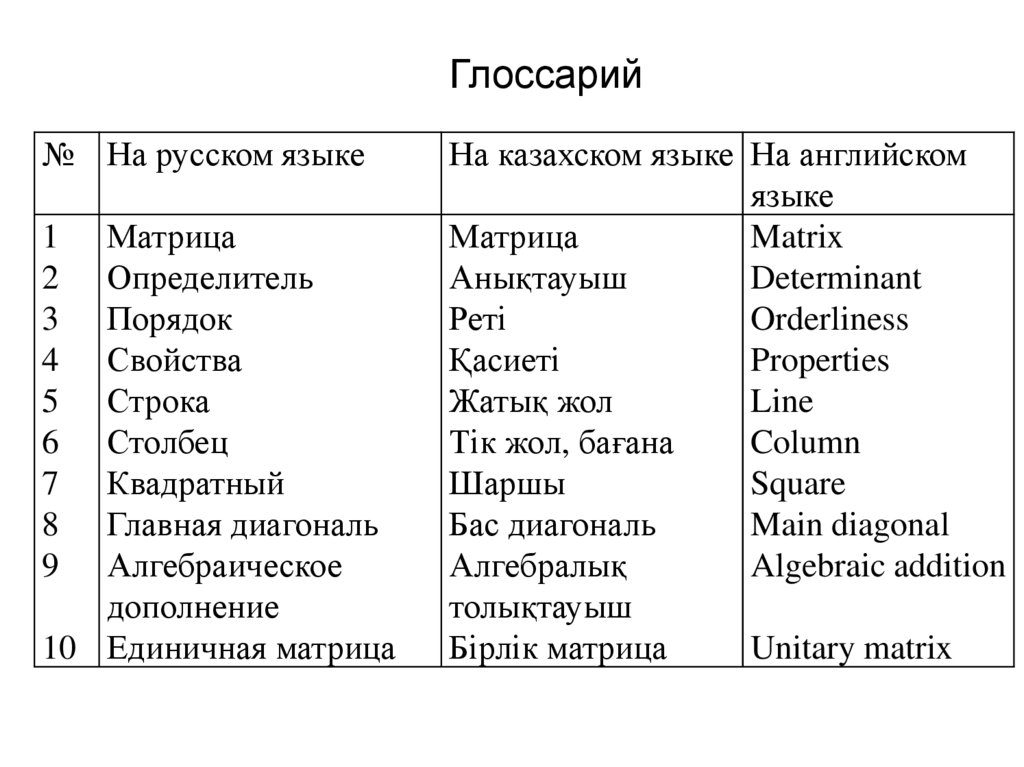
Глоссарий№ На русском языке
Матрица
Определитель
Порядок
Свойства
Строка
Столбец
Квадратный
Главная диагональ
Алгебраическое
дополнение
10 Единичная матрица
1
2
3
4
5
6
7
8
9
На казахском языке На английском
языке
Матрица
Matrix
Анықтауыш
Determinant
Реті
Orderliness
Қасиеті
Properties
Жатық жол
Line
Тік жол, бағана
Column
Шаршы
Square
Бас диагональ
Main diagonal
Алгебралық
Algebraic addition
толықтауыш
Бірлік матрица
Unitary matrix
24.
Әдебиет тізіміНегізгі:
1. Айдос Е. Ж. Жоғары математика 1. Алматы . 2007,
2. Мустахишев К.М. Математика 1,2 Оқулық . 2007
3. Крофт Э., Дэвисон Р. Математика негіздері.1 бөлім Оқулық
- Алматы: ҚР ЖОО Қауымдастығы, 2013.
4. Сыдыкова Д.К., « Математика I пәнінің курсы» 1,2
Модуль, қашықтан оқыту үшін арналған электрондық
оқулық. -Алматы, КазБСҚА , - 2012
Қосымша:
5. Хасеинов К.А. Математика канондары. Жоғары математика
курсы. Алматы: Атамұра,2011.
6. Сыдыкова Д.K. Математика 1. Студенттердің жеке
тапсырмаларын орындауға арналған әдістемелік нұсқау. Алматы: КазГАСА, 2008.
7. Қабдықайыр Қ. Жоғары математика. Алматы: Дәуір, 2005.











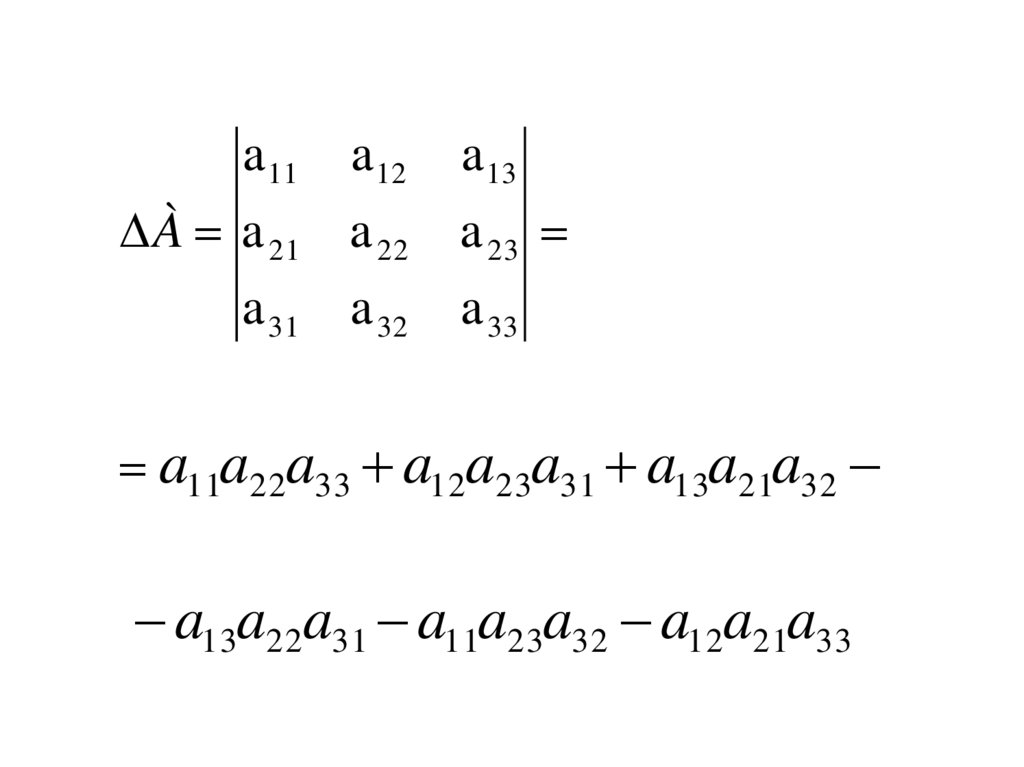








 Математика
Математика








