Матрицалар және оларға амалдар қолдану

1.

Сабақ жоспары
Мамандығы:
Пәні: Алгебра, ЭЕМ – де есептеу әдістері
Оқыту түрі мен формасы: Дәстүрлі емес.
Сабақтың типі: Жаңа сабақты хабарлау.
Сабақтың түрі: Бинарлық сабақ.
Сабақтың әдісі: Репродуктивті, түсіндірмелі-иллюстративті, топтық оқыту, визуальды лекция.
Сабақтың тақырыбы: Матрицалар және оларға амалдар қолдану.
Сабақтың мақсаттары:
Білімділік мақсаты:
а) Матрицаларға анықтама беру және оларға қолданылатын қосу, азайту, матрицаны санға,
матрицаны матрицаға көбейту амалдарымен таныстыру.
ә) Матрицаларға амалдар қолдануда MS Excell программасындағы қосынды, көбейтінді, яғни
МУМНОЖ функциясының атқаратын қызметімен таныстыру.
Тәрбиелік мақсаты: Студенттердің шығармашылық білігін, танымдық қабілетін арттырып,
тұжырым жасай білуге,
ой пікірін дәлелдеуге және программалық сауатталыққа тәрбиелеу.
Дамытушылық мақсаты: Студенттердің логикалық ойлауын, салыстыру, ажырату дағдыларын
дамыту, ақпараттық
дүниетанымым кеңейту, әрекеті бойынша жұмысты қалыптастыру, талдау және алынған
білімді пайдалану.
Міндеті: а) Студенттерді шапшаңдыққ өз ойын ашық айта білуге,
ә) ұжымдық ауызбіршілікке шақыру,
б) топта жұмыс істеуге баулу,
в) дүниетаным шеңберін кеңейту.
Пәнаралық байланыс: Алгебра және ЭЕМ-де есептеу әдістері.
Сабақтың көрнекілігі:
Лекция топтамасы, Интерактивті тақта, слайдтар, компьютерлер.
Қолданылатын әдебиеттер тізімі: В.Т.Лисичкин,.ИЛ.Соловейчик «Математика», Москва, 1991ж.
Н.Ермеков. «Ақпараттық технологиялар». Астана. 2007 ж.

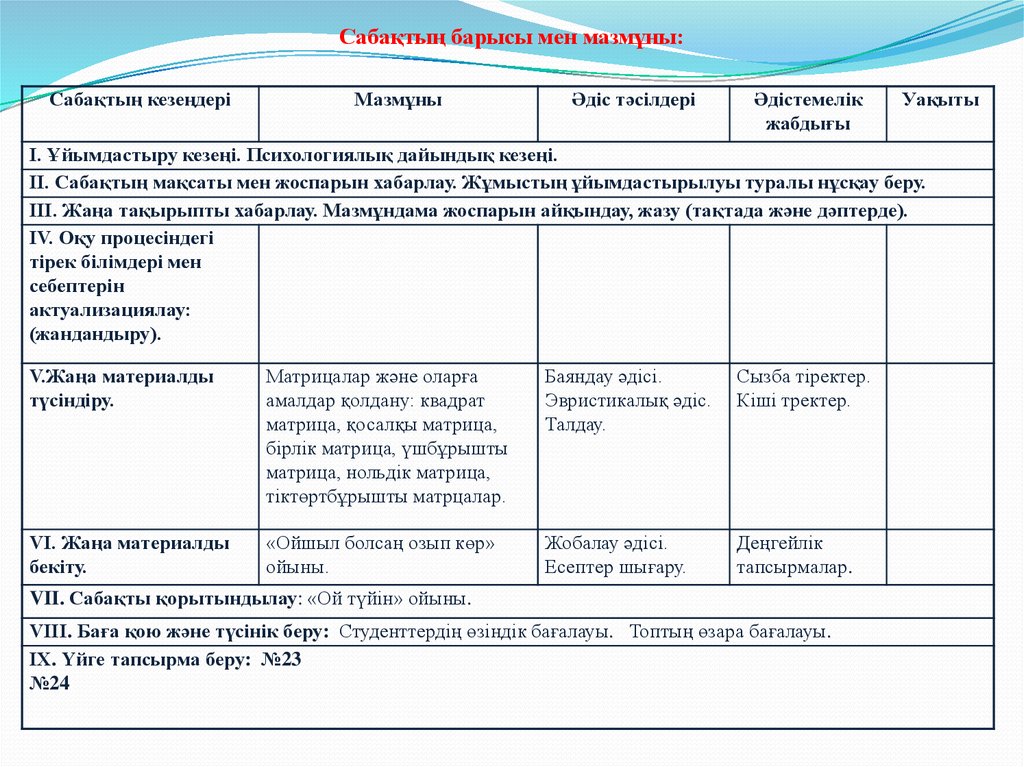
2. Сабақтың барысы мен мазмұны:

Сабақтың кезеңдері
Мазмұны
Әдіс тәсілдері
Әдістемелік
жабдығы
Уақыты
І. Ұйымдастыру кезеңі. Психологиялық дайындық кезеңі.
ІІ. Сабақтың мақсаты мен жоспарын хабарлау. Жұмыстың ұйымдастырылуы туралы нұсқау беру.
ІІІ. Жаңа тақырыпты хабарлау. Мазмұндама жоспарын айқындау, жазу (тақтада және дәптерде).
ІV. Оқу процесіндегі
тірек білімдері мен
себептерін
актуализациялау:
(жандандыру).
V.Жаңа материалды
түсіндіру.
Матрицалар және оларға
амалдар қолдану: квадрат
матрица, қосалқы матрица,
бірлік матрица, үшбұрышты
матрица, нольдік матрица,
тіктөртбұрышты матрцалар.
Баяндау әдісі.
Эвристикалық әдіс.
Талдау.
Сызба тіректер.
Кіші тректер.
VI. Жаңа материалды
бекіту.
«Ойшыл болсаң озып көр»
ойыны.
Жобалау әдісі.
Есептер шығару.
Деңгейлік
тапсырмалар.
VII. Сабақты қорытындылау: «Ой түйін» ойыны.
VІІІ. Баға қою және түсінік беру: Студенттердің өзіндік бағалауы. Топтың өзара бағалауы.
ІX. Үйге тапсырма беру: №23
№24

3. Ұйымдастыру кезеңі. Аудиторияның тазалығына көңіл бөлеміз. Студенттердің сабаққа дайындығын тексеру.   Пән: ЭЕМ-де есептеу

Ұйымдастыру кезеңі.
Аудиторияның тазалығына көңіл бөлеміз.
Студенттердің сабаққа дайындығын тексеру.
Пән: ЭЕМ-де есептеу әдістері.
«Қазіргі заманда жастарға ақпараттық технологиямен байланысты әлемдік стандартқа сай мүдделі жаңа
білім беру өте қажет».
Н. Ә. Назарбаев.
Пән: Алгебра.
Дүниенің сәнін екі нәрсе келтіреді:
1) Математикамен шұғылдану,
2) Одан сабақ беру.
С. Д. Пуассон.
Жаңа сабақты түсіндіру.
Пән: Алгебра. Жүсіпбекова М.У.
m n ретті матрица деп- m-жатық, n-тік жолдардан анықталған тік бұрышты таблицаны айтады.
a11 a12 a1n
A
a 21 a 22 a 2 n
....................
a m1 a m 2 a mn
A aij , i 1, m,
j 1, n
a ij - матрицаның элементі деп аталады.

4.

Бірінші индекс і матрицаның жатық жолының, екінші индекс j матрицаның тік жолының нөмірін
анықтайды.
Егер матрицаның тік жолының саны жатық жолының санына тең болмаса, онда ол матрица тікбұрышты
матрица деп аталады.
a11 a12 a13
A
a21 a22 a23
a31 a32 a33
a41 a42 a43
Егер матрицаның жатық жолының саны тік жолының санына тең болса, онда матрица квадратты
матрица деп аталады.
a11 a12 a1n
A a 21 a 22 a 2 n
a31 a32 a33
Енді n-ретті квадратты матрицаны қарастырайық.
a11 a12 ......a1n
A
a 21 a 22 ......a 2 n
..........................
a m1 a m 2 .....a mn
Бұл жағдайда А матрицасы n-ретті квадратты матрица деп аталады.
Квадратты матрицаның a11 , a22 ......ann элементтері оның негізгі диагоналы деп аталады.
a1n , a 2 n 1 ,......a n1
элементтері қосалқы диагоналы деп аталады.

5.

Кез-келген бір санды бір жатық немесе бір тік жолдан тұратын матрица деп қарастыруға болады және оның реті 1 x 1
болады. Егер матрицаның барлық элементтері 0-ге тең болса, онда ол матрица нөл матрица деп аталады.
0 0 0.....0
A
0 0 0.....0
.................
0..............0
Егер матрицаның негізгі диагоналының элементтерінен өзге элементтері нөлге тең болса, онда матрица
диагоналды матрица деп аталады.
a11 0 0
A 0 a 22 0
0 0 a33
Егер диагоналды матрицаның барлық элементтері 1-ге тең болса, онда матрица бірлік матрица деп аталады.
1 0 0
A 0 1 0
0
0 1

6. Егер негізгі диагоналдан төмен немесе жоғары орналасқан элементтері 0-ге тең болса, онда квадратты матрица үшбұрышты матрица

деп аталады.
a11 a12 a1n
A 0
0
a11 0
A a 21 a 22 0
a 22 a 2 n
0
0
a31 a32 a33
a33
Егер матрица бір жатық (тік) жолдан анықталса, онда матрица жатық (тік) жолды матрица деп аталады.
a11
B a11 a12 .... a1n
A a 21
a31
Берілген квадрат А матрицасының анықтауышы немесе детерминанты мына түрде беріледі:
a11 a12 ......a1n
A
a 21 a 22 ......a 2 n
..........................
a m1 a m 2 .....a mn
Бірлік Е матрицасының анықтауышы 1-ге тең, яғни
E 1

7.

Матрицаларға амалдар қолдану
а) Матрицалардың алгебралық қосындысы
Матрицаларға қосу, азайту, көбейту және матрицаға санды көбейту амалдары қолданылады. Бірақ осы
аталған амалдар кез-келген матрицаға орындалмайды.
1. Матрицаларды қосу.
Бірдей ретті A aij , B bij матрицаларының алгебралық қосындысы деп-сол ретті C cij
матрицасын айтамыз.
C A B
және оның кез-келген элементтері мына формуладан анықталады:
C aij bij
Мысалы,
m n
i 1, m, j 1, n
ретті А мен В матрицаларының алгебралық қосындысын қарастырайық.
a11 a12 ...a1n b11 b12 ...b1n a11 b11 a12 b12 .....a1n b1n
C A B .................. .................. .............................................
a
a
a
b
b
b
a
b
a
b
a
b
m
1
m
2
.....
mn
m
1
m
2
.....
mn
m
1
m
1
m
2
m
2
......
mn
mn
Демек, матрицалардың алгебралық қосындысының формуласынан мынадай қорытындыға келеміз.
Бірдей ретті матрицалардың алгебралық қосындысына нақты сандарға орындалатын ауыстырымдылық пен
терімділік қасиеттер орындалады.
1) Ауыстырымдылық қасиет: А+В=В+А
2) Терімділік қасиет:
(А+В)+С=А+(В+С)
3) А+0=А
4) А+(-А)=0

8. Мысал №1

2 4
,
A
1
3
1 3
B
1
4
C ?
2 4 1 3 2 ( 1) 4 3 1 7
C A B
1
3
1
4
(
1
)
1
3
(
4
)
0
1
Мысал №2
2 1
1 0 3
A 3 5 , B
2 4 8
0 8
Бұл матрицаларды қоса алмаймыз.
Ескерту: Тек бірдей ретті матрицаларда ғана қосу амалы орындалады.

9.

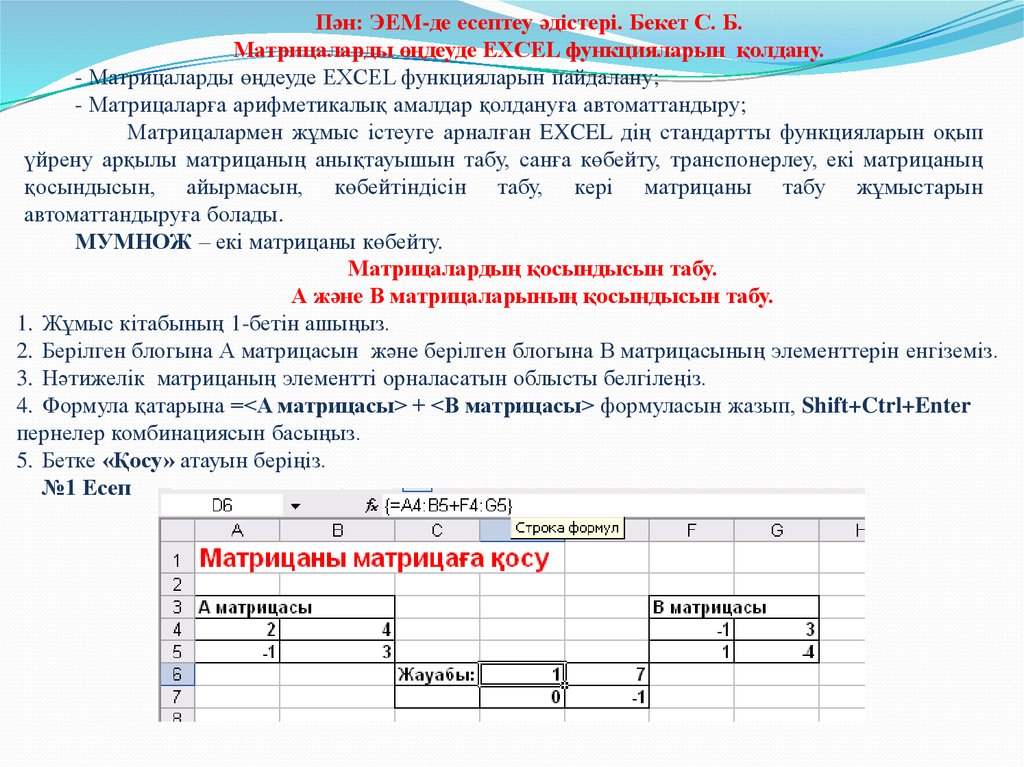
Пән: ЭЕМ-де есептеу әдістері. Бекет С. Б.
Матрицаларды өңдеуде EXCEL функцияларын қолдану.
- Матрицаларды өңдеуде ЕXCEL функцияларын пайдалану;
- Матрицаларға арифметикалық амалдар қолдануға автоматтандыру;
Матрицалармен жұмыс істеуге арналған EXCEL дің стандартты функцияларын оқып
үйрену арқылы матрицаның анықтауышын табу, санға көбейту, транспонерлеу, екі матрицаның
қосындысын, айырмасын, көбейтіндісін табу, кері матрицаны табу жұмыстарын
автоматтандыруға болады.
МУМНОЖ – екі матрицаны көбейту.
Матрицалардың қосындысын табу.
А және В матрицаларының қосындысын табу.
1. Жұмыс кітабының 1-бетін ашыңыз.
2. Берілген блогына А матрицасын және берілген блогына В матрицасының элементтерін енгіземіз.
3. Нәтижелік матрицаның элементті орналасатын облысты белгілеңіз.
4. Формула қатарына =<A матрицасы> + <B матрицасы> формуласын жазып, Shift+Ctrl+Enter
пернелер комбинациясын басыңыз.
5. Бетке «Қосу» атауын беріңіз.
№1 Есеп

10.

Пән: Алгебра. Жүсіпбекова М.У.
ә) Матрицаны санға көбейту
Кез-келген А матрицаны a санына көбейту депэлементтері мына формуламен анықталады:
Ñij aij ,
C A íåìåñå C A
және оның кез-келген
i 1, m, j 1, n
Сонымен, берілген А матрицаны a санына көбейту керек. Матрицаны санға көбейткенде мынадай қасиеттер
орындалады:
1.Сандар көбейткіштеріне терімділік қасиет:
A A
2.Матрицалардың қосындыларына терімділік қасиет:
( A B) A B
3. Сандардың қосындысына үлестірімділік қасиет:
( ) A A
Мысал №3
Берілген санға матрицаны көбейтіңіз
3,
2 1 4
A 0 5 3
2 1 0
2 1 4 6 3 12
A 3 0 5 3 0 15 9
2 1 0 6 3 0
6 3
3A 0 15
6 3
12
9
0

11.

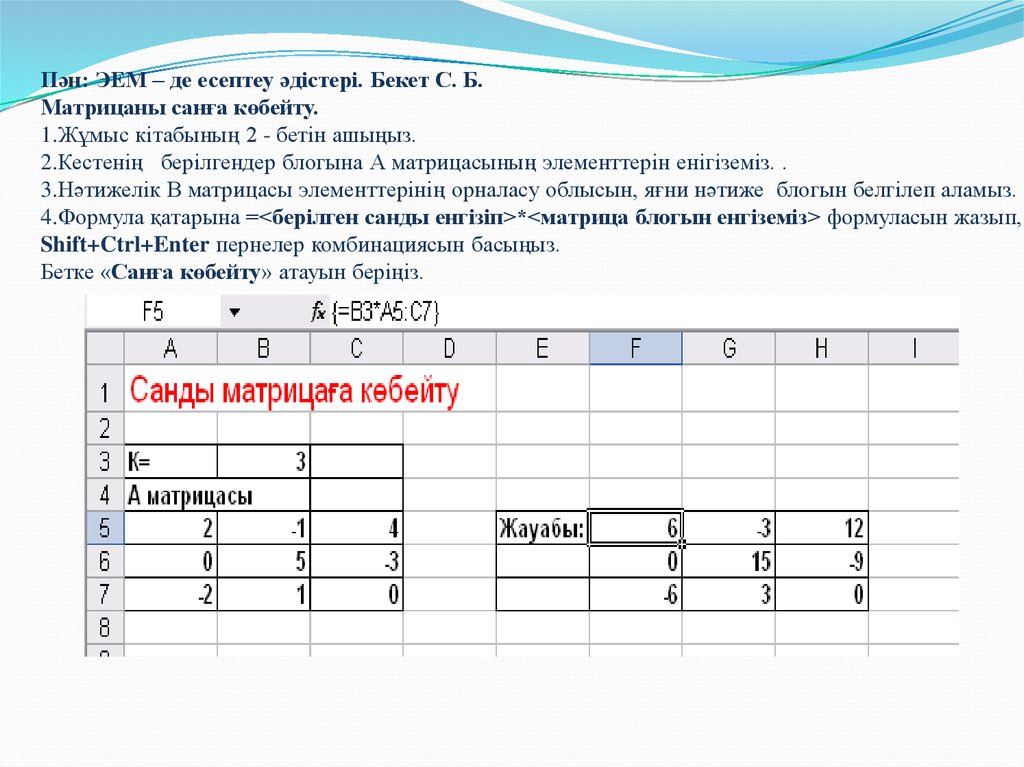
Пән: ЭЕМ – де есептеу әдістері. Бекет С. Б.
Матрицаны санға көбейту.
1.Жұмыс кітабының 2 - бетін ашыңыз.
2.Кестенің берілгендер блогына А матрицасының элементтерін енігіземіз. .
3.Нәтижелік В матрицасы элементтерінің орналасу облысын, яғни нәтиже блогын белгілеп аламыз.
4.Формула қатарына =<берілген санды енгізіп>*<матрица блогын енгіземіз> формуласын жазып,
Shift+Ctrl+Enter пернелер комбинациясын басыңыз.
Бетке «Санға көбейту» атауын беріңіз.

12. Пән: Алгебра. Жүсіпбекова М.У.   б) Матрицаны матрицаға көбейту Берілген ретті А матрицасының ретті В матрицасына көбейтіндісі

Пән: Алгебра. Жүсіпбекова М.У.
б) Матрицаны матрицаға көбейту
Берілген m n ретті А матрицасының
m k ретті С матрицаны айтамыз.
Ал оның кез-келген элементтері
n
n k
ретті В матрицасына көбейтіндісі деп-
C A B
Cij мына формуладан анықталады:
C ij aik bkj .
i 1, m, j 1, n
i 1
Мысал №4
Берілген А және В матрицаларының көбейтіндісін табыңыз.
3 1 1
1 1 1
A 2 1 2 , B 2 1 1
1 2 3
1 0 1
C A B
3 1 1 2 1 1 3 1 1 ( 1) 1 0 3 ( 1) 1 1 1 1 6 2 1
3 1 1 1 1 1
2
1
1
2 1 1 2 2 1 2 1 1 ( 1) 2 0 2 1 1 1 2 1 6 1 1
2 1 2
1 2 3
1 1 2 2 3 1 1 1 2 ( 1) 3 0 1 1 2 1 3 1 8 1 4
1 0 1
6 2 1
Ñ 6 1 1
8 1 4

13.

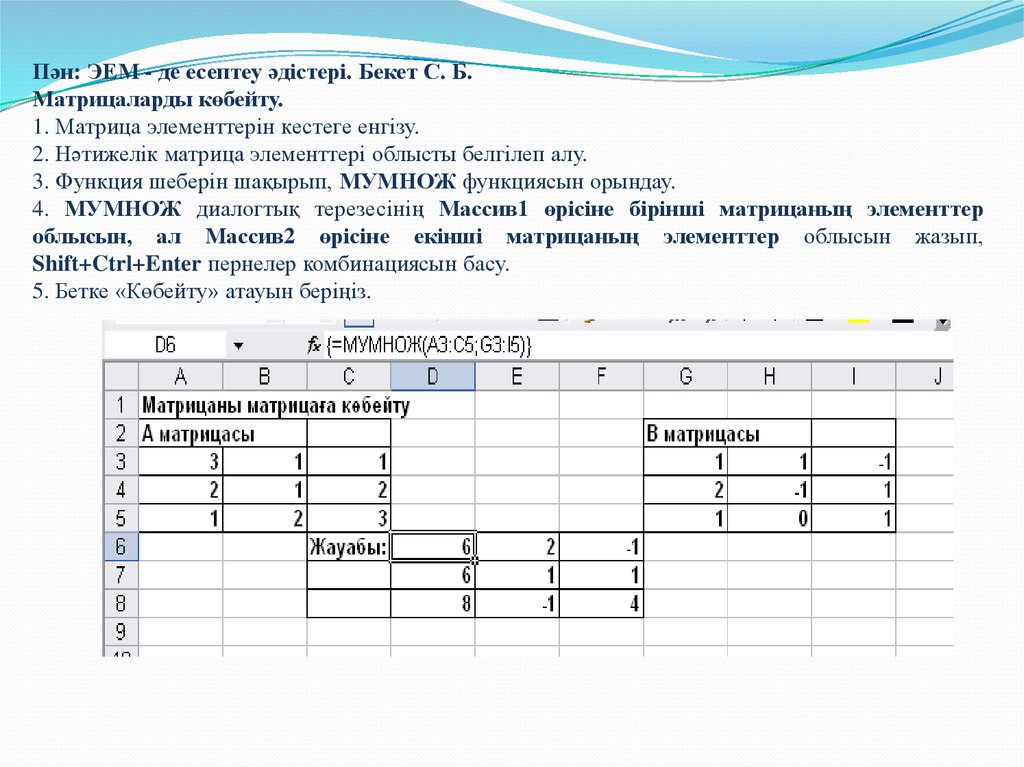
Пән: ЭЕМ - де есептеу әдістері. Бекет С. Б.
Матрицаларды көбейту.
1. Матрица элементтерін кестеге енгізу.
2. Нәтижелік матрица элементтері облысты белгілеп алу.
3. Функция шеберін шақырып, МУМНОЖ функциясын орындау.
4. МУМНОЖ диалогтық терезесінің Массив1 өрісіне бірінші матрицаның элементтер
облысын, ал Массив2 өрісіне екінші матрицаның элементтер облысын жазып,
Shift+Ctrl+Enter пернелер комбинациясын басу.
5. Бетке «Көбейту» атауын беріңіз.

14.

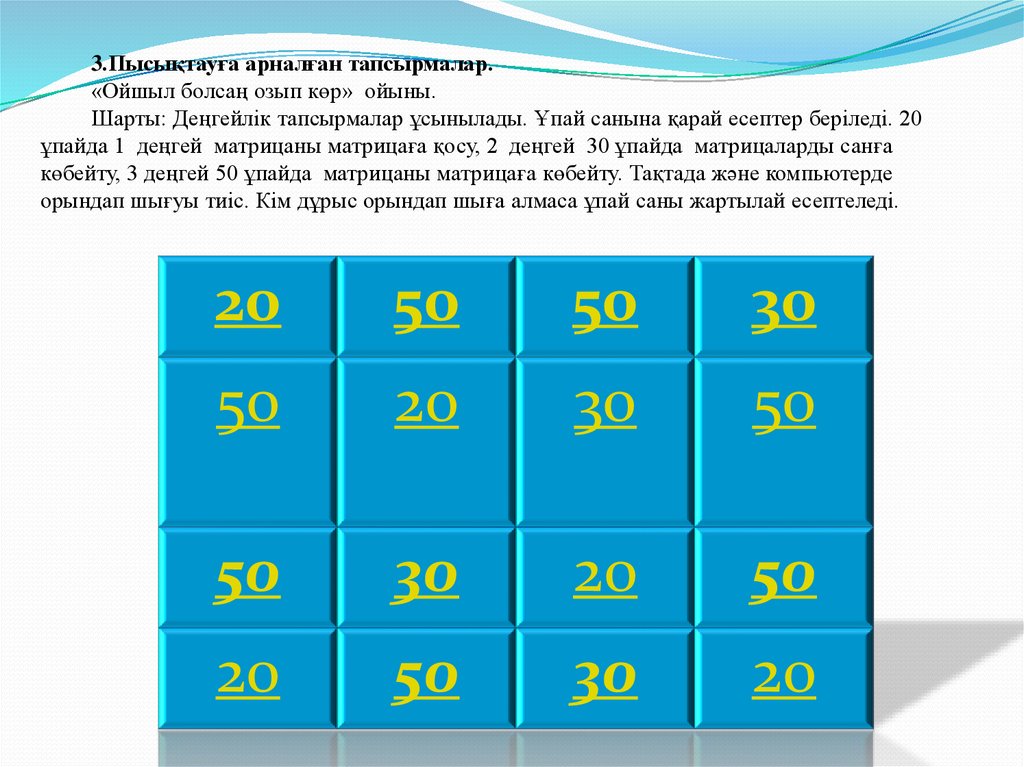
3.Пысықтауға арналған тапсырмалар.
«Ойшыл болсаң озып көр» ойыны.
Шарты: Деңгейлік тапсырмалар ұсынылады. Ұпай санына қарай есептер беріледі. 20
ұпайда 1 деңгей матрицаны матрицаға қосу, 2 деңгей 30 ұпайда матрицаларды санға
көбейту, 3 деңгей 50 ұпайда матрицаны матрицаға көбейту. Тақтада және компьютерде
орындап шығуы тиіс. Кім дұрыс орындап шыға алмаса ұпай саны жартылай есептеледі.
20
50
50
30
50
20
30
50
50
30
20
50
20
50
30
20

15.

C AB BA
Ñ A 2B
2

16.

2 1
7 4
A , B
0
3
5
3
2 1
7 4
, B
A
0 3
5 3
Жауабы

17.

1 2 1
4 1 1
A 2 1 2 , B 4 2 0
1 2 3
1 2 1
2 1
7 4
, B
A
0 3
5 3
Жауабы

18.

Ñ A 2B
2
10 3
C
10
3
2 1
7 4
, B
A
0 3
5 3

19.

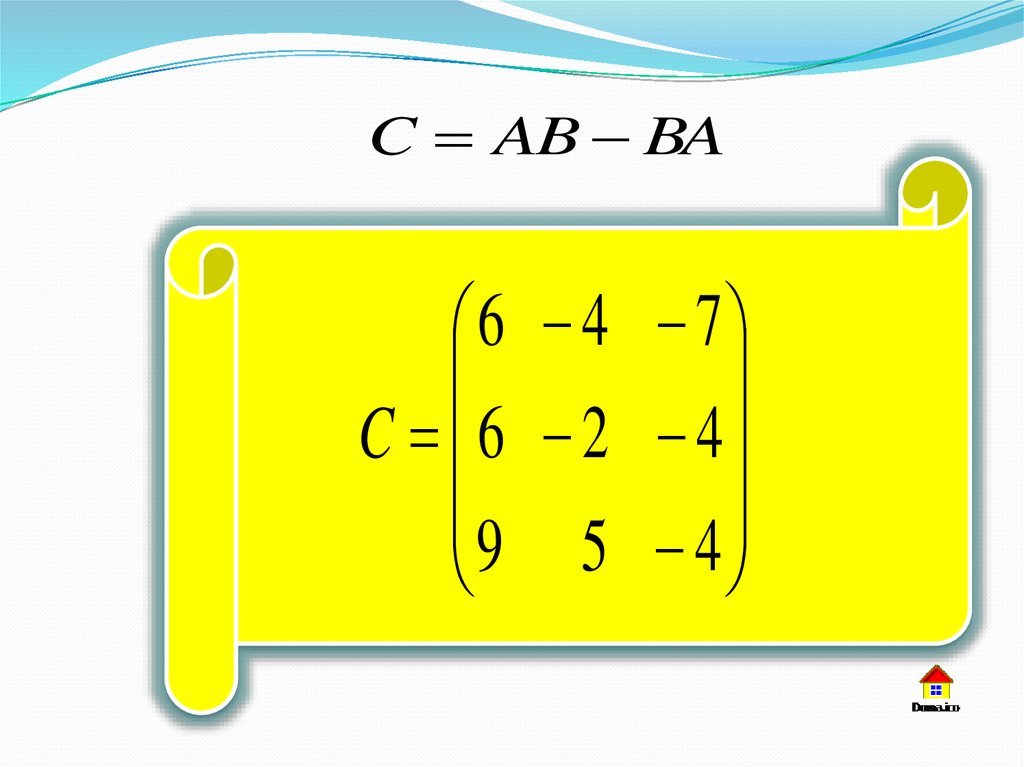
C AB BA
6 4 7
C 6 2 4
9 5 4
2 1
7 4
, B
A
0 3
5 3

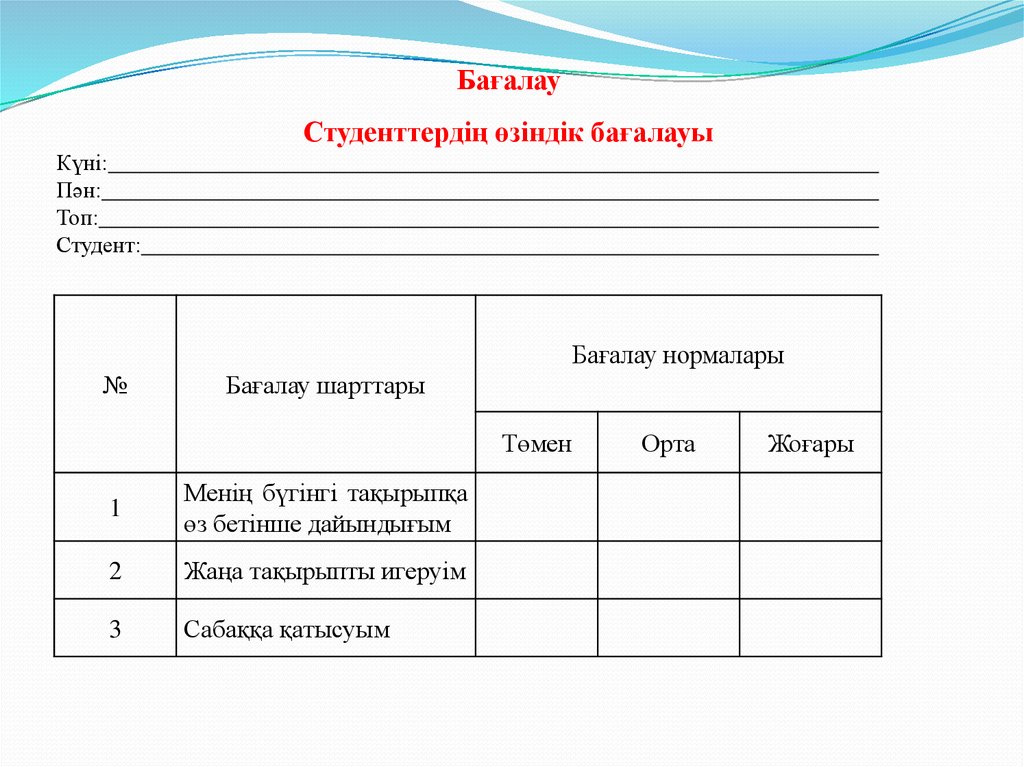
20. Бағалау

Студенттердің өзіндік бағалауы
Күні:
Пән:
Топ:
Студент:
Бағалау нормалары
№
Бағалау шарттары
Төмен
1
Менің бүгінгі тақырыпқа
өз бетінше дайындығым
2
Жаңа тақырыпты игеруім
3
Сабаққа қатысуым
Орта
Жоғары

21.

Топтың өзара бағалауы
Күні:
Пән:
Топ:
Топ басшысы
№
Бағалау нормалары
Бағалау шарттары
Төмен
1
2
3
Топ ұжымының татулығы
Сабақ барысындағы топ
белсенділігі
Сөйлеу мәдениеттілігі мен
шеберлігі
Орта
Жоғары

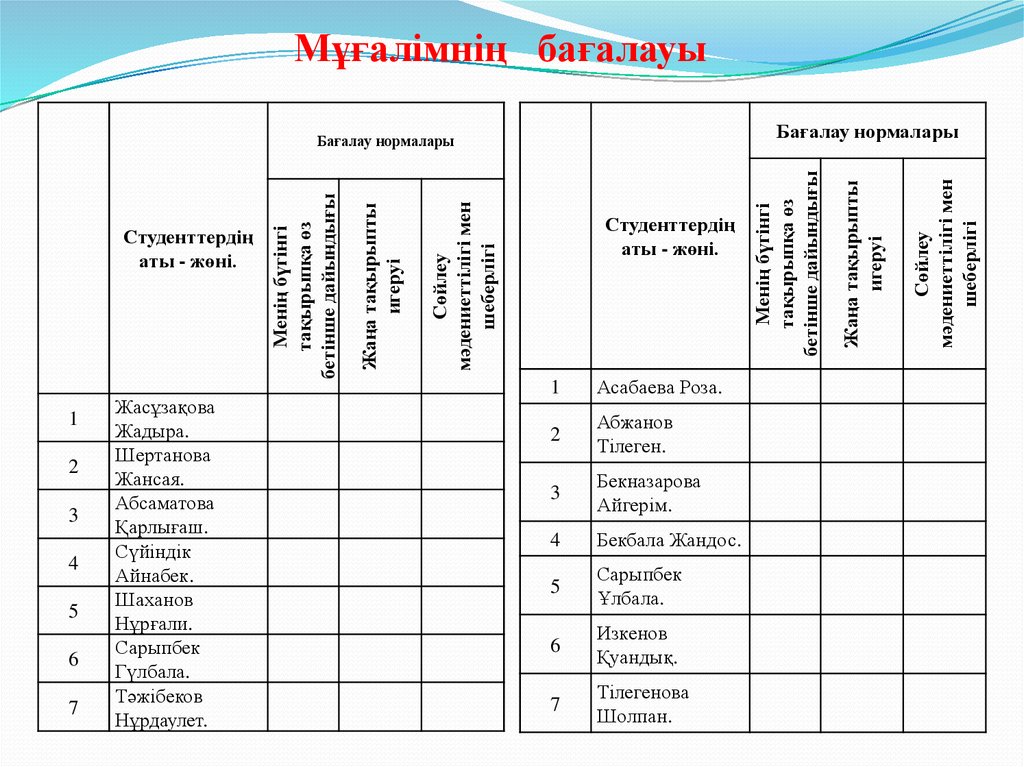
22. Мұғалімнің бағалауы

1
2
3
4
5
6
7
Жасұзақова
Жадыра.
Шертанова
Жансая.
Абсаматова
Қарлығаш.
Сүйіндік
Айнабек.
Шаханов
Нұрғали.
Сарыпбек
Гүлбала.
Тәжібеков
Нұрдаулет.
1
Асабаева Роза.
2
Абжанов
Тілеген.
3
Бекназарова
Айгерім.
4
Бекбала Жандос.
5
Сарыпбек
Ұлбала.
6
Изкенов
Қуандық.
7
Тілегенова
Шолпан.
Сөйлеу
мәдениеттілігі мен
шеберлігі
Студенттердің
аты - жөні.
Жаңа тақырыпты
игеруі
Сөйлеу
мәдениеттілігі мен
шеберлігі
Жаңа тақырыпты
игеруі
Менің бүгінгі
тақырыпқа өз
бетінше дайындығы
Студенттердің
аты - жөні.
Менің бүгінгі
тақырыпқа өз
бетінше дайындығы
Бағалау нормалары
Бағалау нормалары

23. Фотолар

24. Назар аударғандарыңызға рахмет!!!

Ғ. Мұратбаев атындағы Жетісай гуманитарлық-техникалық
колледжі
“Математика , информатика, физика және техникалық оқыту
құралдары “ кафедрасы
Орындағандар:
Бекет С. Б.
Жүсіпбекова М.