Похожие презентации:
Основы кинематики
1. Физика
• Лектор: Давлетшина МиляушаРафаэлевна, доцент кафедры
физики УГНТУ
2. Лекция 1 Введение. Основы кинематики Литература: Савельев В.А.Курс физики, 2008 г., том 1 Трофимова Т.И. Курс физики,2005 г.,
гл.13.
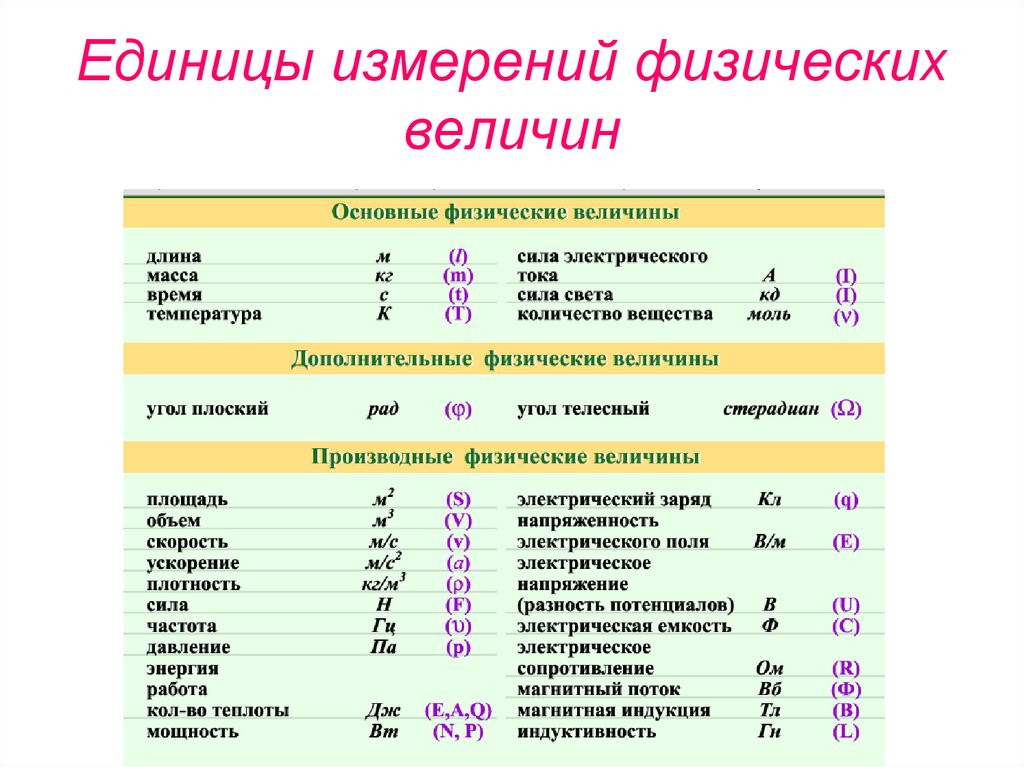
4. Единицы измерений физических величин
5. Приставки кратных и дольных единиц
6. Плакаты 9-10: Векторы
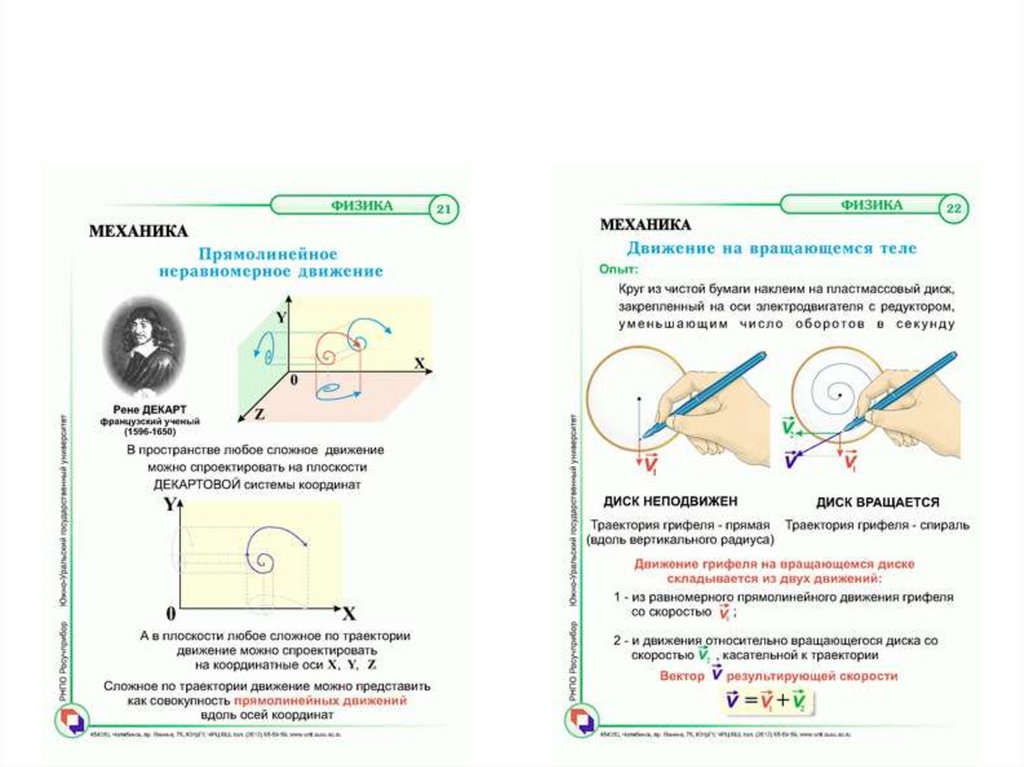
7. ДЕКАРТОВЫ КООРДИНАТЫ
Декартова система координат [поимени
франц.
философа
и
математика Р. Декарта (1596 - 1650)],
- система координат на плоскости или
в пространстве, обычно с взаимно
перпендикулярными
осями
и
одинаковыми масштабами по осям прямоугольные Д. к.
8.
• Дека́рт Рене заложил основыаналитической геометрии, дал понятия
переменной величины и функции, ввёл
многие алгебраические обозначения.
Высказал закон сохранения количества
движения, дал понятие импульса
силы. Общая причина движения, по
Декарту, — Бог, который сотворил
материю, движение и покой.
9. Портрет René Descartes (1596-1650) Музей Лувр, Richelieu, 2nd floor, room 27
10. Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат X , Y и Z. Оси
Прямоугольнаяпространстве
система
образуется
координат
тремя
в
взаимно
перпендикулярными осями координат X , Y и Z. Оси
координат
пересекаются
называется
выбрано
началом
в
точке
координат,
положительное
на
O,
которая
каждой
направление,
оси
указанное
стрелками, и единица измерения отрезков на осях.
X — ось абсцисс, Y — ось ординат, Z — ось аппликат.
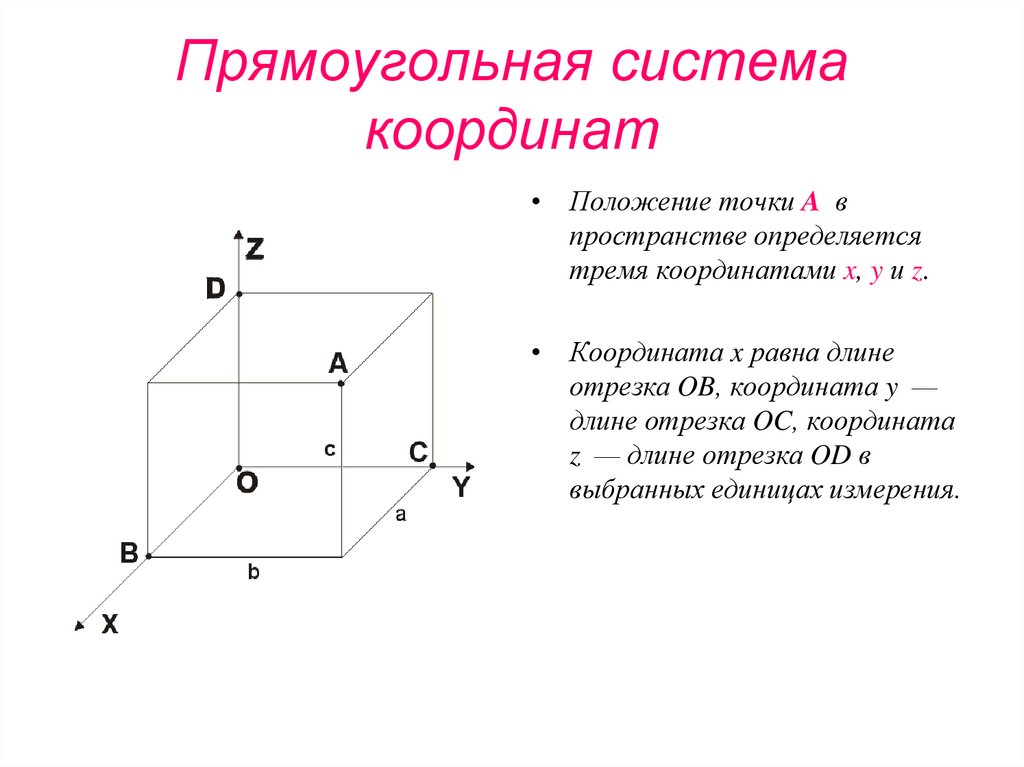
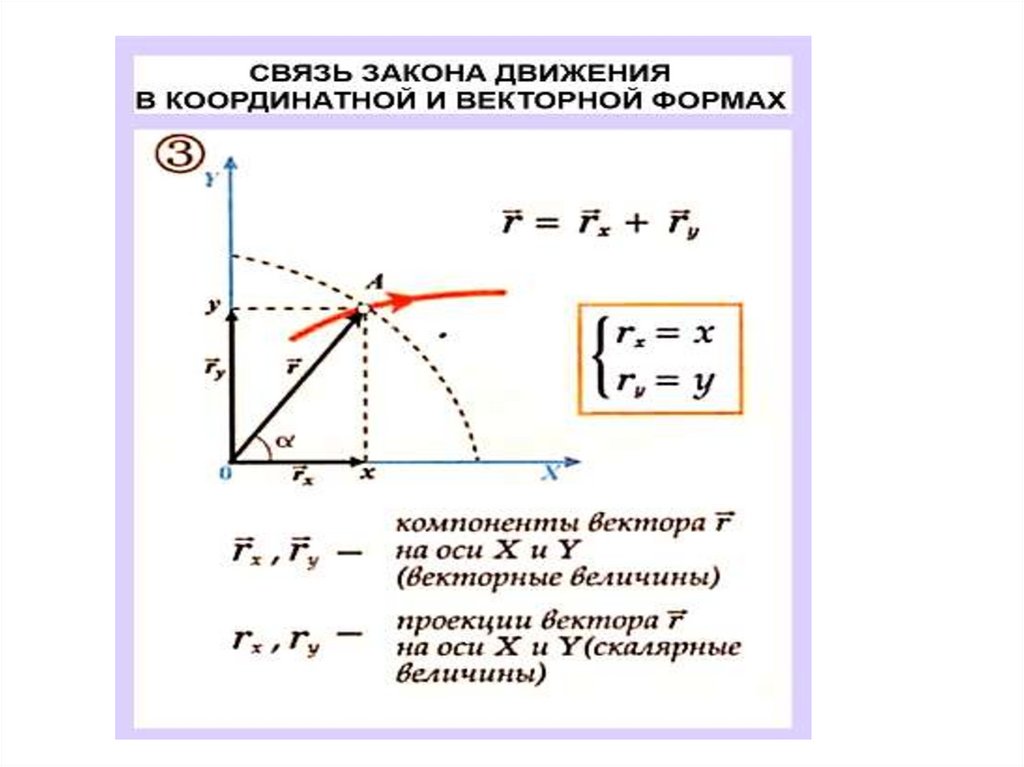
11. Прямоугольная система координат
• Положение точки A впространстве определяется
тремя координатами x, y и z.
• Координата x равна длине
отрезка OB, координата y —
длине отрезка OC, координата
z — длине отрезка OD в
выбранных единицах измерения.
12.
• Прямоугольная система координат такжеописывается
сонаправленных
Количество
системы
набором
ортов,
осями
координат.
с
ортов
равно
координат
и
размерности
все
они
перпендикулярны друг другу. Такие орты
составляют
притом ортонормированный.
базис,
13.
• В трёхмерном случае такие ортыобычно обозначаются
–i , j и k или ex , ey и ez .
Могут также применяться обозначения со
стрелками i , j и k или другие в
соответствии с обычным способом
обозначения векторов в той или иной
литературе.
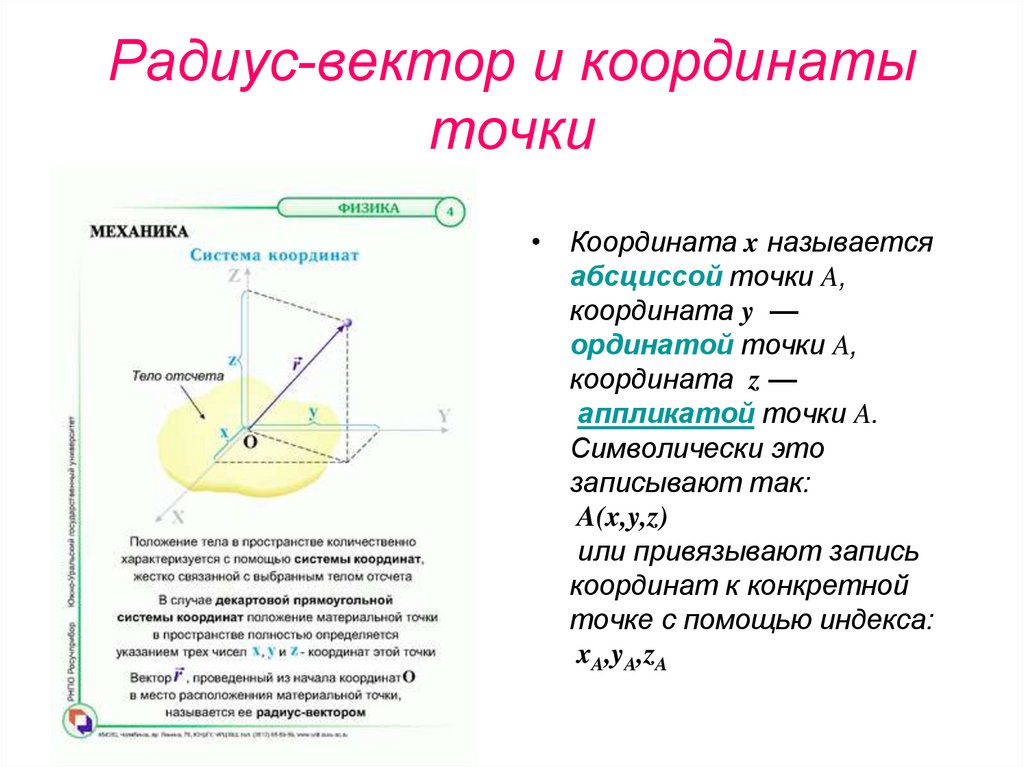
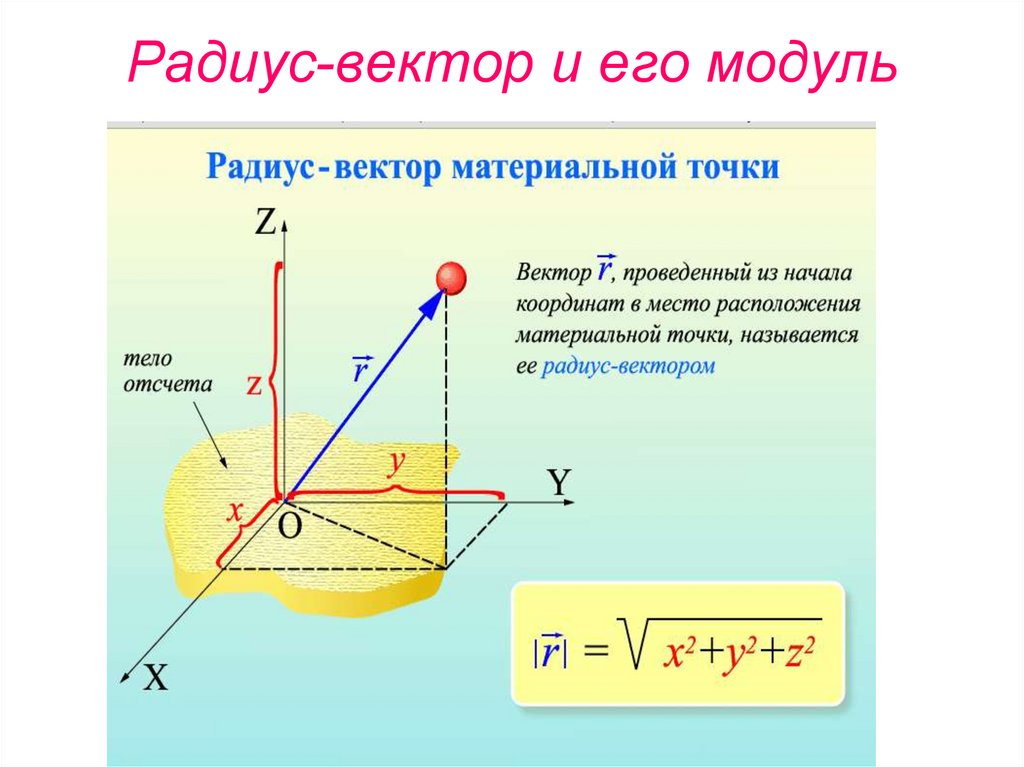
14. Радиус-вектор и координаты точки
• Координата x называетсяабсциссой точки A,
координата y —
ординатой точки A,
координата z —
аппликатой точки A.
Символически это
записывают так:
A(x,y,z)
или привязывают запись
координат к конкретной
точке с помощью индекса:
xA,yA,zA
15. Радиус-вектор и его модуль
16.
17.
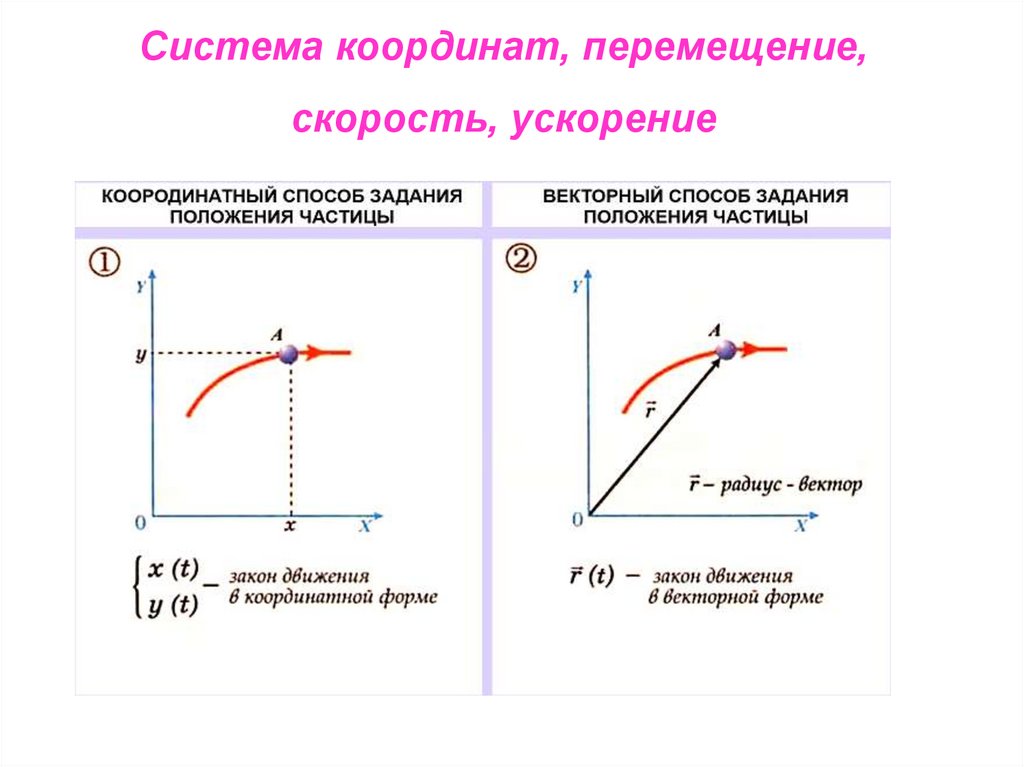
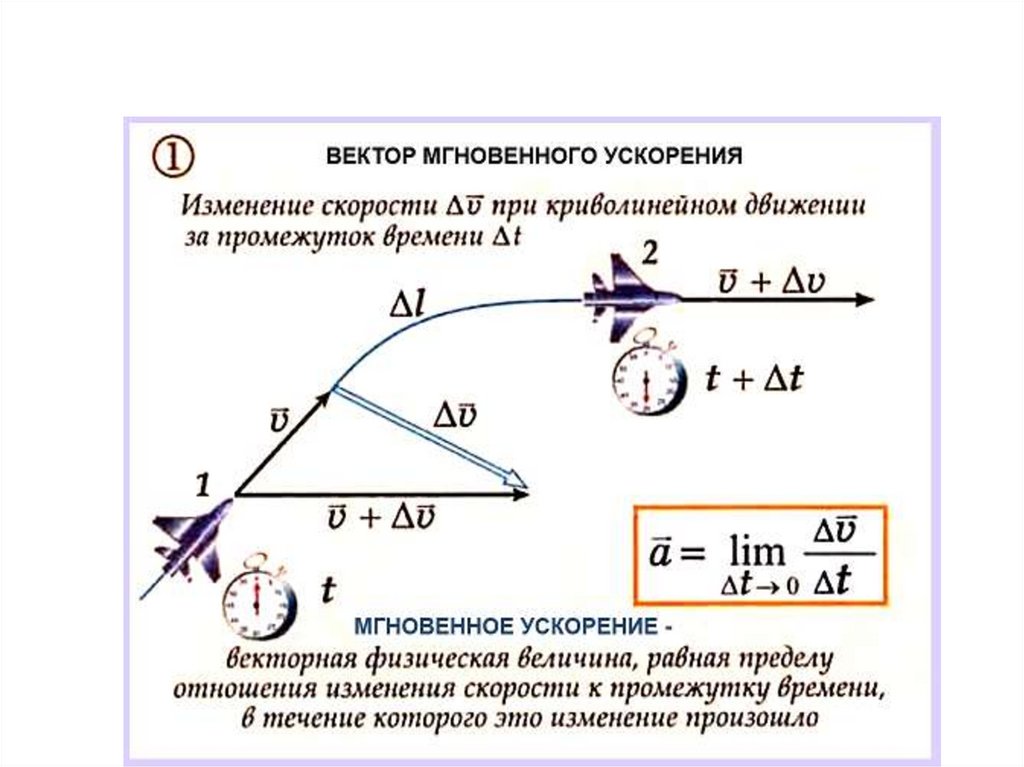
18. Система координат, перемещение, скорость, ускорение
19.
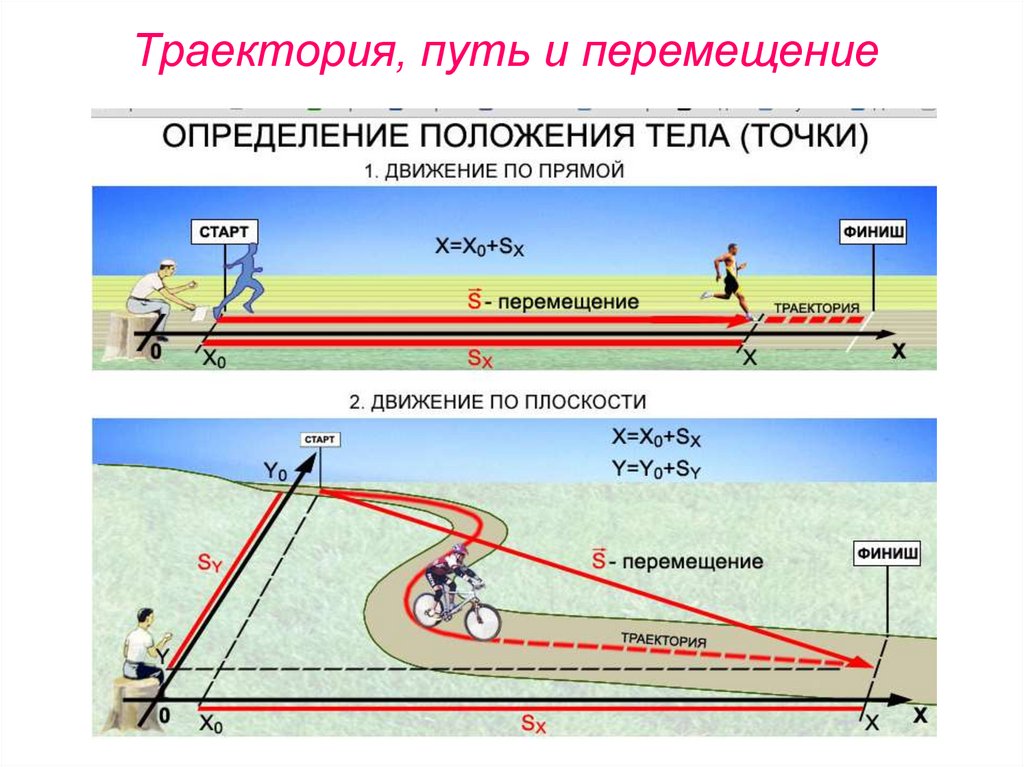
20. Траектория, путь и перемещение
21.
22.
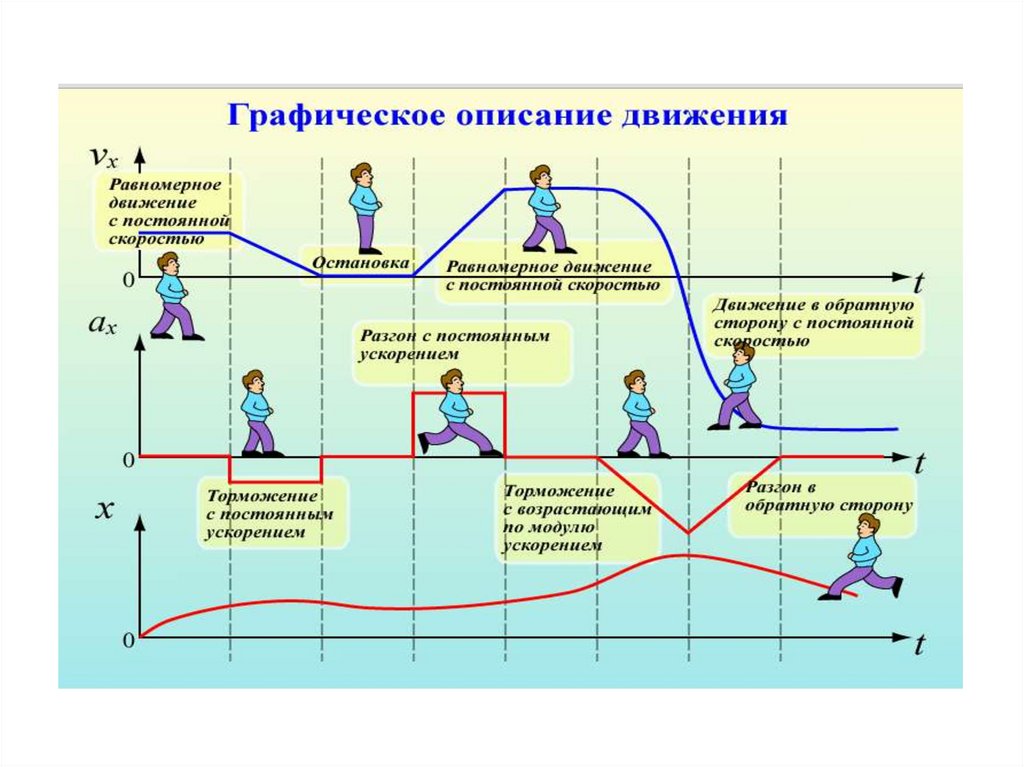
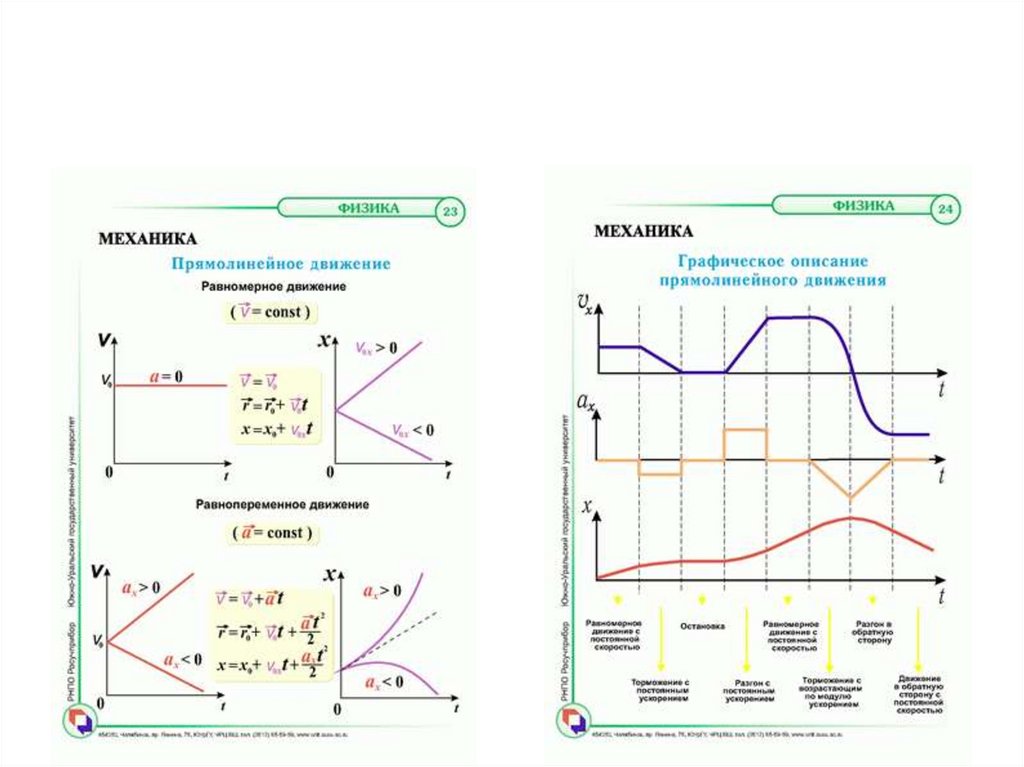
23.
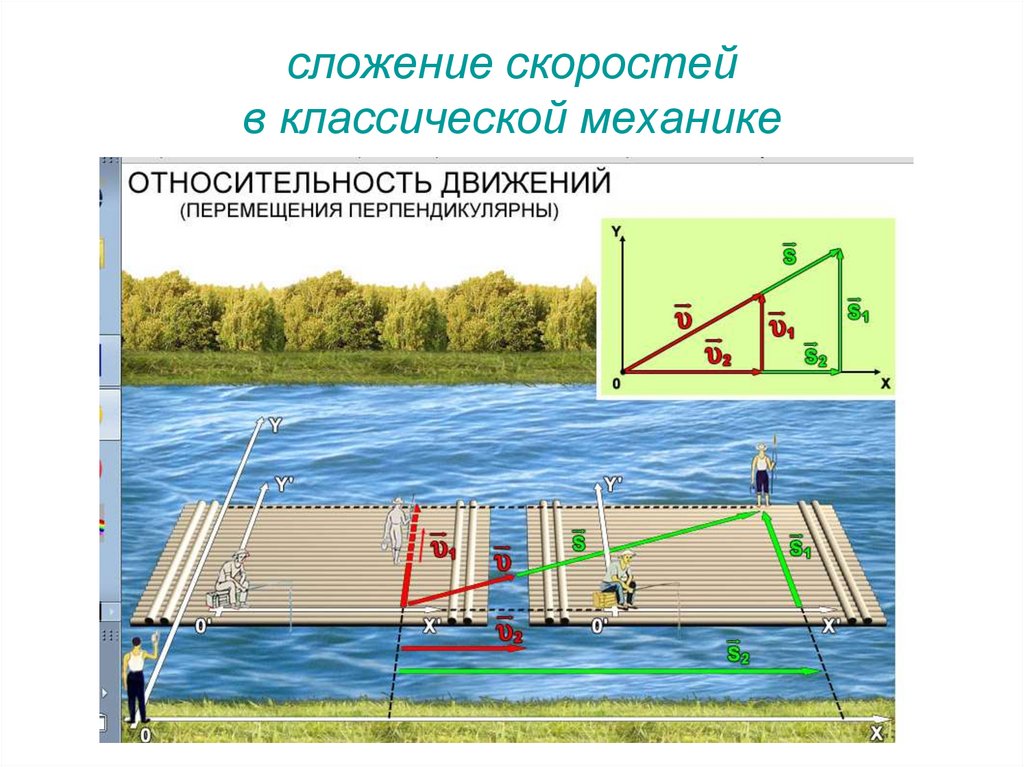
24. сложение скоростей в классической механике
25.
26.
27.
28.
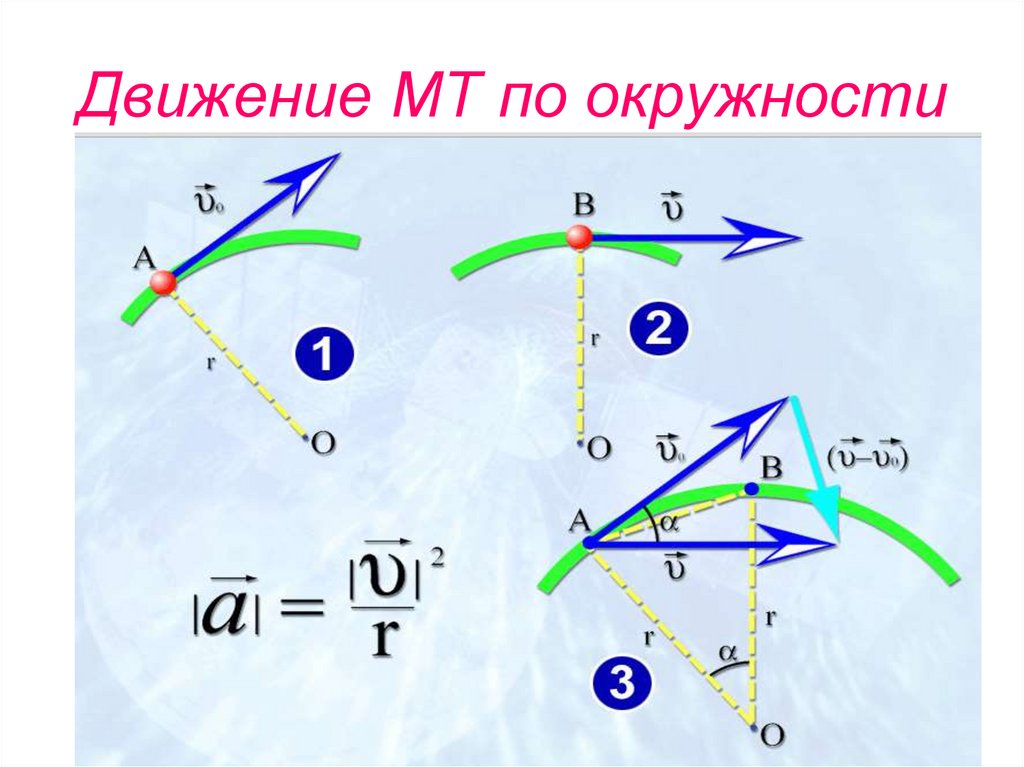
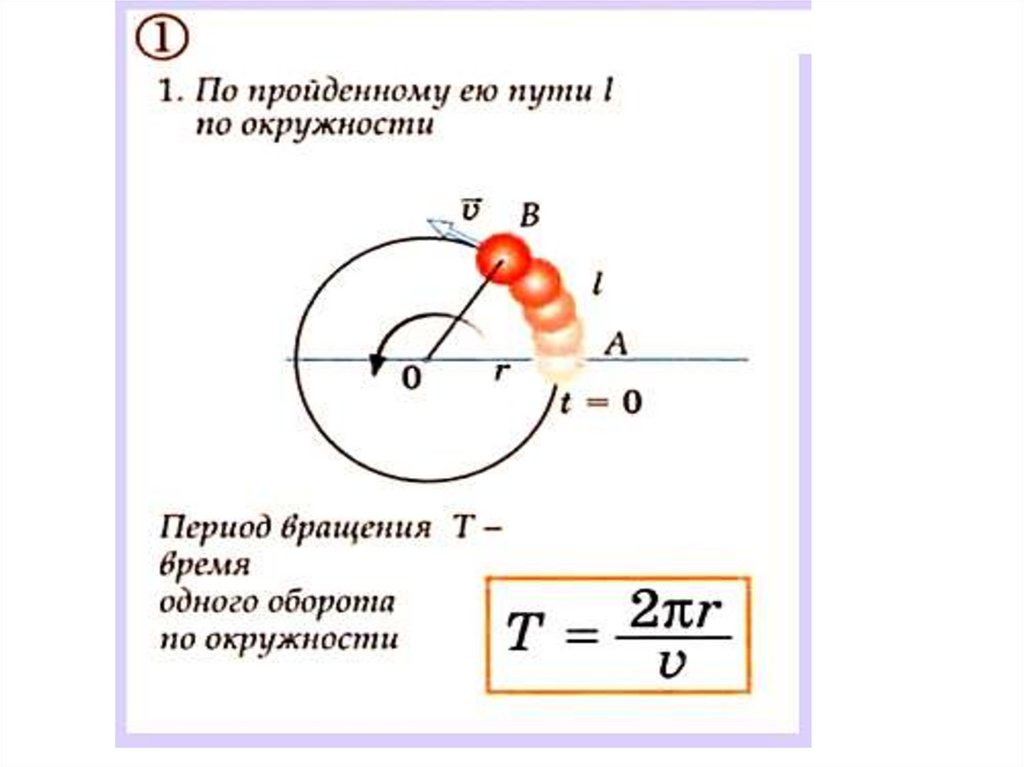
29. Движение МТ по окружности
30.
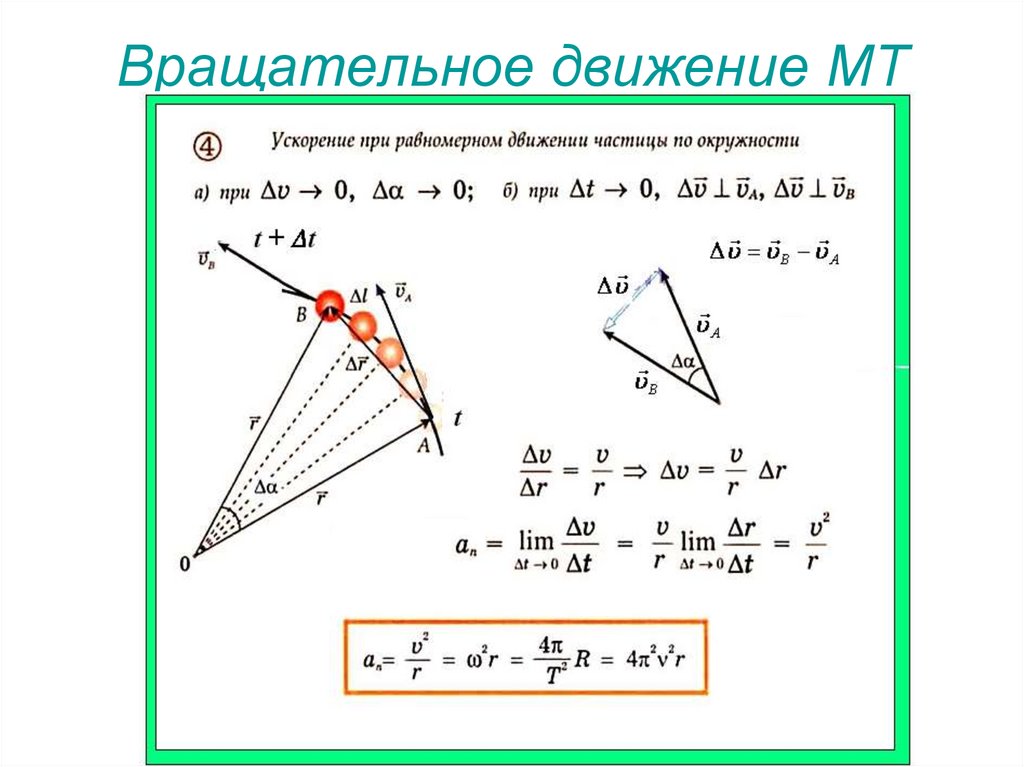
31. Вращательное движение МТ
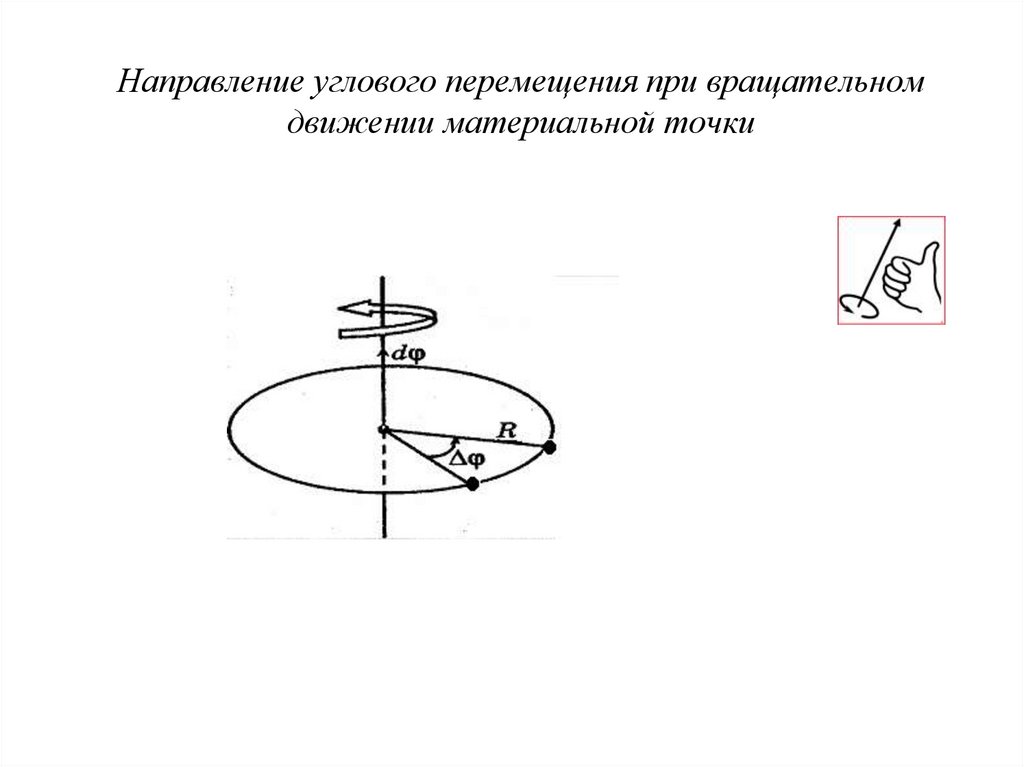
32. Направление углового перемещения при вращательном движении материальной точки
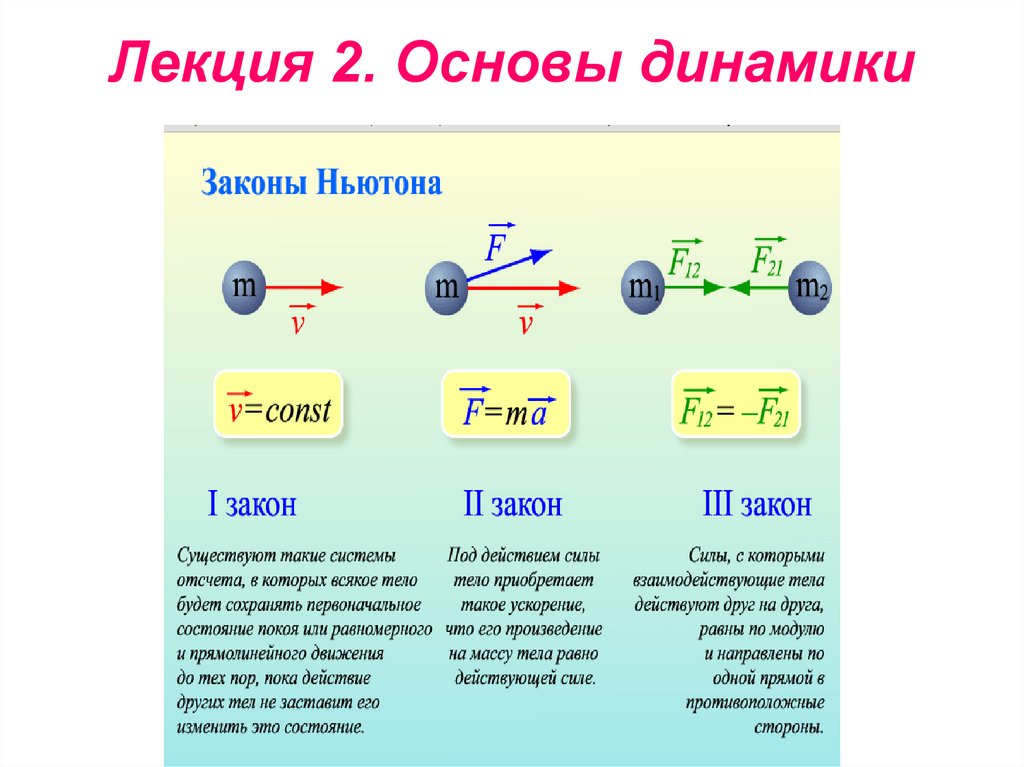
33. Лекция 2. Основы динамики
34.
35. НЬЮТОН Исаак. (4.I 1643 — 31.III 1727). Английский физик, астроном и математик, член Лондонского королевского общества (1672),
НЬЮТОН Исаак. (4.I 1643 — 31.III 1727). Английский физик,астроном и математик, член Лондонского королевского
общества (1672), его президент (с 1703). Один из
основоположников современного естествознания.
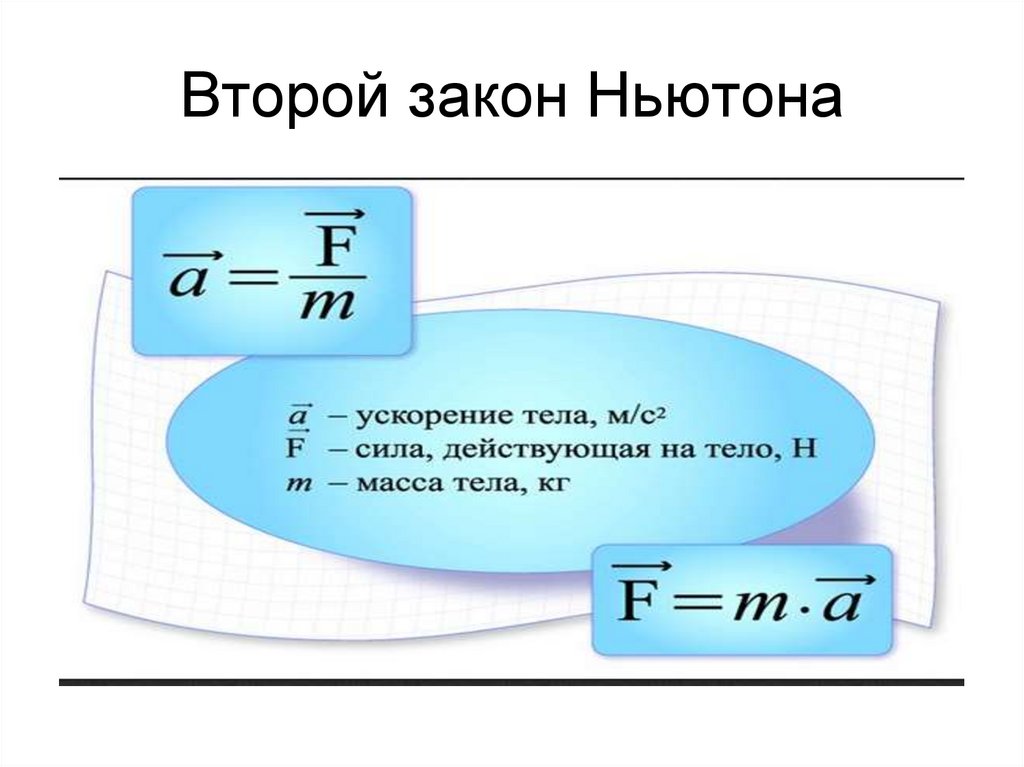
36. Второй закон Ньютона
37.
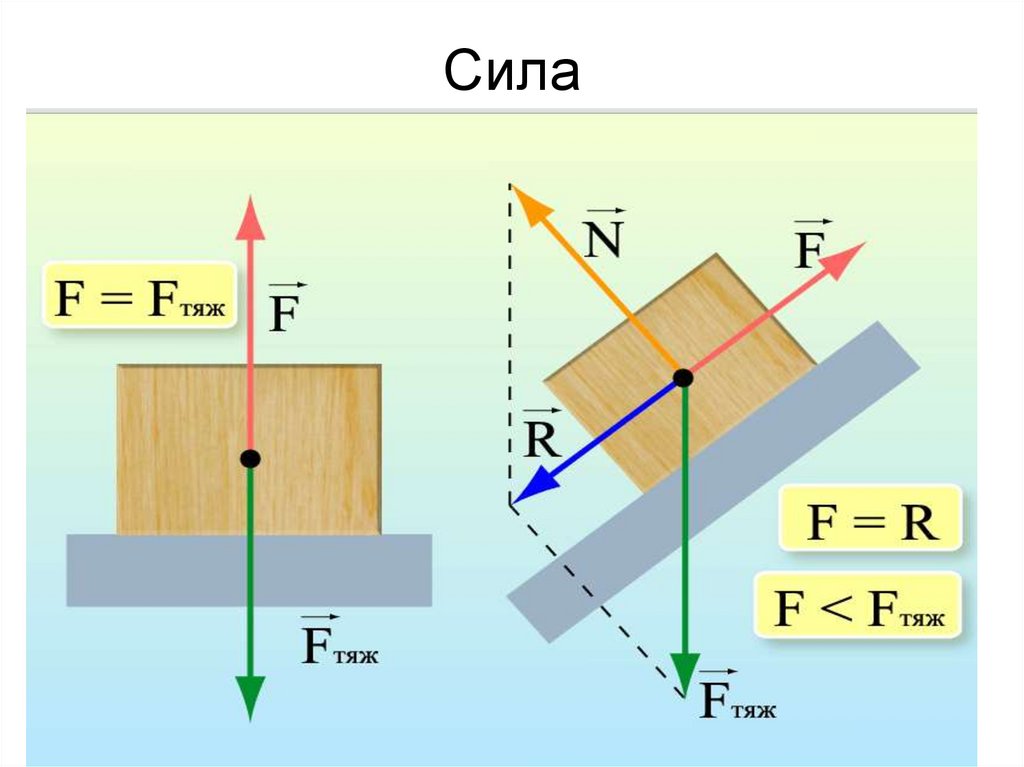
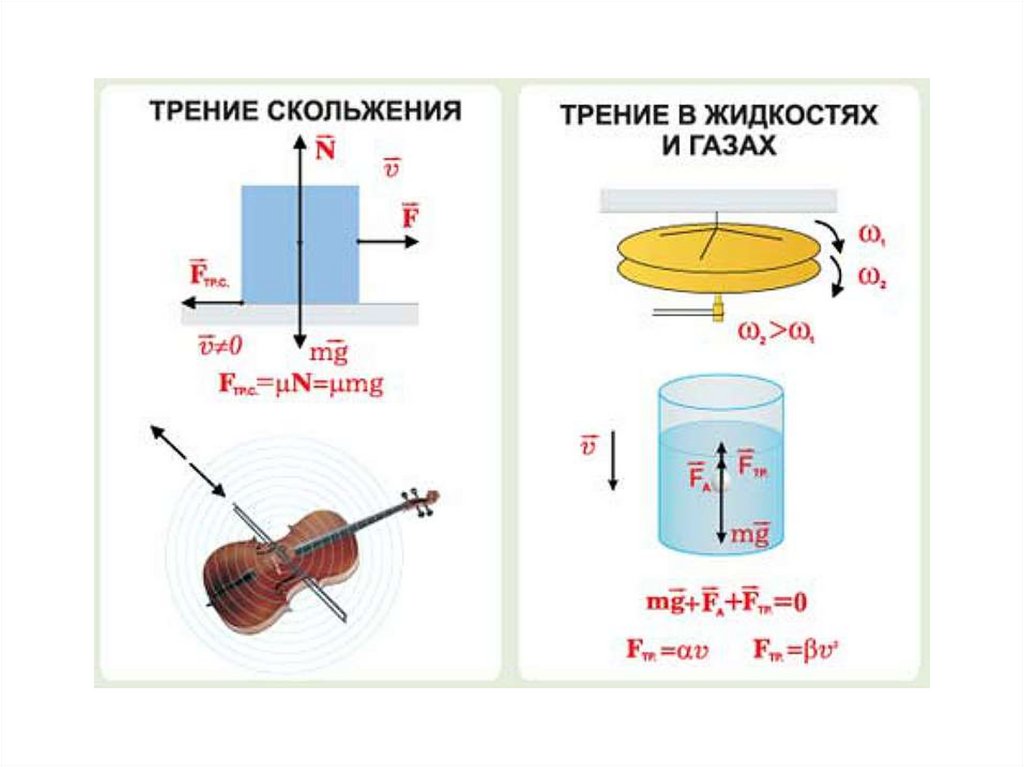
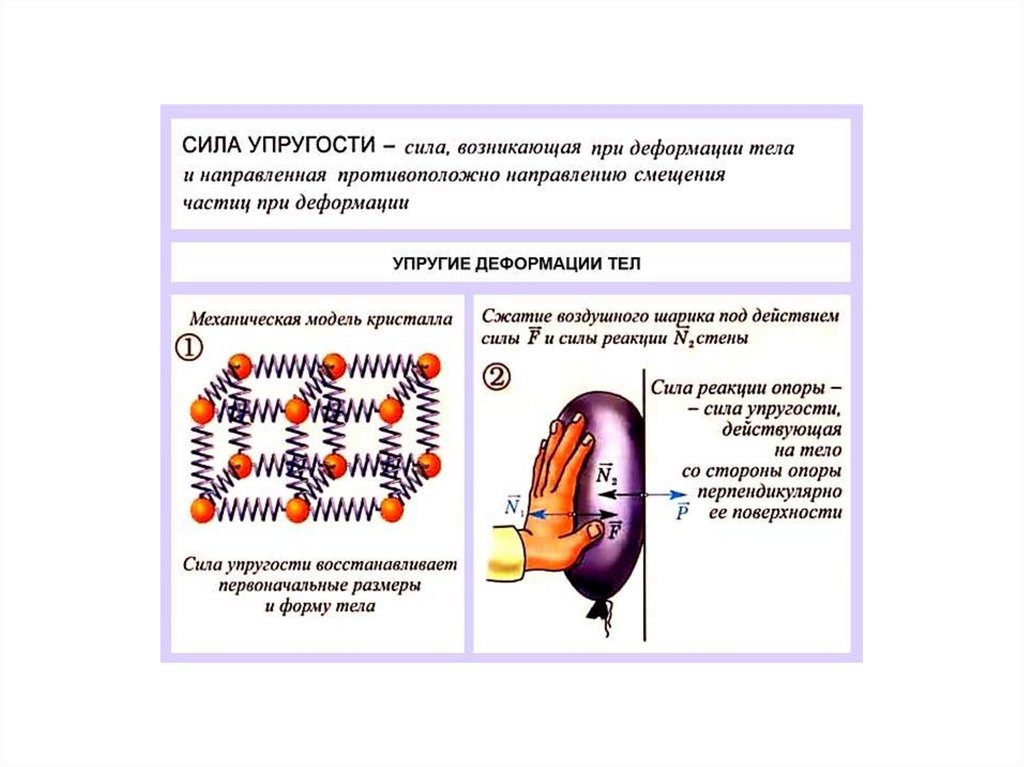
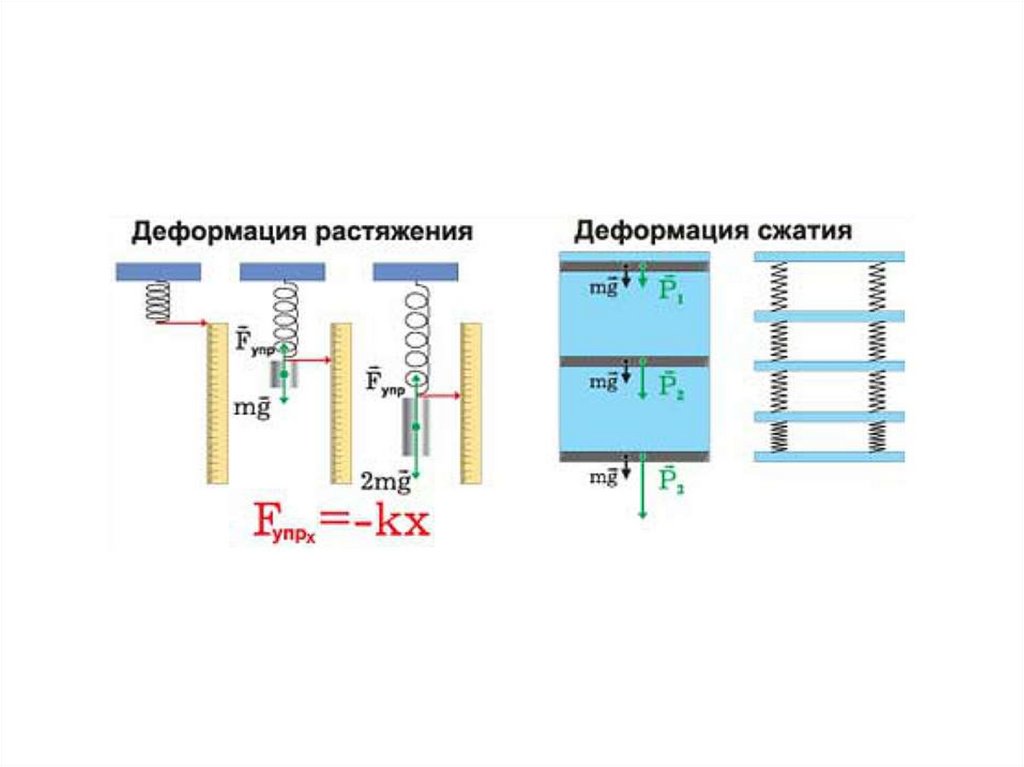
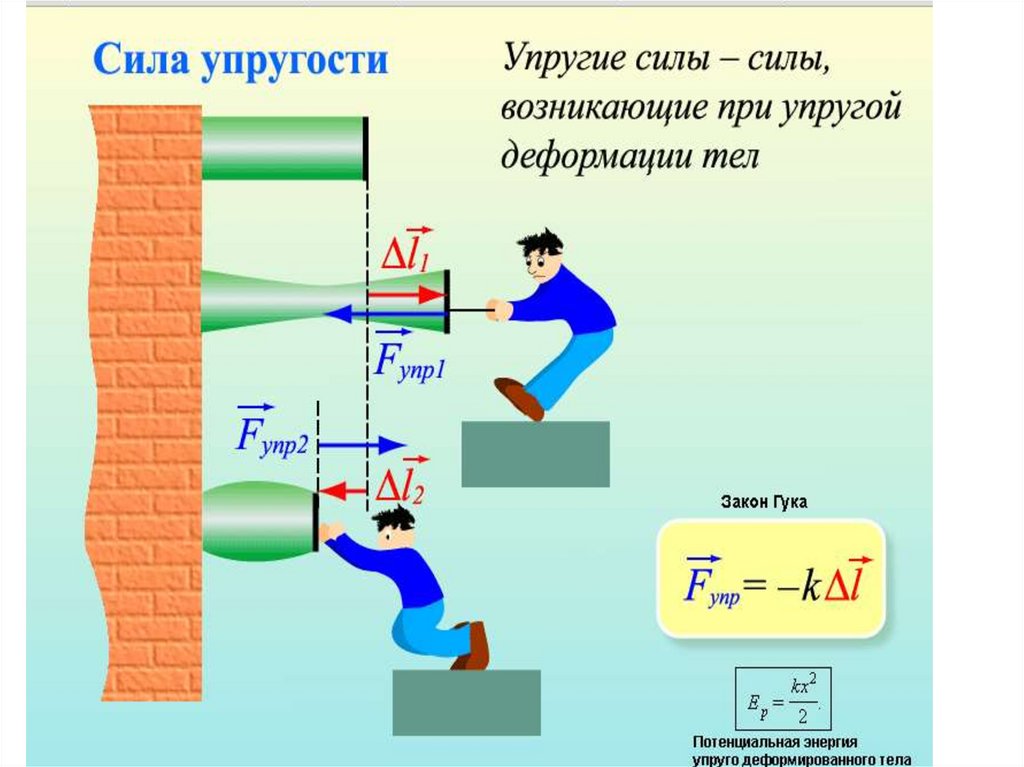
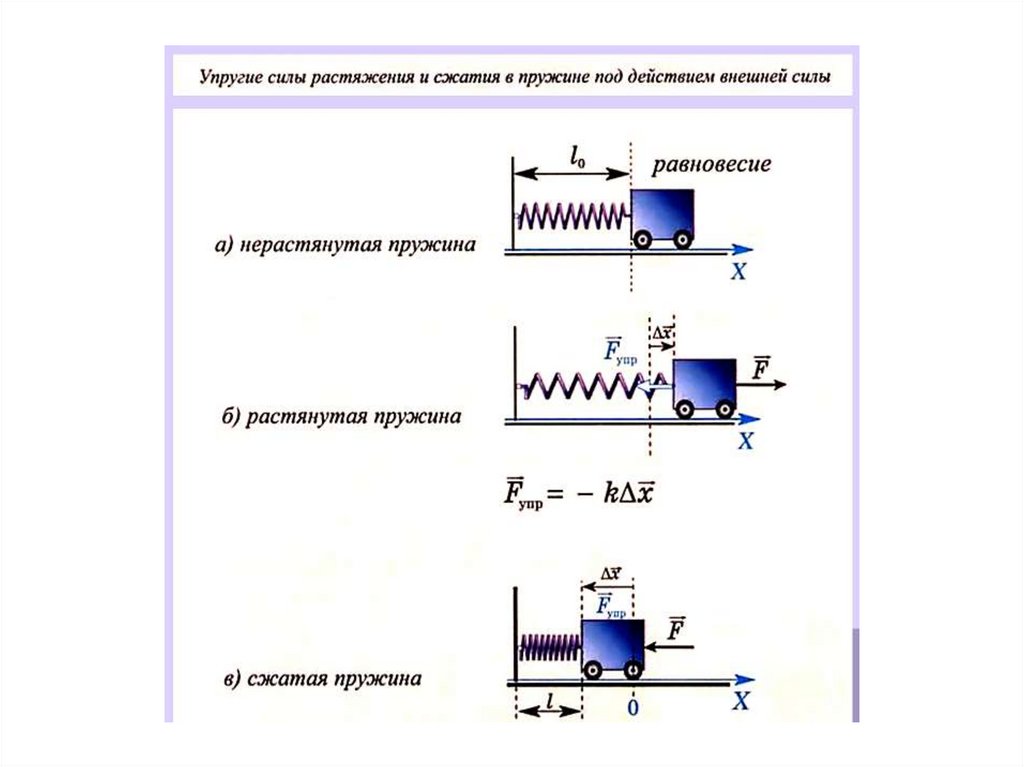
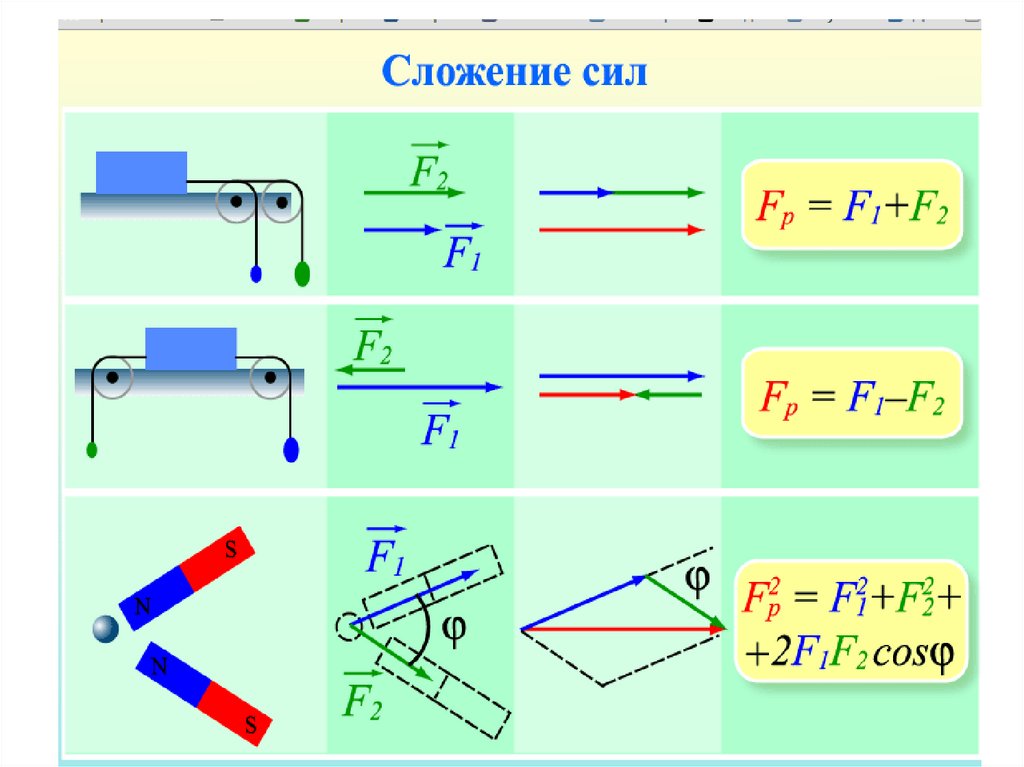
38. Сила
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
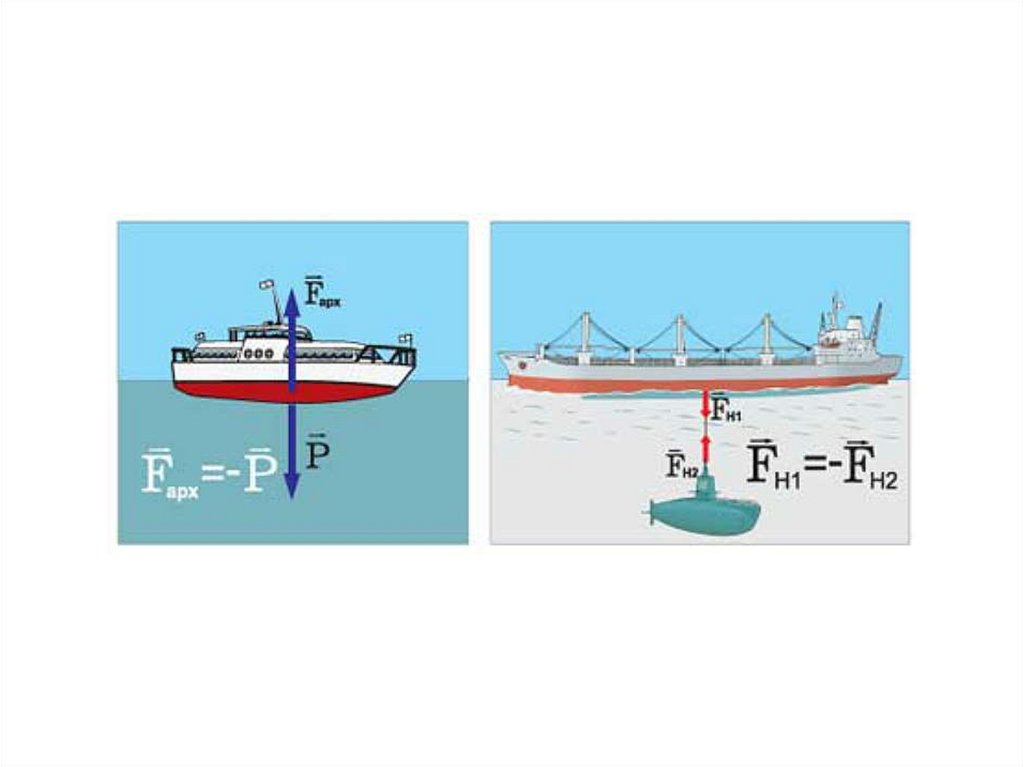
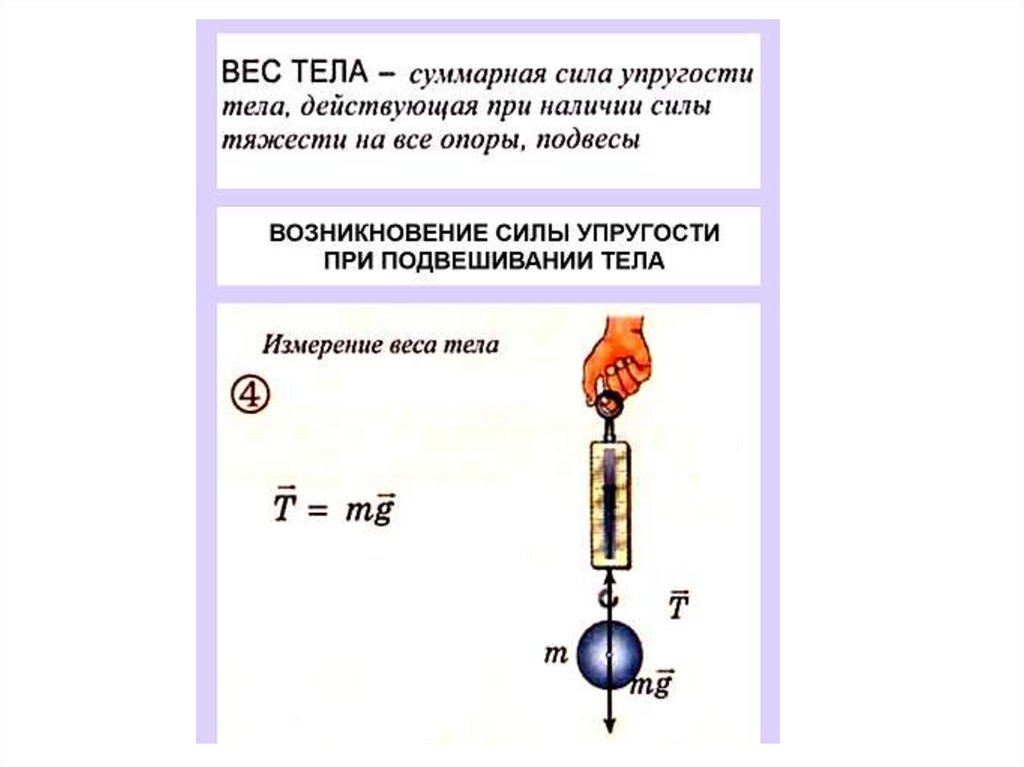
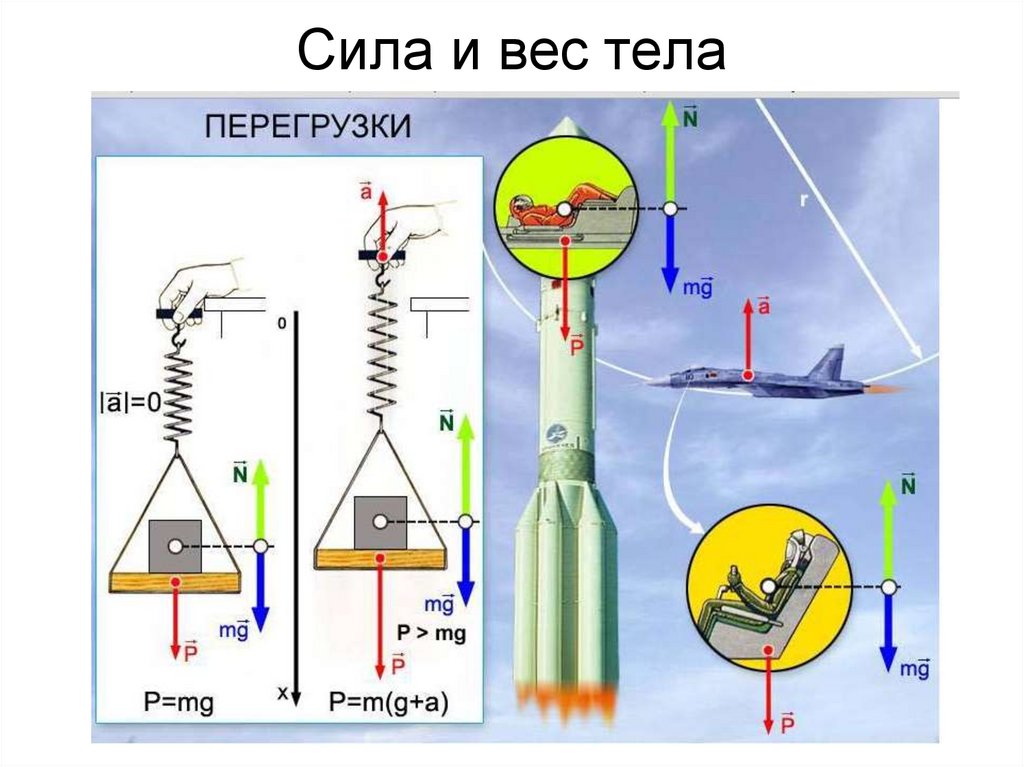
49. Сила и вес тела
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
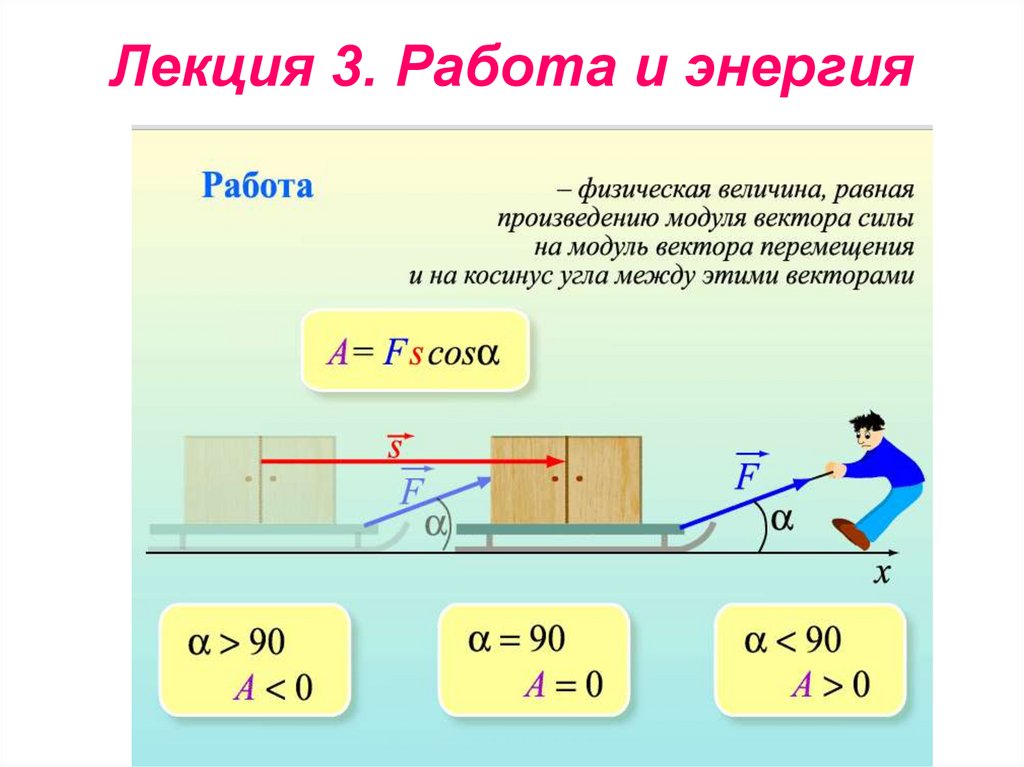
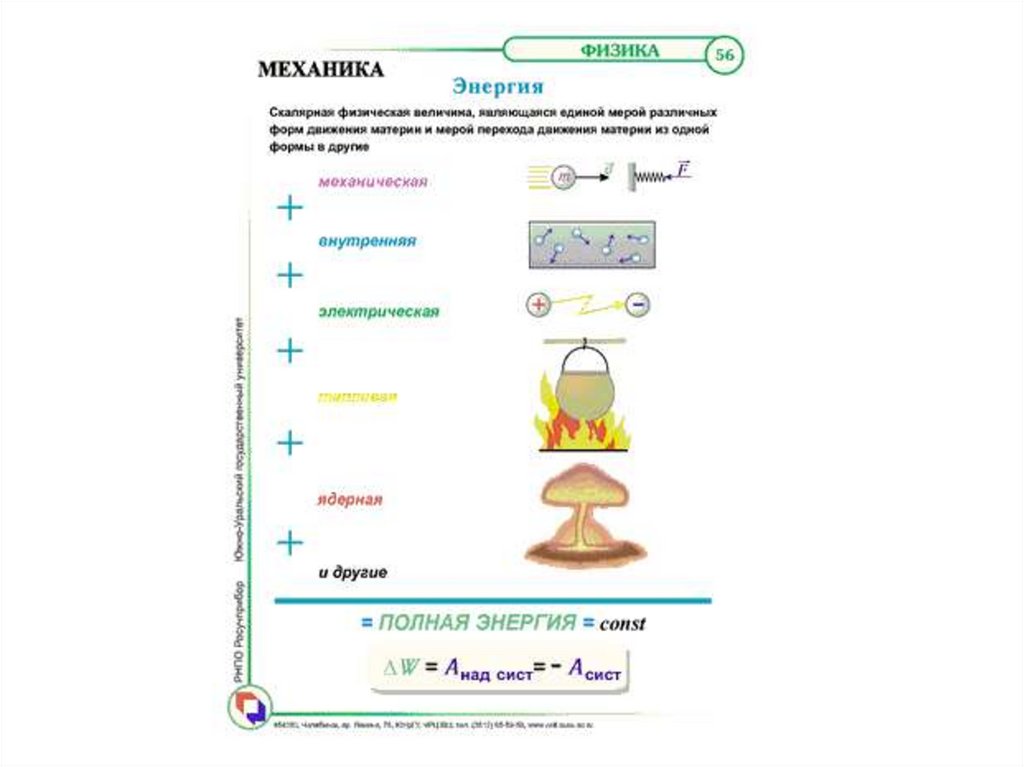
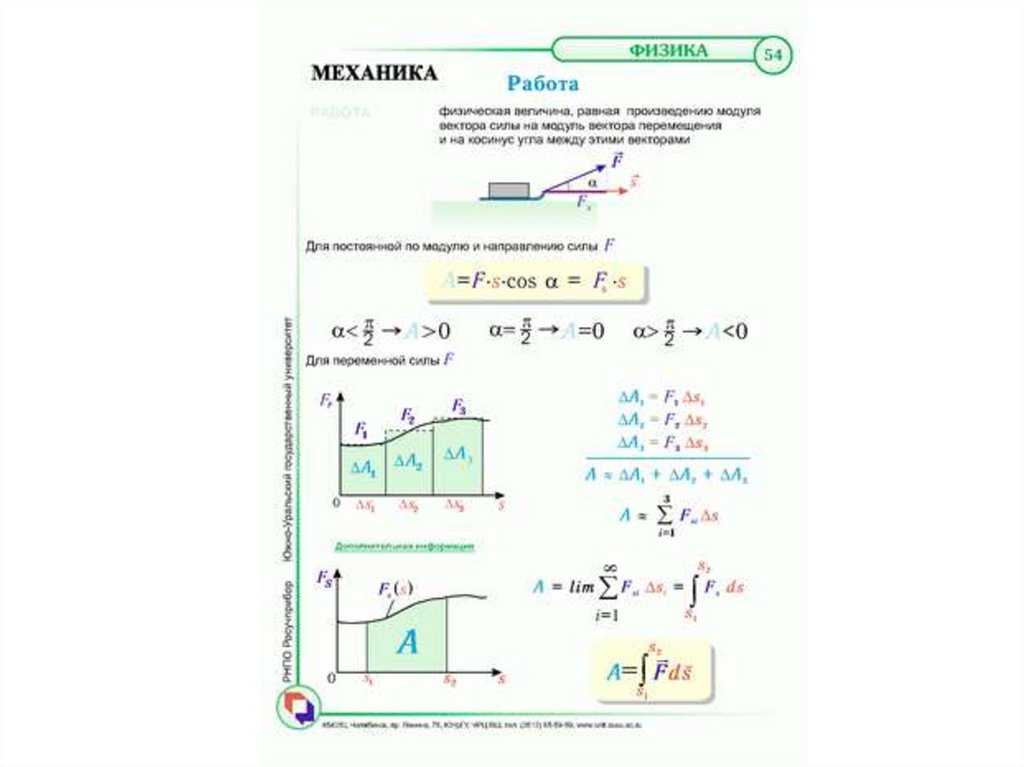
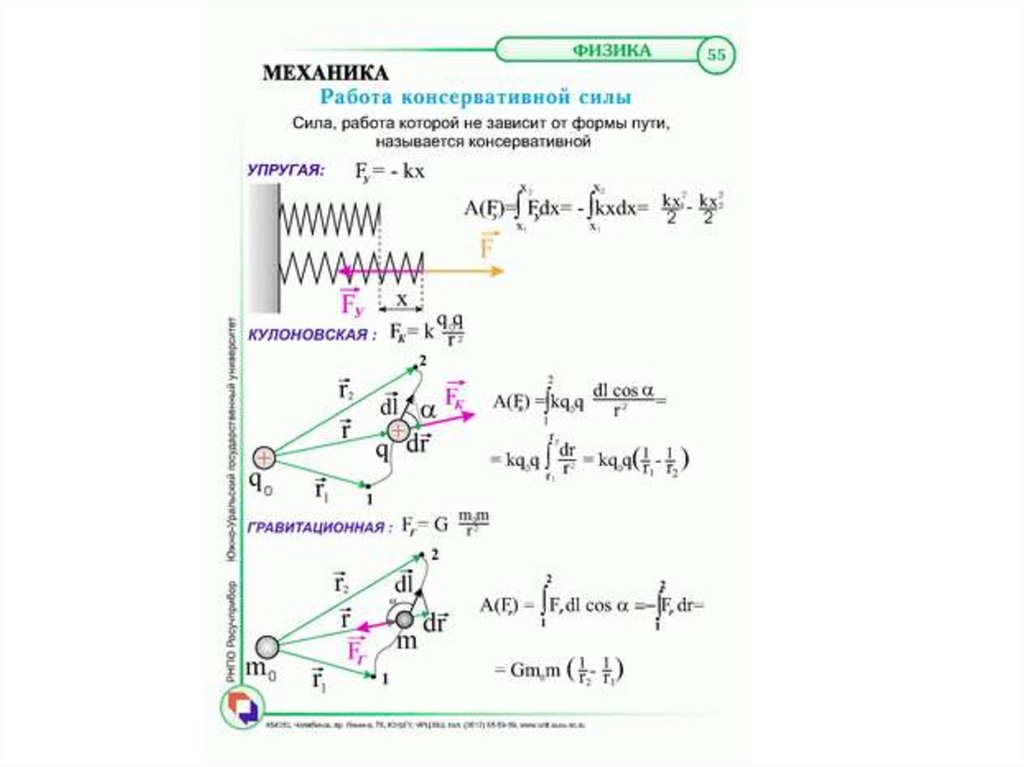
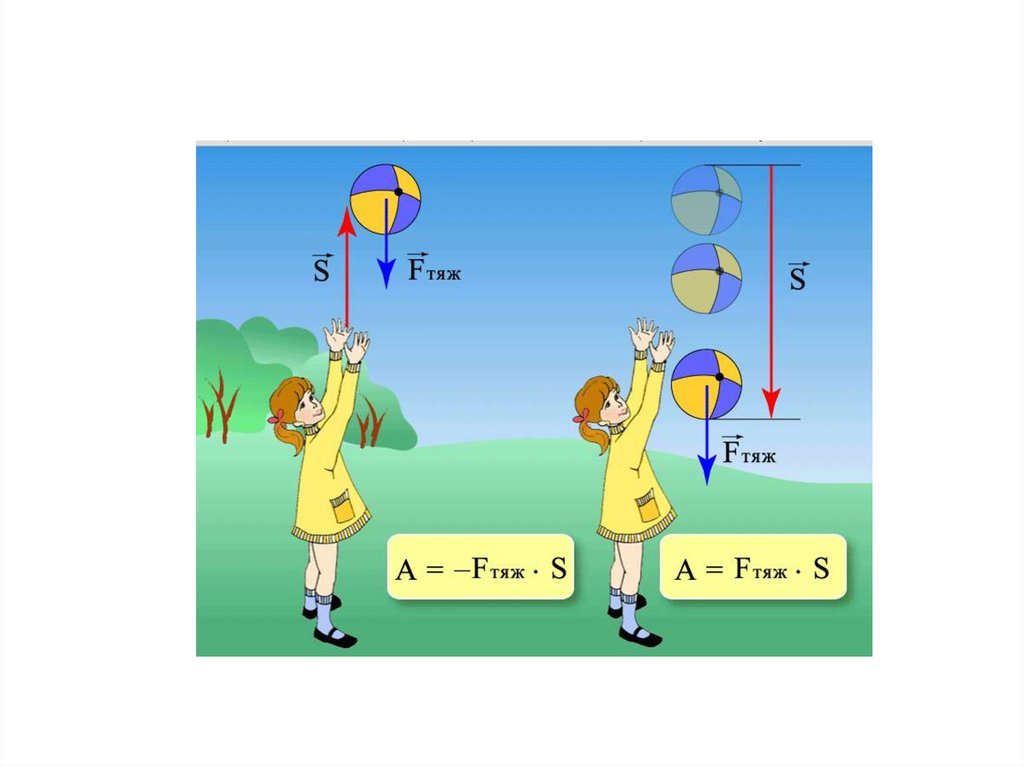
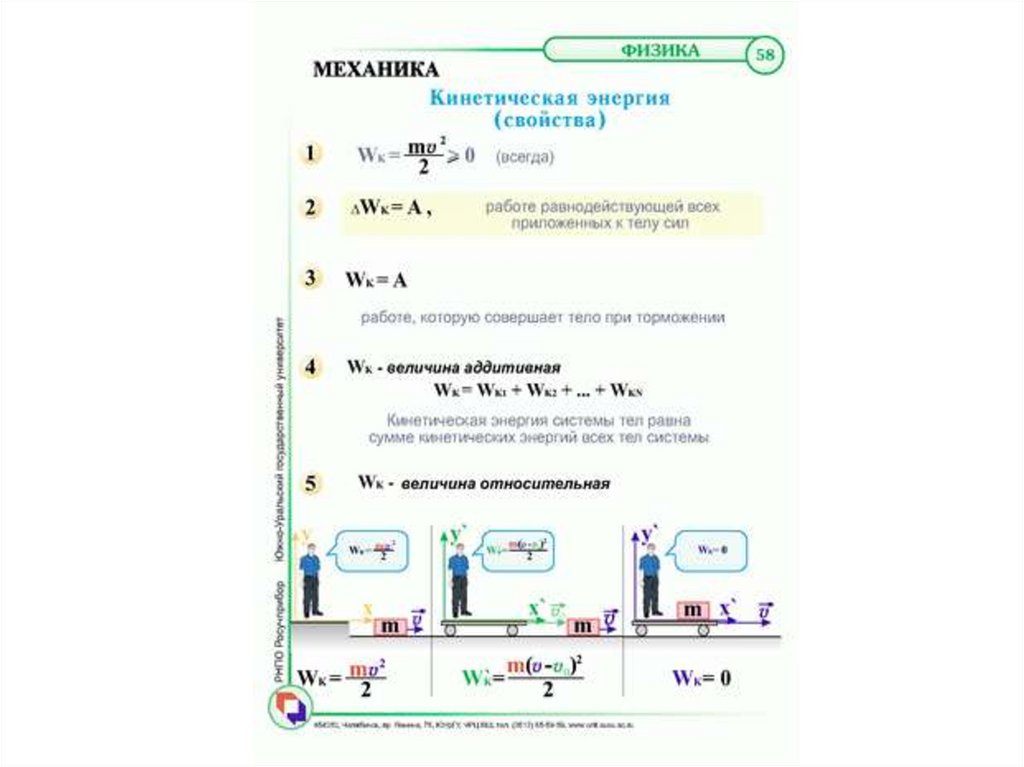
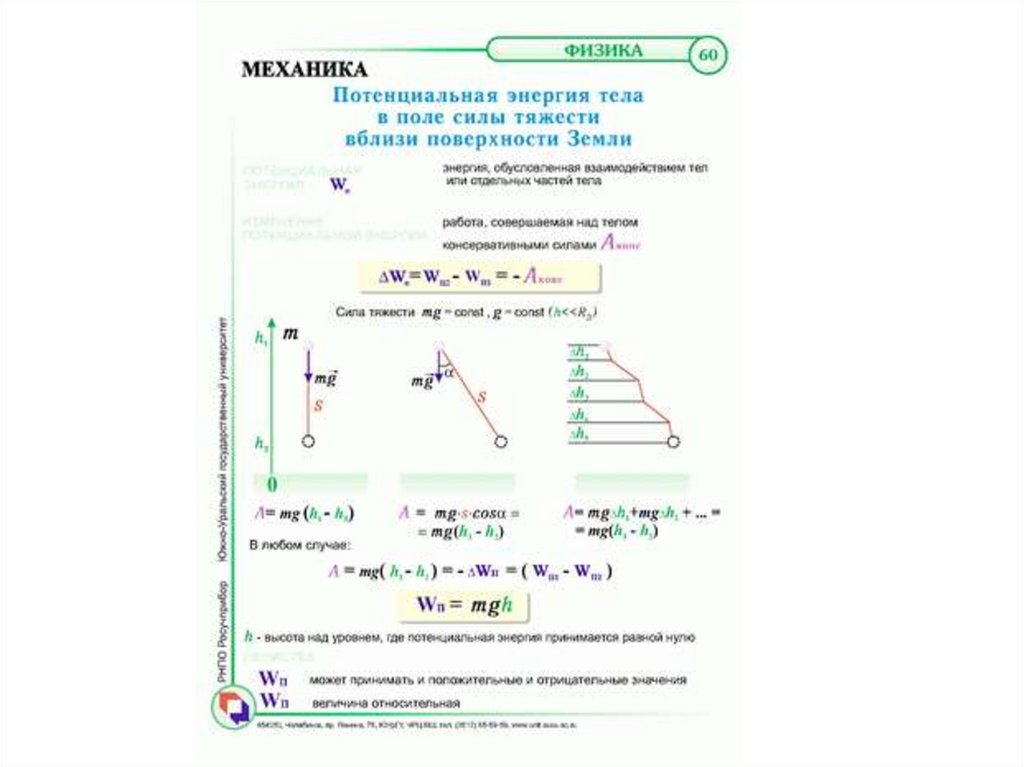
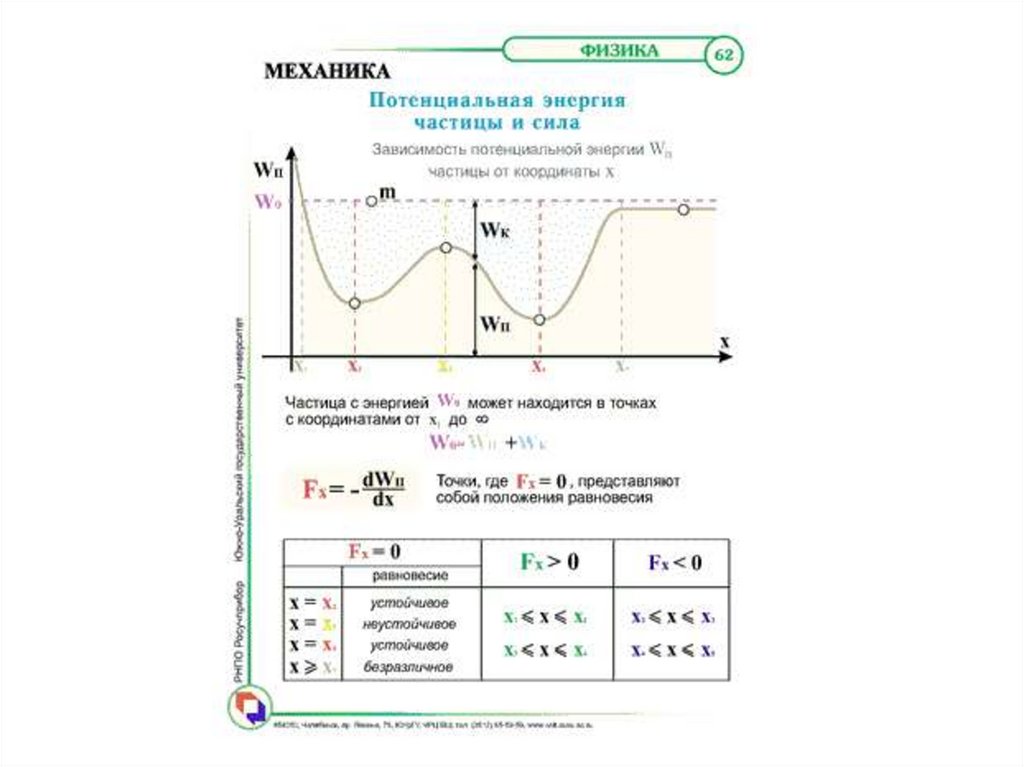
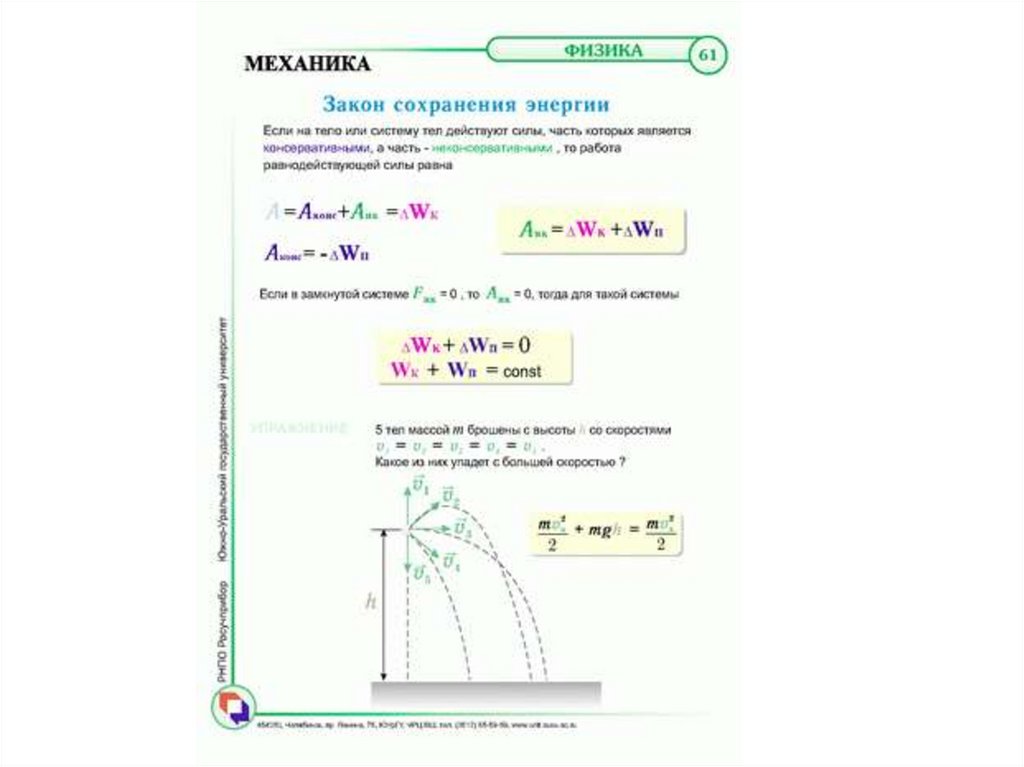
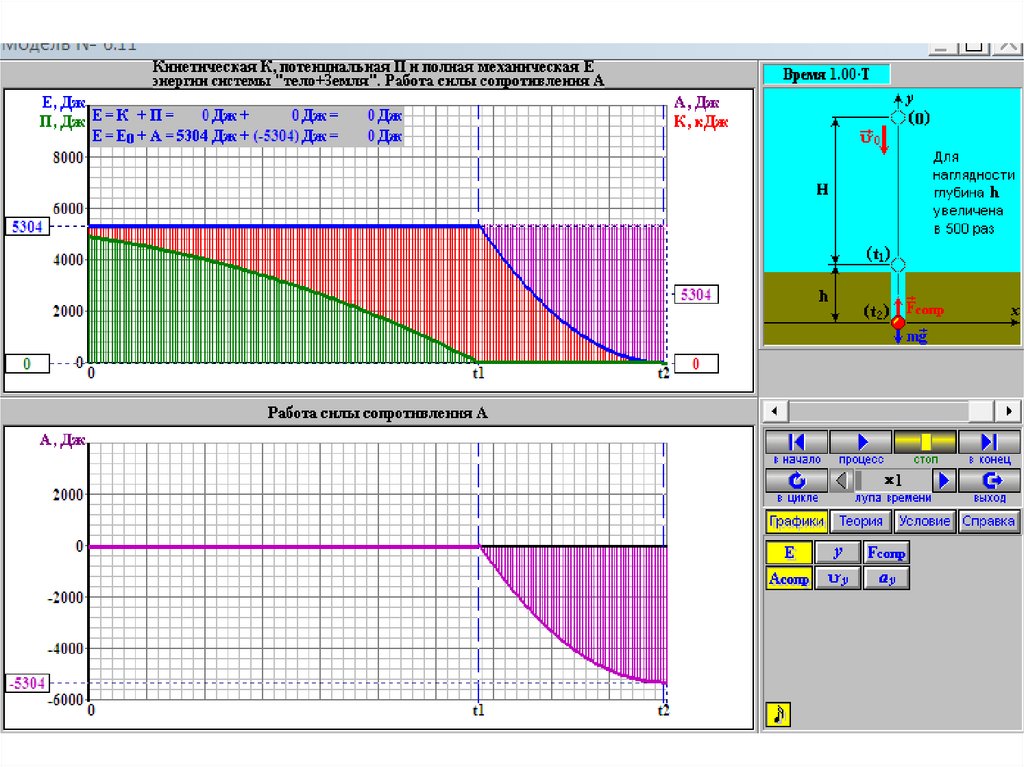
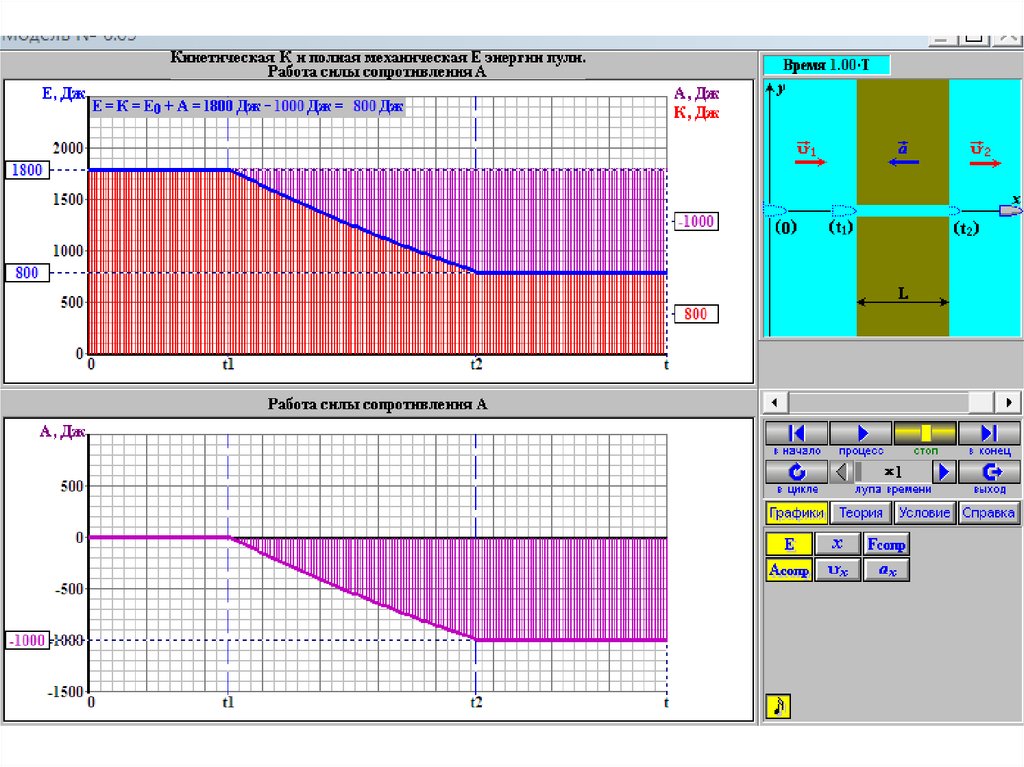
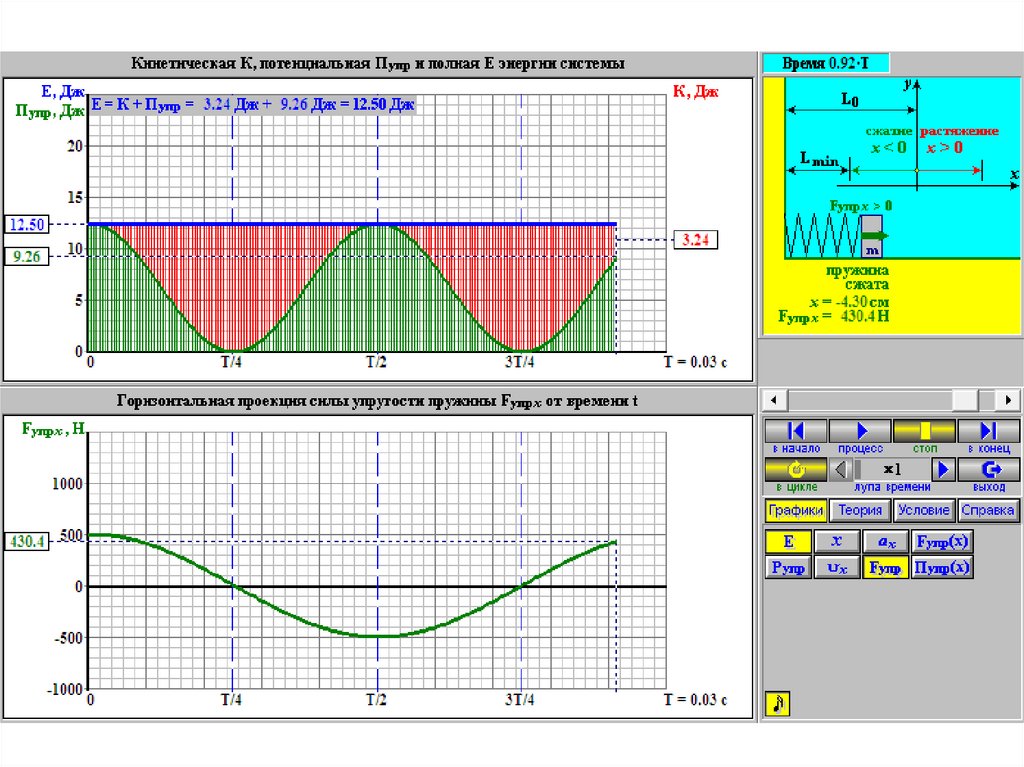
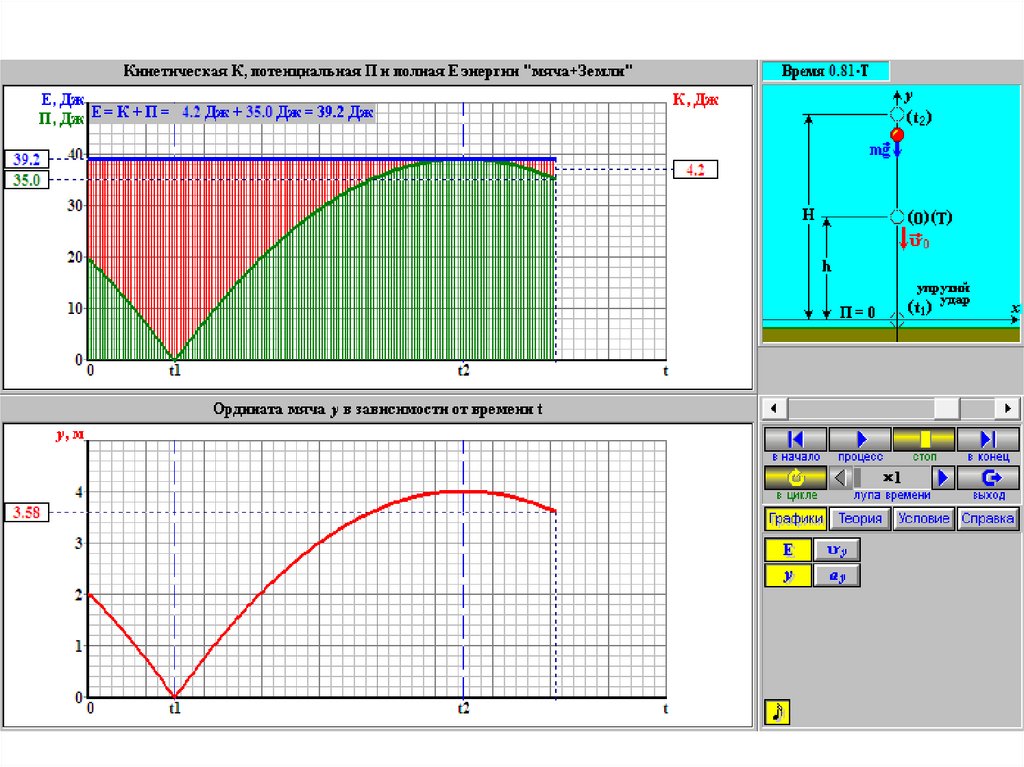
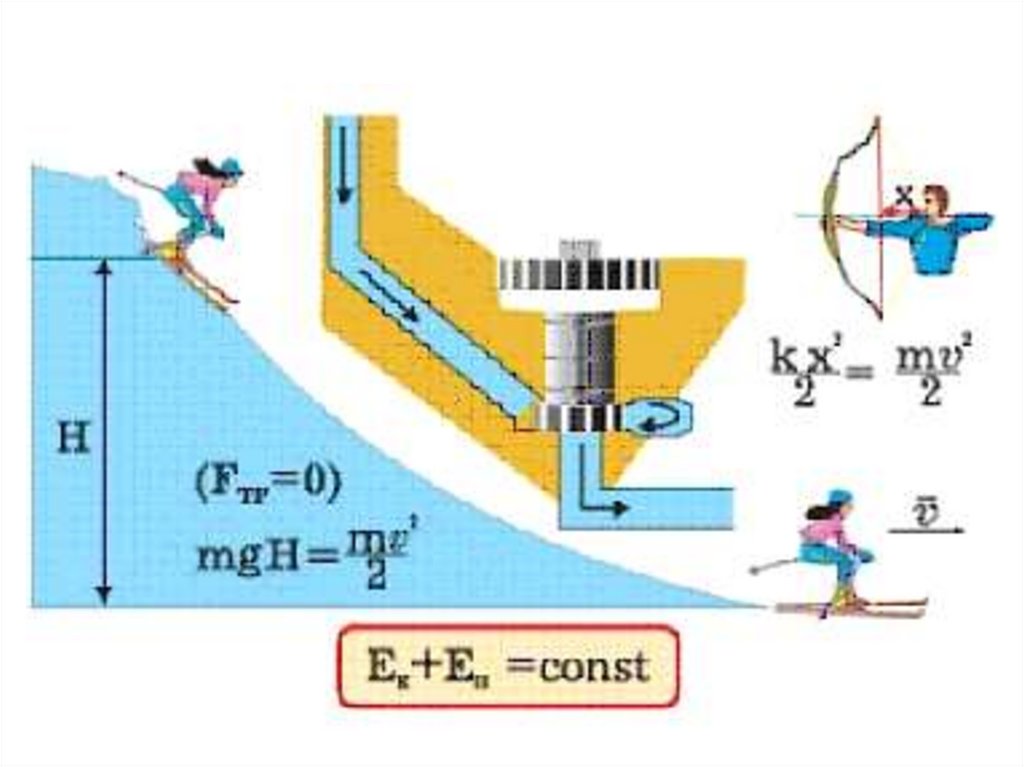
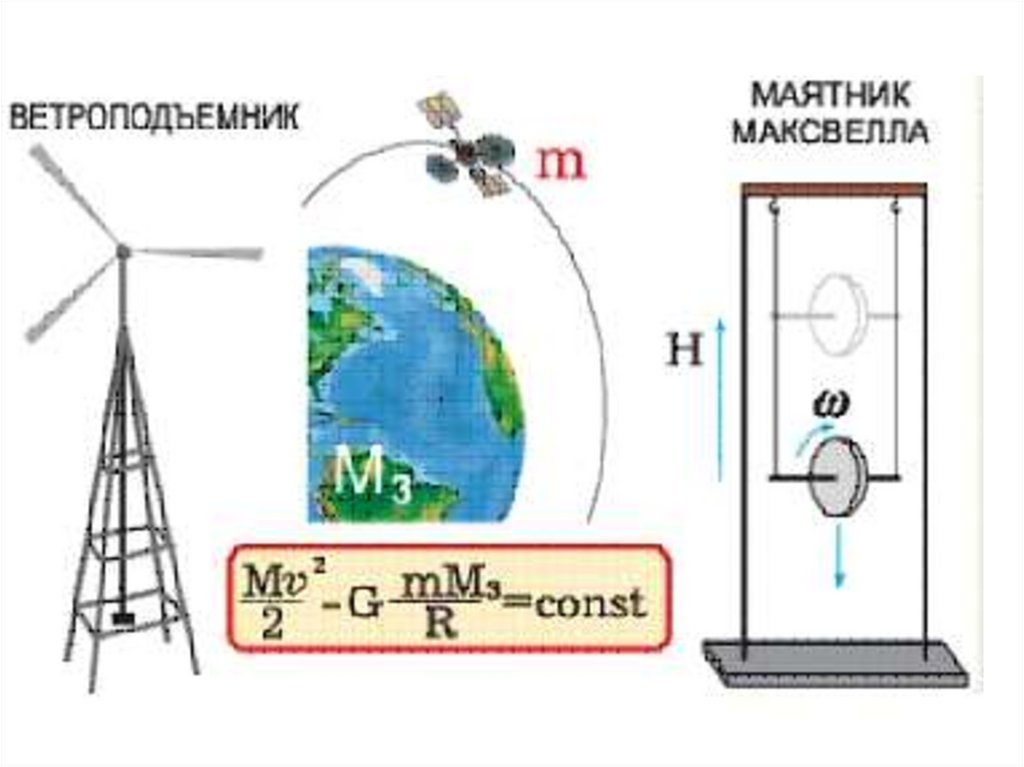
64. Лекция 3. Работа и энергия
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
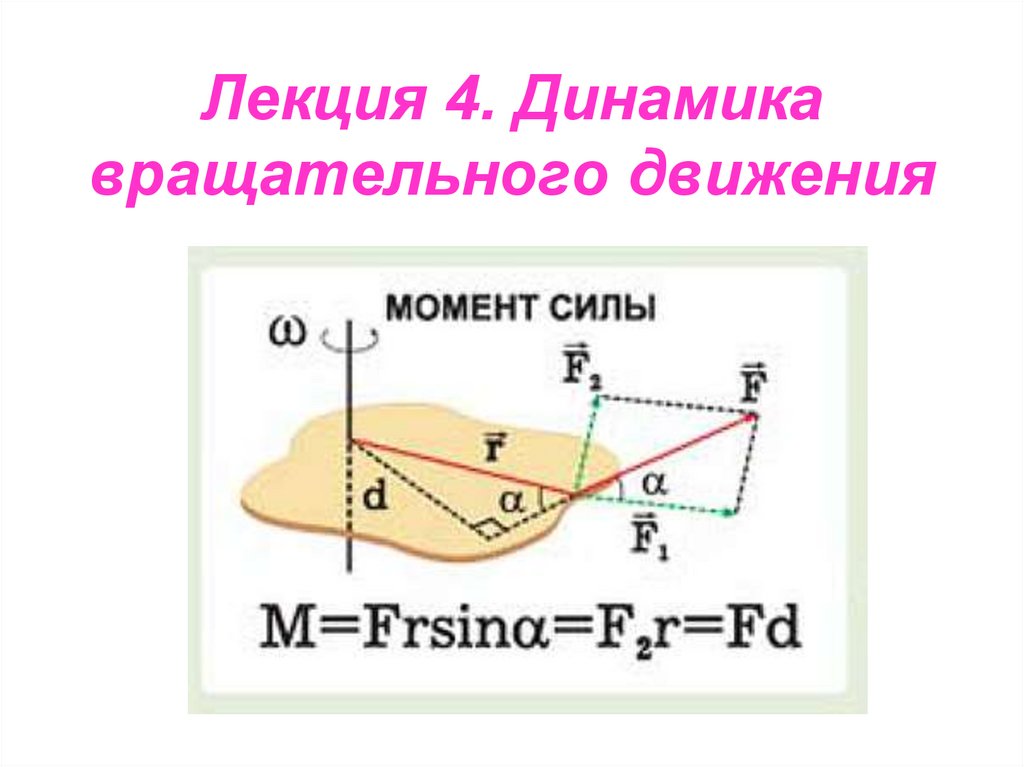
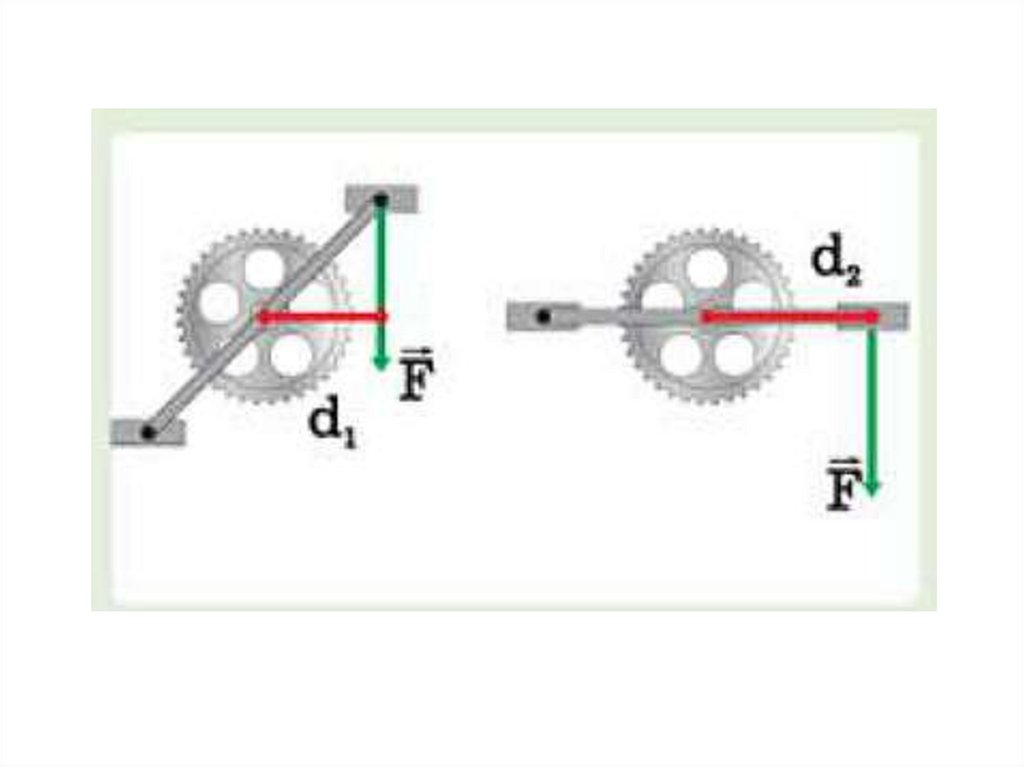
80. Лекция 4. Динамика вращательного движения
81.
82.
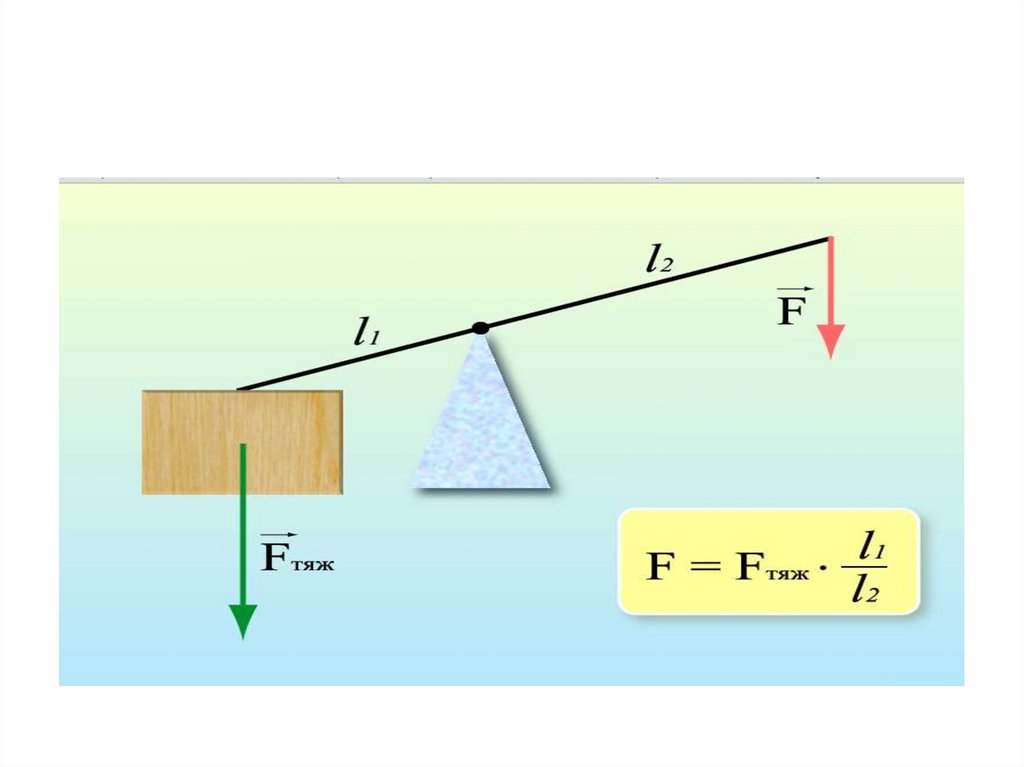
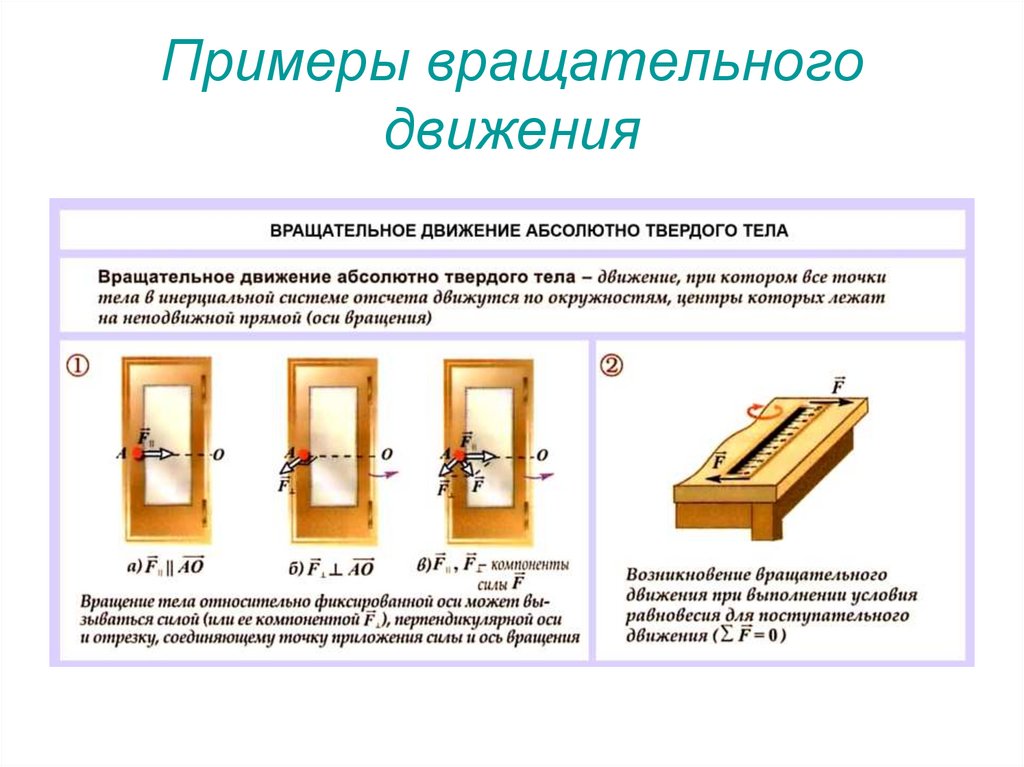
83. Примеры вращательного движения
84.
85.
86.
87.
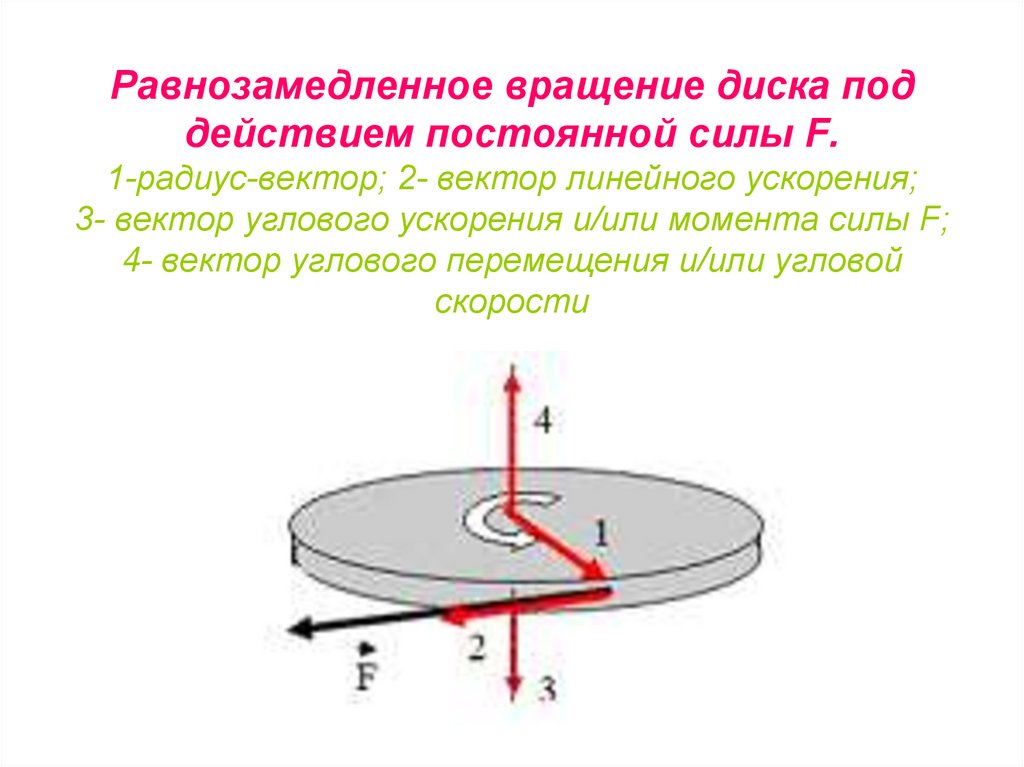
88. Равнозамедленное вращение диска под действием постоянной силы F. 1-радиус-вектор; 2- вектор линейного ускорения; 3- вектор
углового ускорения и/или момента силы F;4- вектор углового перемещения и/или угловой
скорости
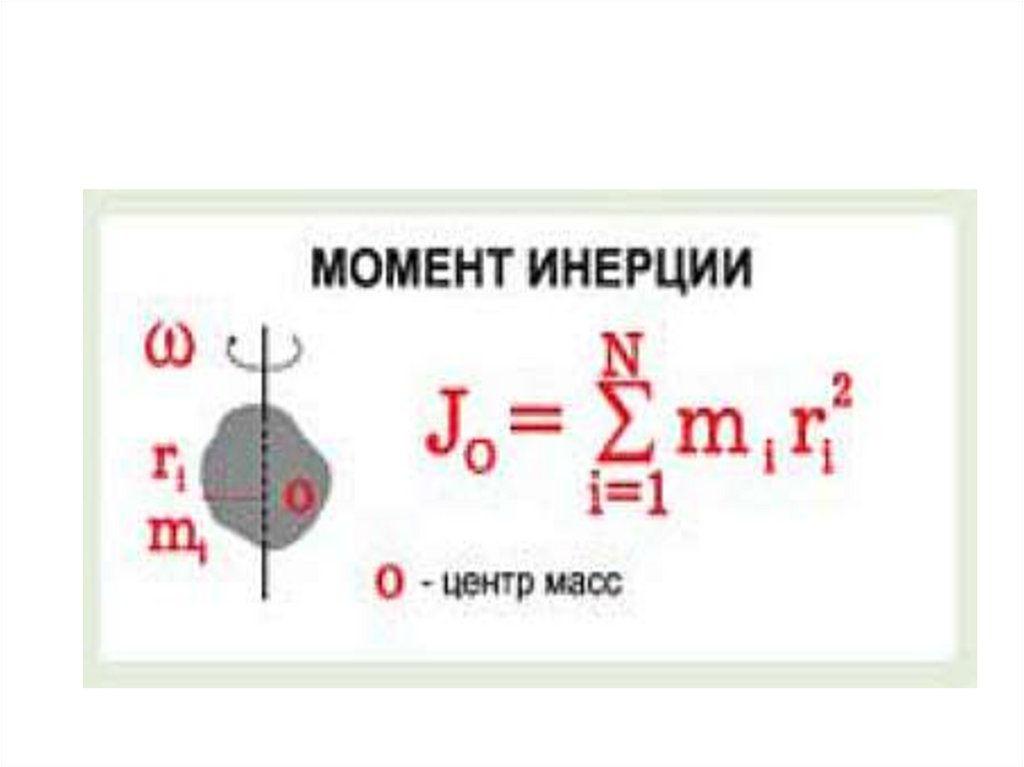
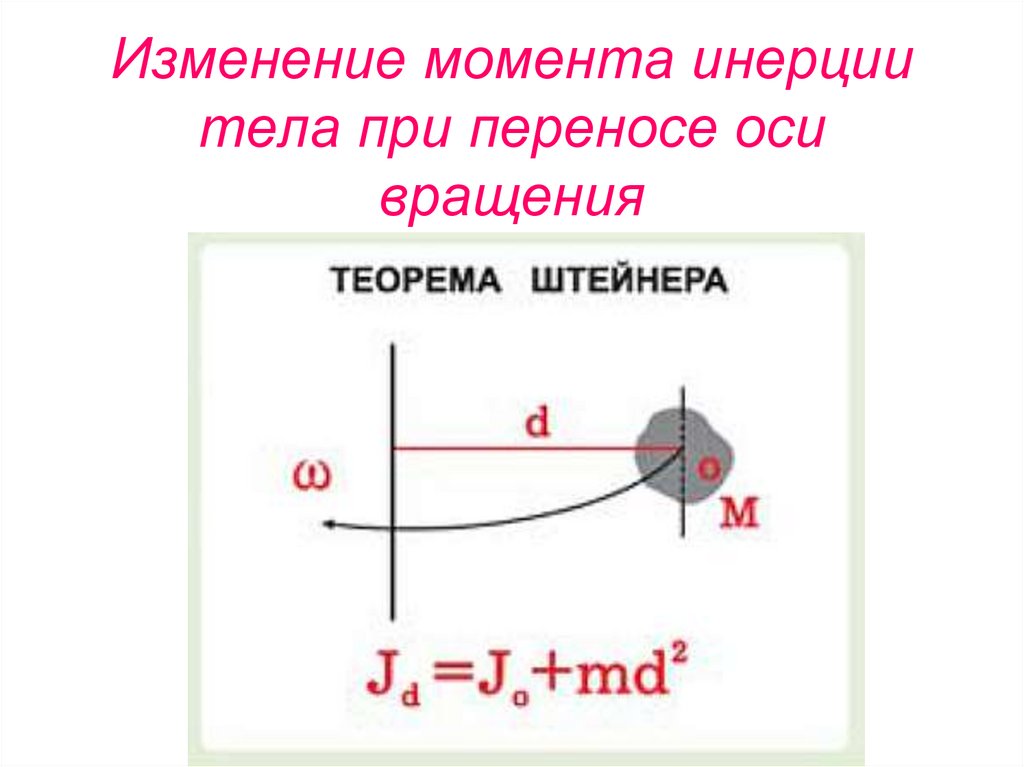
89. Изменение момента инерции тела при переносе оси вращения
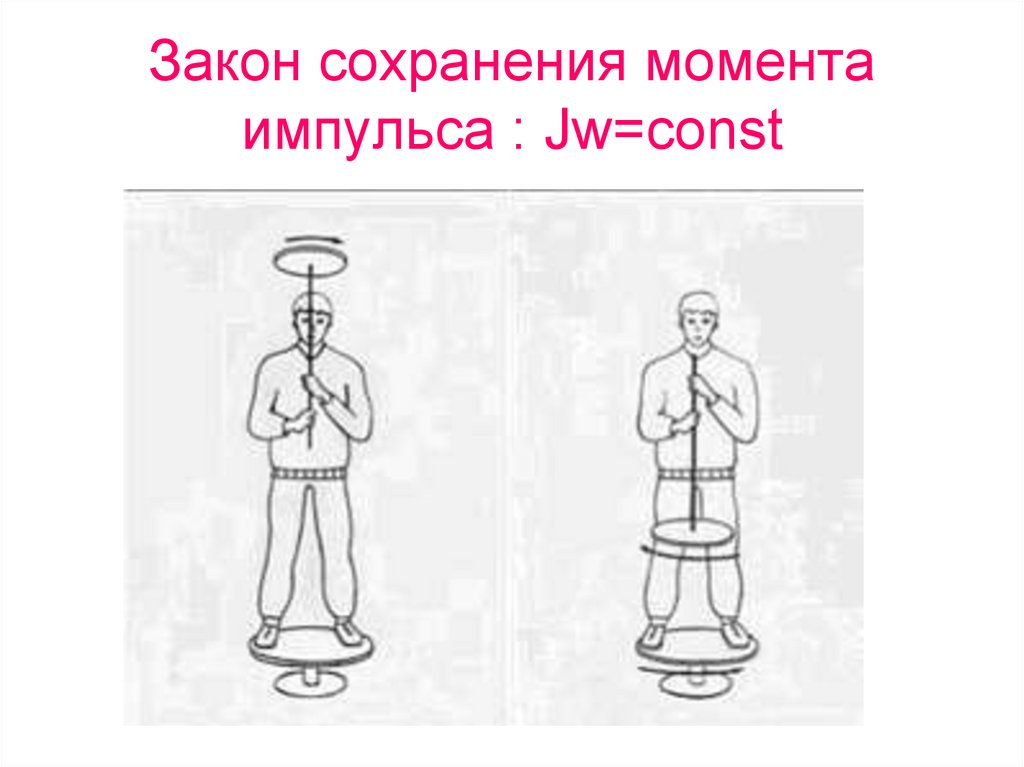
90. Закон сохранения момента импульса : Jw=const
91.
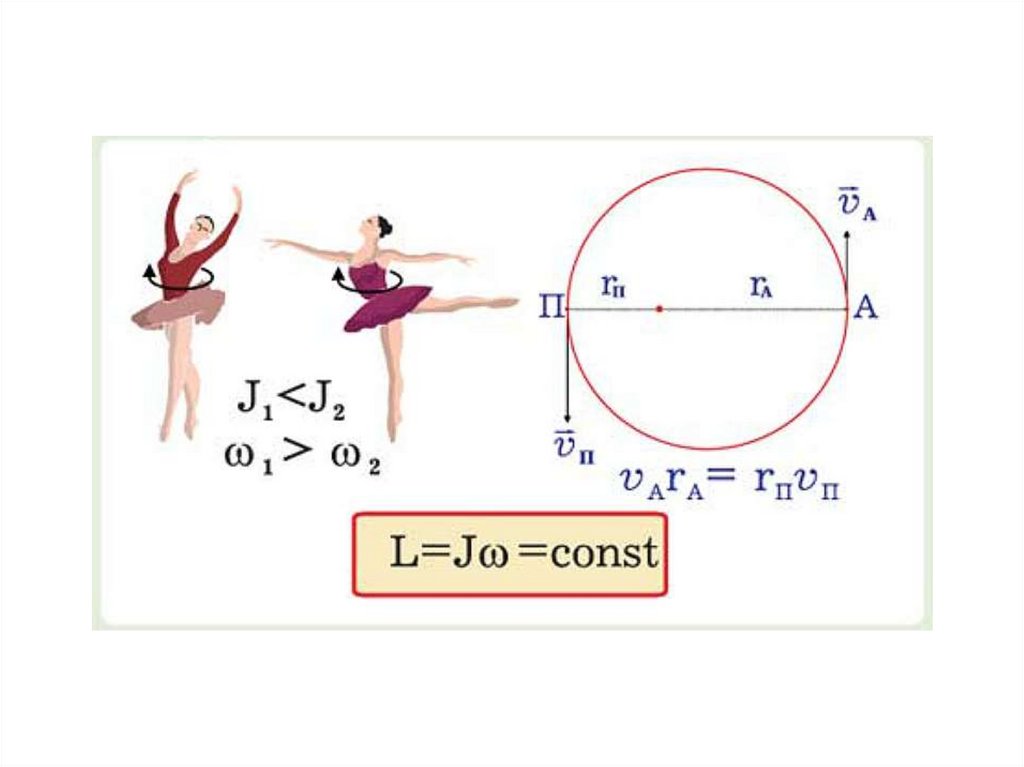
92. Закон сохранения момента импульса : Jw=const
93. Закон сохранения момента импульса : Jw=const
94.
95.
96.
97.
98.
99.
100.
101. Лекция 5 Специальая теория относительности (СТО) (рассматривается только инерциальные системы отсчета)
102. Свойства симметрии пространства и времени
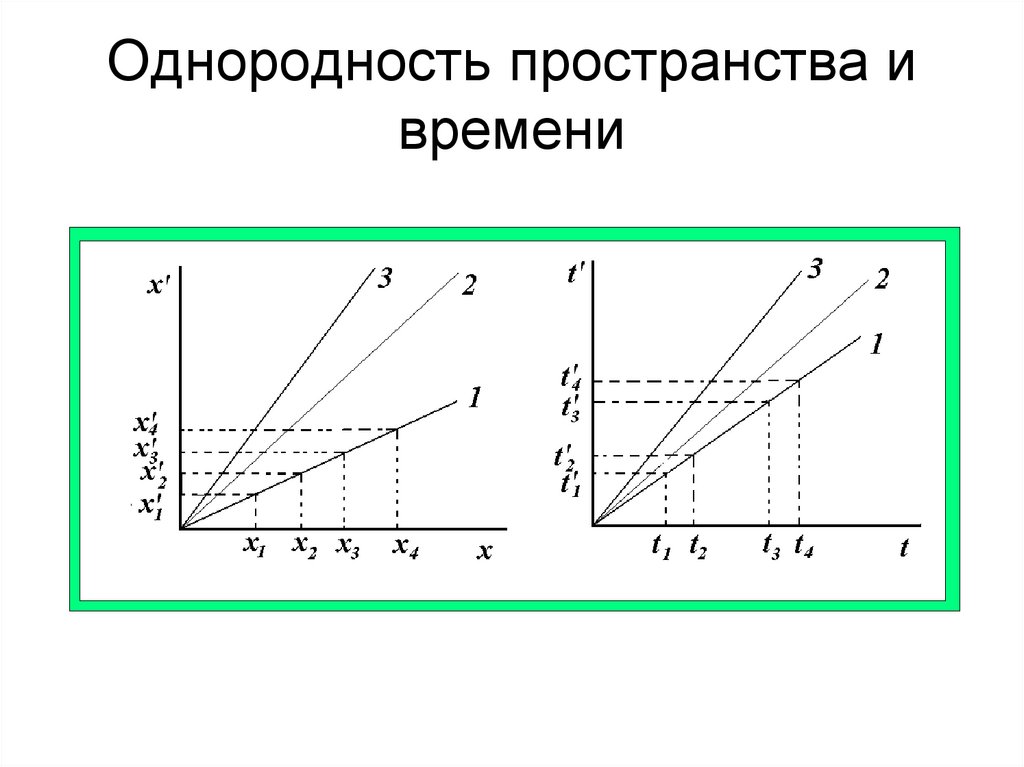
• Однородность и изотропность пространствазаключаются в том, что свойства
пространства одинаковы в различных точках
(однородность), а в каждой точке одинаковы во
всех направлениях (изотропность);
• Однородность времени заключается в том,
что протекание физических явлений(в одних и
тех же условиях) в разное время их наблюдения
одинаково
103. Однородность пространства и времени
104. Общая теория относительности (ОТО) (неинерциальные системы отсчета)
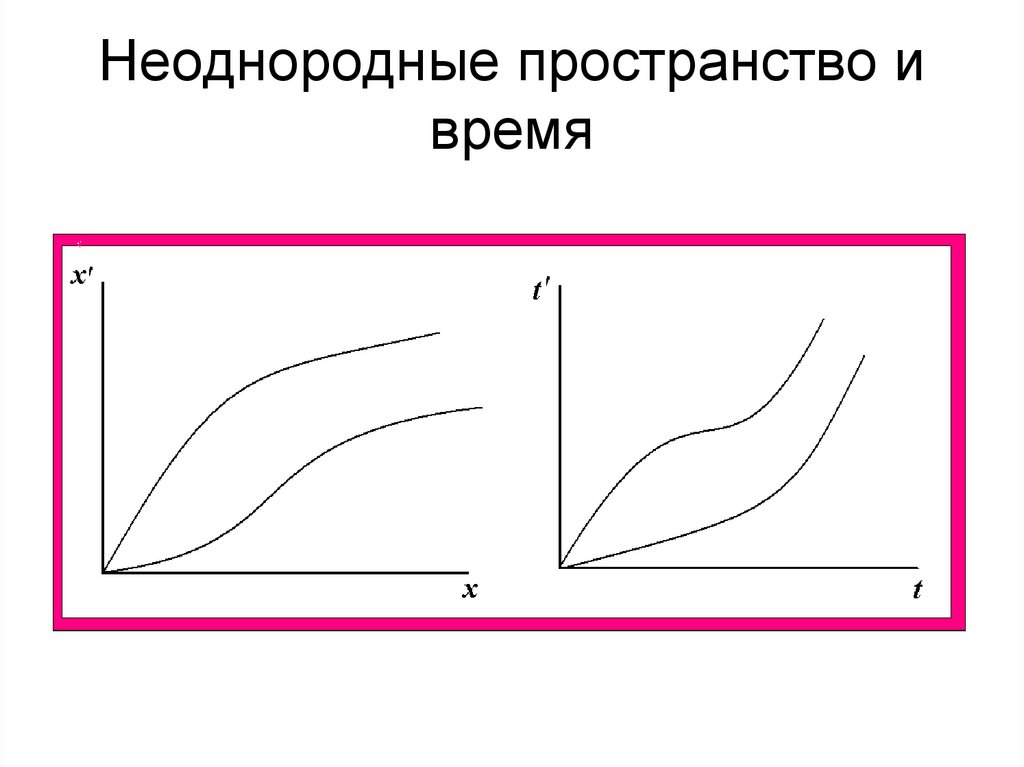
• По отношению к неинерциальнымсистемам отсчета пространство
является неоднородным и неизотропным,
время - неоднородным.
105. Неоднородные пространство и время
106.
107.
108.
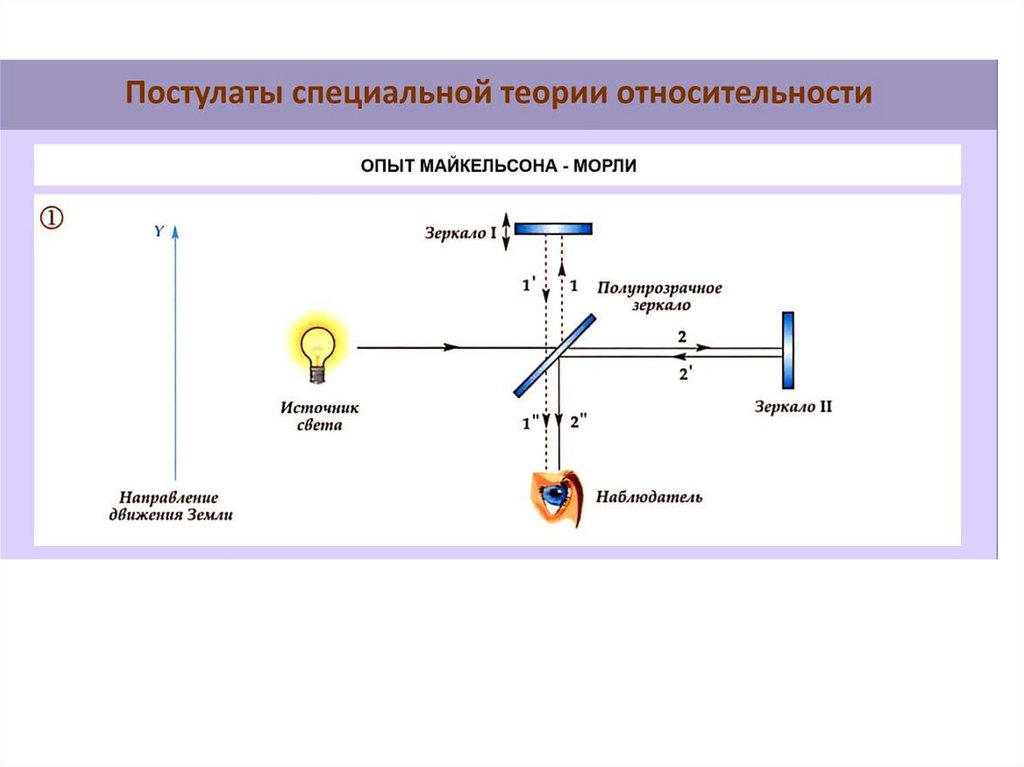
109. Постулаты СТО
• 1 Принцип относительности (всеинерциальные системы отсчета
эквивалентны по своим физическим
свойствам)
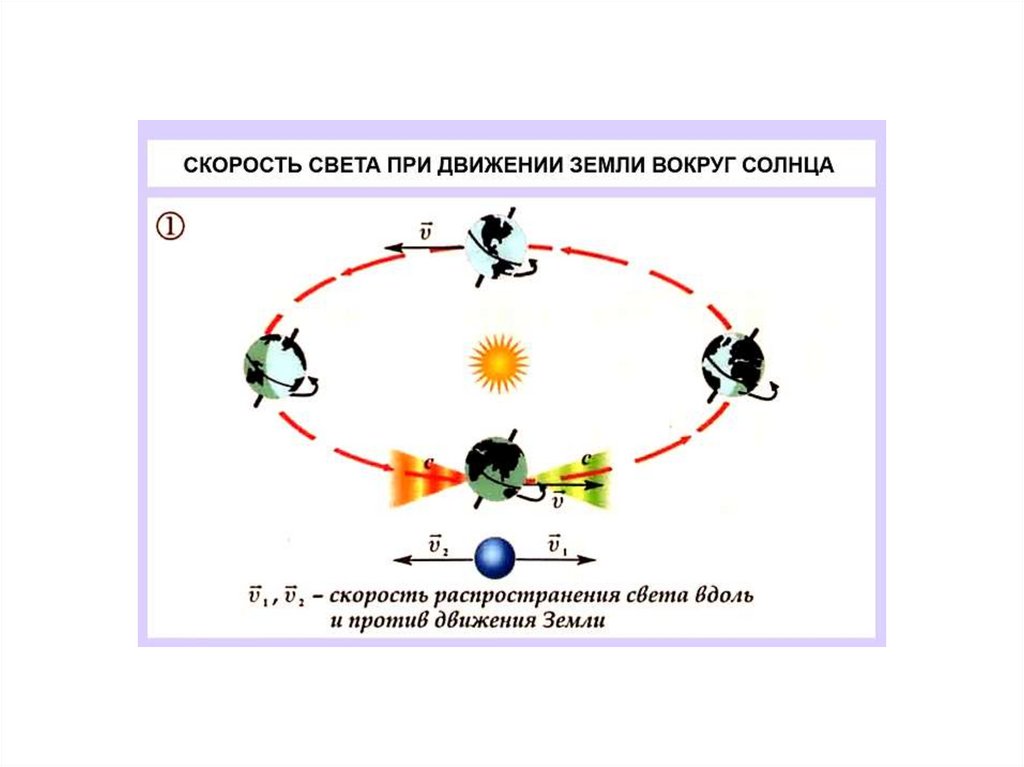
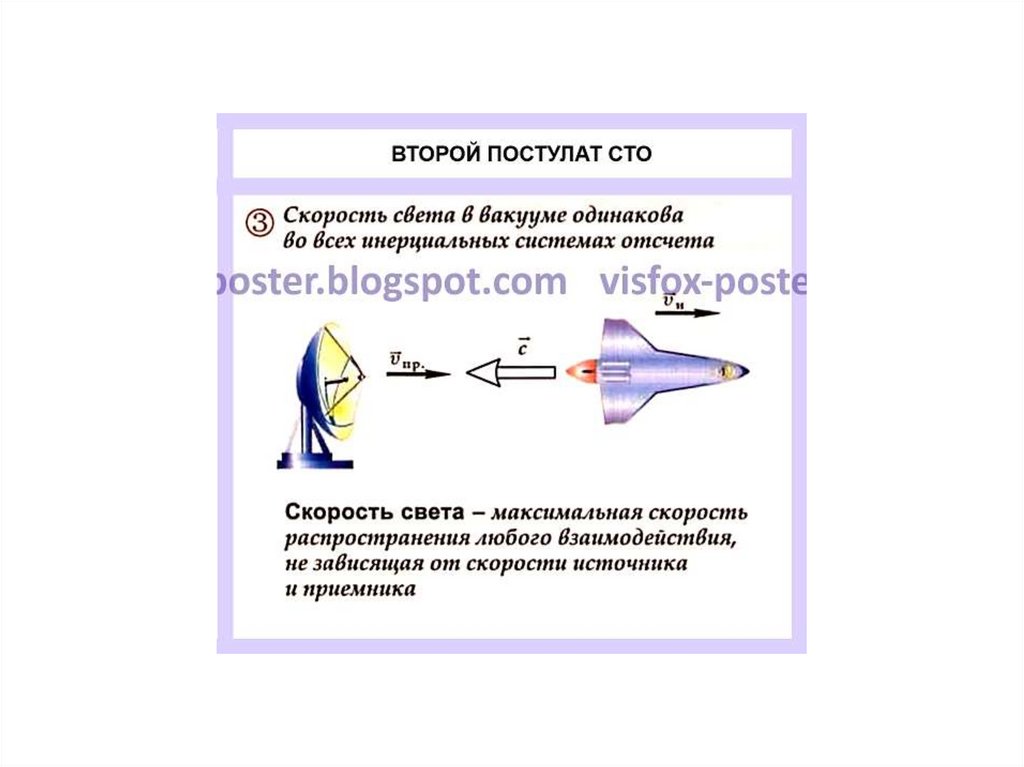
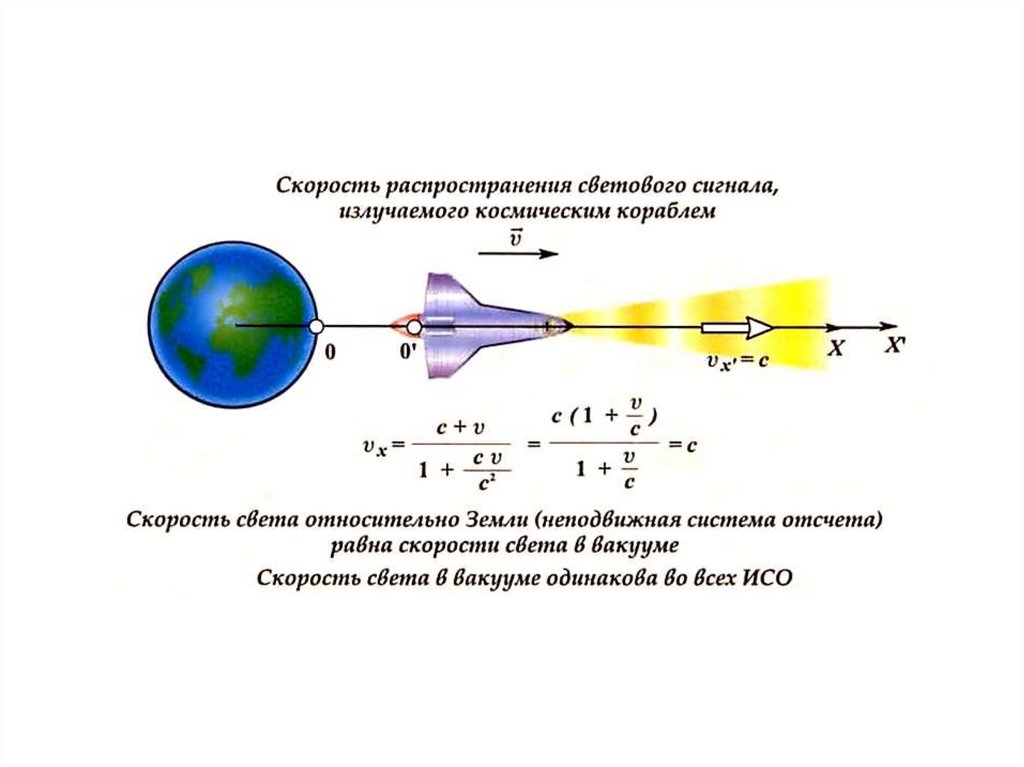
• 2 Независимость скорости света от
скорости источника (скорость света в
вакууме одинакова во всех
инерциальных системах отсчета)














































 Физика
Физика








