Признаки параллелограмма

1.

Признаки
параллелограмма

2.

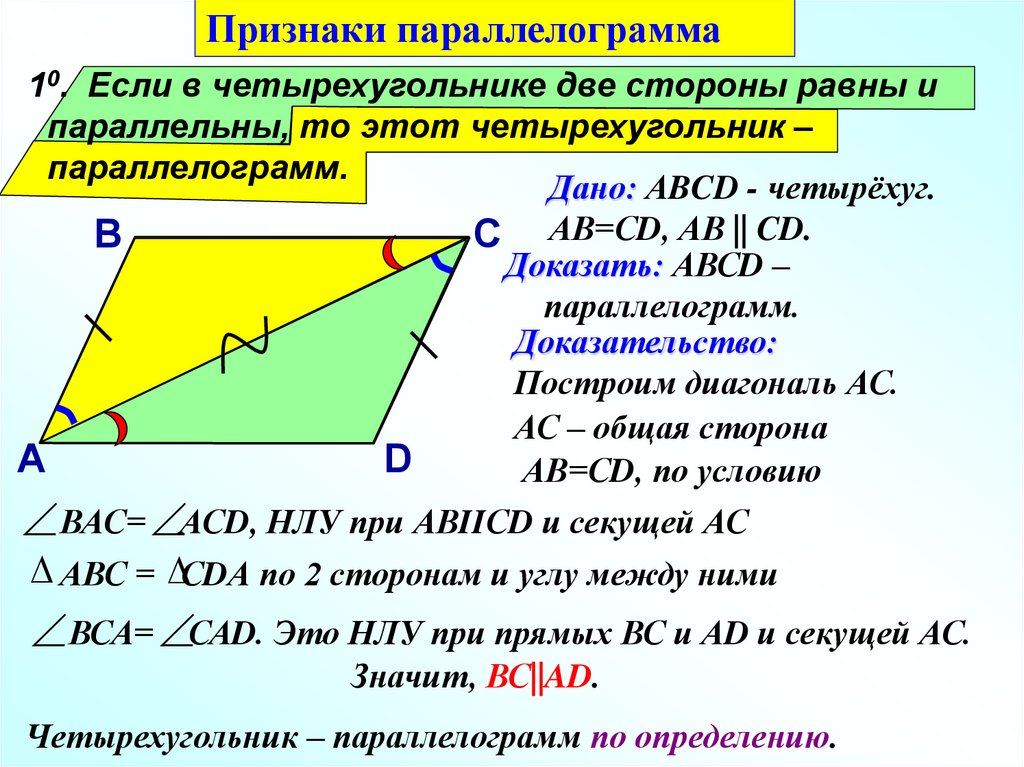
Признаки параллелограмма
10. Если в четырехугольнике две стороны равны и
параллельны, то этот четырехугольник –
параллелограмм.
Дано: АBCD - четырёхуг.
В
С АВ=СD, АВ || CD.
Доказать: АВСD –
параллелограмм.
Доказательство:
Построим диагональ АС.
АС – общая сторона
А
D
АВ=СD, по условию
ВАС= АСD, НЛУ при АВIIСD и секущей АС
АВС = СDА по 2 сторонам и углу между ними
ВСА= САD. Это НЛУ при прямых ВС и АD и секущей АС.
Значит, ВС||AD.
Четырехугольник – параллелограмм по определению.

3.

Признаки параллелограмма
20. Если в четырехугольнике противоположные
стороны попарно равны, то этот четырехугольник –
параллелограмм.
Дано: АВ=СD, ВС=АD.
В
А
С Доказать: АВСD –
параллелограмм.
Доказательство:
Построим диагональ АС.
АС – общая сторона
АВ=СD, по условию
D
ВС=АD, по условию
АВС = СDА по трем сторонам
ВАС= АСD. Это НЛУ при прямых АВ и СD и секущей АС.
Значит, АВ||СD.
АВ=СD, по условию.
Четырехугольник – параллелограмм по признаку 10.

4.

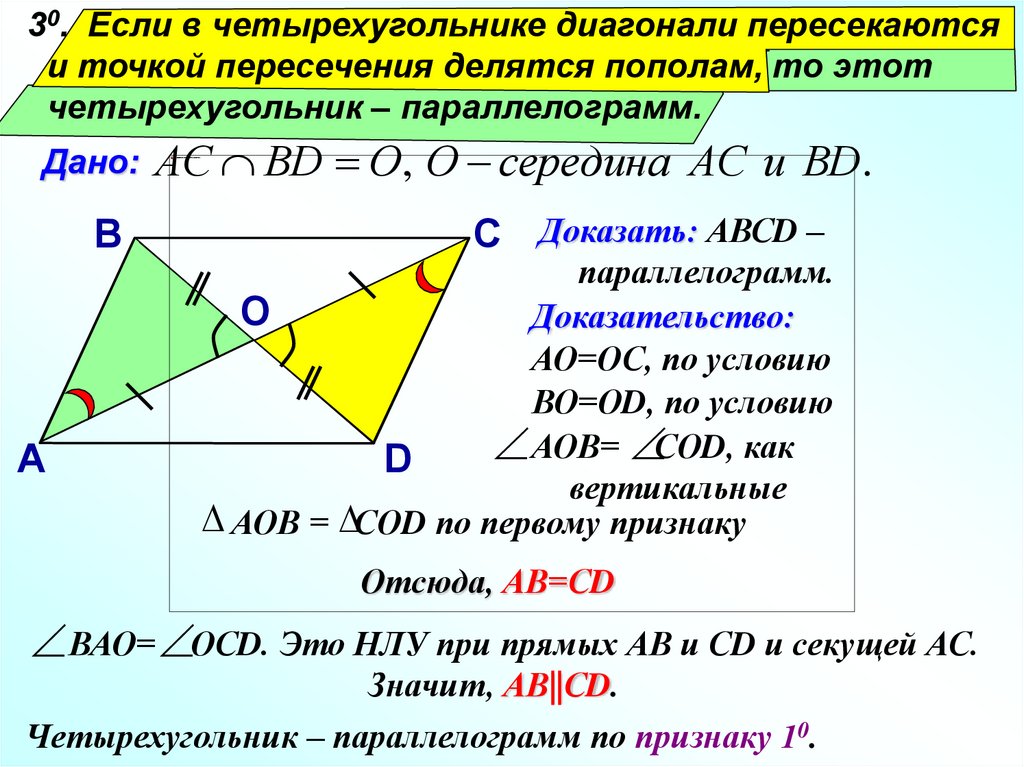
30. Если в четырехугольнике диагонали пересекаются
и точкой пересечения делятся пополам, то этот
четырехугольник – параллелограмм.
Дано:
В
А
АС ВD О, О середина АС и ВD.
С Доказать: АВСD –
параллелограмм.
О
Доказательство:
АО=ОС, по условию
ВО=ОD, по условию
АОВ= СОD, как
D
вертикальные
АОВ = СОD по первому признаку
Отсюда, АВ=СD
ВАО= ОСD. Это НЛУ при прямых АВ и СD и секущей АС.
Значит, АВ||СD.
Четырехугольник – параллелограмм по признаку 10.