Похожие презентации:
Законы сохранения
1. ЗАКОНЫ СОХРАНЕНИЯ
2. СОХРАНЯЮЩИЕЕСЯ ВЕЛИЧИНЫ
3. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И РАБОТА
4.
5.
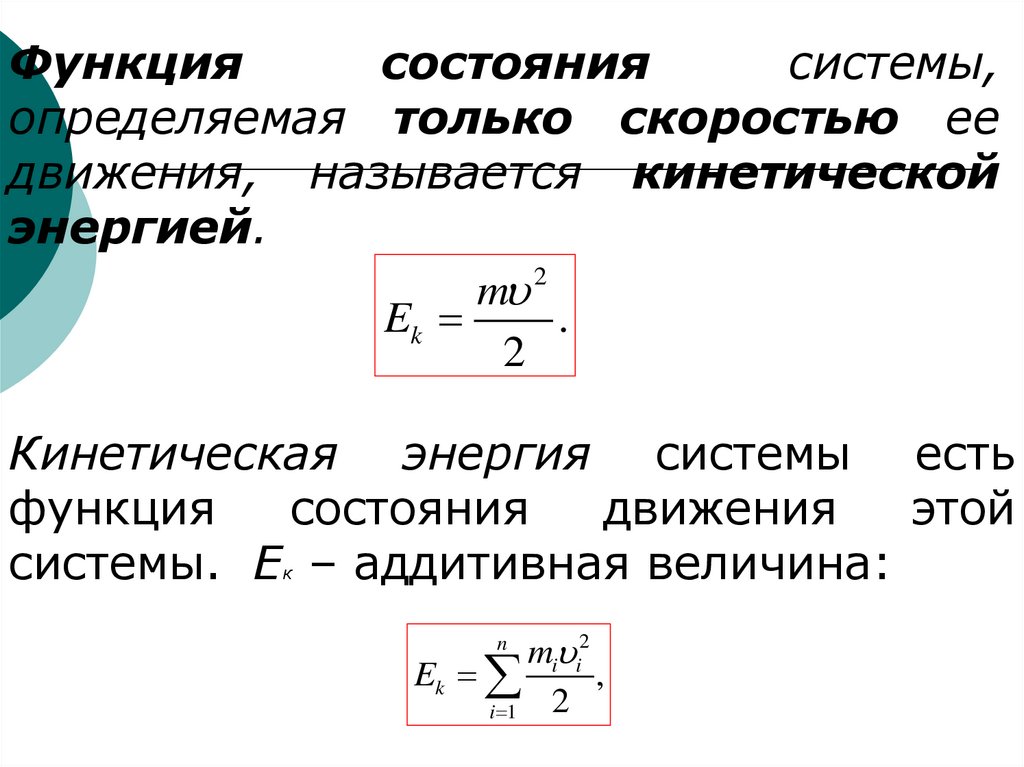
Функциясостояния
системы,
определяемая только скоростью ее
движения, называется кинетической
энергией.
m 2
Ek
.
2
Кинетическая энергия системы есть
функция
состояния
движения
этой
системы. Е – аддитивная величина:
к
mi i2
Ek
,
2
i 1
n
6.
Связь кинетической энергии симпульсом p.
m m m
,
2 m 2m
2
Т.к.
2
2
p
Ek
.
2m
2
отсюда
7.
Связь кинетической энергии сработой.
Если постоянная сила действует на
тело, то оно будет двигаться в
направлении силы. Тогда,
элементарная работа по перемещению
тела из т. 1 в т. 2, будет равна
произведению силы F на перемещение
dr :
dA Fdr
2
A Fdr Ek 2 Ek1.
1
8.
Следовательно,работа
силы
приложенной к телу на пути r численно
равна
изменению
кинетической
энергии этого тела:
A Ek .
Или
изменение
кинетической
энергии dK равно работе внешних
сил:
dEk dA.
9.
Скорость совершения работы (передачиэнергии) называется мощность.
Мощность есть работа, совершаемая
в единицу времени.
dA
Мгновенная
мощностьN
dt
d
r
или
N F F .
dt
A
Средняя мощность N
.
t
10. Консервативные силы и системы
Кроме контактных взаимодействий,наблюдаются взаимодействия между
телами, удаленными друг от друга.
Подобное
взаимодействие
осуществляется
посредством
физических полей (особая форма
материи).
Каждое тело создает вокруг себя
поле, которое проявляет себя именно
воздействием на другие тела.
11.
Силы, работа которых не зависит отпути, по которому двигалось тело, а
зависит от начального и конечного
положения
тела
называются
консервативными.
Обозначим A – работа консервативных
сил, по перемещению тела из т. 1 в т. 2
12.
A1a 2 A1b 2 A1l 2 A12 .Изменение направления движения
на
противоположное
–
вызывает
изменение знака работы консервативных
сил.
Отсюда
следует,
что
работа
консервативных сил вдоль замкнутой
кривой равна нулю:
Fdr A
12
L
A21 A12 A12 0
13.
Если циркуляция какого-либо векторасилы
равна
нулю,
то
эта
сила
консервативна.
Консервативные
силы:
сила
тяжести,
электростатические силы, силы центрального
стационарного поля.
Неконсервативные силы: силы трения, силы
вихревого электрического поля.
Консервативная система – такая, внутренние
силы которой только консервативные, внешние
– консервативны и стационарны.
14. Потенциальная энергия
Если на систему материальных телдействуют консервативные силы, то
можно
ввести
понятие
потенциальной энергии.
Работа,
совершаемая
консервативными
силами
при
изменении конфигурации системы, не
зависит от того как было осуществлено
это изменение. Работа определяется
только
начальной
и
конечной
конфигурациями системы:
15.
A U U ,12
1
2
Потенциальная энергия U (х, у, z) – функция
состояния системы, зависящая только от
координат
всех
тел
системы
в
поле
консервативных сил.
Работа консервативных
потенциальной энергии:
сил
dA dU .
равна
убыли
16.
Потенциальная энергия пригравитационном взаимодействии
Или
Работа тела при падении
A U U .
A mgh.
0
Условились
считать,
что
поверхности
земли (h 0),
U
тогда
U A
т.е.
U mgh.
на
0
0
17.
Дляслучая
гравитационного
взаимодействия между массами M и
m, находящимися на расстоянии r
друг
от
друга,
потенциальную
энергию можно найти по формуле:
Mm
U G
.
r
18.
Потенциальная энергия упругойдеформации (пружины)
Найдём работу, совершаемую при
деформации упругой пружины.
F kx,
Сила
упругости
Сила
непостоянна,
поэтому
элементарная работа
упр
dA Fdx kxdx
знак минус говорит о том, что работа
совершенна над пружиной.
kx kx
A dA kxdx
,
2
2
x2
x1
2
2
1
2
19.
Т.е. A U 1тогда
U
2
Примем:U 2
kx
U
.
2
2
0, U U
1
20. Закон сохранения механической энергии
Закон сохранения сводит воединорезультаты, полученные нами раньше.
В сороковых годах девятнадцатого
века трудами Р. Майера, Г. Гельмгольца
и Дж. Джоуля (все в разное время и
независимо друг от друга) был доказан
закон
сохранения
и
превращения
энергии.
21.
Для консервативной системы частицможно найти полную энергию системы:
E K U
внутр.
U
внеш .
const
Для
механической
энергии
закон
сохранения
звучит
так:
полная
механическая энергия консервативной
системы материальных точек остаётся
постоянной.
22.
Для замкнутой системы, т.е. для системына которую не действуют внешние силы,
можно записать:
E K U
внутр.
const
т.е.
полная
механическая
энергия
замкнутой системы материальных точек, между
которыми действуют только консервативные
силы, остаётся постоянной.
23.
Если в замкнутой системе действуютнеконсервативные
силы,
то
полная
механическая энергия системы не сохраняется
– частично она переходит в другие виды
энергии – неконсервативные.
Система, в которой механическая энергия
переходит в другие виды энергии, называется
диссипативной,
сам
процесс
перехода
называется диссипацией энергии.

























 Физика
Физика








