Похожие презентации:
Закон сохранения энергии в механике
1. Лекция № 4
ЗАКОН СОХРАНЕНИЯЭНЕРГИИ В МЕХАНИКЕ
2. Работа и мощность силы
элементарномРабота силы F на
перемещении d r точки приложения силы
(рис. 4.1):
1
r1
O
dr
F
r2 2
Рис. 4.1
В СИ A = [Дж]
A F d r cos
(4.1)
Элементарная работа
(4.2)
A F , d r
Дж Н м
3.
Работа переменной силыдвижении вдоль траектории L
A F,d r
F
при
(4.3)
L
Работа внешних сил при повороте тв.
тела вокруг неподвижной оси z на угол φ:
A M z d
(4.4)
0
Mz– результирующий момент внешних сил,
действующих
на
тело,
относительно
неподвижной оси.
4.
Мощность– это работа, совершаемая
силой F за единицу времени
A
dr
F
P
F
(4.5)
dt
dt
В СИ P = [Вт]
A
Pcp
t
Средняя мощность
Работа, которую совершает сила за
промежуток времени t:
t
t
(4.6)
A F d t P d t
0
0
5. Кинетическая энергия
Кинетическая энергия является мероймеханического движения материи.
Кинетическая энергия МТ и тела при
его поступательном движении
m
p
Ek
2
2m
2
2
(4.7)
N
p pi
i 1
6.
Кинетическая энергия МС – суммакинетических энергий отдельных точек
системы
N
N m 2
i i
Ek сист . E ki
i 1
i 1
2
(4.8)
где Eki, mi и υi – соответственно кинетическая
энергия, масса и скорость i-ой МТ. В СИ
Ek Дж
Кинетическая
энергия
–
всегда
положительная величина, обращающаяся в
нуль лишь при одновременном равенстве нулю
скоростей всех точек системы.
7.
Поступательное движение (υi = υc).Ek
2
M c
(4.9)
2
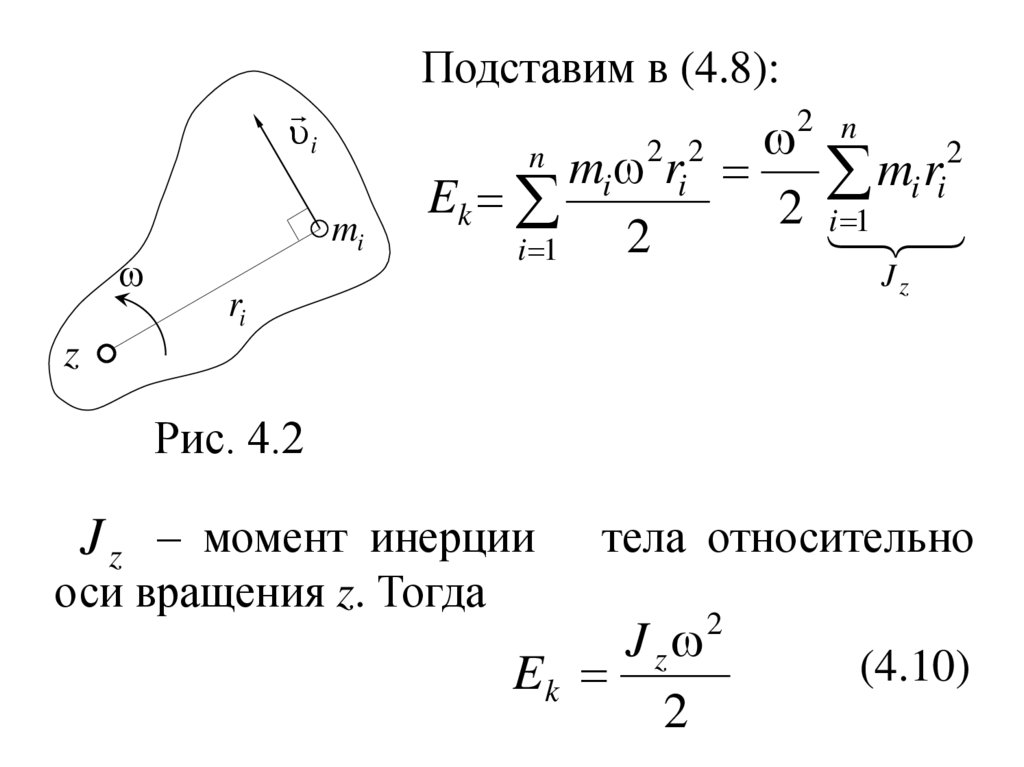
Кинетическая энергия вращательного
движения тв.тела, вращающегося вокруг оси
z с угловой скоростью ω (рис. 4.2)
i ri
где ri – расстояние от точки до оси z.
8.
Подставим в (4.8):i
n
mi
Ek
i 1
2 2
mi ri
2
2 n
mi ri
2
2
i 1
Jz
ri
z
Рис. 4.2
J z – момент инерции
оси вращения z. Тогда
тела относительно
J z
Ek
2
2
(4.10)
9. Работа и кинетическая энергия
Для МТ при m = const из (2.4):d
ma m
F
dt
a
2
d d m
F
m
dt dt 2
F P
– мощность силы.
10.
С учетом (4.5) и (4.7)d Ek
P
dt
dt
d Ek P d t F
dr
первая производная по времени от
кинетической энергии точки – мощность
действующей на точку силы.
d Ek F d r
d E k A
(4.11)
11. Консервативные силы
Если в каждой точке пространства напомещенную туда частицу действует сила, то
частица находится в поле сил.
Поле, остающееся постоянным во
времени – стационарное. В нём сила,
действующая на частицу, зависит только от
ее положения. Стационарное поле в одной
СО может оказаться нестационарным в
другой СО.
Силы поля консервативные
(потенциальные), если в стационарном
случае их работа на любом замкнутом пути
равна нулю.
12.
Работа в потенциальном полеНайдем работу сил
поля при перемещении
2 частицы из т. 1 в т. 2 через т.
O (рис. 4.3).
1
O
Рис. 4.3
2
A12 F d r
1
(4.12)
E p1 E p 2 E p
Здесь Ep убыль потенциальной энергии.
13. Связь между потенциальной энергией и консервативной силой
СоотношениеA F d r d E p
(4.13)
d E p Fx d x Fy d y Fz d z
d Ep
E p
x
dx
E p
y
dy
E p
z
dz
(4.14)
(4.15)
14.
Приравниваем левые части (4.14) и (4.15)Fx d x Fy d y Fz d z
(4.16)
E p
x
dx
E p
y
dy
E p
z
dz
15.
FxE p
, Fy
x
E p1 E p 2 E p 3 E p 4
grad E p
A
F
E p1 E p 2 E p 3 E p 4
E p
y
, Fz
E p
z
.
(4.17)
Связь между
потенциальной
энергией и
консервативной силой
(рис. 4.4):
F grad E p
(4.18)
E p E p E p
grad E p
i
j
k
x
y
z
(4.19)
Рис. 4.4
16. Потенциальные энергии тяготения и упругих деформаций
Потенциальная энергия тяготения.Гравитационная сила притяжения двух МТ
задается законом всемирного тяготения
Ньютона:
mm r
Fтяг . 2
r r
(4.20)
Силы гравитационного притяжения –
центральные консервативные.
17.
mmE p
r
(4.21)
Потенциальная энергия МТ, массы m,
находящейся
на
высоте
h
над
поверхностью Земли:
E p mgh C
С – потенциальная энергия на нулевом
уровне. Пусть С = 0, тогда
E p mgh
18.
Потенциальная энергия растянутойпружины. Упругие силы, возникающие при
медленных
деформациях
пружины
–
центральные, консервативные:
Fупр. kx
Растяжение пружины x = l – l0, разность ее
длин
в
деформированном
(l)
и
недеформированном (l0) состояниях.
19.
Привозвращении
пружины
из
деформированного в недеформированное
состояние сила Fупр. совершает работу
x
0
kx 2
A Fупр. d x k x d x
2
0
x
Если считать потенциальную энергию в
недеформированном состоянии равной нулю,
то энергия деформированной пружины
kx
Ep
2
2
(4.22)
20. Закон изменения и сохранения механической энергии системы n материальных точек
Полная механическая энергия системыE Ek E p
(4.23)
если между точками системы действуют
только консервативные силы.
21.
Если система замкнута, т.е. Aвнешн . 0 E 0E const
(4.24)
Закон
сохранения
полной
механической энергии в ИСО: полная
механическая энергия замкнутой системы
тел, на которые действуют только
консервативные силы, остается постоянной.
Если между точками системы действуют
неконсервативные силы (силы трения и т.д.)
E E2 E1 Aвнешн . Aнеконс .
22.
Если система замкнута, т.е.а
Aвнешн . 0,
Aнеконс . Aтр . 0
E E 2 E1 0
или
E 2 E1
– диссипация (рассеивание) механической
энергии, переход механической энергии в
тепловую.





















 Физика
Физика








