Закон Кулона. Напряженность поля точечного заряда

1.

Электростатика

2. Закон Кулона. Напряженность поля точечного заряда.

Сила взаимодействия двух точечных зарядов
q1
F12
r
F21
Закон Кулона
q2
F k
F12 q1
q1 q2
r
2
q2 F21
Напряженность электростатического поля
1 )q 0,qnp 0
q
qnp
E
Fnp
E Fnp
1 q1 q2
2
4 0 r
E
Fnp
qnp
q qnp 1
q
1
E
2
2
4 0
r
qnp 4 0 r
1

3.

2 )q 0,qnp 0
E Fnp
q
Fnp
qnp
E
q
1
Напряженность поля точечного заряда E
2
4 0 r
Силовые линии некоторых полей
q 0
q 0
Принцип суперпозиции электрических полей
Ep
Fp
qnp
n
F1 F2 ... Fn
E1 E2 ... En Ei
qnp
i 1

4.

Напряженность электростатического поля
на оси
кольца
dE"
R
dE dE dE
"
E
dE
dE
E dE dE" dE
Из соображений симметрии
dE" dE sin
dE dE cos
x
E" dE sin 0
1 dq
E dE dE cos
cos
2
4 0 r
Из геометрических соображений r 2 R 2 x 2 ,cos
x
R2 x2

5.

1
dq
E
4 0 R 2 x 2
x
R x
2
2
В центре кругового витка x=0
1
qx
4 0 ( R x )
2
E 0
Однородное электрическое поле
E const
2
3
2

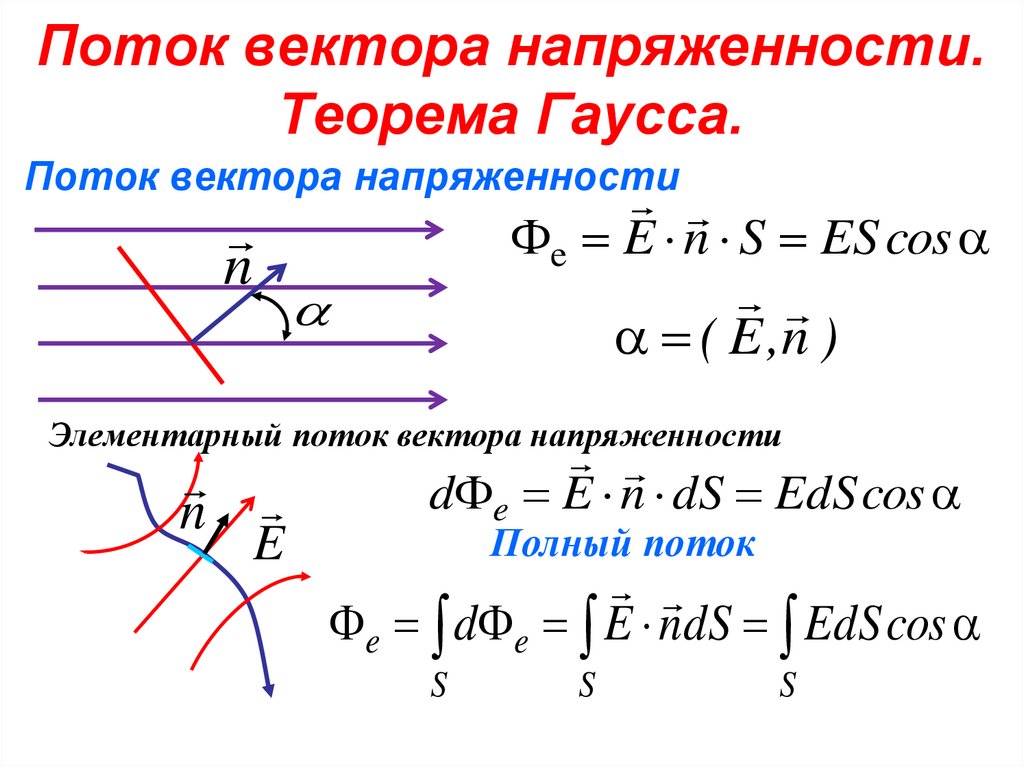
6. Поток вектора напряженности. Теорема Гаусса.

Поток вектора напряженности
n
e E n S ES cos
( E ,n )
Элементарный поток вектора напряженности
n
E
d e E n dS EdS cos
Полный поток
e d e E ndS EdS cos
S
S
S

7.

Поток вектора напряженности поля точечного заряда
q
dS
e EdS cos EdS
E
S
S
n
0
На поверхности сферы
1 q
E
const
2
4 0 r
Тогда
1 q
q
2
4 r
e E dS ES
2
4
0 r
0
S

8.

q3
q1 q2
q
e1 e 2 ...
0
Если поле создано системой зарядов
e E ndS ( E1 E2 ... En )ndS
S
S
e1 e 2 ... en
Теорема Гаусса
e E ndS
S
qi
i
0

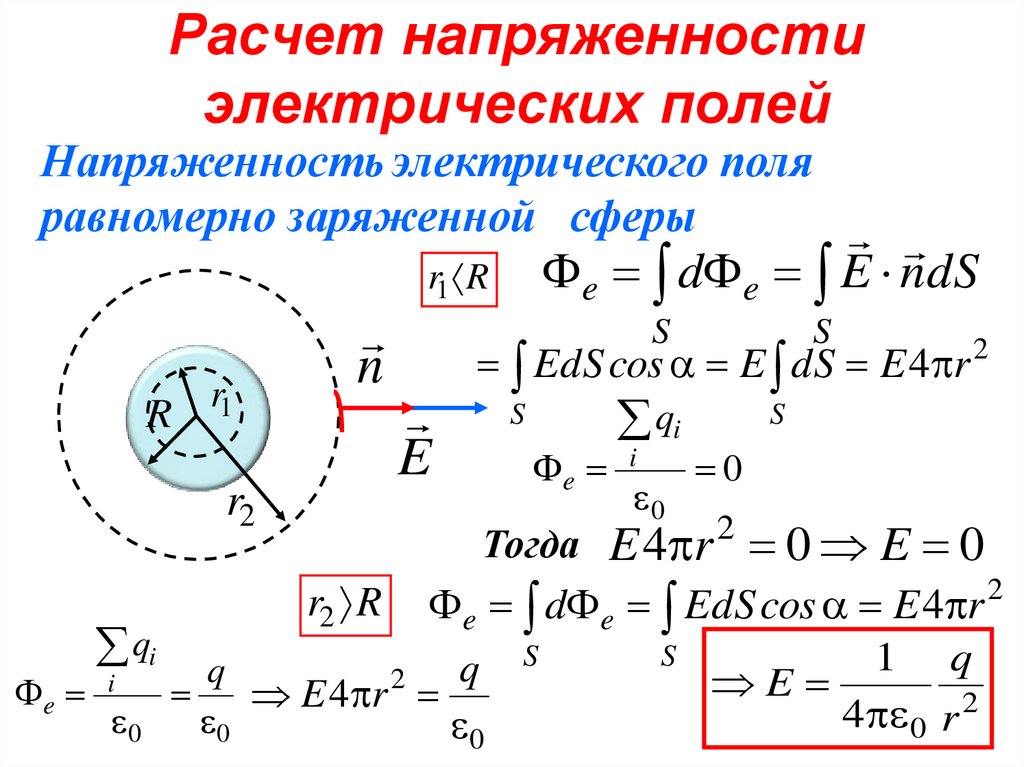
9. Расчет напряженности электрических полей

Напряженность электрического поля
равномерно заряженной сферы
e d e E ndS
r1 R
R
r1
n
r2
S
E
EdS cos E dS E 4 r 2
S
e
Тогда
r2 R
S
qi
i
0
S
0
E 4 r 0 E 0
2
e d e EdS cos E 4 r 2
qi q
S
S
1 q
q
2
E
e i
E 4 r
2
4
r
0
0
0
0

10.

Напряженность поля равномерно заряженной нити
dq q
n
d
E
n E
e d e EdS cos
S
S
EdS cos 1 2 EdS cos 2
S1
S2
E dS ES1 E 2 r
e
qi
i
0
0
s1
E
E 2 r
0
2 0r

11.

Напряженность поля равномерно заряженной
плоскости
n
dq q
dS S
E
e EdS cos
E
s
n
EdS cos 1 2 EdS cos 2
S1
e
qi
i
0
2E dS 2ES2
S2
0
S2
S2
S2
2ES2
0
E
2 0

12. Потенциальная энергия в электрическом поле.

r1
q
A12 F d
2
F d
dr
q
ds
r
q 0, q 0
1
d dr ds
2
2
2
r2 F dr F ds F dr
1
2
1
1
1
q q
4 0 r
2
dr
q q
4 0
qq
1 qq
4 0 r1 4 0 r2
1
1
1 r2
r r1

13.

Работа равна изменению потенциальной энергии
A W W1 W2
Потенциальная энергия
взаимодействия двух точечных
зарядов
Wnp
Потенциал
электрического поля
q
qq
W
4 0 r
1
W q
np
Потенциал поля
точечного заряда
Потенциал поля
системы зарядов
Работа сил
электрического поля
Разность потенциалов
Потенциал точки поля
1 q
qq 1
4 0 r q 4 0 r
1
1 2 ... n i
i
A12 q 1 q 2 q( 1 2 ) q
1 2
A1
1
q

14.

СВЯЗЬ НАПРЯЖЕННОСТИ И
ПОТЕНЦИАЛА
dA F d q E d
Работа сил электрического поля
dA qd qE d qd d E d
d ( Ex dx E y dy Ez dz )
d dx dy dz
x
y
z
Ex
,Ey
, Ez
x
y z
Полный дифференциал
В векторной форме E (
i
j k ) grad
x
y
z
2
1 2 E d
1
Для замкнутого контура
E
d
0

15.

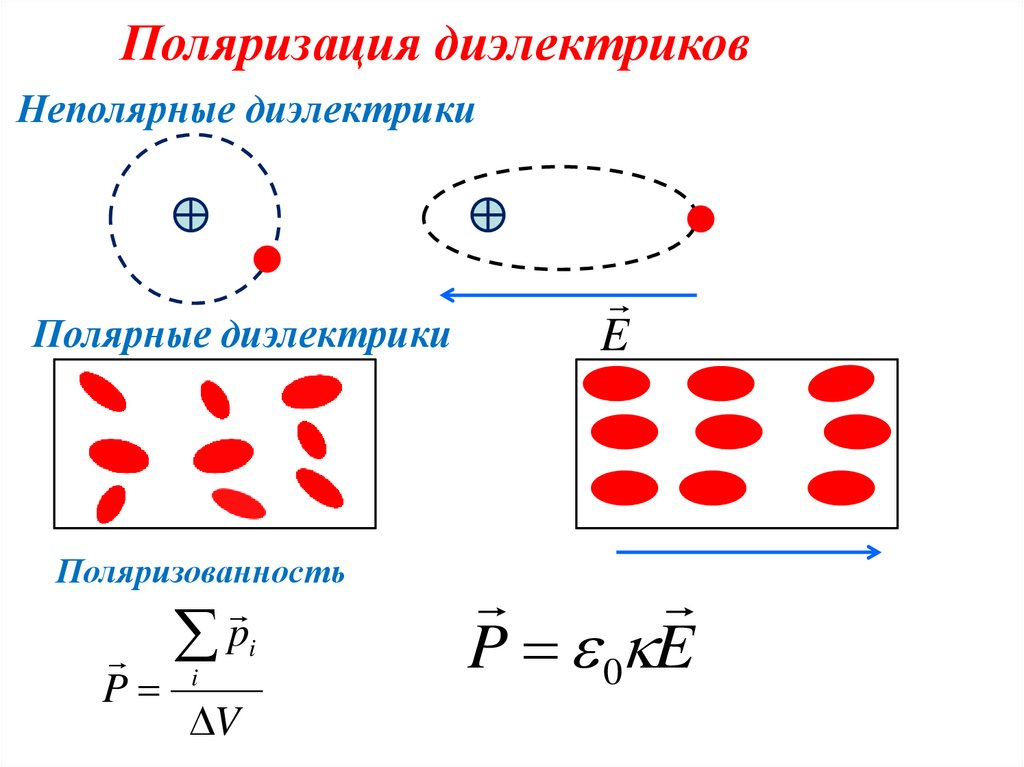
Поляризация диэлектриков
Неполярные диэлектрики
Полярные диэлектрики
Поляризованность
P
pi
i
V
E
P 0 E

16. Теорема Гаусса в диэлектриках

dV l dS cos , (E, n )
E
dS
p pi P dV P l dS cos
n
i
q ds, q ds
p q l ds l
ds l P l ds cos P cos P n
dq ds P cos ds P n ds
q dq i P n dsi P n ds
i
i
s

17. Электрическое смещение.

i q i
s E n ds 0
q i q i 0 q i
0 E n ds q i (q i 0 q i ) q i 0 q i
i
i
i
0 E n ds q i 0 P n ds
s
i
i
s
s
0 E n ds P n ds (P 0E)n ds qi0
i
D P 0 E 0 E 0 E (1 )E 0 E
s
s
s
Теорема Гаусса в диэлектрике D nds q i 0
s
i

18. Электроемкость. Конденсаторы.

Электроемкость проводника
q
C
Плоский конденсатор
E
E
E
E
E
E
Конденсатора
q
q
C
1 2 U
По принципу суперпозиции
E E E
вне
E1 E E 0
внутри
E2 E E
q d
1 2 U E d
d
0
0S
q q 0 S 0 S
Емкость конденсатора C
U
q d
d

19.

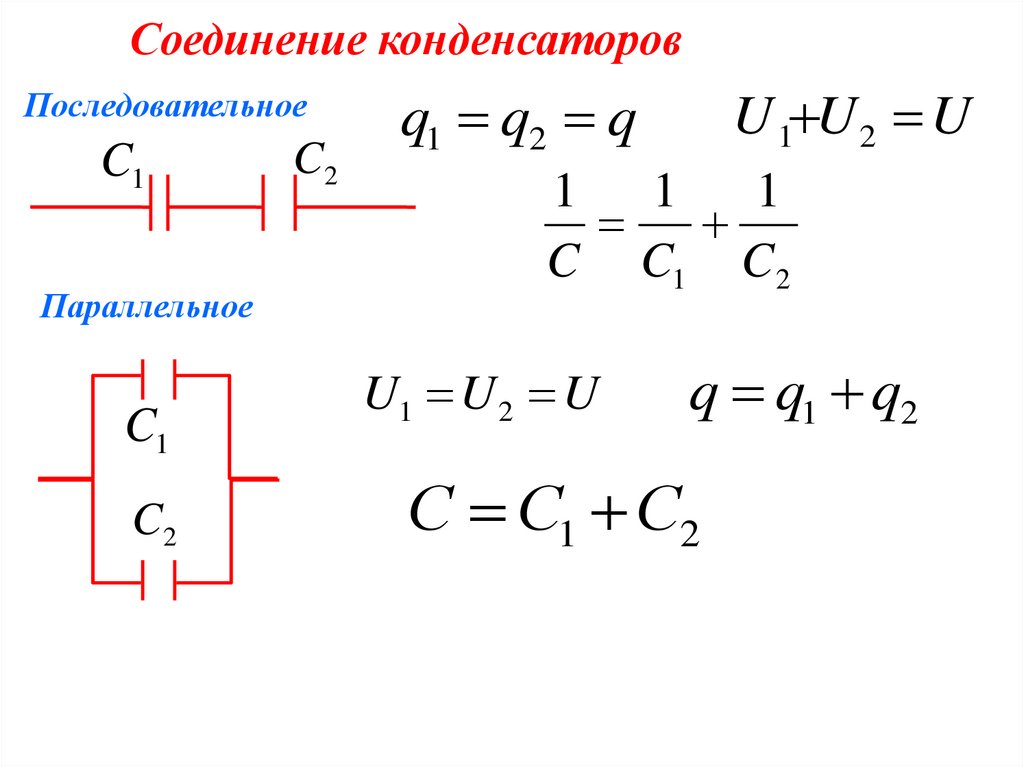
Соединение конденсаторов
Последовательное
C1
Параллельное
C1
C2
C2
q1 q2 q
U 1 U 2 U
1
1
1
C C1 C2
U1 U 2 U
q q1 q2
С С1 С2

20. Энергия электрического поля

1
W Wij
2 j i j
Энергия системы зарядов
Энергия взаимодействия двух зарядов
1 n n
W
2 i 1 j 1
qiq j
1
Wij
4 0 rij
n
qiq j
qj
1
1 n
1
qi
4 0
rij
2 i 1
rij
j 1 4 0
1 q ij
i ij
rij
j 1
j 1 4 0
n
n
n
1 n
1 n
W q i ij q i i
2 i 1 j 1
2 i 1
Энергия заряженного проводника
1
W dq i i
2 i
i const
2
2
1
q C
q
W dq i
2 i
2
2
2C

21.

Энергия заряженного конденсатора
1
1
1
1
W ( q i 1 ( q i ) 2 ) (q 1 q 2 ) q ( 1 2 ) qU
2 i
2
2
2
i
qU q 2 CU 2
W
2
2C
2
Энергия электрического поля
1 0s 2 1 0s
1
2
W
U
(Ed ) 0 E 2 (sd )
2 d
2 d
2
Объемная плотность энергии
W
dW
V
dV
0 E V 0 E
ED
D
2V
2
2
2 0
2
В однородном поле
0 2
W
E V
2
2
2
2
ED E ( P 0 E ) 0 E
EP
В диэлектрике
2
2
2
2