Треугольник

1.

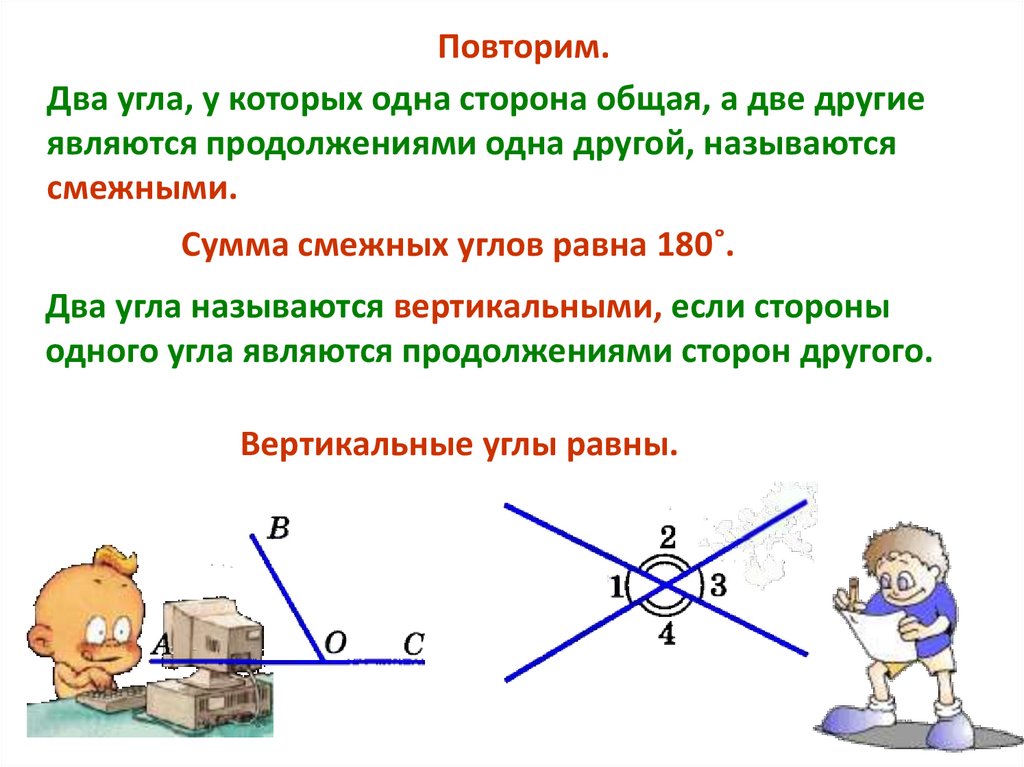
Повторим.
Два угла, у которых одна сторона общая, а две другие
являются продолжениями одна другой, называются
смежными.
Сумма смежных углов равна 180˚.
Два угла называются вертикальными, если стороны
одного угла являются продолжениями сторон другого.
Вертикальные углы равны.

2.

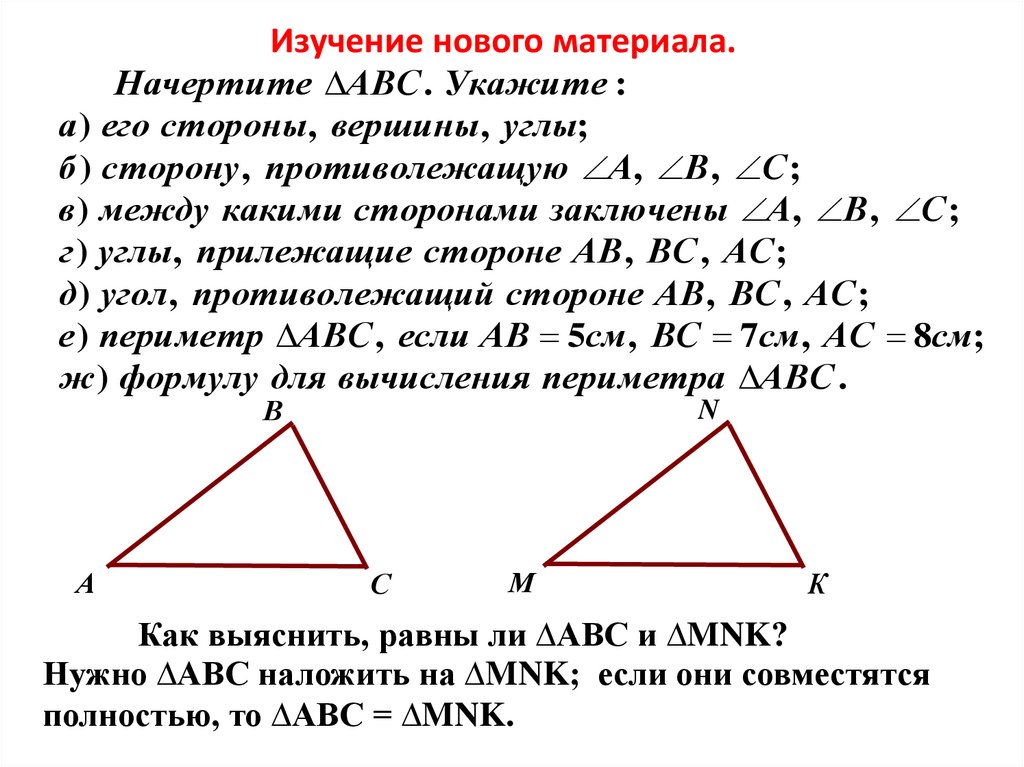
Изучение нового материала.
Начертите АВС . Укажите :
а ) его стороны, вершины, углы;
б ) сторону , противолежащую А, В , С ;
в ) между какими сторонами заключены А, В , С ;
г ) углы, прилежащие стороне АВ , ВС , АС ;
д ) угол, противолежащий стороне АВ , ВС , АС ;
е ) периметр АВС , если АВ 5см , ВС 7см , АС 8см;
ж ) формулу для вычисления периметра АВС .
В
А
N
С
М
К
Как выяснить, равны ли ∆АВС и ∆MNK?
Нужно ∆АВС наложить на ∆MNK; если они совместятся
полностью, то ∆АВС = ∆MNK.

3.

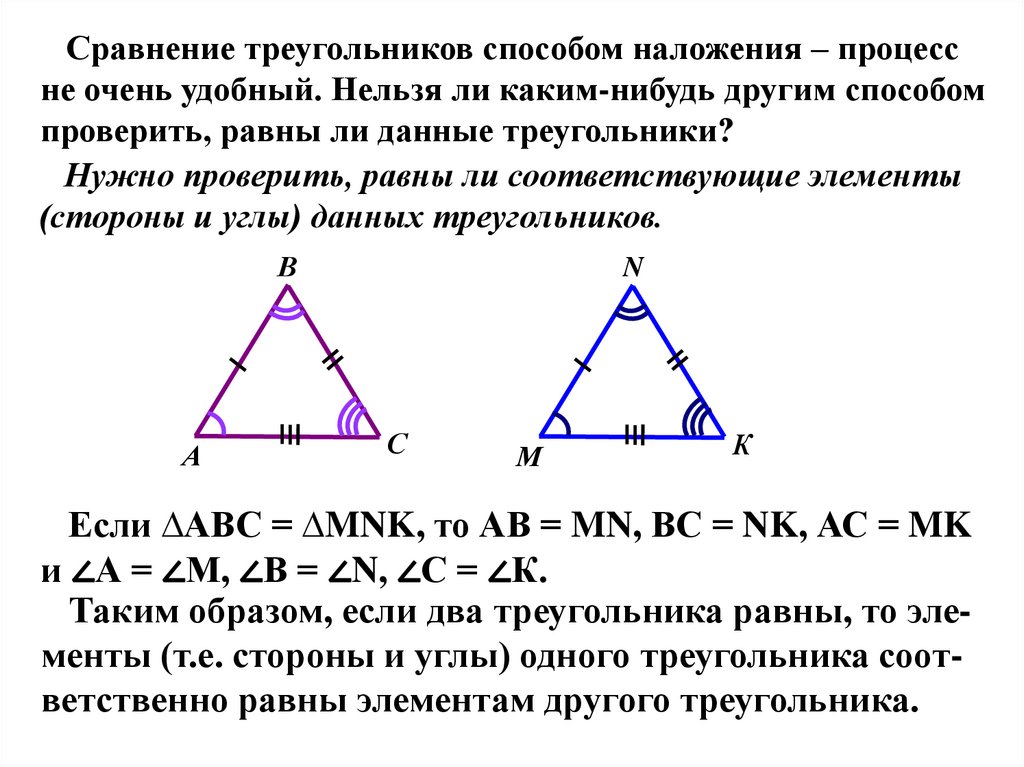
Сравнение треугольников способом наложения – процесс
не очень удобный. Нельзя ли каким-нибудь другим способом
проверить, равны ли данные треугольники?
Нужно проверить, равны ли соответствующие элементы
(стороны и углы) данных треугольников.
В
А
N
С
М
К
Если ∆АВС = ∆MNK, то АВ = MN, ВС = NK, АС = MK
и ∠А = ∠М, ∠В = ∠N, ∠С = ∠К.
Таким образом, если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.

4.

Отметим, что в равных треугольниках против
соответственно равных сторон (т.е. совмещающихся
при наложении) лежат равные углы, и обратно:
против соответственно равных углов лежат равные
стороны.
Оказывается, что равенство двух треугольников
можно установить, не накладывая один треугольник на
другой, а сравнивая только некоторые их элементы.
Как это сделать, мы обсудим на следующих уроках.
Такая возможность – установить равенство двух
фигур, не производя наложения одной на другую, а
измеряя и сравнивая лишь некоторые элементы этих
фигур, важна для практики, например для сравнения
двух земельных участков.