Похожие презентации:
Функции комплексного переменного, аналитические функции
1.
ФУНКЦИИ КОМПЛЕКСНОГОПЕРЕМЕННОГО,
АНАЛИТИЧЕСКИЕ
ФУНКЦИИ
2.
Функция кoмплексно го переменного f z : D C C ;w f z u x, y i v x, y ; u , v : R 2 R;
Примеры функций :
1) w z 2 x iy x 2 y 2 2i xy; u x 2 y 2 ; v 2 xy;
2
2) w
1 1 z
x iy
x
y
2
;
u
;
v
;
z z z x y2
x2 y2
x2 y2
3) w e z e x iy e x e iy e x cos y i sin y ; u e x cos y; v e x sin y;
w e z : C C \ {0};
| w | | e z | u 2 v 2 e 2 x cos 2 y e 2 x sin 2 y e 2 x e x ; Arg w arctg
4) w sh z ; w ch z ; w th z
sh z
ch z
; w cth z
;
ch z
sh z
v
arctg tg y y;
u
e z e z e x cos y i sin y e x cos y i sin y
e x e x
e x e x
sh z
cos y
i sin y
2
2
2
2
shx cos y i chx sin y; u shx cos y; v chx sin y;
e z e z
ch z
chx cos y i shx sin y; u chx cos y; v shx sin y;
2
Примеры :
sh 4 5i sh 4 cos 5 i ch 4 sin 5; ch 2 i ch 2 cos i sh 2 sin ch 2;
3.
Тригономет рические функции :e iz e iz
e iz e iz
w cos z
; w sin z
;
2
2i
e iz e iz e ix y e ix y e y cos x i sin x e y cos x i sin x
sin z
2i
2i
2i
e y e y i
e y e y
i sin x
sin x chy i cos x shy; u sin x chy; v cos x shy;
cos x
2i i
2i
Формулы, связывающи е гиперболич еские и тригонометрические функции :
e iz e iz
e iz e iz
ch iz
cos z; sh iz
i i sin z; cos iz chz; sin iz i shz ;
2
2i
cos z cos x iy cos x cos iy sin x sin iy cos x chy i sin x shy;
Примеры :
вычислить : cos 2 3i cos 2 ch3 i sin 2 sh3;
| cos 2 3i | cos 2 2 ch 2 3 sin 2 2 sh 2 3; arg cos 2 3i arctg tg 2 th3 ;
Функции w e z ; chz; shz явялются функциями периодическими с периодом 2 i :
e 7 2 i e 7 ; ch 1 2 i ch 1 ; sh 5 4 i sh 5 sh 5 ;
Функции cos z; sin z периодичны с периодом 2 ;
4.
W Ln z Ln | z | e i Arg z1
y
ln x 2 y 2 i arctg 2 k i, k Z ;
2
x
1
y
w ln z ln x 2 y 2 i arctg ; w ln z : C \ {0} C
2
x
z
Свойства логарифма : ln z1 z 2 ln z1 ln z 2 ; ln 1 ln z1 ln z 2 ; ln z k k ln z ;
z2
Ln z k k Ln z : Ln z k
k
y
ln x 2 y 2 ki arctg 2 ni, n Z
2
x
y
1
k Ln z k ln x 2 y 2 i arctg 2 kni; kn Z
x
2
Примеры :
1) Ln 1 3i ln 2
3
i 2 ki, k Z ; Ln 4 ln 4 i 2 ki; Ln i
2
i 2 ki, k Z
5.
2) Решить уравнение : sin z 2 z Arc sin 2 ?eiz e iz
1
2 e iz iz 4i 0 : t e iz t 2 4it 1 0 : D 16 4 12
2i
e
4i 2 3i
t1, 2
2 3 i
2
a ). e iz 2 3 i iz Ln 2 3 i ln 2 3
б ). eiz 1 3 i iz Ln 2 3 i ln 2 3
2
2
3) Вычислить : i i ?
z e
a
a Ln z
i e
i
i Ln i
e
i i 2 ki
2
e
2 k
2
, k Z.
i 2 k i, k Z
i 2 ki, k Z .
6.
С-ДИФФЕРЕНЦИРУЕМОСТЬ7.
ПРИМЕРЫ С-ДИФФ. И НЕ ДИФФ. ФУНКЦИЙ1)f(z)=2x-3iy; u(x,y)=2x; v(x,y)=-3y;
z0 a ib C : f ' z0 lim
z 0
f ( z0 z ) f z0
2 x 3i y
lim
x 0 x i y
z
y 0
3i y
lim
x 0 i y 3
y 0
пределы различны, значит предела не существует
2 x
lim
2
x 0 x
y 0
нет производной ни в одной точке С f z не явлется С дифференци руемой.
2) f(z)=|z|2=x2+y2;
a 2 b 2 2a x 2b y x 2 y 2 a 2 b 2
z0 a ib : f ' z0 lim
x 0
x i y
y 0
2b y y 2
2b y
lim
2ib
lim
x 0
y 0
i
y
i
y 0
пределы различны, если только a b 0
2
2
a
x
x
lim
lim 2a x 2a
x 0
x 0
x
y 0
при a b 0 пределы равны. f z C дифференци руема в точке z 0; f ' 0 0.
8.
9.
ПРИМЕНЕНИЕ УСЛОВИЙ КОШИ -РИМАНА1) f z 2 x 3iy : u 2 x; v 3 y R 2 дифференцируемы;
u ' x 2 v' y 3
Условия Коши Римана :
не является С дифф. ни в одной точке С
u
'
v
'
0
y
x
2) f z | z |2 : u x 2 y 2 ; v 0 R 2 дтфференцируемые;
u ' x 2 x v' y 0 2 x 0 x 0
условия Коши Римана :
f z С дифф. в т. z 0
u
'
2
y
v
'
0
2
y
0
y
0
x
y
f ' 0 ?
Формулы для вычисления поизводной :
f
u i v
lim
y 0, т.к. предел существует
x 0 x i y
z 0 z
f ' z0 ? f ' z0 lim
y 0
u i v
u
v
lim
i lim
u ' x x0 ; y0 iv ' x x0 ; y0 условия Коши Римана
x 0
x 0 x
x 0 x
x
v' y x0 ; y0 iv ' x x0 ; y0 v' y x0 ; y0 i u ' y x0 ; y0 u ' x x0 ; y0 i u ' y x0 ; y0 ;
lim
f ' 0 v' y iv ' x | 0;0 0 i 0 0
10.
3) f z y 2 2ix 2 ; u y 2 ; v 2 x 2 R 2 дифференцируемы;Условия Коши Римана :
u ' x 0 v' y 0 u ' x v' y x, y
Функция f z С дифф. на {z : y 2 x}
u ' y 2 y; v ' x 4 x 4 x 2 y 4 x y 2 x
z0 1 2i {z : y 2 x} f ' 1 2i u ' x i v' x
z z0
0 i 4 x x 1 4i;
y 2
11.
ПРИМЕРЫ ФУНКЦИЙ:4) f(z)=ez;
u x; y e x cos y; v x; y e x sin y; R 2 дифференци руемые
Условия Коши Римана :
u ' x v' y e x cos y
x; y C f z С дифференци руема z С
x
u ' y v' x e sin y
f ' z u ' x i v' x e x cos y i e x sin y e z
Теорема.
Все элементарные функции комплексного переменного имеют те же
производные, что и для функций действительного переменного.
1
cos z ' sin z; ln z ' ; z n ' nz n 1;.....
z
12.
ГОЛОМОРФНЫЕ ИЛИ АНАЛИТИЧЕСКИЕФУНКЦИИ
13.
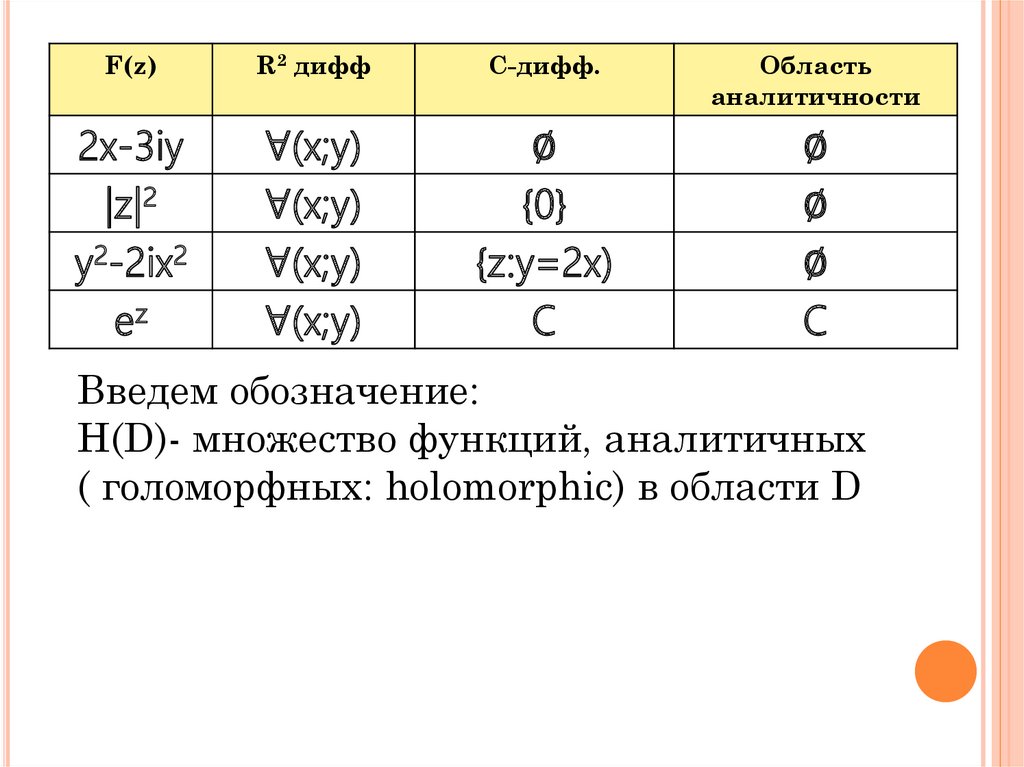
F(z)R2 дифф
С-дифф.
Область
аналитичности
2x-3iy
|z|2
y2-2ix2
ez
∀(x;y)
∀(x;y)
∀(x;y)
∀(x;y)
∅
{0}
{z:y=2x)
C
∅
∅
∅
C
Введем обозначение:
H(D)- множество функций, аналитичных
( голоморфных: holomorphic) в области D
14.
СВОЙСТВА АНАЛИТИЧЕСКИХ(ГОЛОМОРФНЫХ)ФУНКЦИЙ
u ' x v' y
f ( z ) H ( D) f ( z ) дифференцируема в D
в D
u ' y v' x
u ' x u ' y v' ' xy v' ' yx 0 в D;
x
y
v v' ' xx v' ' yy u ' ' xy u ' ' yx 0 в D.
u u ' ' xx u ' ' yy
15.
Пример : w ln z;y
u ( x, y ) 0,5 ln( x y ); v( x, y ) arctg ;
x
u 0 ?
2
2
x
y
u'x 2
; u' y 2
;
2
2
x y
x y
u ' ' xx
y x
2
x
2
y
2
2 2
; u ' ' yy
x y
2
x
2
y
2
2 2
u 0
16.
ПРИМЕРЫ1) Существуют ли гармонические функции вида u ( x, y ) ( xy) ?
t xy u ' x 't t ' x ' y; u ' y ' x;
u ' ' xx ' ' y 2 ; u ' ' yy ' ' x 2 u ' ' y 2 ' ' x 2 ' ' y 2 x 2 0
' ' 0 (t ) C1t C2 C1 xy C2
u ( x, y ) C1 xy C2 ;
2) Являются ли функции u ( x, y ) x 3 3 xy2 4 v( x, y ) 3x 2 y y 3 7
сопряжённо й парой гармонических функций ?
u ' x v' y
Решение : проверим условия Коши Римана для этих функций :
u ' y v' x
u ' x 3 x 2 3 y 3 ; v' y 3 x 2 3 y 2 u ' x v' y x, y;
u ' y 6 xy; v' x 6 xy u ' y v' x x, y;
Таким образом u ( x, y ) v( x, y ) сопряжённа я пара гармонических функций .
f ( z ) u iv z 3 4 7i
17.
СВОЙСТВА АНАЛИТИЧЕСКИХ ФУНКЦИЙЕсли u 0 в D
v 0 в D , то cоопряженная ей функция v x, y :
u , v являются сопряженно й парой гармонических функций и удовлетворяют
в области D условиям Коши Римана :
u ' x v' y
u 0 в D v :
в D; f z u iv;
u ' y v' x
18.
Пусть u ( x, y ) гармоническая функция в D :u 0 ( x, y ) D v( x, y ) : u , v сопряженна я пара
гармонических функций и f ( z ) u iv.
u ' x v' y v( x, y ) u ' x dy C , причем C C ( x) :
u ' y v' x u ' y u ' x dy C ' x u ' ' xx dy C ' x
x
u ' ' yy u ' ' xx dy C ' x u ' ' xx C ' x
y
y
y
C ' x u ' ' xx u ' ' yy u 0 C C ( x).
y
v( x, y ) u ' x dy C ( x).
19.
1)Восстановить функцию по её известной действительной
части:
u ( x, y ) x 2 y 2 y ln( x 2 y 2 )
v ( x, y ) ? f ( z ) ?
1)v( x, y ) ?
u ' x v' y
2x
2y
y2 x2
x2 y2
u 2 x 2
2
y
1
2
2
0
v
x
,
y
:
2
2
x y 2 x
x 2 y 2 y
x2 y2
x2 y2
u ' y v' x
'
'
1
dy
2x
2x
x
dy C x 2 xy 2
u ' x v ' y v ' y x, y 2 x 2
v x, y 2 x 2
C x ;
2
2
x y2
x
y
y
1
x
y
v x, y 2 xy 2arctg C x ;
x
2y
1
2y
2y
y
u ' y v ' x : 2 y 1 2
2 y 2
2 C ' x 1 2
2
C ' x
2
2
2
2
x y
x
x
y
x
y
y
1
x
y
C ' x 1 C x x c v x, y 2 xy 2arctg x c;
x
2) f z u iv ?
y
f z x 2 y 2 y ln x 2 y 2 i 2 xy 2arctg x c
x
y
x 2 y 2 2ixy 2 ln x 2 y 2 i arctg ix y ci z 2 2 ln z i x iy ci z 2 iz 2 ln z ci;
x
20.
2) Восстановить функцию f(z) по известноймнимой части и условию f(-i)=2i;
v( x, y ) 2 xy y 2 x 2 chx cos( y 1)
1)u ( x, y ) ? v 0;
u ' x v' y 2 x 2 y chx sin y 1 u 2 x 2 y chx sin y 1 dx
x 2 2 xy shx sin y 1 C y
u ' y v' x 2 y 2 x shx cos y 1 ; u ' y 2 x shx cos y 1 C ' y
2 x shx cos y 1 C ' y 2 y 2 x shx cos y 1 C ' y 2 y
C y y2 c
u x, y x 2 2 xy y 2 shx sin y 1 c
2) f z ?
f z u iv x 2 y 2 2 xy shx sin y 1 c i 2 xy y 2 x 2 chx cos y 1
x 2 y 2 2ixy 2 xy i y 2 x 2 shx sin y 1 ichx cos y 1 c
z 2 i x 2 y 2 2ixy i chx cos y 1 ishx sin y 1 c
z 2 iz 2 i cos ix cos y 1 sin ix sin y 1 c 1 i z 2 i cos ix y 1 c
1 i z 2 i cos i x i y 1 c 1 i z 2 i cos i z i c cos it cht
1 i z 2 i ch z i c f i 1 i i ch i i c 1 i i c 2i c 1
f z 1 i z 2 i ch z i 1
21.
3) Можно ли восстановить функцию f(z)∊H(C),если
3.1.
u (x2 y 2 )
3.2. v (xy)
Ответ: да, если эти функции гармонические:



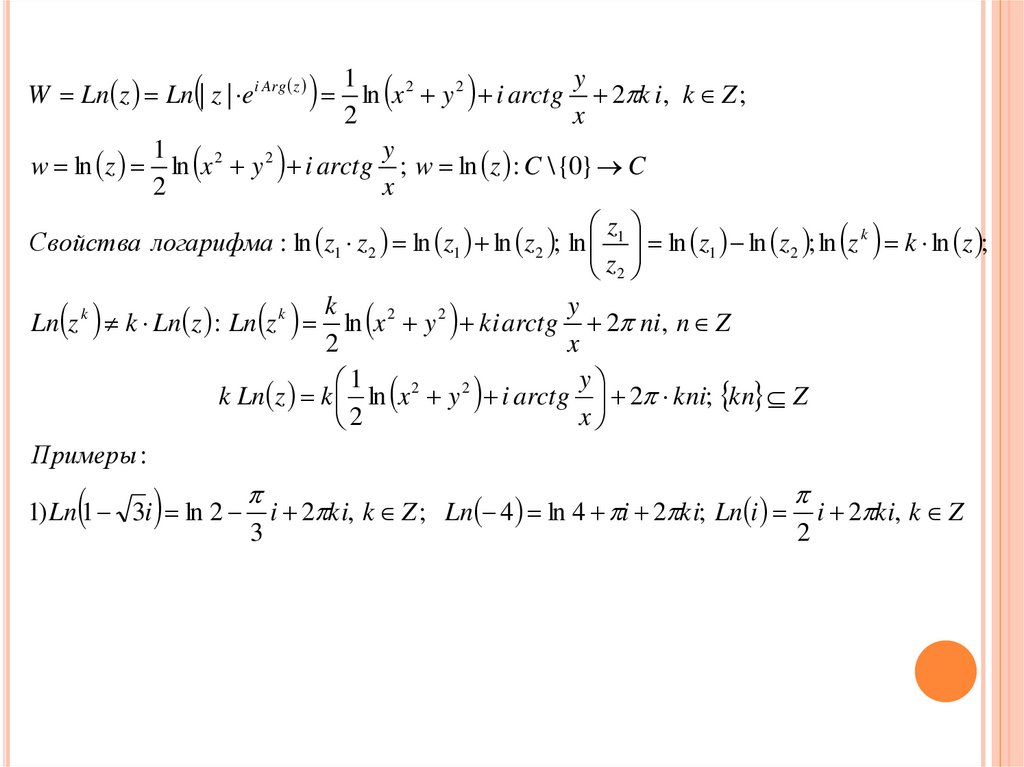









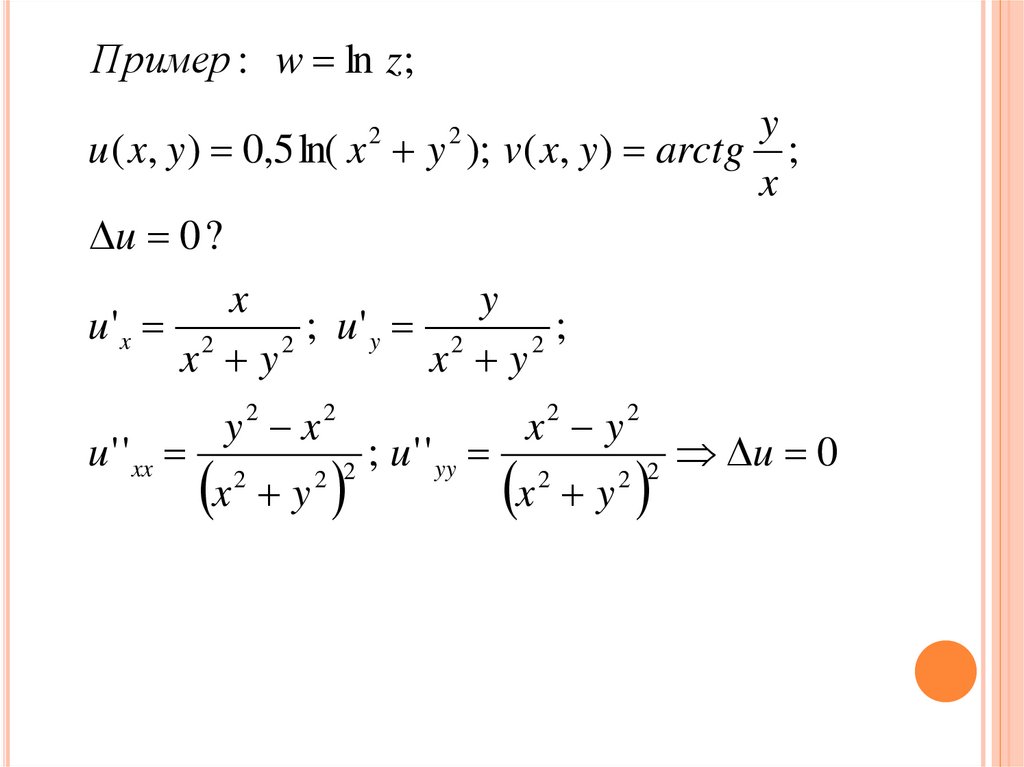






















 Математика
Математика








