Похожие презентации:
Гидроудар. Изэнтропические соотношения в сжимаемых средах. Уравнение баланса. Число Маха и скоростной коэффициент
1.
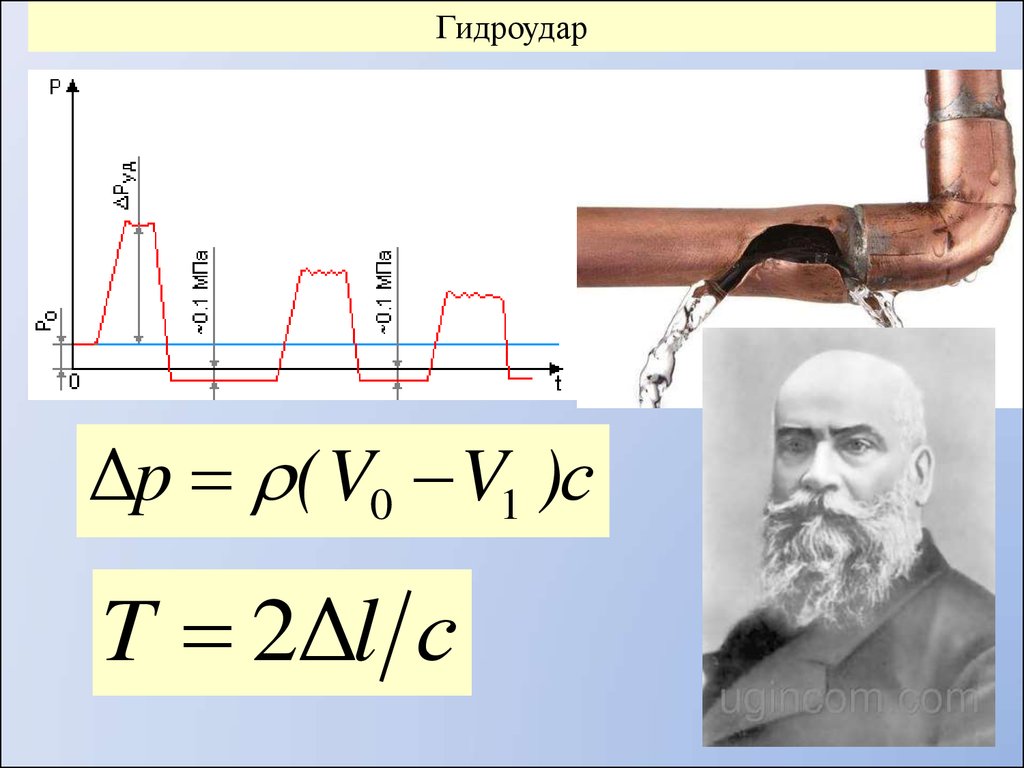
ГидроударΔppΩ t (Ω
Δ
Vl0( V 0V 1V)1с)
Δl 2 cT 2
T 2Δl с
2.
Изэнтропические соотношения в сжимаемых средах.Уравнение баланса энергии в сжимаемых средах.
Число Маха и скоростной коэффициент.
Изэнтропические соотношения.
Одномерное стационарное движение сжимаемой среды по трубе
переменного сечения
3.
Уравнение баланса энергии.•При стационарном (баротропном) движении идеальной среды
под действием потенциальных объемных сил сумма кинетической
энергии единицы массы, внутренней энергии и потенциала
объемных сил сохраняет вдоль линии тока постоянное значение.
2
d V
( П U) 0
dt 2
dh dU RdT
•Энтальпия — это та энергия,
которая доступна для
преобразования в теплоту при
определенном постоянном
давлении
h C T
p
dp d V 2
dU dh
(
h
)
0
( p) dt 2
4.
Число Маха.Если в потоке истечения скорость сжимаемой среды достигнет в
выходном сечении патрубка местной скорости звука, называемой
критической, то в этом, также называемом критическим
сечении, давление, температура и плотность примут одинаковые
для всех частиц среды значения тоже называемые критическими.
В адиабатическом движении сжимаемой среды критические
значения параметров состояния определяются по статическим
значениям параметров.
5.
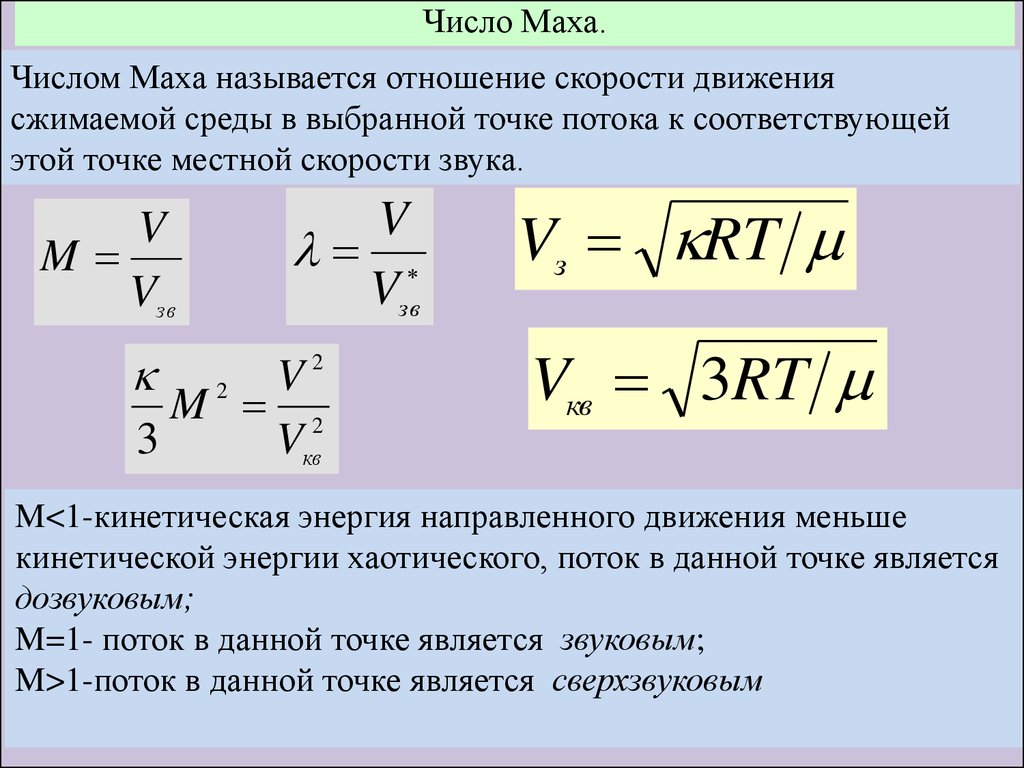
Число Маха.Числом Маха называется отношение скорости движения
сжимаемой среды в выбранной точке потока к соответствующей
этой точке местной скорости звука.
V
Vзв
V
M
Vзв
2
V
M 2
3
Vкв
2
Vз RT
Vкв 3RT
M<1-кинетическая энергия направленного движения меньше
кинетической энергии хаотического, поток в данной точке является
дозвуковым;
M=1- поток в данной точке является звуковым;
M>1-поток в данной точке является сверхзвуковым
6.
Изэнтропические формулы2
V
С
h p Th 0 C pT0
2
T
1 2 1
(1
M )
T0
2
T 1 1 1 2 1 1
(1 )
M )
00 T0 2
p
T 1
(1 )
M )
p0 T0 2
1
2
1
h C pT
h0 C pT0
Vзв2
h
( 1)
V Vзв Vзв
1 2
V
h h0 h0 2( 1) Vзв
2
2
1
2
M
1 2
1
M
2
7.
Одномерное стационарное движение сжимаемой среды по трубепеременного сечения
•Не учитывая кривизну оси канала, выбираем в качестве оси ось
координаты x.
•Поток сжимаемой среды считаем адиабатическим, саму среду
идеальной, поэтому движение среды можно считать
изэнтропическим
dV
Vdx
dp
dp
2 d
Vx Vзв
V x dVx
dt
x
dx
d
2
2 dVx dΩ 2 dΩ
d
dV
(Vx Vзв ) x V
зв 0
Ω
Vx Vx Ω
dVx 1 dp
dΩ
dV
2x
( M V1x)
Vx dx
Ω
dx
VxΩ const
8.
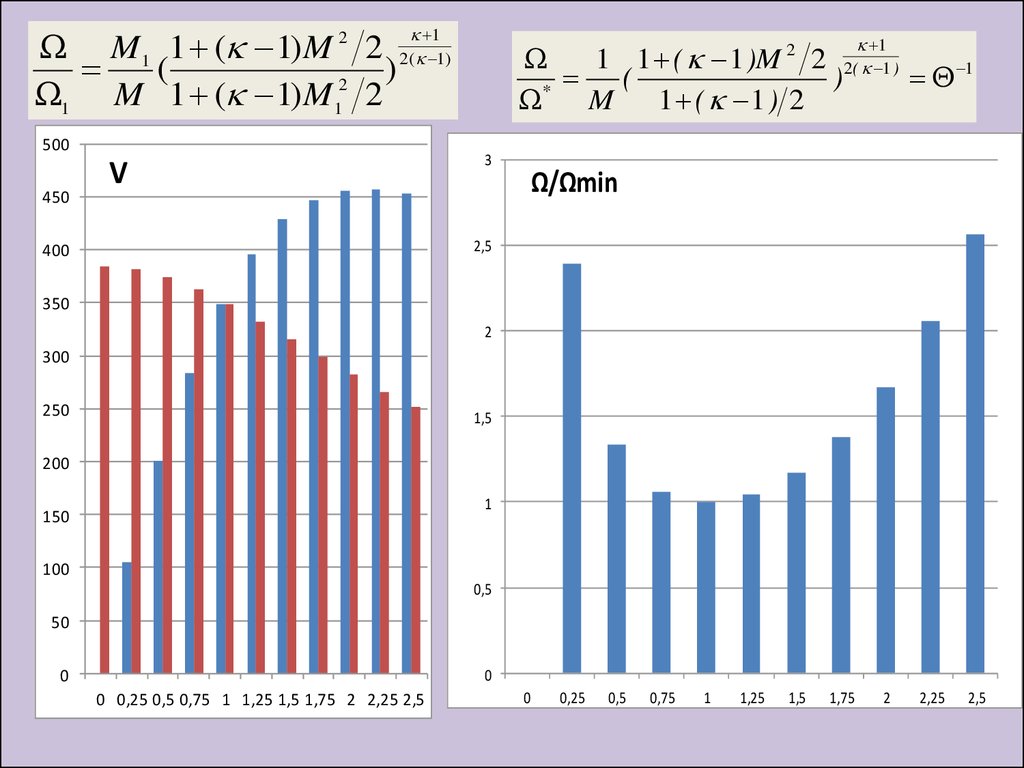
Ω M1 1 ( 1) M 2 2 2 ( 1)(
)
2
Ω1 M 1 ( 1) M1 2
1
500
450
V
Ω
1 1 ( 1 )M 2
(
)
*
Ω
M
1 ( 1 ) 2
2
3
1
2( 1 )
Θ 1
Ω/Ωmin
2,5
400
350
2
300
250
1,5
200
1
150
100
0,5
50
0
0
0 0,25 0,5 0,75 1 1,25 1,5 1,75 2 2,25 2,5
0
0,25
0,5
0,75
1
1,25
1,5
1,75
2
2,25
2,5






 Физика
Физика








