Обработка экспериментальных данных. Многофакторная регрессия. Лекция 7

1.

Обработка экспериментальных данных
Лекция 7:
Многофакторная регрессия
Преподаватель: Аникеева Александра Евгеньевна

2.

Отбор факторных признаков для включения в модель
Находят коэффициенты парной корреляции rX1X 2 , rX1X 3 , rX 2 X 3 .
Если их значения меньше 0,8, их включают в модель.
Пусть , rX 2 X 3 0,9 . Следовательно один из признаков -Х2 или Х3 – нужно
исключить из модели
Рассчитать коэффициенты парной корреляции между каждым из
факторов (в нашем примере Х2 и Х3)и результативным признаком Y: rYX 2 и rYX3 .
Если, получилось, что rYX 2 rYX3 , то исключают признак Х3
Если
rX i X j 1
3(1 rX2i X j )
n 1
, то один из факторов можно исключить.
Если tнабл>tкрит, (α ; n-2) то с вероятностью
1-α можно утверждать о значимости
С помощью t-критерия Стьюдента: межфакторного
коэффициента
корреляции
и,
следовательно,
о
rYX2 j
значимости факторного признака Xj. Он
t набл
( n 2)
2
1 rYX j
включается в модель.

3.

Двухфакторная регрессионная модель
y m a1 x1 a 2 x 2 b
n
n
n
a1 x1i a 2 x 2i nb yi
i 1
n
i 1
1 n
y yi ;
n i 1
i 1
n
n
n
a1 x 1i a 2 x1i x 2i b x1i yi x1i
2
i 1
i 1
n
n
i 1
i 1
a1 x1i x 2i a 2
a1
rYX1 rX1 X 2 rYX 2
1 r
2
X1 X 2
x 22i
Sy
S X1
i 1
i 1
n
n
i 1
i 1
S y2 y 2 y
,
a2
b y a1 x1 a2 x2
1 r
2
X1 X 2
2
b x 2i y i x 2i
rYX 2 rX1 X 2 rYX1
1 n 2
y yi ;
n i 1
2
2
S x2i xi2 xi , i 1,2
Sy
S X2
1 n
x j x ji ; j 1,2
n i 1

4.

Множественной линейной корреляционной связи
RY / X1 X 2
2
2
rYX
r
YX 2 2rYX1 rYX 2 rX1 X 2
1
1 rX21 X 2
Свойства множественного коэффициента корреляции:
1) 0≤R≤1
2) Если R=0, то линейная корреляционная связь между Х1 и Х2иY
отсутствует, хотя между ними может существовать нелинейная или
функциональная зависимость.
3) Если R=1, то, междуХ1 и Х2и Y существует линейная функциональная
зависимость.4) При небольшом объеме выборки величину множественного
коэффициента корректируют
^
R Y / X1 X 2
1 (1 RY2 / X1 X 2 )
n 1
n k 1
Здесь k =2 – число факторных признаков.
Для
коэффициента
множественной
корреляции
определяют
среднеквадратическую ошибку
1
R
SR
3 , то с вероятностью 0,99 можно считать R значимым.
Если
S
n 1
R

5.

Проверка адекватности модели множественной
линейной корреляции
Вычисляют статистику
Fнабл
(n k 1) ( RY / X1 X 3 ) 2
k 1 ( RY / X1 X 3 ) 2
Здесь n– объем выборки, k – число
факторных признаков
При заданном уровне значимости α и степенях свободы ν1=k и ν2=n-k-1 по
таблице критических точек распределения Фишера находят критическое
значение Fкрит. Если Fнабл >Fкрит, то уравнение регрессии согласуется с опытными
данными.
Адекватность модели множественной корреляции можно определить по
средней ошибке аппроксимации
1 n yi yim
100%
n i 1
yi
Коэффициент эластичности:
x
К э f ( x)
y

6.

1
2
3
4
5
6
7
8
9
10
4999
6929
6902
10097
8097
11116
4880
7355
10066
7884
5349
6882
7046
7248
5256
14090
3525
5431
7680
8226
420
553
570
883
433
839
933
526
676
684
Среднесписочная
численность
рабочих, чел.
Среднесписочная
численность
промышленно–
производственного
персонала, чел.
тыс. руб.
Валовая
продукция
в оптовых ценах
предприятия,
Стоимость
промышленнопроизводственных
основных фондов,
тыс. руб
№ предприятия
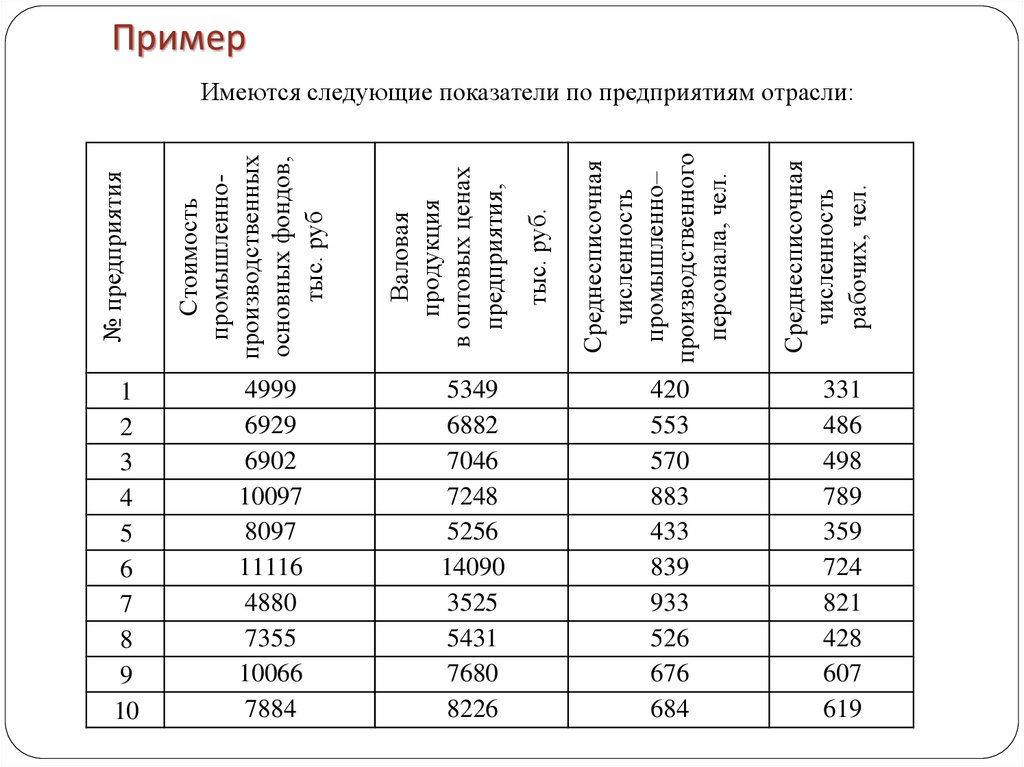
Пример
Имеются следующие показатели по предприятиям отрасли:
331
486
498
789
359
724
821
428
607
619

7.

1 10
78325
1 10 2 653107157
2
y yi
7832,5; y yi
65310715,7
10 i 1
10
10 i 1
10
2
S y y 65310715,7 7832,52 3962659,45
2
y
2
S y 3962659,45 1990,642974
2
1 10
70733
S x21 x12 x1 57287784,3 7073,32 7256211,41
x1 x1i
7073,3;
10 i 1
10
1 10 2 572877843
2
S x1 7256211,41 2693,735587
x1 x 1i
57287784,3
10 i 1
10
1 10
6517
x 2 x2 i
651,7;
10 i 1
10
1 10 2 4550205
x x 2i
455020,5
10 i 1
10
2
2
1 10
5662
566,2;
x 3i
10 i 1
10
1 10 2 3478174
2
x3 x 3 i
347817,4
10 i 1
10
x3
2
S x22 x22 x2
455020,5 651,7 2 30307,61
S x2 30307,61 174,09081
S x23 x32 x3
2
347817,4 566,2 2 27234,96
S x3 27234,96 165,030179

8.

1 10
594729518
yx1 yi x1i
59472951,8
10 i 1
10
1 10
52232475
yx 2 yi x2i
5223247,5
10 i 1
10
1 10
45525377
yx3 yi x3i
4552537,7
10 i 1
10
1 10
47529683
x1 x2 x1i x2i
4752968,3
10 i 1
10
1 10
41402962
x1 x3 x1i x3i
4140296,2
10 i 1
10
1 10
3976057
x2 x3 x2i x3i
397605,7
10 i 1
10

9.

rYX1
yx1 y x1 59472951,8 7832,5 7073,3
0,759255
S y S x1
1990,642974 2693,735587
rYX 2
yx2 y x2 5223247,5 7832,5 651,7
0,342826
S y S x2
1990,642974 174,09081
rYX3
yx3 y x3 4552537,7 7832,5 566,2
0,35851
S y S x3
1990,642974 165,030179
rX1 X 2
x1 x2 x1 x2 4752968,3 7073,3 651,7
0,30557
S x1 S x2
2693,735587 174,09081
rX1 X 3
x1 x3 x1 x3 4140296,2 7073,3 566,2
0,304565
S x1 S x3
2693,735587 165,030179
rX 2 X 3
2
rYX
0,759255 0,576469
1
2
rYX2 2 0,342826 0,11753
2
rYX2 3 0,35851 0,128529
2
rX21X 2 0,30557 0,093373
2
rX21X 3 0,304565 0,09276
2
x2 x3 x2 x3 397605,7 651,7 566,2
0,995925 rX2 X 0,995925 2 0,991866
2 3
S x2 S x3
174,09081 165,030179

10.

X 3: t набл
X 2: t набл
X 1: t набл
rYX2
3
2
1 rYX
3
rYX2
2
2
1 rYX
2
rYX2
1
2
1 rYX
1
(n 2)
0,128529 8
1,0862239
1 0,128529
(n 2)
0,11753 8
1,0322114
1 0,11753
(n 2)
0,576469 8
3,2998198
1 0,576469
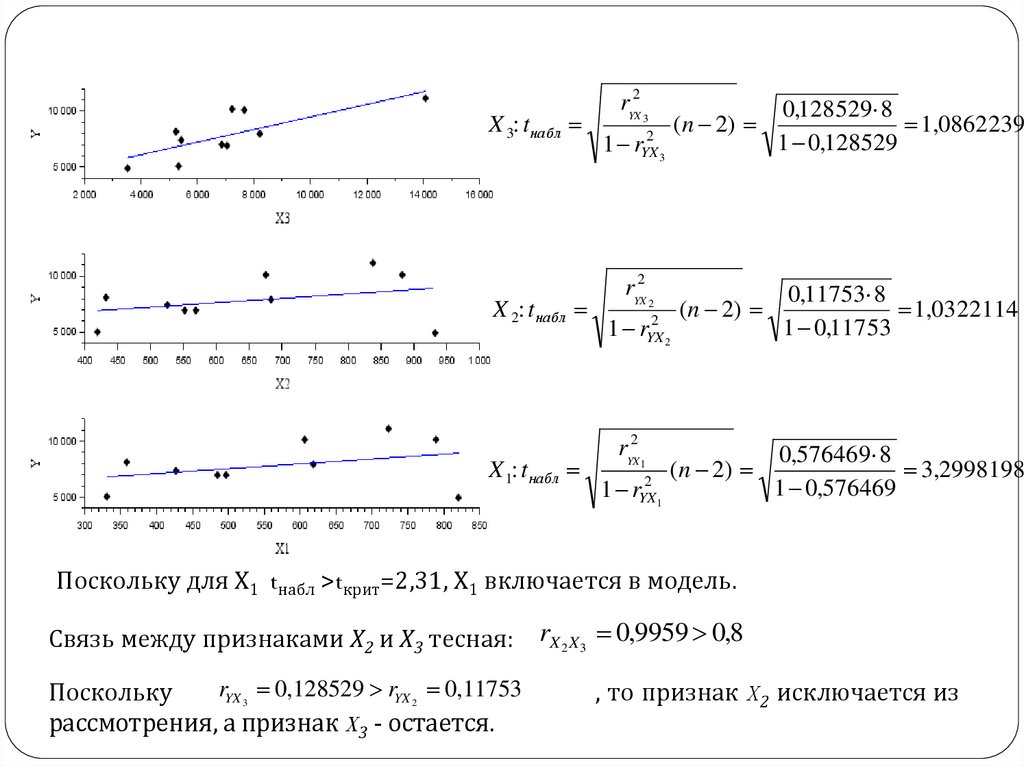
Поскольку для Х1 tнабл >tкрит=2,31, Х1 включается в модель.
Связь между признаками Х2 и Х3 тесная:
rYX 0,128529 rYX 0,11753
Поскольку
рассмотрения, а признак X3 - остается.
3
2
rX 2 X 3 0,9959 0,8
, то признак X2 исключается из

11.

Множественный коэффициент корреляции
RY / X1 X 3
2
2
rYX
r
2rYX1 rYX 3 rX1 X 3
YX
1
3
1
rX21 X 3
0,576469 0,128529 2 0,759255 0,35851 0,304565
0,7709
1 0,09276
^
RY / X X
1
2
1 (1 R 2 Y / X1 X 2 )
n 1
9
1 (1 0,77092 ) 0,69167
n k 1
7
Проверим значимость коэффициента корреляции по критерию Стьюдента
^
t выб
R
3 0,69167 2,07502
SR
По таблице критических точек распределения Стьюдента при уровне
значимости α=0,05 и числе степеней свободы k=n-3=7 находим
. tкрит 1,89458
Так как tвыб>tкрит, делаем вывод, что значим.

12.

Нахождение коэффициентов выбранной
зависимости
70733a 1 5662a 2 10 b 78325
572877843a 1 41402962a 2 70733b 594729518
41402962a 1 3478174a 2 5662 b 45525377
y 0,5295093x1 1,6922088x3 3129,061528
Общий индекс детерминации равен
R RY2 / X1 X 3 0,77092 0,59432172
Следовательно, факторные признаки, отобранные в модель, влияют на
результативный в пределах 59,43%. Это не очень сильное влияние. Согласно
закону Парето степень влияния должна быть не меньше 80%.

13.

Проверка адекватности модели
Fнабл
(n k 1) ( RY / X1 X 3 ) 2
k 1 ( RY / X1 X 3 ) 2
(10 2 1) 0,77092
5,127526
2
2(1 0,7709 )
Так как Fкрит<Fнабл ,то с вероятностью 0,95 гипотеза о статистической значимости
эмпирических данных принимается, корреляционная модель может быть построена.
Значение средней ошибки аппроксимации:
1 n yi yim
1,6110057
100%
100% 16,11%
n i 1
yi
10
Это говорит о не очень высокой точности модели.
Величины средних коэффициентов эластичности:
К э1 a1
x
x1 7073,3
566,2
0,5295093 0,47 ___ К э2 a2 3
1,69208826 0,12
y 7832,5
y 7832,5
Изменение признака Х1на 1% влечет за собой изменения признака Y на 47, 82%, а
вследствие изменения признака Х3 – на 12,23%.