Похожие презентации:
Наибольшее и наименьшее значения функции. Решение прикладных задач на оптимизацию
1. Наибольшее и наименьшее значения функции Решение прикладных задач на оптимизацию
2.
Определяя точки минимума функции,ученик нашел, при каких значениях
аргумента значения функции равны
нулю. Затем из этих значений он
выбрал те, проходя через которые
функция меняет знак с минуса на
плюс. Эти точки он назвал точками
минимума.
Прав ли он?
3.
Определяя точки минимумафункции, ученик нашел те
значения аргумента, при которых
производная обращается в нуль.
Эти точки он назвал точками
минимума.
Прав ли он?
4. График производной.
Определяя точкиминимума, ученик
указал точку х = 2.
Прав ли он?
5. График производной.
Определяя точкиминимума, ученик
указал точки:
х = -4, х = 1, х = 3.
Прав ли он?
6.
На промежутке (0;2) у`(x) > 0,на промежутке (2;3)
у`(x) < 0.
Является ли точка х = 2 точкой
максимума?
7.
Является ли точка х = 2критической для функции у(х),
если D(y) = [-3;2]?
8.
На отрезке [a;b] функция имеетмаксимум, равный 5 и минимум,
равный 2, причем у(а) = -3,
у(b) = 6.
Верно ли, что наибольшее
значение функции равно 5, а
наименьшее – равно 2?
9.
Непрерывная на отрезке [a;b]функция f(х) имеет единственную
точку максимума х=2,
причём f(2)=7.
Верно ли, что наибольшее
значение функции на отрезке
[a;b] равно 7?
10. График непрерывной функции
Область определения функции;Множество значений функции;
При каких значениях x
f (x) > 0, f (x) < 0, f(x) = 0;
При каких значениях x
f` (x) > 0, f` (x) < 0;
Чему равно наибольшее и наименьшее значение
функции?
11. Алгоритм нахождения наибольшего и наименьшего значений функции.
Найти производную функции икритические точки, лежащие
внутри отрезка [a;b]
Вычислить значения функции в
отобранных критических точках и
на концах отрезка
Выбрать наибольшее и
наименьшее значение функции
12. Проверка домашнего задания
Найти наибольшее значениефункции V(x) = (12 – x) • х2 / 2
на отрезке [0;12].
При каком х достигается это
значение?
13. Решение задачи
V(x) = (12 – x) • х2 / 2 = 6х2-0,5 хV`(x) =12x - 1,5х2, 12x - 1,5х2 = 0,
1,5х•(8 –х)=0,
х=0 , х=8.
V(0)=0
V(8) =128
V(12)=0
Наибольшее значение функции
равно 128. Это значение функция
принимает при х=8
14.
Л.Н. Толстой«Много ли человеку земли надо?»
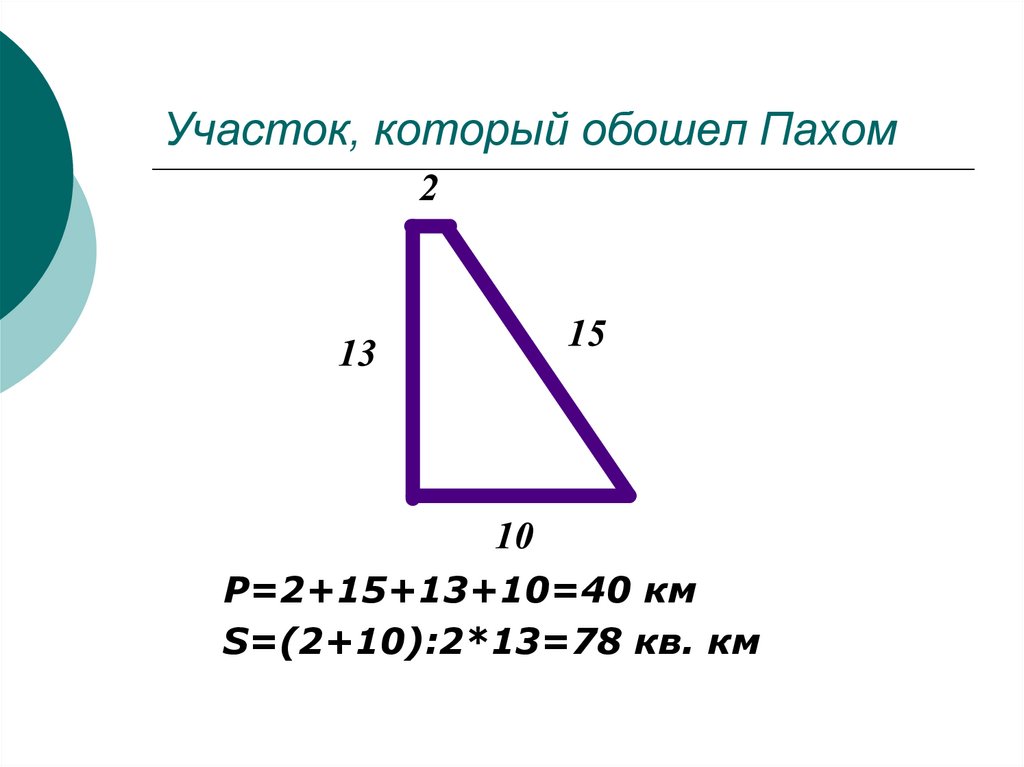
15. Участок, который обошел Пахом
P=2+15+13+10=40 кмS=(2+10):2*13=78 кв. км
16.
«Особенную важность имеют теметоды науки, которые позволяют
решать задачу, общую для всей
практической деятельности
человека: как располагать своими
средствами для достижения
наибольшей выгоды»
П.Л. Чебышев
17. Задачи на оптимизацию.
Оптимизация,(от лат. optimum- наилучший).
Выбор наилучшего из возможных
вариантов.
18. Цели урока
Знать алгоритм решенияпрактических задач на
оптимизацию;
Уметь применять алгоритм поиска
наибольшего и наименьшего
значений функции в решении
задач;
Осознать, насколько в жизни
важны и необходимы
математические знания.
19. Схема решения задач на оптимизацию
Составление математической моделивыбирается независимая переменная, через
которую выражается та величина, для
которой надо найти наибольшее или
наименьшее значение
Работа с моделью
находится наибольшее или наименьшее
значение полученной функции
Ответ на вопрос задачи
по результатам, полученным в предыдущем
пункте, записывается конкретный ответ на
вопрос задачи
20.
Периметр прямоугольника равен 40 см.Какую длину должны иметь стороны
прямоугольника, чтобы площадь была
наибольшей?
21. Задача: Периметр прямоугольника равен 40 см. Какую длину должны иметь стороны прямоугольника, чтобы площадь была наибольшей?
х20 - х
Решение:
Составляем математическую модель. Пусть
х – ширина прямоугольника, тогда длина –
20 - х. Функция будет иметь следующий вид:
S(x) = x • (20 - x) = 20x - x2 , где 0<x<20
Находим наибольшее значение этой функции
S`(x) = 20 - 2x,
20 – 2x = 0,
x = 10.
S(10) = 10 • (20 - 10) = 100
Ответ:
Длина и ширина прямоугольника равны 10 см.
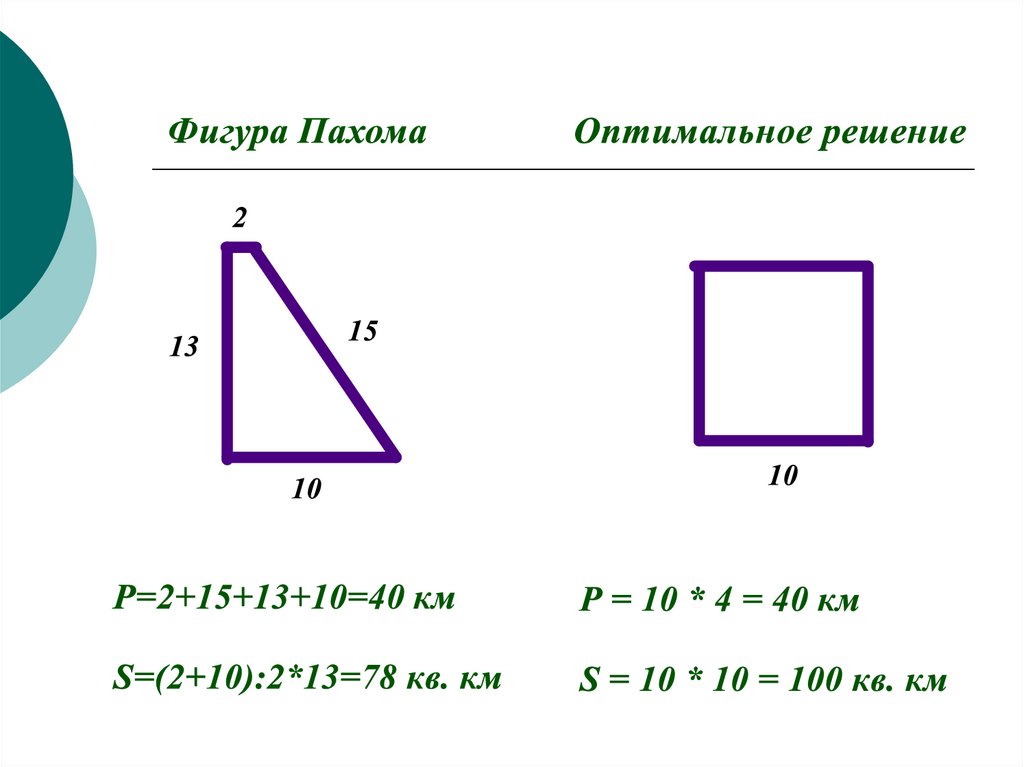
Вывод:
Наибольшую площадь среди четырехугольников
при заданном периметре имеет квадрат
22.
23. Проверка домашнего задания
Пусть MN=X, тогда AM=(12-х)/2. Функция примет
вид V (x) = (12 – x) • х2 / 2
Наибольшее значение эта
функция принимает при
х=8. V(8)=128 куб.см
Вывод:
объём коробки будет
наибольшим при длине
основания равном 8 см
24.
25. Задача Открытый металлический бак с квадратным основанием должен вмещать 32 л воды. При каких размерах на его изготовление
уйдётнаименьшее количество металла?
26.
Решение:Пусть х – длина основания, тогда высота – 32 / х2.
Площадь поверхности состоит из дна и четырёх
боковых прямоугольников
S= х2 + 4х • 32 / х2 = х2 +128/х
S`=2х – 128/х2 2х3 - 128 = 0 х3 = 64 х = 4
х=4 – единственная точка минимума на отрезке,
значит в ней функция принимает наименьшее
значение.
Ответ: наименьшее количество металла
потребуется для бака с размерами 4х4х2 дм.
27. Задача
Строители решили пристроить кстене школы физкультурный зал
прямоугольной формы. Оказалось,
что кирпича у них хватит на 100 м
стены (по периметру трёх новых
стен). Зал должен быть как можно
больше по площади.
Какие размеры пристройки
выбрать?
28. Решение задач в группах.
1 группа.Сумма двух целых чисел равна 24. Найдите
эти числа, если известно, что их произведение
принимает наибольшее значение.
2 группа.
Число 54 представьте в виде суммы трёх
положительных слагаемых, два из которых
пропорциональны числам 1 и 2, таким образом,
чтобы произведение всех слагаемых было
наибольшим.
3 группа.
Для стоянки машин выделили площадку
прямоугольной формы, примыкающую одной
стороной к стене здания. Площадку обнесли с
трех сторон металлической сеткой длиной
200 м, и площадь ее при этом оказалась
наибольшей. Каковы размеры площадки?
29. Ответы
1 группа. (12; 12).2 группа. (12, 24, 18 )
3 группа. (50, 100, 50)
30.
Однажды в разговоре П.Л. Чебышевзаметил: «В старину математические
задачи задавали боги. Далее
наступил второй период, когда
задачи задавали полубоги: Ньютон,
Эйлер, Лагранж и т.д. Теперь
третий период, когда задачи задает
практика»
31. Домашнее задание.
1 группа – учебник:задачи № 312, 315.
2 и 3 группа -
творческое
задание. Составить вместе с
родителями и оформить решение
в тетради задачу на оптимизацию,
с которой вам или вашим
родителям пришлось столкнуться
на практике.





























 Математика
Математика








