Декада естествознания (физика)

1.

Декада естествознания
(физика)
ЗАСЕДАНИЕ
ЛОНДОНСКОГО
КОРОЛЕВСКОГО
ОБЩЕСТВА

2.

ПРЕДСЕДАТЕЛЬ ЛОНДОНСКОГО
КОРОЛЕВСКОГО ОБЩЕСТВА
КРИСТОФЕР РЕН
КЕМБРИДЖ. Национальная библиотека

3.

4.

ИСТОРИЧЕСКАЯ СПРАВКА
Лондонское королевское общество – одно из
старейших в мире научных обществ; оно создано 28
ноября 1660 г. и утверждено Королевской хартией в
1662 г. Одним из инициаторов создания Общества
был Р. Бойль; важную роль в создании Лондонского
королевского общества сыграл призыв Ф. Бэкона к
экспериментальному изучению природы. Девиз
Лондонского королевского общества – Nullius in
verba (ничего на словах) – указывал на то, что в
качестве доказательства общество должно
признавать только эксперимент (происхождение
девиза часто возводят к стиху Горация Nullius
addictus iurare in verba magistri – клятвы слова
повторять за учителем не присужденый)

5.

НА СЕГОДНЯШНЕМ ЗАСЕДАНИИ МЫ
РАСМОТРИМ ВОПРОС О ДВИЖЕНИИ
НЕБЕСНЫХ ТЕЛ В ПОЛЕ СИЛЫ ТЯГОТЕНИЯ
ДРУГИХ ТЕЛ.ОСНОВНОЙ ПРОБЛЕМОЙ
ЯВЛЯЕТСЯ ВЫЯСНЕНИЕ ВИДА ТРАЕКТОРИИ
ДВИЖЕНИЯ НЕБЕСНОГО ТЕЛА В ПОЛЕ
ТЯГОТЕНИЯ. НА ЗАСЕДАНИЕ ЛОНДОНСКОГО
КОРОЛЕВСКОГО ОБЩЕСТВА БЫЛИ
ПРИГЛАШЕНЫ УЧЕНЫЕ, ЧТОБЫ РАССКАЗАТЬ
О СВОИХ ИДЕЯХ ОТНОСИТЕЛЬНО РЕШЕНИЯ
ПОСТАВЛЕННОЙ ЗАДАЧИ. СРЕДИ НИХ:

6.

Джованни Борелли - ученик Галилея,
естествоиспытатель.

7.

Роберт Гук - один из основателей Лондонского
Королевского общества.

8.

Эдмунд Галлей - астроном, секретарь Лондонского
королевского общества.

9.

Исаак Ньютон - астроном, математик.

10.

В связи с этим одной из задач нашего
собрания является сопоставление
теоретических выкладок ученых с опытными
данными астрономов.
В дискуссии мы будем использовать
гелиоцентрическую систему мира Коперника,
и все рассуждения должны быть согласованы
с этой системой мира.
Первым высказать свои идеи приглашается
Джованни Борелли.

11.

Мой учитель – Галилей – частично решил
поставленную задачу , изучая законы свободного
падения тел у поверхности Земли . Он
рассматривал полеты тел ,
Брошенных у поверхности Земли с различными
начальными скоростями. При этом он
рассматривал малые расстояния так, что участок
Земли, где было брошено тело можно было
считать плоскостью. Он показал ,что все тела ,
независимо от их массы , движутся с одним и тем
же ускорением g = 9,8 м/с2,
направленным вниз , а траекторией движения
является парабола.

12.

Направим ось ОХ вдоль
Земли, а ось ОУ вниз. В
качестве начальной
точки возьмем точку
бросания тела. Пусть
начальная скорость
направлена
горизонтально. Тогда
уравнения движения
выглядят так:
/
х = vºt; у = gt2 2

13.

Выражаем время из первого уравнения и
подставляем во второе . Получаем уравнение
траектории движения :
y=
g
2
0
2V
*x
2

14.

Графиком уравнения является парабола ,
Следовательно, и траекторией движения
будет парабола . Что касается тяготения,то мой
учитель считал, что никакой такой силы не
существует, то есть небесные тела не
взаимодействуют друг с другом . Они движутся
по окружности вокруг более тяжелого небесного
тела .
Таким образом , Галилей говорил о двух видах
траектории:
1)параболе (если тело движется у поверхности
планеты );
2)окружности ( если более легкое тело
находится далеко от более тяжелого тела )

15.

Сам я думаю , что должно
существовать притяжения более легкого
к более тяжелому телу . Сила такого
тяготения должна быть приложена к
центру масс более легкого тела и
направлена к центру масс более
тяжелого тела.

16.

Направим ось Ох вдоль
Земли , а ось Оy
вниз . В качестве
начальной точки
возьмем точку
бросания тела. Пусть
начальная скорость
направлена
горизонтально. Тогда
Уравнения движения
тела выглядят так :
X= V0t
y= g t2 / 2

17.

ДОКЛАД РОБЕРТА ГУКА…

18.

В 1676 году я написал письмо Ньютону, в
котором изложил свои идеи по поводу решения
проблемы траекторий движения в поле тяготения в
качестве основных положений я взял следующие
утверждения.

19.

20.

Земля
Земля
F
r
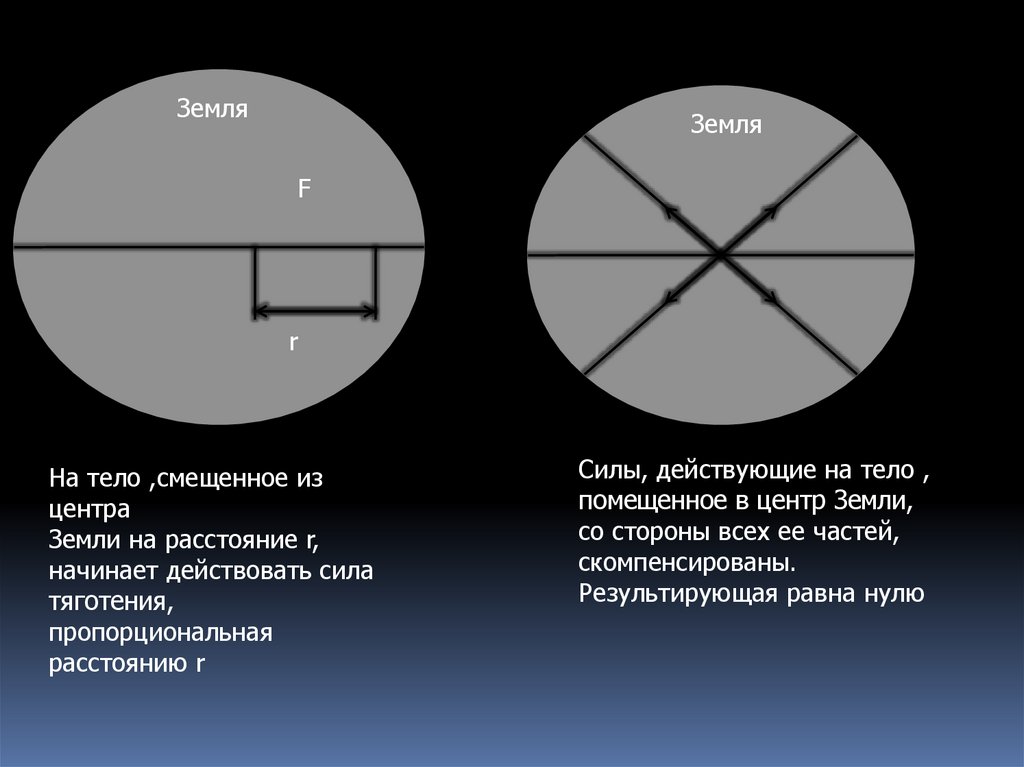
На тело ,смещенное из
центра
Земли на расстояние r,
начинает действовать сила
тяготения,
пропорциональная
расстоянию r
Силы, действующие на тело ,
помещенное в центр Земли,
со стороны всех ее частей,
скомпенсированы.
Результирующая равна нулю

21.

Доклад ученика Кеплера.
Используя многолетние наблюдения за
движением планет(в особенности
Марса),мой учитель – Иоганн Кеплер –
установил , что планеты обращаются
вокруг Солнца по окружности. Он
сформулировал три закона движения
планет , которые с большой точностью
подтверждаются астрономическими
измерениями.

22.

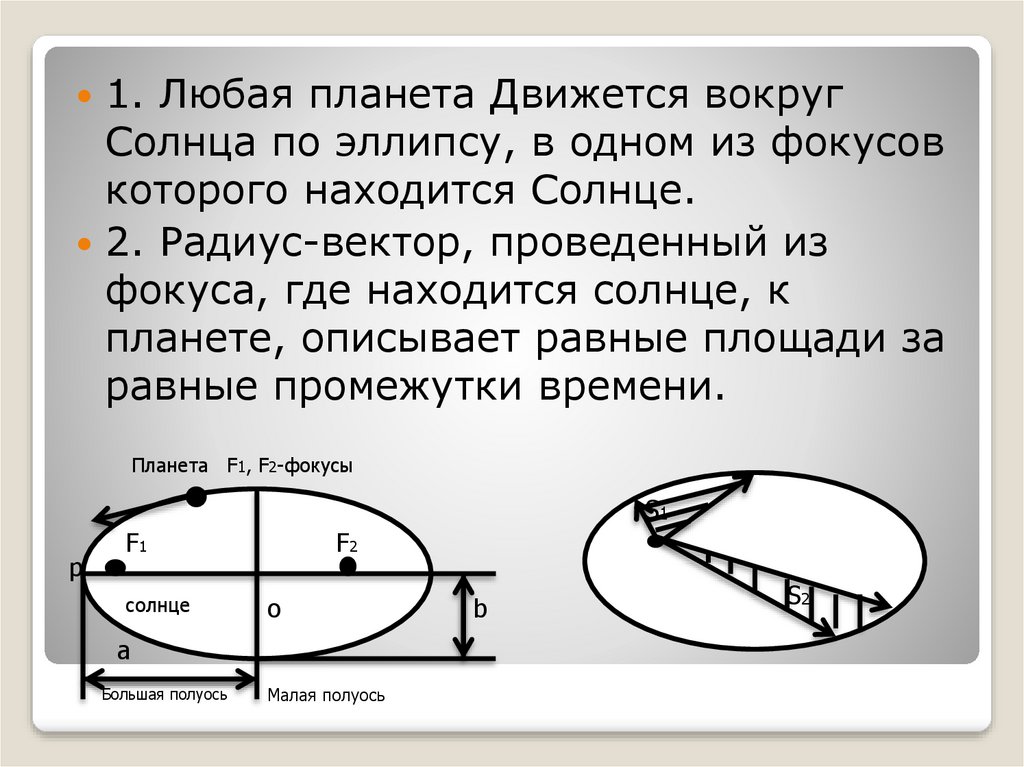
1. Любая планета Движется вокруг
Солнца по эллипсу, в одном из фокусов
которого находится Солнце.
2. Радиус-вектор, проведенный из
фокуса, где находится солнце, к
планете, описывает равные площади за
равные промежутки времени.
Планета F1, F2-фокусы
S1
p
F1
солнце
F2
o
a
Большая полуось
Малая полуось
b
S2

23.

24.

Планета
Расстояние
до Солнца,
а (в
астромических ед.)
Период
вращения,
Т (в годах)
Меркурий
0.30
0.16
1.05
Венера
0.76
0.67
0.98
Земля
1
1
1.00
Марс
1.52
1.88
0.99
Юпитер
5.2
11.86
0.99
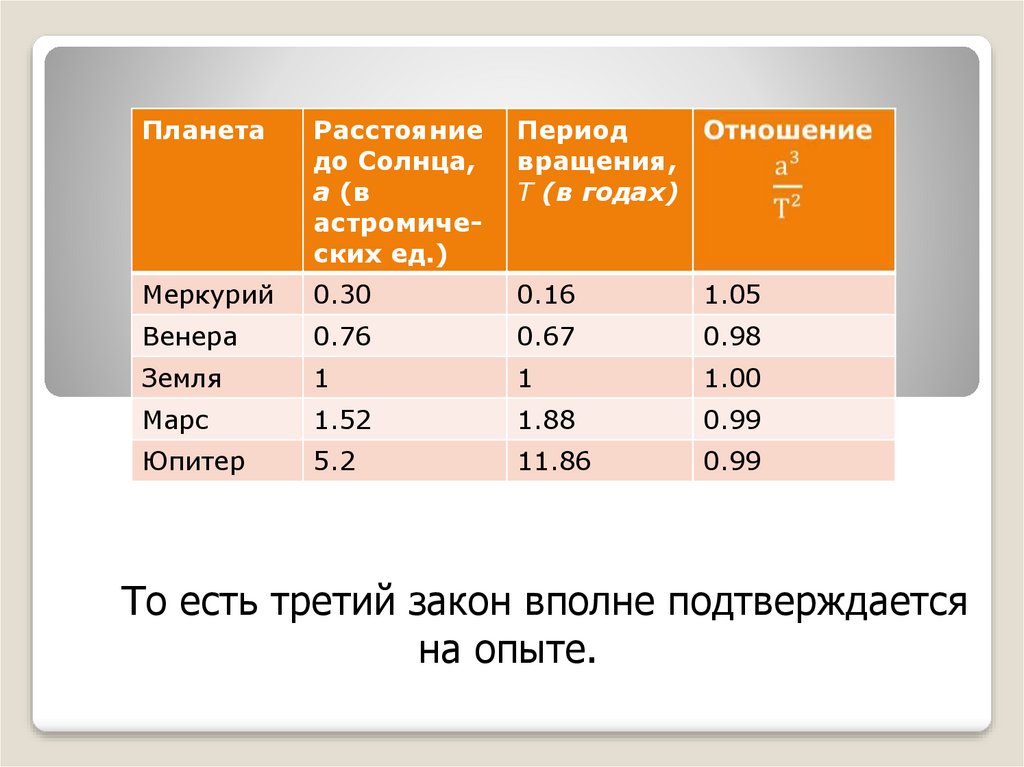
То есть третий закон вполне подтверждается
на опыте.

25.

26.

27.

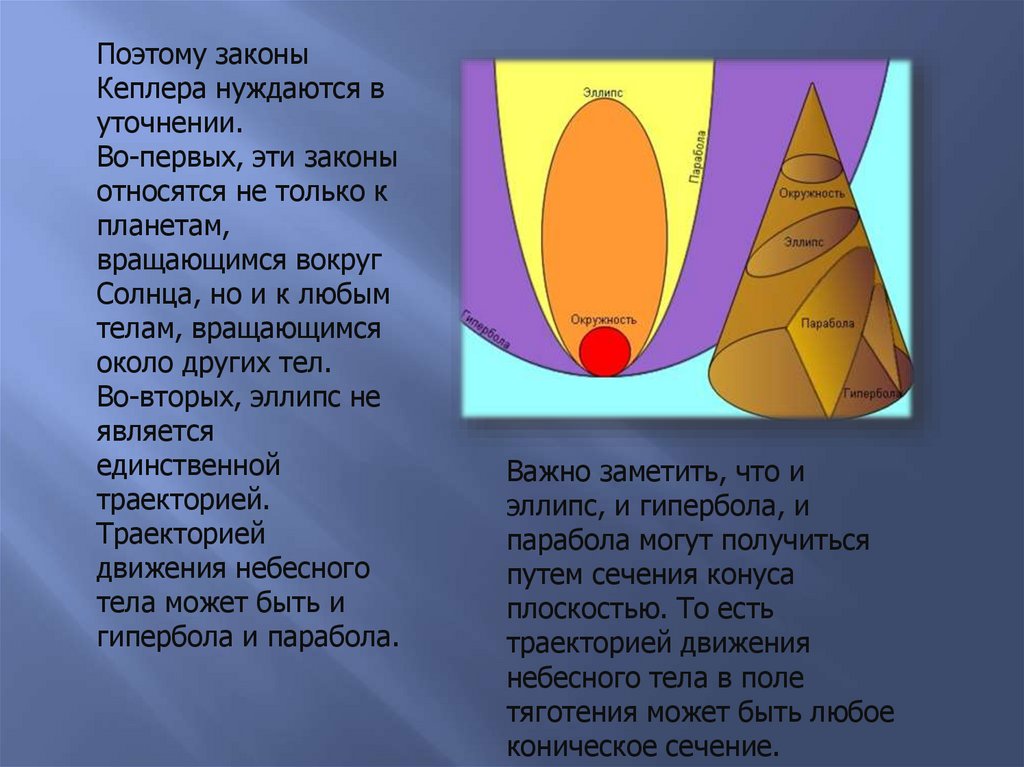
Поэтому законы
Кеплера нуждаются в
уточнении.
Во-первых, эти законы
относятся не только к
планетам,
вращающимся вокруг
Солнца, но и к любым
телам, вращающимся
около других тел.
Во-вторых, эллипс не
является
единственной
траекторией.
Траекторией
движения небесного
тела может быть и
гипербола и парабола.
Важно заметить, что и
эллипс, и гипербола, и
парабола могут получиться
путем сечения конуса
плоскостью. То есть
траекторией движения
небесного тела в поле
тяготения может быть любое
коническое сечение.

28.

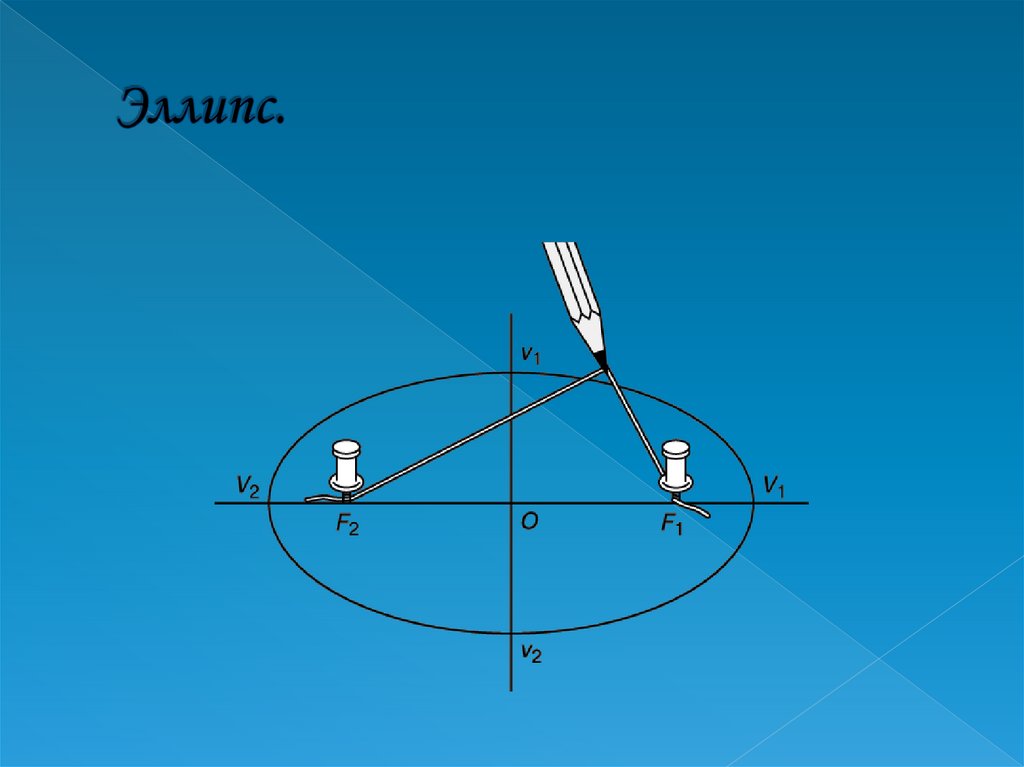
Эллипс – замкнутая кривая, то есть тело,
движущееся вокруг Солнца (или планеты) по
эллипсу, связано с Солнцем (или с планетой
соответственно). Поэтому полная механическая
энергия тела, движущегося по эллипсу, меньше
нуля.
Парабола и гипербола – разомкнутые кривые, то
есть тело, движущееся вокруг Солнца (или
планеты) по этим кривым, не связано с ним.
Поэтому полная механическая энергия тела,
движущегося по гиперболе или параболе, больше
либо равна нулю.
E ‹ 0, система является связанной, траекторией является
эллипс.
E ≥ 0, система не является связанной, траекторией является
или парабола, или гипербола.

29.

Таким образом, пока энергия спутника
Солнца (или планеты) меньше нуля,
спутник связан с Солнцем (или планетой)
и движется по эллипсу. Как только
энергия спутника возрастает до нуля,
тело прекращает быть связанным с
Солнцем (или планетой) и движется по
параболе или по гиперболе.

30.

31.

Конические сечения - это кривые, получившиеся в сечении конуса
плоскости. Также кривых может получиться три.
Если секущая плоскость пересекает всю поверхность конуса, то в
сечение получается эллипс.
Если секущая плоскость пересекает часть поверхности конуса и
не параллельна, ни одной образующих конуса, то в сечение
получается гипербола
Если секущая плоскость пересекается в одной из образующих
конуса, то в сечение получается парабола.

32.

33.

Трактаты о конических сечениях,
написанные Аристотелем и Евклидом в
конце 4 в. до н.э., были утеряны, но
материалы из них вошли в знаменитые
Конические сечения Аполлония
Пергского (ок. 260–170 до н.э.), которые
сохранились до нашего времени.
Аполлоний отказался от требования
перпендикулярности секущей плоскости
образующей конуса и, варьируя угол ее
наклона, получил все конические сечения
из одного кругового конуса, прямого или
наклонного. Аполлонию мы обязаны и
современными названиями кривых –
эллипс, парабола и гипербола.

34.

Одну ветвь гиперболы (PV1Q) мы вычерчиваем, следя
за тем, чтобы нить оставалась все время натянутой,
и потягивая оба конца нити вниз за точку F2, а когда
точка P окажется ниже отрезка F1F2, придерживая
нить за оба конца и осторожно отпуская ее. Вторую
ветвь гиперболы мы вычерчиваем, предварительно
поменяв Ветви гиперболы приближаются к двум
прямым, которые пересекаются между ветвями. Эти
прямые, называемые асимптотами гиперболы.
Угловые коэффициенты этих прямых равны где –
отрезок биссектрисы угла между асимптотами,
перпендикулярной отрезку F2F1; отрезок v1v2
называется сопряженной осью гиперболы, а отрезок
V1V2 – ее поперечной осью. Таким образом,
асимптоты являются диагоналями прямоугольника
со сторонами, проходящими через четыре точки v1,
v2, V1, V2 параллельно осям. Чтобы построить
этот прямоугольник, необходимо указать
местоположение точек v1 и v2. Они находятся на
одинаковом расстоянии.

35.

Парабола. Фокусы эллипса и гиперболы были
известны еще Аполлонию, но фокус параболы, повидимому, впервые установил Папп (вторая пол.
III в.), определивший эту кривую как
геометрическое место точек, равноудаленных от
заданной точки (фокуса) и заданной прямой,
которая называется директрисой. Построение
параболы с помощью натянутой нити, основанное
на пределе Другие свойства. Свойства конических
сечений поистине неисчерпаемы, и любое из них
можно принять за определяющее. Важное место в
Математическом собрании Паппа (ок. 300),
Геометрии Декарта (1637) и Началах Ньютона
(1687) занимает задача о геометрическом месте
точек относительно четырех прямых. Если на
плоскости заданы четыре прямые L1, L2, L3 и L4
(две из которых могут совпадать) и точка P
такова, что произведение расстояний от P до L1 и
L2 пропорционально произведению расстояний от
P до L3 и L4, то геометрическое место точек P
является коническим сечением.

36.

Две пересекающиеся
прямые образуют
вырожденную гиперболу .
Два вырожденных эллипса
возникают, когда конус
пересекается с
плоскостью, параллельной
его основанию.

37.

38.

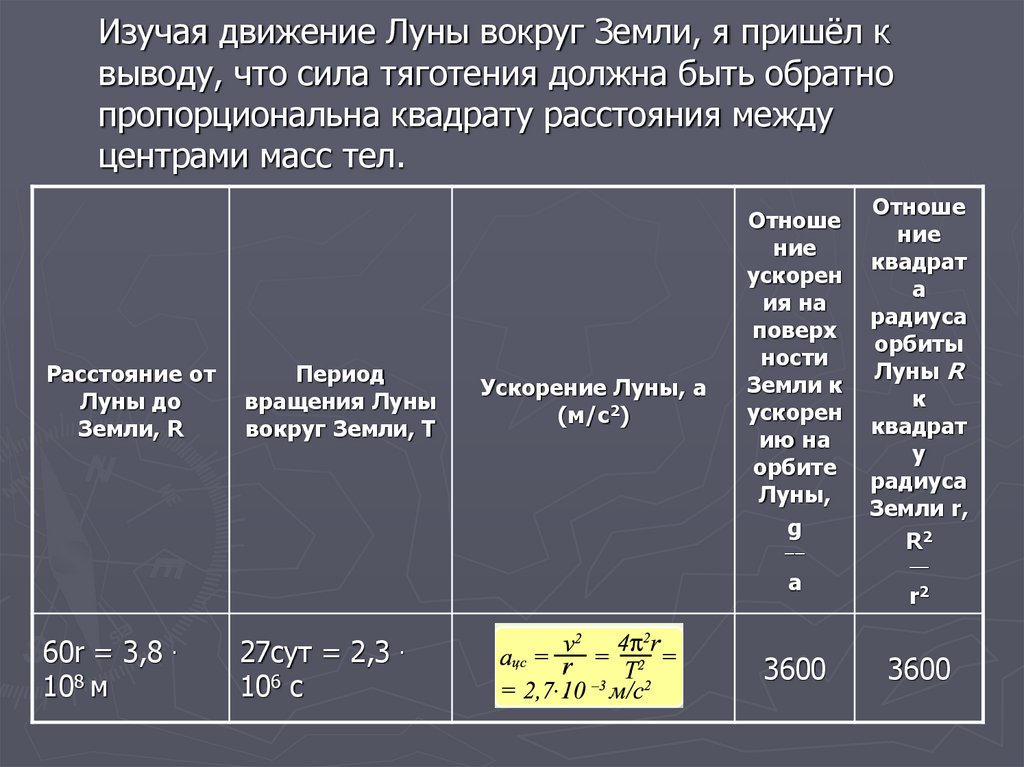
Изучая движение Луны вокруг Земли, я пришёл к
выводу, что сила тяготения должна быть обратно
пропорциональна квадрату расстояния между
центрами масс тел.
Расстояние от
Луны до
Земли, R
Период
вращения Луны
вокруг Земли, Т
Ускорение Луны, а
(м/с2)
Отноше
ние
ускорен
ия на
поверх
ности
Земли к
ускорен
ию на
орбите
Луны,
g
__
a
60r = 3,8 .
108 м
27сут = 2,3 .
106 с
3600
Отноше
ние
квадрат
а
радиуса
орбиты
Луны R
к
квадрат
у
радиуса
Земли r,
R2
__
r2
3600

39.

Траекторией вращения Луны является
окружность. На Луну действует сила
тяготения со стороны Земли Fтяж. По
основному закону динамики:
ma = Fтяг1.
У поверхности Земли на Луну бы действовала
сила тяготения Fтяг2 отличная от Fтяг1 . По
основному закону динамики,
ma2 = Fтяг2.

40.

Если бы Луна свободно падала на поверхности
Земли, то её ускорение было бы равно
a2 = g = 9,8 м/с2
Поэтому сила тяготения у поверхности Земли
равна:
mg = Fтяг
Найдём отношение силы, с которой Луна
притягивалась бы на поверхность Земли, к силе,
с которой она притягивается к Земле на своей
орбите:

41.

Сила тяготения обратно пропорциональна квадрату
расстояния до Луны. В 1м случае это расстояние
равно радиусу орбиты луны R, а во 2м – радиусу
Земли r.
Из этого мы предположим, что сила тяготения, с
которой тела притягиваются друг к другу, обратно
пропорциональна квадрату расстояния между телами.
Также она должна быть пропорциональна массам
обоих тел.

42.

Основываясь на трёх законах динамики и
формуле силы тяготения, я построил теорию
движения небесных тел в поле тяготения.
И так, докажем 3ий закон Кеплера. Пусть M –
масса Солнца, а m – масса планеты. Пусть
она движется по окружности радиуса R,
тогда она имеет центростремительное
ускорение, равное:
На планету действует сила тяготения со
стороны Солнца, равная

43.

По основному закону динамики, ma = Fтяг.
Тогда

44.

Отношение куба радиуса окружности, по которой
движется планета, к квадрату периода
вращения одинаково для всех планет
Солнечной системы, т.к. оно не зависит от
массы планеты.
Вычислим скорость V 1 при которой тело
начинает двигаться по окружности и
становится спутником.

45.

Таким образом, тело, брошенное на планете
(или Солнце) со скоростью, меньшей скорости
V1, двигаясь по эллипсу, в одном из фокусов
которого находится центр планеты, упадёт на
поверхность планеты. Это связано с тем, что
эллипс замыкается внутри планеты.

46.

Как только начальная скорость тела
становится равной V1, эллипс переходит в
окружность, которая замыкается вне планеты.
Тогда тело станет спутником и будет
двигаться по этой окружности вокруг планеты
(или Солнца).

47.

Если начальная скорость тела будет превышать
V1 , траекторией тела будет эллипс, в одном из
фокусов которого будет планета (или Солнце).

48.

Вычислим скорость V2 , при которой траектория тела
разомкнётся и тело перестанет быть спутником
планеты (или Солнца), т.е. тело перестанет быть
связанным с планетой.
Пусть тело запускается с расстояния R от центра
планеты. При этом полная механическая энергия тела
больше либо равна нулю:

49.

То есть при начальной скорости V = V2 тело
начинает двигаться по разомкнутой прямой.
Причём при скорости, равной V2, тело движется
по параболе, а при скорости V > V2 тело
движется по гиперболе. При этом тело уже не
будет связано с планетой и потому не будет её
спутником.

50.

Все планеты Солнечной системы имеют скорость
вращения V, лежащую в пределах:
Поэтому планеты движутся вокруг Солнца по
эллипсам, в одном из фокусов которых
находится Солнце. Это подтверждает первый
закон Кеплера.

51.

Тело, движущееся по параболе или гиперболе
выходит из поля тяготения планеты и может
стать спутником другой планеты или Солнца.

52.

Джованни Борелли
Галилео Галилей

53.

54.

55.

56.

В своем трактате
«Притяжение Земли» Гук указал
неверную зависимость силы
тяготения от расстояния между
телами:
Телескоп Р.Гука
Fтяг = Kr

57.

Барометр Р.Гука
так как на бесконечном
расстоянии получается
бесконечно большая сила
притяжения, что
противоречит опыту: чем
дальше тела, тем они слабее
притягиваются.

58.

59.

Кеплер утверждал, что
планеты движутся вокруг
Солнца по эллипсам.

60.

Но наблюдение показывают ,что
возможны и другие траектории
движения небесных тел, такие как
парабола и гипербола.

61.

Итак, мы заслушали выступления участников
нашего общества и замечания к ним.
Объявляю сегодняшнее заседание общества
закрытым.