Простейшие задачи в координатах

1.

13.Вектор, конец которого совпадает с
данной точкой, а начало – с … координат,
называется … – … данной точки

2.

13.Вектор, конец которого совпадает с
данной точкой, а начало – с началом
координат, называется радиус – вектором
данной точки
14.Координаты любой точки равны …
координатам её радиус – вектора

3.

14.Координаты любой точки равны
соответствующим координатам её радиус –
вектора
М(x;y;z) OM x; y; z
М
О

4.

15.Каждая координата вектора равна …
соответствующих координат его … и …
А( х1; у1; z1 ), B( x2 ; y2 ; z2 )
АВ ... ...;... ...;... ...
В
А

5.

15. Каждая координата вектора равна
разности соответствующих координат его
конца и начала
А( х1; у1; z1 ), B( x2 ; y2 ; z2 )
АВ x2 х1 ; y2 у1 ; z 2 z1
В
А

6.

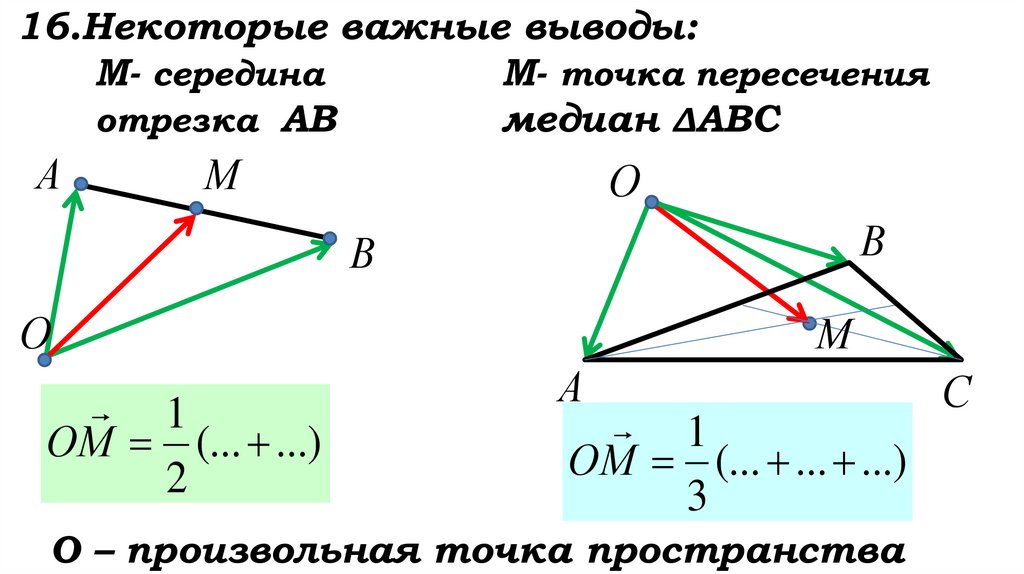
16.Некоторые важные выводы:
М- середина
М- точка пересечения
отрезка АВ
медиан ΔАВС
А
М
О
В
В
О
1
ОМ (... ...)
2
М
А
1
ОМ (... ... ...)
3
О – произвольная точка пространства
С

7.

16.Некоторые важные выводы:
М- середина
М- точка пересечения
отрезка АВ
медиан ΔАВС
А
М
О
В
В
О
1
ОМ (ОА ОВ)
2
М
А
С
1
ОМ (ОА ОВ ОС )
3
О – произвольная точка пространства

8.

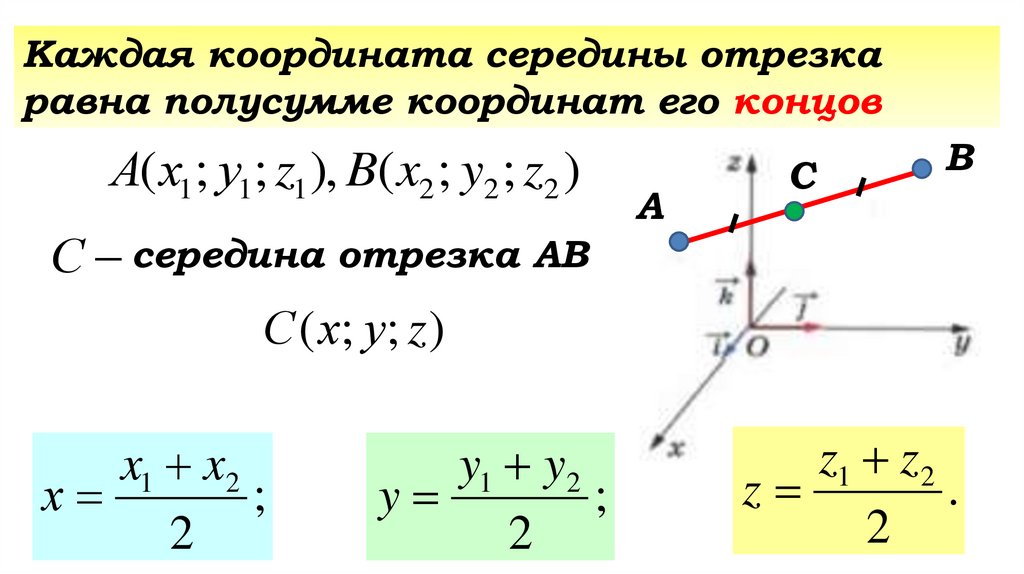
Стр.106. п.49. задача а)
Каждая координата середины отрезка
равна полусумме координат его концов
А( х1; у1; z1 ), B( x2 ; y2 ; z2 )
С
С середина отрезка АВ
А
В

9.

Стр.106. п.49
Каждая координата середины отрезка
равна полусумме координат его концов
А( х1; у1; z1 ), B( x2 ; y2 ; z2 )
С середина отрезка АВ
С ( х; у; z )
х ...
y ...
z ...
С
А
В

10.

Каждая координата середины отрезка
равна полусумме координат его концов
А( х1; у1; z1 ), B( x2 ; y2 ; z2 )
С середина отрезка АВ
С ( х; у; z )
x1 x2
х
;
2
y1 y2
y
;
2
А
С
В
z1 z 2
z
.
2

11.

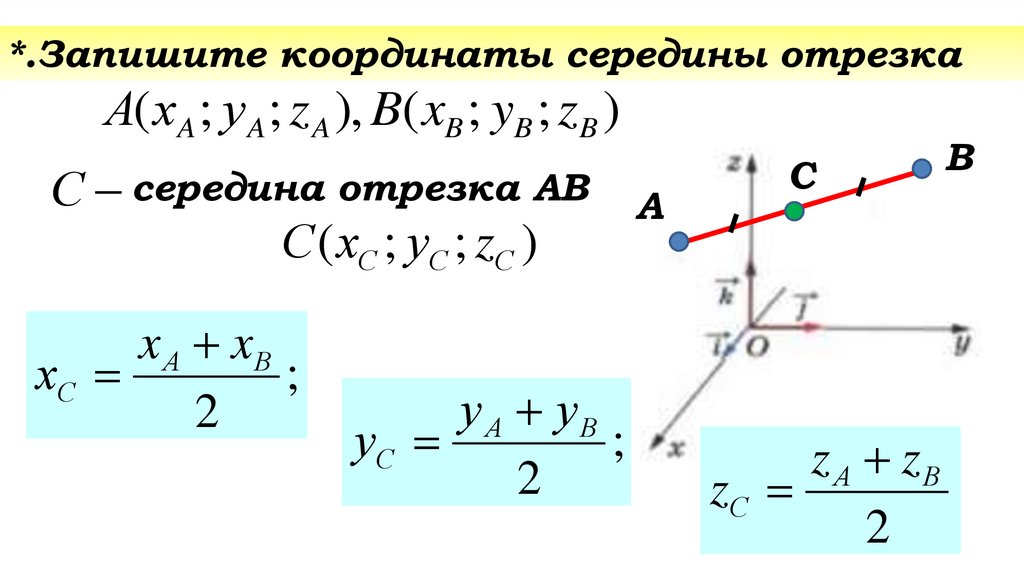
*.Запишите координаты середины отрезка
А( хA ; у A ; z A ), B( xB ; yB ; zB )
С середина отрезка АВ
С ( хС ; уС ; zС )
хС ...
уС ...
А
С
zС ...
В

12.

*.Запишите координаты середины отрезка
А( хA ; у A ; z A ), B( xB ; yB ; zB )
С середина отрезка АВ
С ( хС ; уС ; zС )
x А xВ
хС
;
2
у А уВ
уС
;
2
А
С
z А zВ
zС
2
В

13.

М
Стр.111. №424
середина отрезка АВ, А(0;3; 4), B( 2;2;0)
М ( х; у; z )
а ) х ...
y ...
z ...

14.

М
Стр.111. №424
середина отрезка АВ, А(0;3; 4), B( 2;2;0)
М ( х; у; z )
а ) х 1
y 2,5
z 2
М ( 1;2,5; 2)
Максимум – 3 балла

15.

**
А( хA ; у A ; z A ), B( xB ; yB ; zB )
С середина отрезка АВ
С ( хС ; уС ; zС )
x А xВ
хС
;
2
хВ ...
у А уВ
уС
;
2
уВ ...
z А zВ
zС
2
z В ...

16.

А( хA ; у A ; z A ), B( xB ; yB ; zB )
С середина отрезка АВ
С ( хС ; уС ; zС )
x А xВ
хС
;
2
у А уВ
уС
;
2
z А zВ
zС
2
хВ 2 хС х А
уВ 2 уС у А
z В 2 zС z А

17.

М
Стр.111. №424
середина отрезка АВ, А(14; 8;5), М (3; 2; 7)
В( х; у; z )
б ) х ...
y ...
z ...

18.

М
Стр.111. №424
середина отрезка АВ, А(14; 8;5), М (3; 2; 7)
В( х; у; z )
б ) х 8
y 4
z 19
В( 8;4; 19)
Максимум – 3 балла

19.

Стр.106. п.49. задача б)
Длина вектора а x; y; z вычисляется
по формуле
2
2
2
а x y z
а

20.

Стр.111. №427
а 5; 1;7
2
2
2
а x y z
Выполните самостоятельно

21.

Стр.111. №427
а 5; 1;7
2
2
2
а x y z
2
2
2
а 5 ( 1) 7 75 5 3
Максимум – 2 балла

22.

с i j k
Стр.111. №427
Как предлагаете выполнить задание?
Выполните задание самостоятельно

23.

с i j k
Стр.111. №427
с 1;1;1
2
2
2
с 1 1 1 3
Максимум – 1 балл

24.

Стр.111. №428(а,в,ж)
а 3; 2;1 , b 2;3;1
а) Наметьте ход решения
Выполните решение по схеме:

25.

Стр.111. №428(а,в,ж)
а 3; 2;1 , b 2;3;1 .
а)а b n , n ...
а b ...
Проверка

26.

Стр.111. №428(а,в,ж)
а 3; 2;1 , b 2;3;1 ,
n 1;1;2
а)а b n,
2
2
2
а b 1 1 2 6
Максимум – 1 балл

27.

Стр.111. №428(а,в,ж)
а 3; 2;1 , b 2;3;1 ,
в) Наметьте ход решения
Выполните решение по схеме:

28.

Стр.111. №428(а,в,ж)
а 3; 2;1 , b 2;3;1 ,
в) а b ... ...
Проверка

29.

Стр.111. №428(а,в,ж)
а 3; 2;1 , b 2;3;1 ,
в) а b 14 14 0
Максимум – 1 балл

30.

Стр.111. №428(а,в,ж)
а 3; 2;1 , c 3;2;1 .
ж) Наметьте ход решения
Выполните решение по схеме:

31.

Стр.111. №428(а,в,ж)
а 3; 2;1 , c 3;2;1 .
2а ...;...;.. . , 3c ...;...;.. . .
2а 3с т, т .....
т ...
Проверка

32.

Стр.111. №428(а,в,ж)
а 3; 2;1 , c 3;2;1 .
2а 6; 4;2 , 3c 9;6;3 .
2а 3с т, т 15; 10; 1
т 326
Максимум – 5 баллов

33.

Стр.107. п.49. задача в)
Расстояние между двумя точками
и
вычисляется
М1 ( х1; у1; z1 )
М 2 ( х2 ; у2 ; z2 )
по формуле
d ( x2 x1 ) ( y2 y1 ) ( z2 z1 )
2
2
2

34.

Стр.111. №431(г)
Определите вид треугольника АВС, если
г ) А( 5;2;0), В( 4;3;0), С ( 5;2,2)
Предложите ход решения

35.

Стр.111. №431(г)
Определите вид треугольника АВС, если
г ) А( 5;2;0), В( 4;3;0), С ( 5;2, 2)
2
2
2
2
АВ (...) (...) (...) ....
АС (...) (...) (...) ....
2
2
2
2
ВС (...) (...) (...) ....
2
2
2
2
Треугольник АВС- …, т.к.

36.

Стр.111. №431(г)
Определите вид треугольника АВС, если
г ) А( 5;2;0), В( 4;3;0), С ( 5;2, 2)
2
2
2
2
АВ ( 4 5) (3 2) (0 0) 2
АС ( 5 5) (2 2) ( 2 0) 4
2
2
2
2
ВС ( 5 4) (2 3) ( 2 0) 6
2
2
2
2
Треугольник АВС- прямоугольный, т.к.
ВС АВ АС
2
2
2

37.

Стр.111. №431(г)
Определите вид треугольника АВС, если
ВС АВ АС
2
2
2
ВС АВ АС
2
2
подсказка
ВС АВ АС 2 АВ АС cos A
2
2
2
2

38.

Стр.111. №431(г)
Если:
ВС АВ АС
2
2
ВС АВ АС
2
2
2
2
то треугольник АВС
Тупоугольный
Остроугольный
ВС АВ АС 2 АВ АС cos A
2
2
2
теорема косинусов