Аксиомы стереометрии

1.

24.11.2021

2.

Аксиома.
(от греч. axíõma – принятие положения)
исходное положение
научной теории,
принимаемое без
доказательства

3.

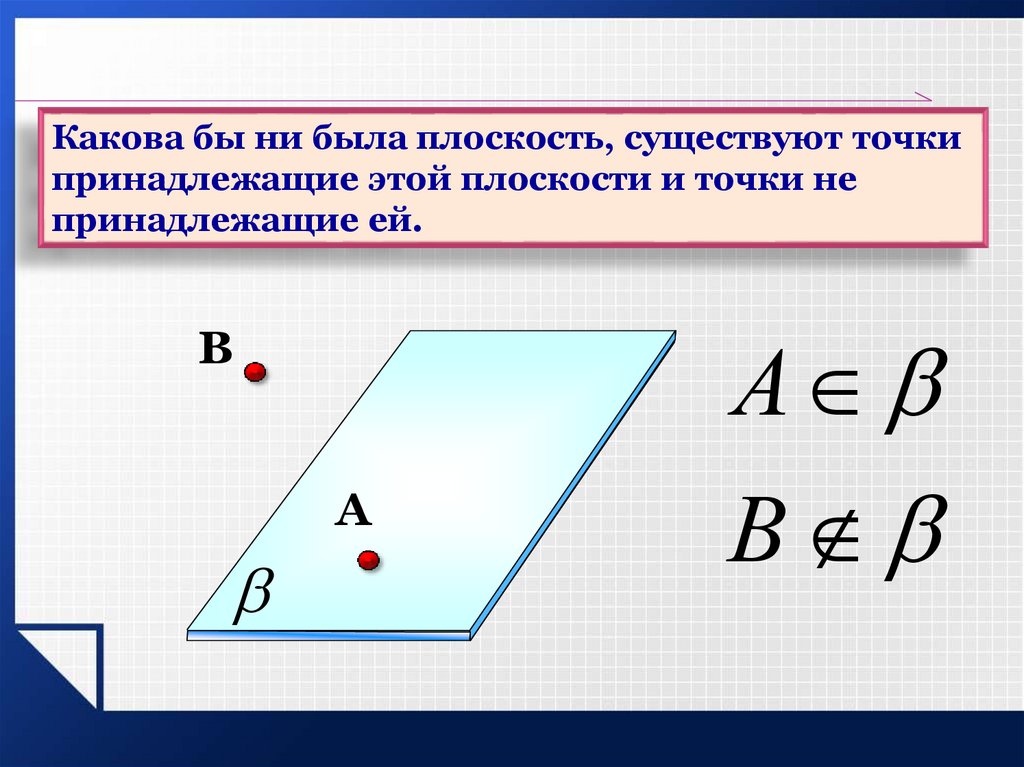
Какова бы ни была плоскость, существуют точки
принадлежащие этой плоскости и точки не
принадлежащие ей.
А
B
A
В

4.

Аксиома А1:
Через три точки, не лежащие на одной прямой,
можно провести плоскость, и притом только одну.
В
А
С

5.

Иллюстрации к теореме из жизни.
Для
видеокамеры,
фотосъемки
для других
Табурет
с тремя ножками
всегдаиидеально
встанет
приборов
часто
используют
– треногу.
Три
на пол и не
будет
качаться. Уштатив
табурета
с четырьмя
ножки
штатива
устойчиво
на любом
ножками
бывают
проблемырасположатся
с устойчивостью,
если
полу
в помещениях,
на асфальте
или прямо
на
ножки
стула не одинаковые
по длине.
Табурет
газоне
на улице,
на пескена
натри
пляже
или ав четвертая
траве в
качается,
т. е. опирается
ножки,
лесу.
Три
ножки штатива
всегда
найдут
плоскость.
ножка
(четвертая
«точка»)
не лежит
в плоскости
пола, а висит в воздухе.

6.

Аксиома А2
Если две точки прямой принадлежат плоскости,
то все точки прямой принадлежит этой
плоскости.
b
С
В
А

7.

Свойство, выраженное в теореме, используется для
проверки «ровности» чертежной линейки. Линейку
прикладывают краем к плоской поверхности стола. Если
край линейки ровный, то он всеми своими точками
прилегает к поверхности стола. Если край неровный, то в
каких-то местах между ним и поверхностью стола
образуется просвет.

8.

Взаимное расположение прямой
и плоскости:
Прямая
лежит в
плоскости.
а
М
а
Множество
общих точек.
Прямая не
пересекает
плоскость. а
Прямая
пересекает
плоскость.
а
а = М
Единственная
общая точка.
а
Нет общих точек.

9.

Аксиома 3:
Если две различные плоскости имеют общую
точку, то они пересекаются по прямой,
проходящей через эту точку.
a
a

10.

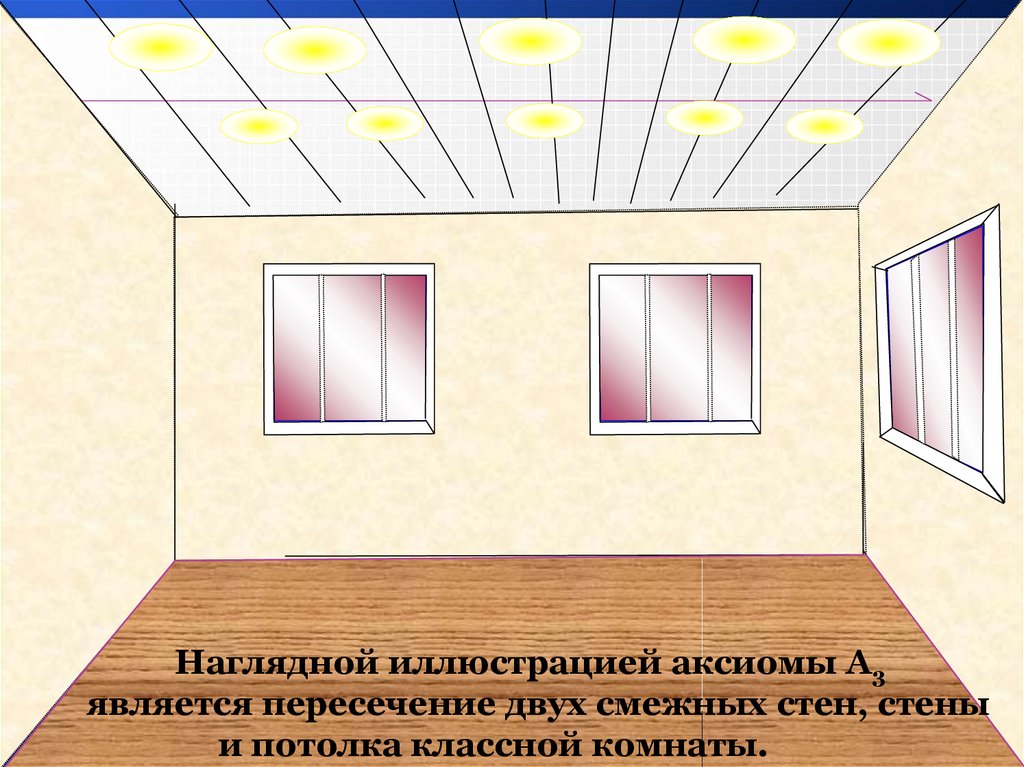
Наглядной иллюстрацией аксиомы А3
является пересечение двух смежных стен, стены
и потолка классной комнаты.

11.

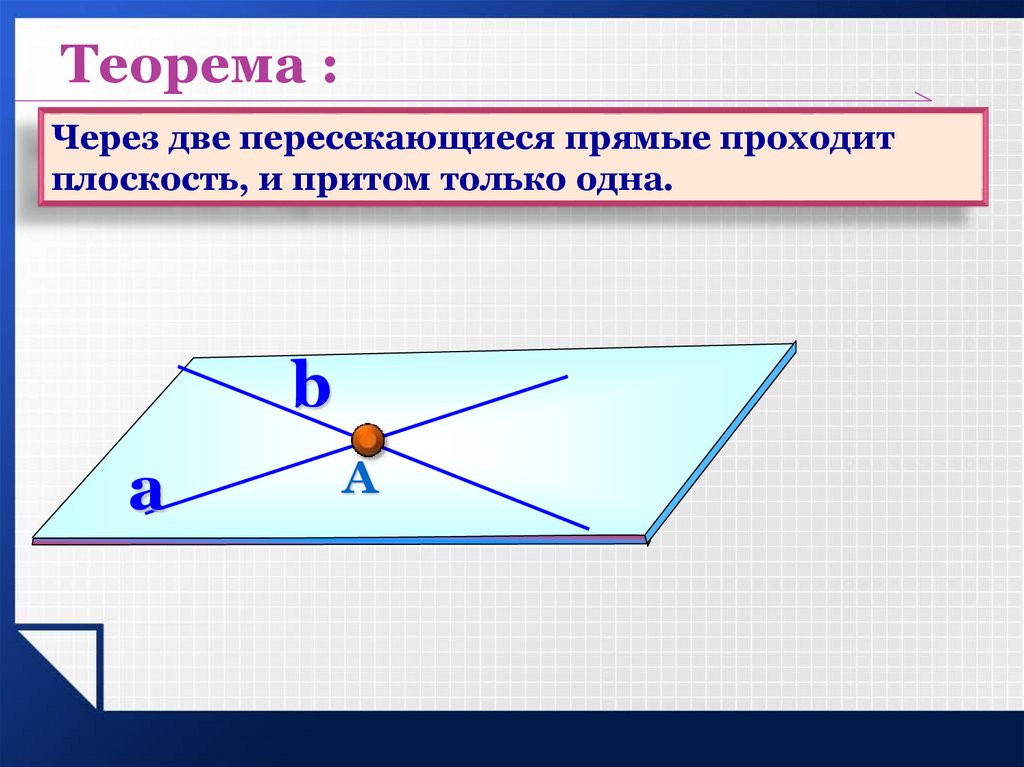
Теорема :
Через две пересекающиеся прямые проходит
плоскость, и притом только одна.
b
a
А

12.

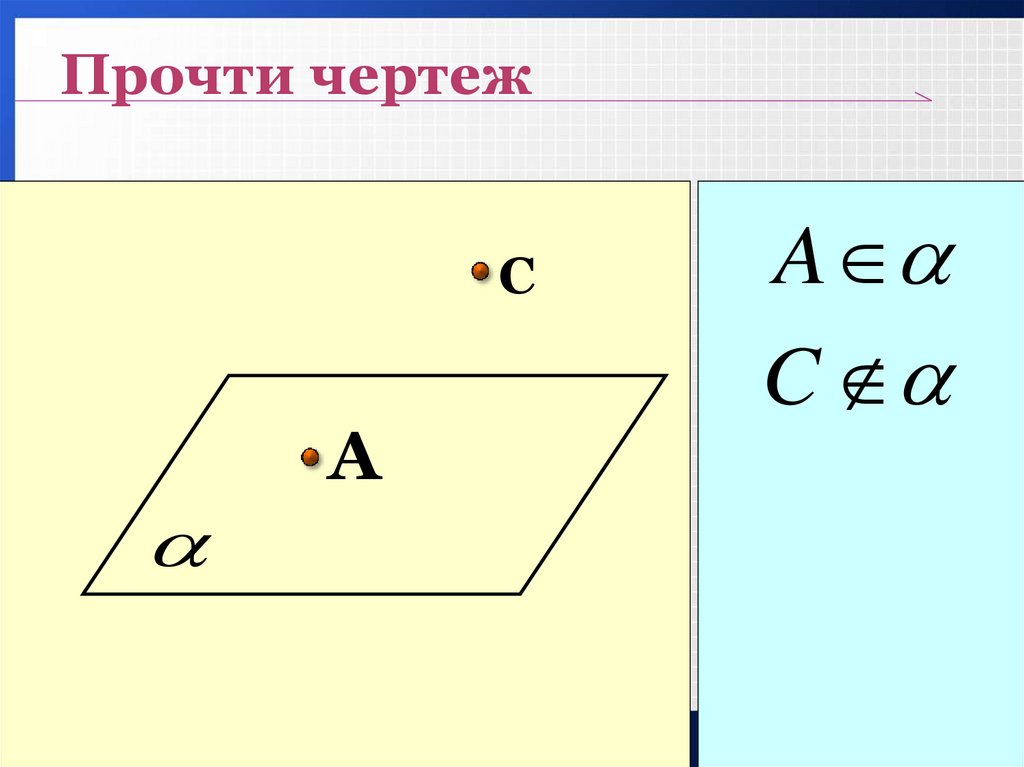
Прочти чертеж
С
A
A
C

13.

Прочти чертеж
b
B
c
a
b B
a
c

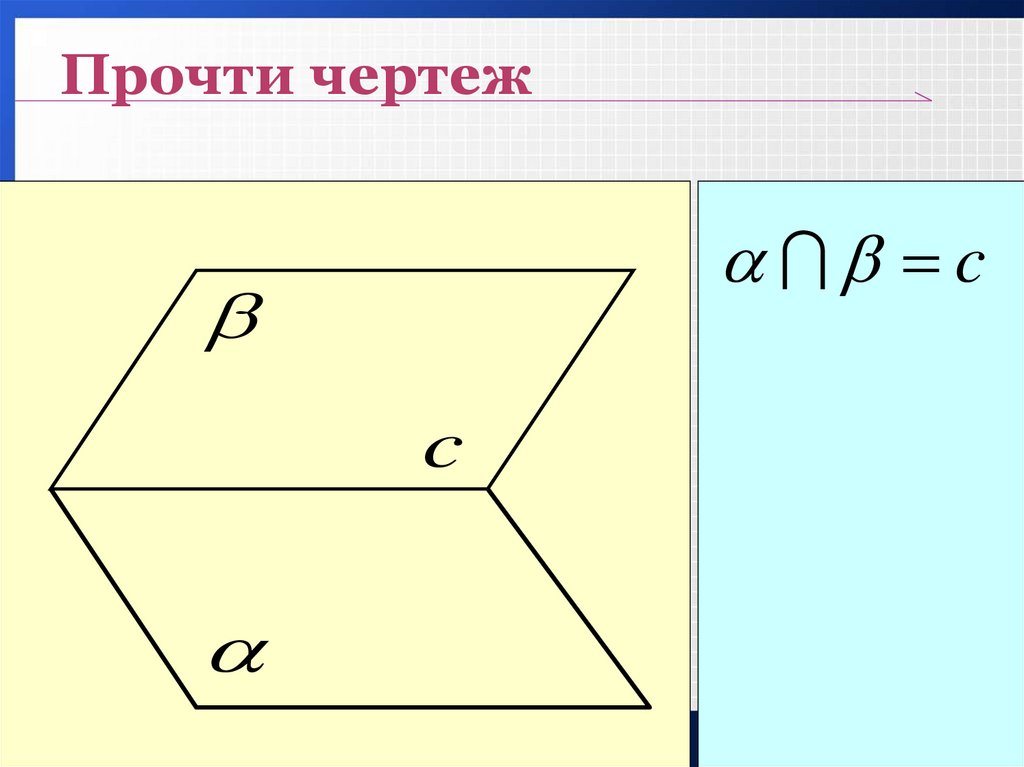
14.

Прочти чертеж
c
c

15.

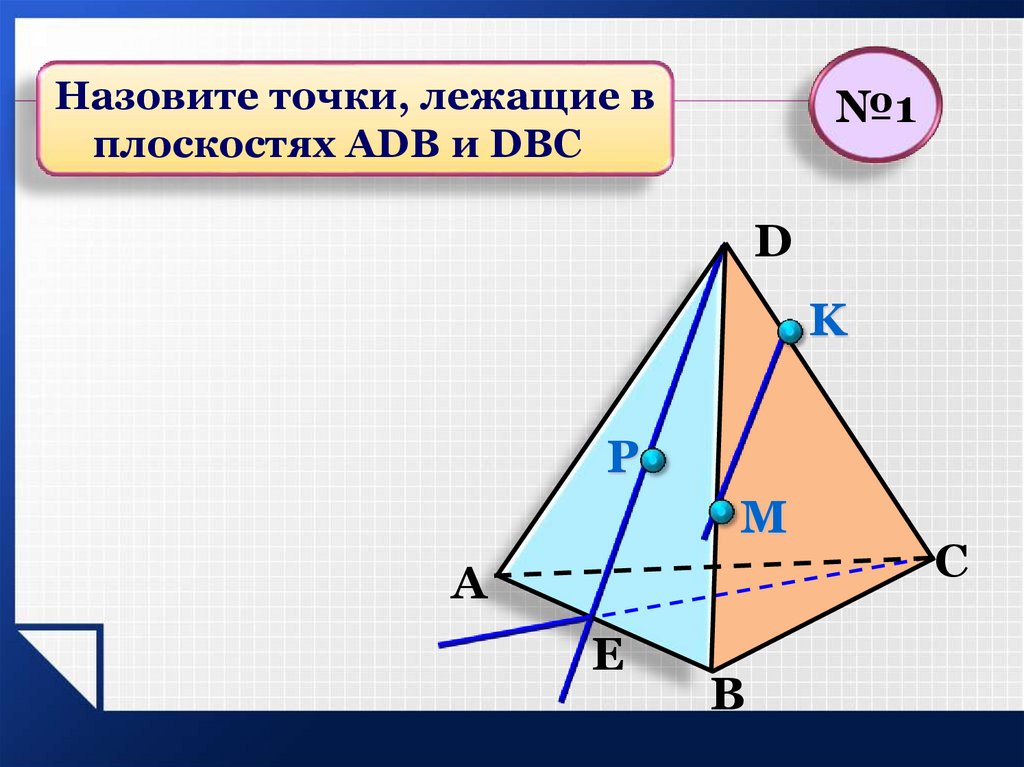
Назовите точки, лежащие в
плоскостях АDB и DBC
№1
D
K
P
M
A
E
B
C

16.

Назовите точки, лежащие в
плоскостях DCC1 и BQC
B1
№2
Q
P
A1
C1
D1
M
K
R
B
A
C
D

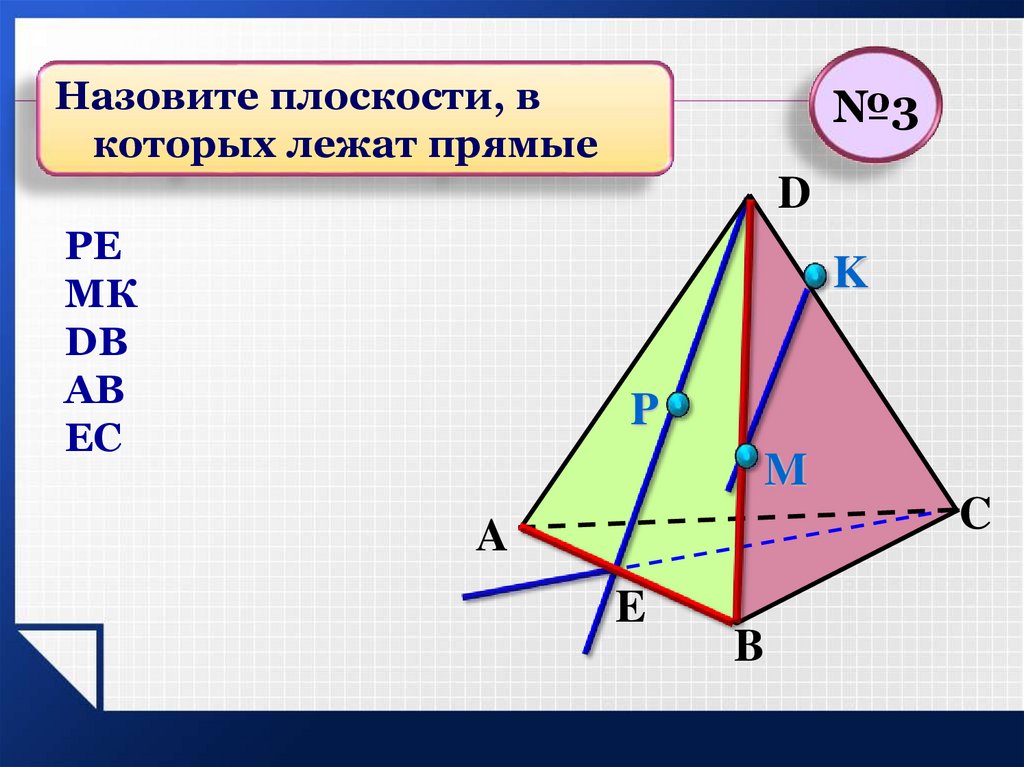
17.

Назовите плоскости, в
которых лежат прямые
№3
D
РЕ
МК
DB
AB
EC
K
P
M
C
A
E
B

18.

Назовите плоскости, в
которых лежит прямая АА1
B1
№4
Q
P
A1
C1
D1
M
K
R
B
A
C
D

19.

Назовите точки пересечения
прямой DK с плоскостью АВС,
прямой СЕ с плоскостью АDB.
№5
D
K
P
M
C
A
E
B

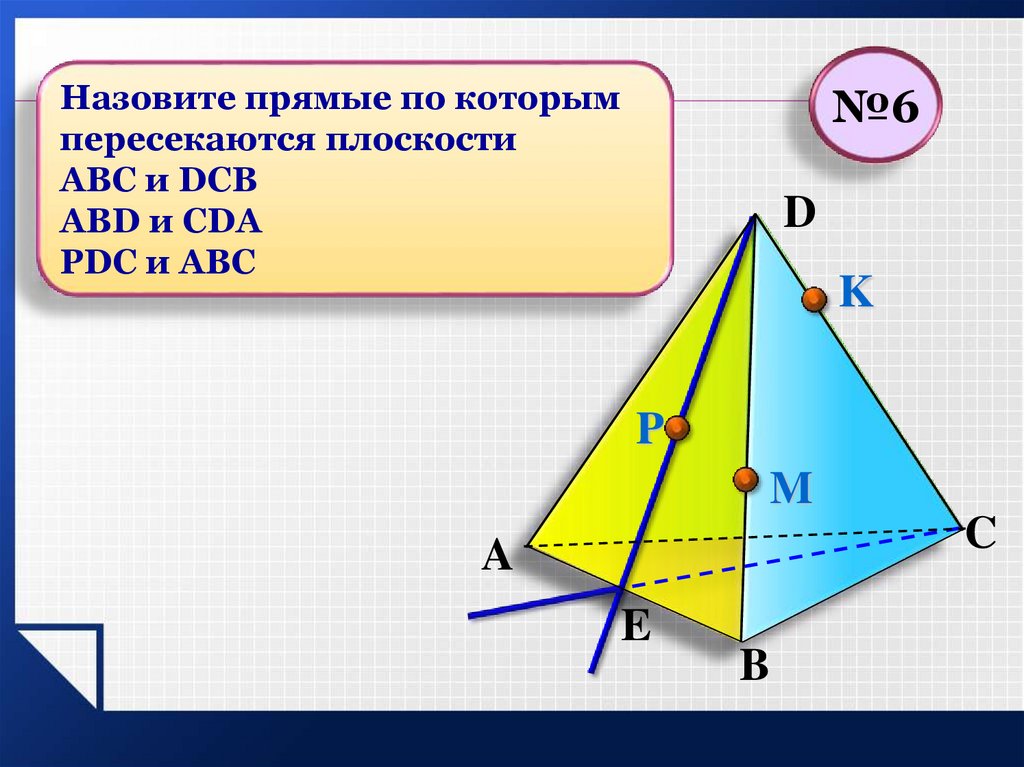
20.

Назовите прямые по которым
пересекаются плоскости
АВС и DCB
ABD и CDA
PDC и ABC
№6
D
K
P
M
C
A
E
B

21.

Назовите точки, пересечения
прямой МК с плоскостью АВD
B1
№7
Q
P
A1
C1
D1
M
K
B
A
C
D
R

22.

Назовите точки, пересечения
прямых DK и ВС с плоскостью А1В1С1
B1
№8
Q
C1
P
A1
D1
K
M
R
B
A
C
D

23.

Назовите прямую, по которой
пересекаются плоскости АА1В1 и АСD
B1
Q
P
A1
№9
C1
D1
M
K
R
B
A
C
D

24.

Назовите прямую, по которой
пересекаются плоскости PВ1C1 и ABC
B1
Q
P
A1
№10
C1
D1
M
K
R
B
A
C
D

25.

№11
Назовите точки пересечения прямых
B1
МК и DC,
В1С1 и ВР
С1М и DC
Q
P
A1
C1
D1
M
K
R
B
A
C
D

26.

П. 1;
вопросы 1 – 3 (стр. 10)
№1, №2, № 3 (стр. 10)
Повторить: аксиомы
планиметрии