Площадь параллелограмма

1.

Площадь параллелограмма

2.

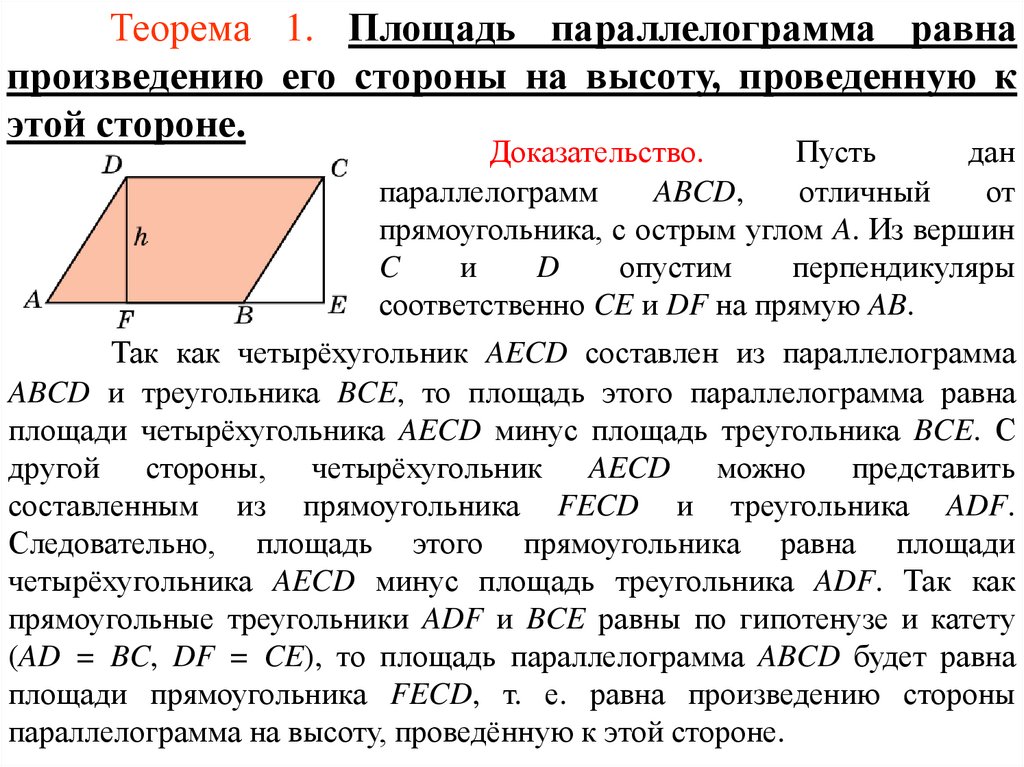
Теорема 1. Площадь параллелограмма равна
произведению его стороны на высоту, проведенную к
этой стороне.
Доказательство.
Пусть
дан
параллелограмм
ABCD,
отличный
от
прямоугольника, с острым углом A. Из вершин
C
и
D
опустим
перпендикуляры
соответственно CE и DF на прямую AB.
Так как четырёхугольник AECD составлен из параллелограмма
ABCD и треугольника BCE, то площадь этого параллелограмма равна
площади четырёхугольника AECD минус площадь треугольника BCE. С
другой стороны, четырёхугольник AECD можно представить
составленным из прямоугольника FECD и треугольника ADF.
Следовательно, площадь этого прямоугольника равна площади
четырёхугольника AECD минус площадь треугольника ADF. Так как
прямоугольные треугольники ADF и BCE равны по гипотенузе и катету
(AD = BC, DF = CE), то площадь параллелограмма ABCD будет равна
площади прямоугольника FECD, т. е. равна произведению стороны
параллелограмма на высоту, проведённую к этой стороне.

3.

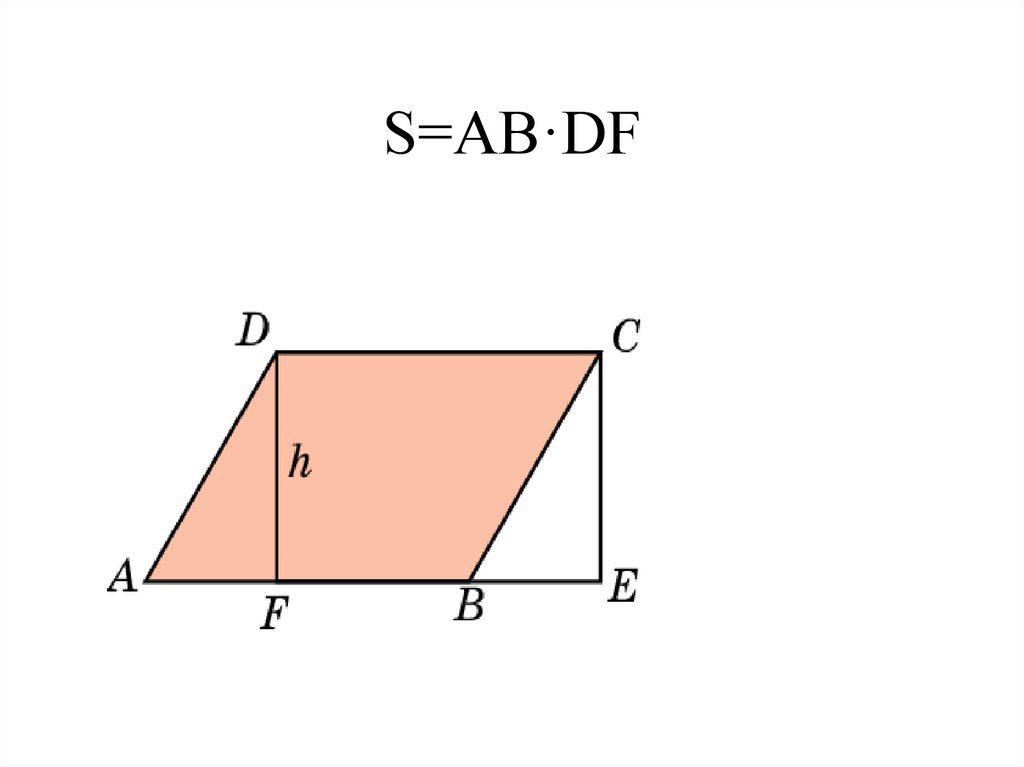
S=AB·DF

4.

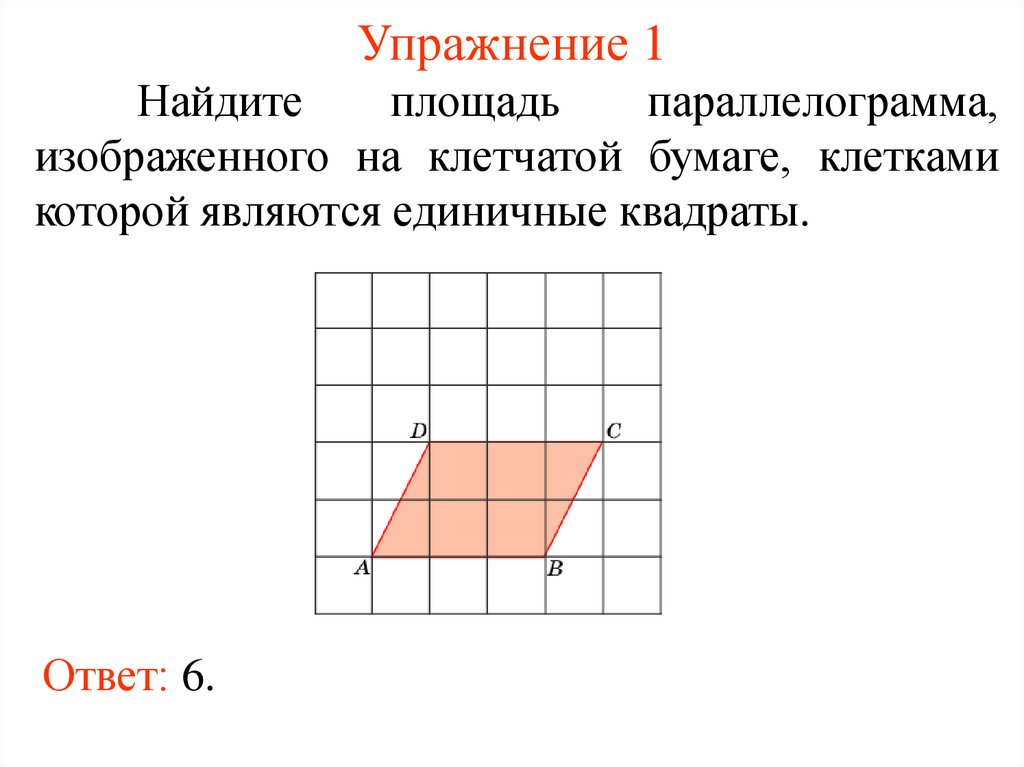
Упражнение 1
Найдите
площадь
параллелограмма,
изображенного на клетчатой бумаге, клетками
которой являются единичные квадраты.
Ответ: 6.